Analyzing Pharmaceutical Compounds through Neutrosophic Over Soft Hyperconnected Spaces

Introduction

 Uncertainty influences many facets of daily life, from the randomness of rolling dice to the unpredictability of flipping a coin on an uneven surface. These scenarios illustrate the fundamental nature of uncertainty, prompting the development of mathematical frameworks to address such variability.

In 1965, Zadeh ²⁴ introduced fuzzy sets, marking a significant milestone in mathematical theory by presenting the concept of membership degrees to model uncertainty. Zadeh also laid the groundwork for possibility theory ²⁵, broadening the scope of how uncertainties could be conceptualized and managed. Building upon Zadeh’s contributions, Bellman et al.⁴ explored decision-making under uncertainty, further solidifying the practical implications of fuzzy logic.

By introducing intuitionistic fuzzy sets, Atanassov ² provided a more comprehensive framework for representing uncertain information. These sets consider degrees of membership, non-membership, and hesitation, extending fuzzy set theory to capture uncertainty more effectively.

The introduction of neutrosophic sets by Smarandache ²⁰ represented another leap forward, introducing a novel approach to handling uncertainty that goes beyond traditional fuzzy and intuitionistic models. Neutrosophic sets allow for the representation of indeterminate, contradictory, and uncertain information, offering versatile applications across diverse fields.

Christianto [6] proposed various utilities for neutrosophic sets, highlighting their potential in modeling complex and ambiguous information scenarios. Meanwhile, Molodtsov¹⁶ introduced soft sets in 1999, which provide a mechanism to handle uncertainties in a set-theoretic context. Maji et al.¹⁵ subsequently advanced soft set theory, demonstrating its effectiveness in practical applications.

The concept of neutrosophic soft sets, introduced by Broumi⁵ in 2002, combines the flexibility of neutrosophic sets with the simplicity of soft sets, enhancing their applicability in decision-making and problem-solving.

Smarandache introduced Neutrosophic Overset, Neutrosophic Underset, and Neutrosophic Offset in the year 2016 ²⁰ Smarandache’s innovative contributions continued with the introduction of plithogenic sets and logic in 2017 ²², offering new insights into handling uncertainties involving contradictory or paradoxical information. This concept has since garnered significant attention and further exploration ²³. ⁹ RN Devi and Y Parthiban introduced a novel concept of Neutrosophic Pythagorean Plithogenic Hypersoft Set Approach to School Selection With TOPSIS Method stimulating research efforts into its theoretical underpinnings and practical implications^{7,8,17,13,14,18}.

A notable advancement in this field is the elucidation of Plithogenic Hypersoft Sets within a Fuzzy Neutrosophic Environment by Rayees et al.³, underscoring the continued evolution and integration of these theories to address complex real-world problems^1,11,12.

This manuscript clearly expain the basic definitions for neutrosophic set and topological space. By inovating a concept neutrosophic over soft semi-j open set and neutrosophic over soft hyperconnected space. An numerical illustration is given to determine the most effective one for a new pharmaceutical application using neutrosophic over soft measure of correlation.

Preliminaries

 This section introduces the basic definitions of Neutrosophic Set (NS)²⁰, Neutrosophic Over Soft Topological Space, Neutrosophic Over Set (NOS)²¹, and Neutrosophic Over Soft Set ( N_s^o-set).

Definition 1 ⁸An N_s^o-set is defined as a valued function from the set of parameters E on a non-empty set H. This is expressed as

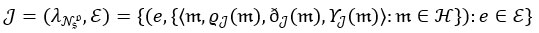
The set-valued function defining the N_s^o-set is given by

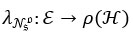
where ρ(H) represents the set of all N_s^o-set on H.

Definition 2 ⁸ An N_s^o-set ⊙={e,{〈m,0,0,Ω〉:m∈H}:e∈E} is referred to as a Null N_s^o-set, and ⊛={e,{〈m,Ω,Ω,0〉:m∈H}:e∈E} is referred to as a universal N_s^o-set .

Definition 3 ⁸ Let τ_Ns^o be a N_s^o topology in the N_s^o -set , which is a collection of subsets of an non-empty set H. The pair (H,τ_Ns^o) is called an N_s^o  topological space if it satify the following conditions:

⊙, ⊛∈τ_Ns^o

Any arbitrary collection of sets in τ_Ns^o has a union that is also contained in τ_Ns^o.

A finite intersection of sets in τ_Ns^o belongs to τ_Ns^o.

In this context, an element of τ_Ns^o is referred to as an N_s^o open set and compliment of a set τ_Ns^o  is referred to as an N_s^o  closed set.

Definition 4 ⁸ The operators for the N_s^o  topological interior and closure are defined as int_Ns^o(R) and cl_Ns^o(R), respectively for all R∈ (H,τ_Ns^o).

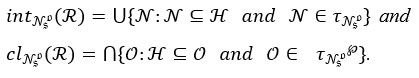
Neutrosophic Over Soft j-Open Set and Neutrosophic Over Soft Hyperconnected Space

 In this part an introduction for N_s^o β open set, N_s^o Connected Space, N_s^o  Hyperconnected Space and N_s^o  Extremely Disconnected. Additionally, some of its fundamental properties are examined.

Definition 5 An N_s^o -set J in H,τ_Ns^o  . Then J is said to be N_s^o β open set( N_s^o – β  open set) of X if and only if J ⊆ cl_Ns^o (int_Ns^o (cl_Ns^o(J)))

Theorem 3.1 Let J_α,  where α=1,2,3… be a collection of N_s^o β– open set in (H,τ_Ns^o) . Then ⋃J_α is also N_s^o β – open set in (H,τ_Ns^o).

Theorem 3.2 Let J_α,  where α=1,2,3… be a collection of N_s^o β– open set in (H,τ_Ns^o) . Then ⋃J_α is also N_s^o β – open set in (H,τ_Ns^o). .

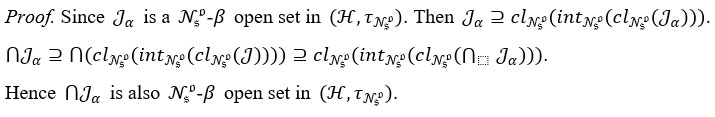
Theorem 3.3 In the space (H,τ_Ns^o) ,  every N_s^o β– open set is a neutrosophic open set.

Theorem 3.4 Let J be a N_s^o β- open set in an N_s^o-topological space (H,τ_Ns^o), and suppose J ⊆ W ⊆ clcl_Ns^o (J). Then, in (H,τ_Ns^o), Q is also a N_s^o β– open set.

Definition 6 A N_s^o in (H,τ_Ns^o)  is said to be proper, if it is neither ⊛ nor ⊙.

Definition 7 A N_s^o-topological space said to be N_s^o-connected, if it has no proper N_s^o-clopen set. N_s^o-topological space is not a N_s^o-connected then it is disconnected.

Theorem 3.5 A N_s^o -topological space said to be N_s^o-connected if and only if it doesn’t have any N_s^o-open sets J and W providing that ϱ_J (m) = Υ_W (m), Y_J (m) = ϱ_W (m)  and ð_J (m) = ð_W (m).

Theorem 3.6 A N_s^o-topological space said to be N_s^o-connected if and only if it doesn’t have any N_s^o-open sets J and W providing that ϱ_J (m) = Υ_W℘ (m) ,   Y_J (m) = ϱ_W℘ (m) and ð_J (m) = ð_W℘ (m).

Proof. Directly derived from Theorem 3.5, the proof follows.

Definition 8 An N_s^o-set J in (H,τ_Ns^o) is called

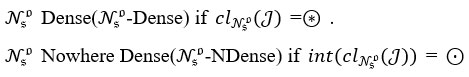
Definition 9 An N_s^o hyperconnected space is defined as an N_s^o-topological space (H,τ_Ns^o), in  which every non empty N_s^o -open subset of (H,τ_Ns^o) is N_s^o -dense in (H,τ_Ns^o).

Example 1 Let E = {e} be a set of parameter on H, where H = {s₁,s₂} with τ_Ns^o = {⊙,⊛,P₁,P₂,P₃}.

Here every non empty N_s^o-open sets ⊛,P₁,P₂,P₃ are N_s^o-Dense in H that is

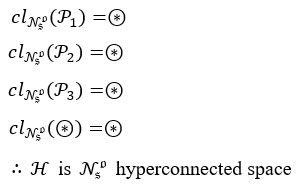
Theorem 3.7 Let (H,τ_Ns^o) be an N_s^o-topological space. Then the following properties are equivalent.

Let (H,τ_Ns^o) is N_s^o-hyperconnected. If J is a N_s^o– open set, then by the definition J = int_Ns^o (cl_Ns^o(P)).

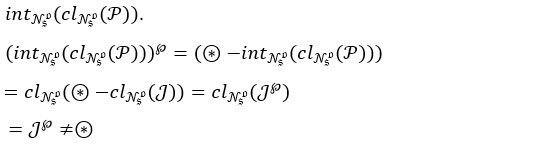
Since J^℘ ≠ ⊙ . This contradicts the assumption.

Therefore, the only N_s^o– open sets are ⊙ and ⊛.

(ii) → (i)

Let ⊙ and ⊛ be the only N_s^o-open sets in (H,τ_Ns^o).

Suppose (H,τ_Ns^o) is not an N_s^o-hyperconnected space. Then there exist a non empty J is a N_s^o-open set such that

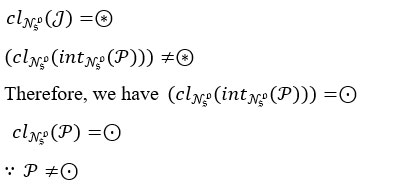
This contradicts our assumption that (H,τ_Ns^o) is not an N_s^o-hyperconnected space.

 Therefore, (H,τ_Ns^o) must be an N_s^o-hyperconnected space.

Theorem 3.8 An N_s^o-topological space (H,τ_Ns^o)  is an N_s^o-hyperconnected space if and only if every N_s^o subset is either N_s^o-Dense or N_s^o-NDense.

Proof. Let (H,τ_Ns^o) is N_s^o-hyperconnected space and let J be any N_s^o subset then J⊆⊛.

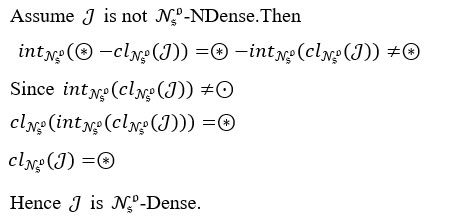
Conversely, Let J be any non empty set in N_s^o-open set. Then

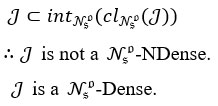
Definition 10 A N_s^o-topological space (H,τ_Ns^o) is called as N_s^o extremely disconnected(N_s^o-extremely disconnected) if the N_s^o-closure of each N_s^o-open set is N_s^o-open in (H,τ_Ns^o).

Theorem 3.9 Every N_s^o-hyperconnected space is an N_s^o-extremely disconnected, in an N_s^o-topological space (H,τ_Ns^o).

Proof. Let us take (H,τ_Ns^o) is not N_s^o-hyperconnected. be N_s^o -hyperconnected. Then for any N_s^o-open set P, cl_Ns^o(P) =⊛.

cl_Ns^o(P)  is N_s^o-open. Therefore (H,τ_Ns^o) is not N_s^o-hyperconnected. is N_s^o -extremely disconnected.

Remark 1 The following example illustrates that the converse of the above theorem does not necessarily hold true.

Example 2 Let E = {e} be a set of parameter on H, where H={s} with τ_Ns^o ={⊙,⊛,P₁,P₂,P₃}.

Correlation Measure for Neutrosophic Over Soft Set

Definition 11 ⁸Let  and  be a -set over an non-empty set , where they are defined as follows:

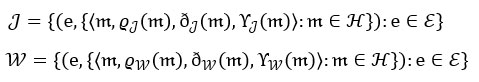
 The correlation coefficients ℵ_s and Ÿ between  and  are defined as:

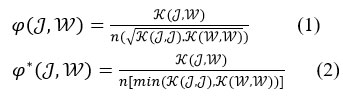
where

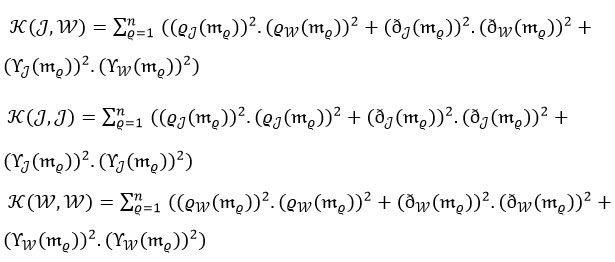
Flow Chart For Correlation Measure With To Solving _Ns^o-set

Chart 1: Flow Chart For Correlation Measure With To Solving Nso-set Click here to View Chart

Numerical Illustration

Problem Statement

A research committee is evaluating three chemical compounds to determine the most effective one for a new pharmaceutical application. The evaluation is based on multiple criteria including Efficacy, Stability, and Safety. The compounds being evaluated are Ibuprofen, Paracetamol (Acetaminophen) and Aspirin (Acetylsalicylic acid). The committee needs to rank these compounds to decide which one to prioritize for further development.

Replacement and Criteria

We consider three compounds: Ibuprofen(I), Paracetamol(P) and Aspirin(A) .

Where, molecular structure and formula for the compounds (Source: Adapted from [19])

Figure 1: Scheme of syntesis of ibuprofen Click here to View Figure

Figure 2: Scheme of syntesis of Paracetamol Click here to View Figure

Figure 3: Scheme of syntesis of aspirin Click here to View Figure

The required qualities are categorized under three main criteria: Efficacy, Stability, and Safety. The goal is to rank these compounds from best to worst based on their overall performance as Best Compound, Second Best Compound and Worst Compound.

Therefore, the Replacement sets are Compounds, Rank and the Criteria set is Efficacy, Stability, Safety.

 Analized Data

Table  1: Correlation Between Required Compounds and Essential Qualities

X	Efficacy	Stability	Safety
I	(1.3,1.1,0.5)	(0.8,1.5,0.6)	(1.4,0.8,0.8)
P	(1.2,0.7,0.9)	(1.6,0.7,0.6)	(1.4,0.6,0.3)
A	(1.8,0.7,0.6)	(1.5,0.3,0.8)	(1.6,0.9,0.4)

Table 2: Correlation between Required Qualities and Rank

Z	Best Compound	Second Best Compoun	Worst Compound
Efficacy	(0.9,1.5,0.4)	(0.5,1.3,0.6)	(1.5,0.5,0.6)
Stability	(1.1,0.5,0.3)	(1.5,0.6,0.7)	(1.4,0.3,0.7)
Safety	(1.3,0.7,0.8)	(1.1,0.7,0.4)	(0.9,0.8,0.6)

Table  3:  Correlation between Compounds and Rank

Z	Best Compound	Second Best Compoun	Worst Compound
I	0.2529	0.2118	0.2161
P	0.2767	0.3032	0.2961
A	0.2385	0.2420	0.3155

Figure 4: ℵs Correlation between Compounds and Rank Click here to View Figure

Table  4: Ÿ Correlation between Compounds and Rank

φ	Best Compound	Second Best Compound	Worst Compound
I	0.2947	0.2537	0.2547
P	0.3138	0.3535	0.3300
A	0.3527	0.3678	0.4719

 

Figure 5: Ÿ Correlation between Compounds and Rank Click here to View Figure

Table 5: Summery

Compounds	Rank
I	Best Compound
P	Second Best Compound
A	Worst Compound

 Thus the compund I got the most effective one for a new pharmaceutical application.Also, Compound P and A got second best and worst rank.

Discussion

The results indicate that Ibuprofen is the most effective compound based on the criteria evaluated, followed by Paracetamol and Aspirin. This ranking aligns with existing literature on the efficacy and safety profiles of these compounds.

Conclution

 This paper gives a clear explaination for neutrosophic over soft semi-j open set and neutrosophic over soft hyperconnected space with its basic definitions theorem and suitable example.numerical illustration is given to understand the neutrosophic over soft set concept in a easyway. The application of ℵ_s and Ÿ correlations provides a robust framework for evaluating pharmaceutical compounds. This method can be extended to other compounds and criteria, offering a versatile tool for pharmaceutical research.

Acknowledgment

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Conflict of Interest

The authors declare no conflict of interest.

References

1. Ali, M.I., Feng, F., Liu, X., Min, W.K., and Shabir, M. On some new operations in soft set theory. Computers & Mathematics with Applications, 2009, 57(9), 1547-1553.
   CrossRef
2. Atanassov, K.T. On intuitionistic fuzzy sets theory. Springer, 2012, 283.
   CrossRef
3. Ahmad, M.R., Saeed, M., Afzal, U., and Yang, M.S. A novel MCDM method based on plithogenic hypersoft sets under fuzzy neutrosophic environment. Symmetry, 2020, 12(11), 1855.
   CrossRef
4. Bellman, R.E., and Zadeh, L.A. Decision-making in a fuzzy environment. Management Science, 1970, 17(4), B-141.
   CrossRef
5. Broumi, S. Generalized neutrosophic soft set. Infinite Study, 2013.
   CrossRef
6. Christianto, V., Boyd, R.N., and Smarandache, F. Three possible applications of neutrosophic logic in fundamental and applied sciences. Infinite Study, 2020.
7. Devi, R.N., and Parthiban, Y. Decision making process over neutrosophic pythagorean soft sets using measure of correlation. Southeast Europe Journal of Soft Computing, 2023, 12(2), 06-09.
8. Devi, R.N., and Parthiban, Y. Decision making by neutrosophic over soft topological space. Neutrosophic Sets and Systems, 2024, 66, 76-94.
9. Devi, R.N., and Parthiban, Y. Enhancing decision-making for parents: A neutrosophic pythagorean plithogenic hypersoft set approach to school selection with TOPSIS method. Multi-Criteria Decision Making Models and Techniques: Neutrosophic Approaches, 2024, IGI Global, 01-20.
   CrossRef
10. Devi, R.N., and Parthiban, Y. Exploring neutrosophic over supra exterior modal topological structure: Theory and application in healthcare decision-making. Neutrosophic Sets and Systems, 2024, 72, 272-285.
11. Feng, Q., and Guo, X. A novel approach to fuzzy soft set-based group decision-making. Complexity, 2018.
    CrossRef
12. Kumaravel, S.K., Murugesan, R., Nagaram, N.B., Rasappan, S., and Yamini, G. Applications of fuzzy cognitive maps and neutrosophic cognitive maps on analysis of dengue fever. Fuzzy Logic Applications in Computer Science and Mathematics, 2023, 249-265.
    CrossRef
13. Martin, N., and Smarandache, F. Introduction to combined plithogenic hypersoft sets. Infinite Study, 2020.
14. Martin, N., Smarandache, F., and Broumi, S. Covid-19 decision-making model using extended plithogenic hypersoft sets with dual dominant attributes. International Journal of Neutrosophic Science, 2021, 13(2), 75-86.
15. Maji, P.K., Biswas, R., and Roy, A.R. Soft set theory. Computers & Mathematics with Applications, 2003, 45(4-5), 555-562.
    CrossRef
16. Molodtsov, D. Soft set theory?first results. Computers & Mathematics with Applications, 1999, 37(4-5), 19-31.
    CrossRef
17. Murugesan, R., Parthiban, Y., Devi, R., Mohan, K.R., and Kumaravel, S.K. A comparative study of fuzzy cognitive maps and neutrosophic cognitive maps on covid variants. Neutrosophic Sets and Systems, 2023, 55(1), 20.
    CrossRef
18. Sankar, C., Sujatha, R., and Nagarajan, D. Topsis by using plithogenic set in COVID-19 decision making. Infinite Study, 2020.
19. Santarupa, T. Revisiting Aspirin, Paracetamol and Ibuprofen: Discovery of Synthetic Procedures and Mode of Actions. Trends Tech Sci Res, 2020, 4(3), 37-40.
20. Smarandache, F., and Pramanik, S. New trends in neutrosophic theory and applications. Infinite Study, 2016, 1.
21. Smarandache, F. Neutrosophic overset, neutrosophic underset, and neutrosophic offset. Similarly for neutrosophic over-/under-/off-logic, probability, and statistics. Infinite Study, 2016.
    CrossRef
22. Smarandache, F. Plithogeny, plithogenic set, logic, probability, and statistics. Infinite Study, 2017.
23. Smarandache, F. Plithogenic set, an extension of crisp, fuzzy, intuitionistic fuzzy, and neutrosophic sets-revisited. Infinite Study, 2018.
24. Zadeh, L.A. Fuzzy sets. Information and Control, 1965, 8(3), 338-353.
    CrossRef
25. Zadeh, L.A. Fuzzy sets as a basis for a theory of possibility. Fuzzy Sets and Systems, 1978, 1(1), 3-28.
    CrossRef

---

This work is licensed under a Creative Commons Attribution 4.0 International License.