A Thermoacoustical and DFT Exploration of Physio-Chemical Properties for N, N-dimethylacetamide (DMA) with Water

Introduction

Examining the relationships between molecules in organic binary mixtures. Alcohols are highly self-linked liquids that have a hydrogen bond network that is three dimensions in size¹ and can be related with any other group possessing some degree of polarity ², therefore having alcohol as one of the components is of certain relevance. Because ultrasonic velocity evaluation are extremely reactive to molecular interactions, they may offer subjective information with the kind and intensity of interaction with molecules in liquid solution^3-8.

DMA is miscible with water in all ratios and with the majority of organic solvents, such as ethers, ketones, alcohols, and so forth. The boiling point of DMA, a dipolar aprotic solvent, is 438.2 K, a dipole moment of 3.72 D, which is higher than that of water, and a medium dielectric constant of 37.78 at 298.15 K⁹. Because of its exceptional solvent power and outstanding water solubility especially for high molecular weight polymers and resins. DMA is a widely used solvent in the manufacturing of synthetic fibers and polyurethanes. It functions well as a catalyst and a result for a variety of processes. In addition, it works well as an oil and gas extraction agent and plasticizer for cosmetics and pharmaceutical intermediates.

The experimental basis for selecting the suitable solvents for specific applications is provided by the estimation of  ultrasonic velocity, density,  refrective index, viscosity and their fluctuation with various proportion composition of liquid and temperature and composition ^10-20. Thus, analysis of molecular association in system of water and N, N-dimethylacetamide (DMA) has been attempted in this work. The mixture’s intermolecular interactions were examined. V_m^E , Δu, ΔR_m, L_f^E, Z^E, Δη and ΔG*^E. The linear regression polynomial equation for Curve Expert 1.3 has been fitted with these excess parameters. Using experimental data for the system, derived parameters have also been determined, including isoentropic compressibility (k_s), specific heat ratio (γ) and the effective Debye temperature (ϴ_D) at varying concentrations of DMA.

The binary mixture has also been subjected to a several rule and theories, including the Flory’s statistical theory (FST), collision factor theory (CFT), Nomoto, Vandeal and Junjie’s theories for the theoretical estimation of ultrasonic velocities. The APD (average percentage deviation) values determined from the observed values has been used to compare the comparative merits of the different mixing methods and models. Furthermore, the strength of the hydrogen bonding between molecules has been examined using density functional theory (DFT).

DFT Calculations and models

Numerous researchers^21-24 have used density functional theory to calculate molecular system properties, with remarkable understanding between experimental and theoretical results. DFT ²⁵ has been functional to compute H-bonded intermolecular interactions using Gaussian 09W^26-29 and to optimize the geometry of DMA and DMA in relation to water. The outcomes were visualized using GaussView 5.0 software³⁰.

The Natural Bond Orbital (NBO) has been utilized to quantify hyperconjugation or intermolecular delocalization³¹. The  intermolecular delocalization of the  DMA + water binary mixture has been studied by means of second-order perturbation theory using the Fock matrix in the NBO basis. The structure of DMA + water is given in Fig.1

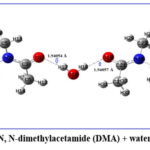Figure 1: N, N-dimethylacetamide (DMA) + water structure. Click here to View Figure

Experimental Details

Apparatus and Procedure

Ultrasonic velocity has been determined using the interferometric technique. The ultrasonic velocities were reproducible within an error margin of ±0.08%.

A pycnometer with a single capillary calibration has been used to measure densities. The graduation on the pcynometer stem was 0.01 ml. The reproducibility of the densities was within ±0.01%.

The LVDVII+Pro Brookfield viscometer has been used to measure viscosity. Brookfield Rheocalc 32 Software allows for total PC control over the instrument. The equipment has a repeatability of ±0.2% and an accuracy of ±1.0% of the full-scale range.

An accurate refractive index of ±0.001 unit was obtained with a thermostated Abbe’s refractometer, which had a range of 1.300 to 1.700 for the liquid mixtures.

Results and Discussion

Thermo dynamic parameters

Table 1 presents the experimentally measured values for DMA+ water solution with mole fraction (x₁) at varying temperatures.

Table 1: Experimentally measured parameters for the system DMA + water with x₁ of DMA at varying temperatures.

x1	u (ms-1)	ρx 10-3(kg m-3)	η(cp)	n
293.15K
0.0000 0.0999 0.1998 0.2999 0.3998 0.5000 0.6975 0.7949 0.9000 1.0000	1483.0 1768.5 1741.1 1722.8 1664.9 1639.0 1550.1 1523.8 1498.5 1472.0	0.9982 1.0000 0.9994 0.9961 0.9865 0.9739 0.9597 0.9533 0.9464 0.9398	1.002 2.930 4.634 4.918 4.072 3.340 1.840 1.475 1.219 1.012	1.333 1.379 1.405 1.419 1.427 1.431 1.435 1.436 1.436 1.437
303.15K
0.0000 0.0999 0.1998 0.2999 0.3998 0.5000 0.6975 0.7949 0.9000 1.0000	1518.0 1718.6 1702.8 1690.5 1639.7 1601.3 1521.9 1481.1 1459.0 1432.0	0.9956 0.9932 0.9924 0.9866 0.9771 0.9686 0.9511 0.9438 0.9374 0.9315	0.797 2.089 3.138 3.356 2.871 2.295 1.470 1.220 1.034 0.871	1.332 1.377 1.401 1.415 1.422 1.427 1.430 1.431 1.431 1.432
313.15K
0.0000 0.0999 0.1998 0.2999 0.3998 0.5000 0.6975 0.7949 0.9000 1.0000	1529.0 1689.7 1676.0 1658.9 1600.9 1555.2 1481.2 1448.9 1417.3 1402.0	0.9922 0.9866 0.9851 0.9776 0.9680 0.9598 0.9420 0.9352 0.9284 0.9234	0.653 1.615 2.342 2.474 2.229 1.839 1.259 1.067 0.924 0.769	1.331 1.374 1.398 1.411 1.418 1.422 1.425 1.426 1.426 1.427

For calculating isoentropic compressibility (k_s), specific heat ratio (γ) and effective Debye temperature (ϴ_D),following relations are used,

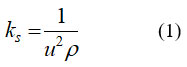
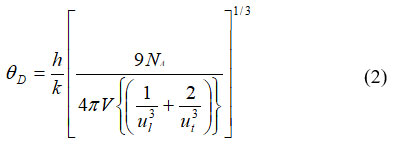
where γ, β_T and G_T are  specific heat ratio, isothermal compressibility and modulus of rigidity respectively.

It can be seen from Table 1 that at all three temperatures, ultrasonic velocity (u ) attains a maxima at .0999 mole fraction. As the concentration increases we see the ultrasonic velocity decreases. In liquid mixtures, the strength of the molecular interaction become maximum at the concentration where the velocity maxima take place. These observations agree with the earlier reported data ¹¹.

The isoentropic compressibility (k_s) reaches a least amount and then again increases with an amplify in concentration and have an opposite relationship with the velocity. The mixture under study exhibits compressibility minima in the same concentration range as the velocity maxima, as would be predicted (fig 2a). At or very close to the concentrations where complex formation takes place, a decrease in k_s and an increase in u are the results of the hydrogen bond formation strengthening the inter-molecular forces. Similar variations in ultrasonic velocity and isoentropic compressibility have also been reported earlier⁷.

The derived parameters, viz.,effective Debye temperature (ϴ_D), and  specific heat ratio (γ) provide inclusive information about the interactional and structural characteristics of the mixture at the microscopic level. It can also be seen from figures 2b and 2c that the variation of effective Debye temperature (ϴ_D) and  specific heat ratio (γ) with concentration is also non-linear, which further help the phenomenon of complex formation between dissimilar molecules ^32,33.

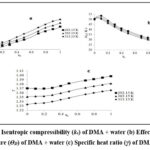Figure 2: (a) Isentropic compressibility (ks) of DMA + water (b) Effective Debye’s temperature (ϴD) of DMA + water (c) Specific heat ratio (γ) of DMA + water Click here to View Figure

Excess Parameters

Various forms of interactions between component molecules can account for the excess parameter values for binary mixtures. Non-specific van der Waal forces, dipole-dipole interactions, hydrogen bonding, donor-acceptor interactions between unlike molecules, and smaller molecules occupying the gaps left by larger molecules are a few examples of these interactions. The sign and magnitude of excess parameters are very important for figuring out how molecules in a liquid mixture interact with each other and cause molecules to move around.

Figs. 3a and 3b illustrate the deviation in ultrasonic velocity (Δu) and excess acoustic impedance (Z^E) for the system of DMA with respect to the mole fraction at varying temperatures. Analyzing the curves, it can be observed that both Δu and Z^E  have positive values. The strong specific interactions (hydrogen bonding between DMA and water) is present and the filling of smaller water molecules into the voids created by larger DMA molecues are likely responsible for the positive values of Δu and Z^E (figs. 3a and 3b). Fort and Moore ³⁴, as well as many other researchers ^16,17,35, contend that positive values of Δu and Z^E signify the presence of strong intermolecular interaction between different molecules. The high positive values like Δu and Z ^E indicates the DMA is interactive with water.

Figure 3: (a) Deviation in ultrasonic velocity (Δu) of DMA+water (b) Excess acoustic impedance (ZE) of DMA+water (c) Excess intermolecular free length (LfE) of DMA+water. Click here to View Figure

Figs 3c, 3d, and 3e demonstrate that the values of excess parameters like L_f, V_m^E and ΔR_m are all negative at all three temperatures. The hydrogen bonds with water is thought to be the reason behind DMA’s ability to take protons. The molecules in the mixture varying sizes could possibly be the cause of the reported negative values. The molar volumes of DMA and water at 298.15 K are 92.9 cc /mol and 18.06 cc/mol respectively. The larger difference in molar volume between DMA and water would result in contraction in volume due to the component molecules need to fit with other structures. The difference in component molecules sizes was also taken into account by Ali and Nain³⁶ and Pikkarainen ¹⁰ to explain the negative values of V_m^E in binary mixtures of DMA + ethanol and DMA + methanol/ethanol/propanol, respectively.

The development of strong hydrogen bonds between DMA and water molecules is further supported by the positive values of deviation in viscosity (∆η) and excess free energy of activation for viscous flow (∆G*^E) for the DMA + water system (figs 3f and 3g). The values of ∆η and ∆G*^E extrema decreasewith elevation in temperature, indicating that the interaction between molecules is temperature sensitive and weakens as temperature rises. Similar patterns in ∆η and ∆G*^E  have also been observed in the cases of DMA + methanol ^5,10 and water + sulfonane³⁷. Table 2 provides the standard deviation  (σ(Y^E)) and coefficient a_i as determined by the curve expert 1.3 software.

Table 2:  a_i for excess parameters and their σ(Y^E) for binary system at three temperatures

Functions	a1	a2		a3	a4		a5	σ(YE)
DMA + Water
T=293.15 K
VmEx106 (m3mol-1)	0.0439	-8.5174		13.8936	-7.0029		1.5601	0.0961
Δη(cp)	-0.1577	33.6014		-93.8688	87.5647		-27.0823	0.2677
ΔRm	-0.1243	-66.2275		179.5525	-183.0507		69.9332	0.2055
ΔG*E(kJmol-1)	0.0263	38.9811		-107.9595	106.4839		-37.5455	0.0719
Δu(ms-1)	21.8986	3044.8484		-11094.579	13804.9984		-5786.9105	36.0507
ZE(kgm-2s-1)	0.1963	33.4995		-122.1126	151.5864		-63.2677	0.3212
LfE(A0)	-0.0049	-0.7438		2.6412	-3.2391		1.3488	0.0081
T=303.15 K
VmEx106 (m3mol-1)	0.0257	-6.9623		6.1435	5.2908		-4.5181	0.0450
Δη(cp)	-0.0967	21.9662		-62.3313	60.0138		-19.5212	0.1635
ΔRm	-1.2300	-65.3446		175.8656	-177.8814		67.5653	0.2053
ΔG*E(kJmol-1)	0.0158	35.8636		-101.4766	103.3124		-37.7320	0.0336
Δu(ms-1)	13.8508	2290.4042		-8014.7883	9629.9490		-3925.4604	23.0465
ZE(kgm-2s-1)	0.1267	24.1115		-83.9868	99.9696		-40.2773	0.2125
LfE(A0)	-0.0033	-0.5731		1.9308	-2.2627		0.9096	0.0054
T=313.15 K
VmEx106 (m3mol-1)	0.0229	-6.5455	4.9527			7.0597	-5.4994		0.0432
Δη(cp)	-0.0554	15.3968		-42.9074	40.9669		-13.3799	0.0911
ΔRm	-0.1325	-66.2452		179.3324	-182.2330		69.3677	0.2213
ΔG*E(kJmol-1)	0.0244	33.3978		-94.6918	97.7223		-36.4664	0.0421
Δu(m.s-1)	10.1288	1994.9188		-7123.6009	8604.9702		-3493.1798	17.4459
ZE (kgm-2s-1)	0.0887	20.5102		-73.1977	87.7487		-35.2135	0.1553
LfE(A0)	-0.0024	-0.5116		1.7424	-2.0321		0.8054	0.0042

 

The values of the APD (Average percentage deviation) of ultrasonic velocity (u) anticipated by different semi-empirical rules are shown in Table 3. It shows that the CFT relation gives the minimum APD and Vandeal’s relation gives the maximum APD for this system. However, the APD values predicted by Nomoto, Jungie, and FST are nearly equal.

Table 3: APD of several theories utilized for determination of u.

Temperatures	CFT	FST	Nomoto	Vandeal	Junjie
DMA+Water
293.15K	5.8192	9.5936	7.7528	21.1827	7.7760
303.15K	4.3209	7.3986	7.2443	19.1958	7.3438
313.15K	3.1629	5.1687	6.6258	17.8053	6.7998

 

Theoretical study

Natural bond orbital (NBO) study

NBO examination relies on technique that provide a collection of algorithms that make it possible to extract the basic bonding concept through DFT calculations³¹. NBO study is an crucial tool for evaluating the molecular interaction in molecules, in addition to given that a useful establishment for analyzing conjugative interaction or charge transfer in molecular systems. Strong electrostatic hyperconjugative interactions are revealed by the NBO study³⁸. The NBO study of  DMA has been already mentioned in published work²⁴ and for DMA + water the interaction energy of LP1(N2) with anti-bonding π^*(O1-C3) increases to 67.47 kcal/mol showing higher stabilization of the system. The interaction of LP(2) of O1 and O19 with s*(O16-H17) and s*(O16-H18) respectively results in similar stabilization energy of 5.45 kcal/mol.

DFT investigation of H-bonded intermolecular interaction

To compute the intermolecular hydrogen bonding strength using Bader’s Atoms in Molecules (AIM) hypothesis³⁹ has been mentioned in published work²⁴. In this work to determined the hydrogen bond strength for the DMA and water binary mixture. It was computed to be 5.79825 kcal/moland 5.78869 kcal/mol at B3LYP corresponding to two hydrogen bonds formed between water and DMA molecules. Table 4 lists the topological parameters.

Table 4: Topological parameters for DMA+water

Parameters	O19—H18	O1—H17
Electron density (ρBCP) a.u.	0.02481	0.02481
Laplacian of electron density a.u.	0.09056	0.09507
Lagrangian kinetic energy G(r) a.u.	0.02055	0.02055
Hamiltonian kinetic energy K(r) a.u.	-0.00209	-0.00209
Potential energy density V(r) a.u.	-0.01846	-0.01845
Eigen value λ1	-0.01846	-0.01845
Eigen value λ2	-0.03252	-0.03252
Eigen value λ3	0.15679	0.15680
H-Bond energy (kcal/mol)	5.79825	5.78869

 

To depict the distribution of electron densities, electron localised field (ELF) graph has been constructed, as shown in fig. 4. The overlapping of the blue zone in Fig. 4 depicts interaction with the oxygen atom of DMA molecules and the H atoms of water molecules in the binary mixture. The figure provides sufficient theoretical support for such intermolecular bonds between DMA and water.

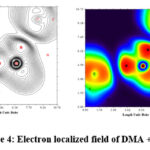Figure 4: Electron localized field of DMA + water. Click here to View Figure

HOMO and LUMO (fig 5) plots have been drawn using the optimized structure. HOMO has been distributed over water and DMA molecules, while LUMO is confined to DMA molecules.

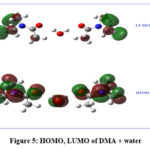Figure 5: HOMO, LUMO of DMA + water. Click here to View Figure

The total density of states (TDOS) and partial density of states (PDOS) plots seen in Fig. 6 were plotted using the Gauss-Sum 2.2 Program⁴⁰. Although the PDOS plot shows a group’s relative contributions towards each molecular orbital, the TDOS plot showing population assessment per orbital provides the allocation of molecular orbitals under a certain spectral region.

Figure 6: TDOS and PDOS plotsof DMA + water. Click here to View Figure

Conclusions

The excess parameters were calculated from experimentally measured u, ρ, η and n at varying temperatures. The presence of strong interactions in DMA + water systems is indicated by the observed negative values of L_f^E, Vm^E, ΔR_m and positive values of ∆u, Z^E, ∆η and ΔG^*E . The applicability of semi-empirical relations and theories is demonstrated by comparing the average percentage deviation of estimated and experimental values of ultrasonic velocity. Excellent agreement between experimental and theoretical values can be seen in the root mean square deviations for density prediction derived from the density models. The DFT/B3LYP method’s computed data was used to confirm all of the experimental results.

Acknowledgment

One of the authors (Laxmi Kumari) gratefully acknowledges to the UGC, New Delhi and Government of India for providing financial support under BSR fellowship (F-25-1/2014-15 (BSR)/7-177/2007/(BSR) dated 7^th October, 2015 during the research.

Conflicts of Interests

The authors declare no competing interests.

References

1. Kumari, L.; Gupta, S.; Singh, I.; Prasad, O.; Sinha, L.; Gupta, M.; Thermodynamic, spectroscopic and DFT studies of binary mixtures of poly(vinylpyrrolidone) (PVP) with ethanol, 1-propanol and 1-butanol. J. Mol. Liq. 2020, 299, 1-13.
   CrossRef
2. Yasmin, M.; Gupta, M.;  Shukla, J. P.; Acoustical study of molecular interactions in polymer solutions through various thermodynamical parameters and flory’s theory at 298.15 K. Phy. Chem. Liq. 2010, 48, 682-697.
   CrossRef
3. Nain, A. K.; Densities, ultrasonic speeds, viscosities and excess properties of binary mixtures of methyl methacrylate with N, N–dimethylformamide and N, N–dimethylacetamide at different temperatures. J. Chem. Thermodyn. 2013, 60, 105-116.
   CrossRef
4. Kumari, L.; Sinha, L.; Prasad, O.; Gupta, M.; Study of molecular association in binary mixtures of poly(vinyl pyrrolidone) (PVP) with ethanol, 1-propanol and 1-butanol through thermo-acoustical, FT-IR, UV–Vis spectroscopy and DFT studies. Eur. Phys. J. D. 2021, 75, 1-11.
   CrossRef
5. Mrad, S.; Lafuente, C.; Hichri, M.; Khattech, I.; Density, Speed of sound, refractive index, and viscosity of the binary mixtures of N, N‑dimethylacetamide with methanol and ethanol. J. Chem. Eng. Data 2016, 61, 2946−2953.
   CrossRef
6. Vibhu, I.; Singh, A. K.; Gupta, M.; Shukla, J. P.; Ultrasonic and IR investigation of N–H-N complexes in ternary mixtures. J. Mol. Liq. 2004, 115, 1-3.
   CrossRef
7. Gupta, M.; Shukla J. P.; Ultrasonic investigation of molecular association in binary mixtures-Dioxan+formic acid, salicylic acid and benzoic acid. Indian J. Pure Appl. Phys. 1996, 34, 769-772.
8. Singh, S.; Vibhu, I.; Gupta, M.; Shukla, J. P.; Excess acoustical and volumetric properties and the theoretical estimation of the excess thermodynamic functions of binary liquid mixtures. Chin. J. Phys. 2007, 45, 412-424.
9. Marcus, Y.; Introduction to liquid state chemistry. Wiley Interscience 1977.
10. Pikkarainen, L.; Densities and viscosities of binary mixtures of N, N–Dimethylacetamide with aliphatic alcohols. J. Chem. Eng. Data 1903, 28, 344-347.
    CrossRef
11. Kazimierczuk, M. J.; Szydlowski, J.; Physicochemical properties of solutions of amides in H₂O and in D₂O. J. Solut. Chem. 2001, 30, 623-640.
    CrossRef
12. Shukla, D.; Singh, S.; Parveen, S.; Gupta, M.; Shukla, J. P.; A corresponding state model for the prediction of the viscosity of pure liquids and liquid mixtures. J. Mol. Liq. 2007, 136, 111-116.
    CrossRef
13. Rastogi, M.; Awasthi, A.; Gupta, M.; Shukla, J. P.; Molecular association of aliphatic ketones and phenol in a nonpolar solvent-ultrasonic and IR study. J. Mol. Liq. 2003, 107, 185-204.
    CrossRef
14. Das, D.; Messaâdi, A.; Barhoumi, Z.; Ouerfelli, N.; The Relative reduced redlich-kister equations for correlating excess properties of N, N-dimethylacetamide+water binary mixtures at temperatures from 298.15 K to 318.15 K. J. Sol. Chem. 2012, 41, 1555-1574.
    CrossRef
15. Villca, G.; Justel, F. J.; Jimenez, Y. P.; Water activity, density, sound velocity, refractive index and viscosity of the {(NH₄)₆Mo₇O₂₄ + poly(ethylene glycol) + H₂O} system in the temperature range from 313.15 to 333.15 K: Experiment and modeling. J. Chem. Thermodyn. 2020, 142, 1-11.
    CrossRef
16. Singh, K. P.; Agarwal, H.; Shukla, V. K.; Vibhu, I.; Gupta, M.; Shukla, J. P.; Ultrasonic velocities, densities, and refractive indices of binary mixtures of polyethylene glycol 250 dimethyl ether with 1-propanol and with 1-butanol. J. Solut. Chem. 2010, 39, 1749-1762.
    CrossRef
17. Yasmin, M.; Gupta, M.; Thermodynamical study of alcoholic solutions of Poly (ethylene glycol) Diacrylate and Poly (ethylene glycol) Dimethacrylate. Int. J. Thermodyn. 2012, 15, 111-117.
    CrossRef
18. Shukla, D.; Singh, S.; Parveen, S.; Gupta, M.; Shukla, J. P.; Acoustical properties of binary mixtures of heptane with ethyl acetate or butyl. Chin. J. Phys. 2010, 28, 371-377.
    CrossRef
19. Mundhwa, K. M.; Alam, R.; Henni, A.; Volumetric properties, viscosities, and refractive indices for aqueous 2-((2-Aminoethyl)amino) ethanol solutions from (298.15 to 343.15). J. Chem. Eng. Data 2006, 51, 1268-1273.
    CrossRef
20. Sivakami, K. U.; Vaideeswaran, S.; Rosevenis, A.; Thermodynamic properties and interaction abilities of ternary liquid mixtures at 308.15 K. J. Environ. Nanotech. 2018, 7, 22-33.
21. Singh, I.; El-Emam, A. A.; Pathak, S. K.; Srivastava, R.; Shukla, V. K.; Prasad, O.; Sinha, L.;  Experimental and theoretical DFT (B3LYP, X3LYP, CAM-B3LYP and M06-2X) study on electronic structure, spectral features, hydrogen bonding and solvent effects of 4-methylthiadiazole-5-carboxylic acid. Mol. Simul. 2019, 45, 1029-1043.
    CrossRef
22. Sinha, L.; Prasad, O.; Chand, S.; Sachan, A. K.;  Pathak, S. K.; Shukla, V. K.; Karabacak, M.; Asiri, A. M.; FT-IR, FT-Raman and UV spectroscopic investigation, electronic properties, electric moments, and NBO analysis of anethole using quantum chemical calculations. Spectrochim. Acta A, 2014, 133, 165-177.
    CrossRef
23. Kumari, L.; Kumar, U.; Sinha L.; Prasad, O.; Yadav, B. C.; Gupta, M.; Surface modifcation and characterization of h‑BN‑doped PVP thin flm and its application as humidity sensor with theoretical DFT calculations. Chem. Pap. 2021, 75, 4055-4068.
    CrossRef
24. Agarwal, H.; Kumari, L.; Sinha, L.; Prasad, O.; Gupta, M.; Thermoacoustic and DFT Analysis of N, N‑Dimethylacetamide (DMA) with 1‑propanol and methanol at 293.15, 303.15, and 313.15 K. Braz. J. Phys. 2021, 51, 515-526.
    CrossRef
25. Kohn, W.; Sham, L. J.; Self-consistent equations including exchange and correlation effects Phys. Rev. 1965, 140, A1133-A1138.
    CrossRef
26. Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb, M. A.; Cheeseman, J. R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G. A.; et. al. Gaussian Inc. Wallingford CT. 2009.
27. Becke, A. D.; Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648-5652.
    CrossRef
28. Lee, C.; Yang, W.; Parr, R. G.; Development of the colle-salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B, 1988, 37, 785-789.
    CrossRef
29. Miehlich, B.; Savin, A.; Stoll, H.; Preuss, H.; Results obtained with the correlation energy density functionals of becke and Lee, Yang and Parr. Chem. Phys. Lett. 1988, 157, 200–206.
    CrossRef
30. Frisch, E.; Hratchian, H. P.; Dennington, R. D.; II, et al. Gaussian Inc., GaussView Version 5.0.8. Sci. 2009, 7, 1505-1517.
31. Glendening, E. D.; Landis, C. R.; Weinhold, F.; Natural bond orbital methods, WIREs Comput. Mol. Sci. 2012, 2, 1-42.
    CrossRef
32. Parveen, S.; Yasmin, M.; Gupta, M.; Shukla, J. P.; Thermoacoustical and excess properties of binary mixtures of ethyl butyrate with methanol and vinyl acetate. Int. J. Thermodyn. 2010, 13, 59-66.
33. Parveen, S.; Singh, S.; Shukla, D.; Yasmin, M.; Gupta, M.; Shukla, J. P.;  Study of molecular interactions in binary mixtures of aniline with carboxylic acids at 293.15 K, 303.15 K and 313.15 K. J. Solution Chem. 2012, 41, 156-172.
    CrossRef
34. Fort, R. J.; Moore, W. R.; Adiabatic compressibilities of binary liquid mixtures. J. Chem.   Soc. Faraday Trans. 1965, 61, 2102-2111.
    CrossRef
35. Kavitha, R.; Jayakumar, S.; Uma, R.; Ultrasonic velocity, density and viscosity of binary liquid mixtures of acetone with toluene, chlorobenzene and nitrobenzene. Int. J. Chem. Applicat. 2011, 3, 19-33.
36. Ali, A.; Nain, A. K.; Interactions in binary N, N-dimethylacetamide + ethanol and ternary lithium nitrate + N, N dimethylacetamide + ethanol mixtures. Phys. Chem. Liq. 1999, 37, 161-174.
    CrossRef
37. Aminabhavi, T. M.; Gopalakrishna, B.; Density, viscosity, refractive index, and speed of sound in aqueous mixtures of NJV-dimethylformamide, dimethyl sulfoxide, NJV-dimethylacetamide, acetonitrile, ethylene glycol, diethylene glycol, 1,4-dioxane, tetrahydrofuran, 2-methoxyethanol, and 2-ethoxyethanol at 298.15 K. J. Chem. Eng. Data 1995, 40, 856-861.
    CrossRef
38. Chand, S.; Fatmah, A. M.; Omary, A.; Emam, A. A. K.; Shukla, V. K.; Prasad, O.; Sinha, L.; Study on molecular structure, spectroscopic behavior, NBO, and NLO analysis of 3-methylbezothiazole-2-thione. Spectrochim. Acta A Mol. Biomol. Spectrosc., 2015, 146, 129–141.
    CrossRef
39. Bader, R. F. W.; A quantum theory of molecular structure and its applications. Chem. Rev. 1991, 91, 893–928.
    CrossRef
40. Boyle, N. M. O.; Tenderholt, A. L.; Langer, K. M.; Cclib: A library for package-independent computational chemistry algorithms. J. Comput. Chem. 2008, 29, 839– 845.
    CrossRef

---

This work is licensed under a Creative Commons Attribution 4.0 International License.