Utilization of Granular Activated Carbon for Sustainable Environmental Contaminants Remediation

Introduction

Water is a crucial advent for human beings and is used in many sectors. Rapid and unorganized urban and industrial developments have contributed to various environmental issues. The water resources continue to be contaminated with run-off water from agriculture fields containing pesticides, fertilizers, the industrial effluents, raising serious health and environmental concerns. The improper disposal and management of industrial and municipal wastewater are major sources of water pollution. Polluted water contains toxic metals, inorganic chemicals, and colored reagents creating a significant threat to public health.

Industries such as electroplating, leather, and textiles release substantial amounts of heavy metals, including arsenic, manganese, chromium, cobalt, lead, and nickel, contributing significantly to water pollution. Heavy metals highly reactive and non-degradable which may be deposited on the surface and water resources, posing immense dangers to all forms of life and the environment ^1,2. The excess level of manganese in the water causes  several detrimental consequences and can damage multiple organ of human³. As well as manganese deficiencies causes wide range of clinical complications, including migraines, fibromyalgia, arrhythmia⁴. Consequently, the removal of heavy metals from wastewater is a challenging task that demands continuous monitoring and attention. Heavy metals, accumulate in the environment, emphasizing the urgency of their removal from wastewater before discharge. Several treatment methods, such as chemical reduction, electro-coagulation, membrane adsorption ⁵, ion exchange^6,7, precipitation, membrane separation ⁸, and adsorption are available to lower the Mn (II) ion concentration from industrial wastewater ^9,10. To prevent future adverse consequences on both human beings and the environment, these hazardous metals must be effectively removed from wastewater. However, the effective method for the treatment of heavy metals is the adsorption technique and the specific properties of adsorbents elevate the adsorption process. The appropriate selection of adsorbents is crucial, focusing on functional groups, high surface area, porosity, and polarity of adsorbents. Adsorption has proven to be more efficient and cost-effective for heavy metal removal compared to other methods. Its fundamental advantage lies in its economic viability, making it a low-cost approach for heavy metal removal . Another significant benefit of the adsorption process is its ability to be regenerated, allowing for the repeated use of adsorbents ^11,12. Both commercial and conventional adsorbents have applications in scavenging heavy metals from aqueous phases ^13,14.

Various low cost adsorbents were used by different researcher for the removal of heavy metals from aqueous phase ^15,16. Heavy metal pollution remains a pressing concern, and adsorption offers a powerful solution. This method not only effectively remediates heavy metals from wastewater but also demonstrates a minimal environmental impact. This makes it a green technology that significantly enhances the wastewater treatment process. ^17,20. 

Material and Method

All chemicals of analytical grade were utilized. Initially, a requisite amount of MnSO₄ was dissolved in 1 liter of distilled water to prepare a stock solution of Mn²⁺ ions. Different grades of carbon were initially sized using a siever, resulting in particles ranging from 840μ to 1400μ mesh size. Subsequently, activated carbon particles F-816 and F-820 were thoroughly washed with boiled distilled water repeatedly, till a clear leachate was obtained. The washed carbon particles were collected and dried at a temperature of 100-1100 C in an oven and then stored in desiccator till further use.

3,5-Dintrobenzoic acid was chosen as the ligand and then it is recrystallized by conventional method. The purity of 3,5-Dinitrobenzoic acid an essential component of the experiment, was confirmed by determining its melting point using Thiele’s apparatus. The experimental melting point of 206˚C was in close agreement with the literature value of 207°C, indicating its purity ²¹. 

For determining adsorption isotherm, 200 ml solution containing a specific concentration of 3,5-Dinitrobenzoic acid and 0.5 gm dried granular activated carbon were taken in a shaking bottle. The mixture was shaken for 5 hours using a mechanical shaker (Remi Model, No. R.S.24). After that, the solution was filtered out, and the carbon was properly washed with distilled water multiple times. Then, 200 ml Mn²⁺ ion solution of p^H5 and washed carbon were transferred into the shaking bottle. The resulting mixture was shaken at a constant temperature of 25 ±1°C for 5 hrs. The Mn²⁺ ions concentration, both before and after adsorption, was determined in mg/L by measuring absorbances using a spectrophotometer. The experimental data were analyzed using a calibration curve, ensuring accurate quantification. The graph was drawn by using the values of absorbance and concentrations of different standard solutions of Mn^2+. To guarantee the reliability of the results, the experiments were repeatedly done to ensure consistency and reproducibility.  

Result and discussion

Figure 1a: Scanning electron Micrograph of F-816 before adsorption and 1b-after adsorption of Mn2+, System: F-816_3,5-Dinitrobenzoicacid_ Mn2+ Click here to View Figure

Figure 2a: Scanning electron micrograph of F-820 before adsorption and 2b-after adsorption of Mn2+, System: F-820_3,5-Dinitrobenzoic acid _Mn2+ Click here to View Figure

Scanning electron micrographs were taken at various magnifications, displayed in fig 1a and 2a, revealing large cracks and uneven cavities on the surface of both Granular Activated Carbon (GAC) i.e. F-816 and F-820. These irregularities provide a substantial surface area, enhancing the metal adsorption capacity for Mn²⁺ ions. Changes in the adsorbent’s surface morphology after adsorption are illustrated in Fig 1b and Fig 2b. It was noted that the previously uniform porosity of the adsorbent was disrupted due to the accumulation of Mn²⁺ ions on the carbon surface.

The Adsorption of Mn²⁺ ions on ligand-loaded GAC was investigated using batch adsorption studies.  The concentration of Mn²⁺ ions was calculated by the following equation,

where qe  = The concentration of Mn²⁺ on the ligand-loaded granular activated carbon, expressed in milligrams per millimole of ligand, the initial and equilibrium concentrations of Mn²⁺ ions i.e. Co and Ce, in milligrams per liter respectively . The variables V and W represent the volume of the solution in liters and the weight of the adsorbent in grams, respectively. The equilibrium isotherms for the ligand-loaded granular activated carbon were obtained by plotting the graph of qe (the amount of adsorbed Mn²⁺ per millimole of ligand) against Ce (the equilibrium concentration of Mn²⁺ ions). The results of these plots are illustrated in Figures 3 and 4.

Figure 3: Equilibrium Isotherm, System- F-816_3,5-Dinitrobenzoic acid_Mn2 Click here to View Figure

Figure 4: Equilibrium isotherm, System-F-820_3,5-Dinitrobenzoic acid_ Mn2+ Click here to View Figure

Langmuir, Freundlich, and Temkin models were used in an attempt to fit the equilibrium isotherm data on both systems i.e. F 816 – 3,5-Dinitrobenzoic acid+Mn²⁺ and F-820 -3,5-Dinitrobenzoic acid+Mn^2+.

In the first, the linearized form of the Langmuir equation is expressed by the following equation ²²    

The Langmuir constant, denoted as b, Q⁰ represents the amount adsorbed per unit weight of activated carbon forming a complex monolayer on the activated carbon.

The linear graphs of 1/qe verses 1/Ce in fig 5 and 7 demonstrate the applicability of the Langmuir model. All the constants i.e. the Langmuir constant b and Q⁰ were determined from the slope and intercept of the Langmuir isotherm, respectively given in Table 1.  The Langmuir equation and corresponding regression coefficients are shown in Table 2.

The second one is the Freundlich model and equation²³ is represented as

Above equation may be linearized as

Fig 6 and fig 8 show consistent linear plots of log Ce versus log qe which demonstrate    the validity of the Freundlich equation across a range of concentrations. The Freundlich constants, 1/n and Kf, were calculated from the slope and intercept of the Freundlich equation, respectively. These Freundlich constants have been reported in Table 1, and the corresponding equation along with the regression coefficients are presented in Table 2.

Third one is the Temkin model²⁴ which is represented by the following equation

The linearized form of the above equation can be expressed as

where B_T is the Temkin constant associated with the heat of adsorption (in kJ/mol), The variation of adsorption energy b ( kJ/mol), R is the Universal gas constant (8.314 J/mol•K), T is the absolute temperature (in K), and K_T is the Temkin isotherm constant (in L/mg). The Temkin isotherm posits that the heat of adsorption decreases linearly due to interactions between the adsorbent and adsorbate molecules. It provides insight into the adsorption potential of the adsorbent for the adsorbate. The Temkin constants, B_T and K_T, for Mn²⁺ ions were determined by plotting ln(Ce) against qe. The resulting linear plots over a concentration range allowed the calculation of Temkin constants, which are presented in Table 1. The R² values indicated a partial fit of the data to the Temkin adsorption isotherm for both systems: F-816-3,5-Dinitrobenzoic acid+Mn²⁺ and F-820-3,5-Dinitrobenzoic acid+Mn^2+. The adsorption equilibrium data in this study were assessed using Langmuir, Freundlich, and Temkin isotherms. Figures 5 to 10 depict the plots for the Langmuir, Freundlich, and Temkin isotherms, respectively. The correlation factor R² = 1 suggests that the Langmuir model provides a more accurate depiction of the adsorption process compared to the Freundlich and Temkin models.

Figure 5: Langmuir Adsorption Isotherm  System- F-816_3,5-Dinitrobenzoic acid_Mn2+ Click here to View Figure

Figure 6: Freundlich Adsorption Isotherm System- F-816_3,5-Dinitrobenzoic acid_Mn2+       Click here to View Figure

Figure 7: Langmuir Adsorption Isotherm System- F-816_3,5-Dinitrobenzoic acid_Mn2+ Click here to View Figure

Figure 8: Freundlich Adsorption Isotherm System-F-820_3,5-Dinitrobenzoic acid-Mn2+ Click here to View Figure

Figure 9: Temkin Adsorption Isotherm System-F-816_3,5-Dinitrobenzoic acid_Mn2+ Click here to View Figure

Figure 10: Temkin Adsorption Isotherm System-F-820_ 3,5-Dinitrobenzoic acid_Mn2+ Click here to View Figure

Kinetics studies
To investigate the adsorption kinetics of Mn²⁺ on granular activated carbon (GAC), kinetic analyses employing Lagergren’s pseudo-first-order and pseudo-second-order models were conducted. These analyses aid in understanding the rate of adsorption and identifying the rate-limiting step in the transport mechanism, essential for the design and modeling of the adsorption process.

The Lagergren pseudo-first-order model is described by the following linear equation:

ln (qe​−qt​)= ln qe​−k1​⋅t

Here, qt​ is the amount of Manganese on the ligand absorbed on GAC (mg/mmol) at any time t, qe​ is the amount of Manganese on the ligand absorbed on GAC at equilibrium (mg/mmol), and k1​ is the rate constant of the pseudo-first-order adsorption process (hrs⁻¹). The values of k1​ and qe​ are determined by plotting t versus ln(qe​−qt​). The metal uptake capacity at equilibrium and the rate constant for the pseudo-first-order model can be obtained from the slope and intercept of the plot. Table 3 presents the metal uptake capacity and rate constants for the pseudo-first-order model for different granular activated carbons. The experimental data for the F-816_3,5-Dinitrobenzoic acid_Mn²⁺ system and the F-820_3,5-Dinitrobenzoic acid_Mn²⁺ system are illustrated in fig 11 and fig 13, respectively.

The pseudo-second-order kinetics can be expressed in a linear form as follows:

Here, k2​ is the rate constant of the pseudo-second-order adsorption process. This equation allows for the determination of ​ and  by plotting  against t.

The results of the pseudo-second-order kinetics analysis provide further insights into the adsorption process i.e chemisorption and rate limiting step which contribute to a comprehensive understanding of system.

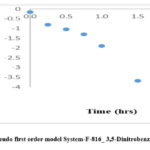Figure 11: Pseudo first order model System-F-816_ 3,5-Dinitrobenzoic acid_Mn2+ Click here to View Figure

Figure 12: Pseudo second order model System-F-816_ 3,5-Dinitrobenzoic acid_Mn2+    Click here to View Figure

Figure 13: Pseudo first order model System: F-820_ 3,5-Dinitrobenzoic acid_Mn2+ Click here to View Figure

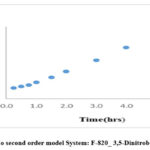Figure 14: Pseudo second order model System: F-820_ 3,5-Dinitrobenzoic acid_Mn2+ Click here to View Figure

Table 1: Constants for Langmuir, Freundlich and Temkin adsorption isotherm

S.N.	System	Langmuir constant		Freundlich Constant		Temkin    Constant		qmax(mg/m.mole
		Q0	b	1/n	Kf	BT	KT	qmax
1	GAC- F 816-3,5-Dinitrobenzoic acid+Mn2+	1.5151	0.4091	0.310	0.5956	0.331	3.9165	1.2500
2	GAC-F-820 -3,5- Dinitrobenzoic acid+Mn2+	1.5337	0.4298	0.256	0.6886	0.228	7.4627	1.2750

Table 2: Isotherm equation and regression coefficient.

S. N.	Adsorption system	Equation	Reg. Coefficient	Types of isotherms
1	GAC-F-816-3,5-Dinitrobenzoic  +Mn2+	y=1.6133x+0.6602	R² = 0.9853	Langmuir adsorption isotherm
2	GACF-820-3,5-Dinitrobenzoic acid+Mn2+	y=1.5176x+0.6526	R² = 0.9925	Langmuir adsorption isotherm
3	GAC-F-816-3,5-Dinitrobenzoic acid+Mn2+	y=0.3105x-0.2251	R= 0.9660	Freundlich adsorption  isotherm
4	GACF-820-3,5-Dinitrobenzoic acid+Mn2+	y=0.2567x-0.1623	R² = 0.9780	Freundlich adsorption  isotherm
5	GAC-F-816-3,5-Dinitrobenzoic acid+Mn2+	y=0.331+0.452	R²= 0.9610	Temkin adsorption  isotherm
6	GAC-F-820-3,5-Dinitrobenzoic acid+Mn2+	y=0.288+0.579	R² = 0.9830	Temkin adsorption  isotherm

 

Table 3: Parameters of Pseudo First Order and Second Order Kinetic Model and Regression Coefficients

S.N.	System	Pseudo First Order				Pseudo Second Order
		K1 (hrs.-1)	qe cal . mg/mmol	qe  expt mg/mmol	R2	K2	qe cal mg/mmol	qe  expt mg/mmol	R2
1	F-816_3,5-Dinitrobezoic acid-Mn2+	2.1721	0.9771	1.2500	0.9326	1.9105	1.2600	1.2500	0.9935
2	F-820_3,5-Dinitrobezoic acid-Mn2+	1.3566	1.0232	1.2750	0.9884	1.5306	1.2717	1.2750	0.9947

 

Conclusion

The experiment revealed a notable difference in adsorption capacity between GAC-F-820 and GAC-F-816, with GAC-F-820 demonstrating significantly higher performance. Langmuir, Freundlich, and Temkin models were employed to analyze the adsorption data for Manganese, and the results indicated that the Langmuir model exhibited the best fit, supported by a higher R² value, signifying a robust correlation. Kinetic analysis revealed the success of the Pseudo-second-order model, as evidenced by a high correlation coefficient (R²). These findings highlight the potential of coal-based adsorbents, specifically GAC modified with organic ligands, to advance technologies for removing heavy metal ions from polluted industrial effluents. In summary, the modified GAC surface proves effective in reducing the concentration of Manganese ions in both industrial wastewater and aqueous solutions. The study underscores the importance of considering cost-effectiveness and technical applicability when selecting adsorbents for crucial applications.

Acknowledgment

Authors expressed sincere gratitude towards Prof R.U. Khope, Head Department of Chemistry, SSES Amt’s Science College, Congressnagar, Nagpur (M.S.) India, for their support and encouragement.

Conflict of interest

The author has disclosed no financial or non-financial interest.

Funding Sources

No financial assistance was procured for the preparation of this manuscript.

References

1. Charerntanyarak, L. Water Science and Technology. 1999, 39(10),135-138
   CrossRef
2. 2.Tanong, K.; TranLH, M.G.; Blais, J. F. J. Clean. Prod. 2017, 148, 233-244.
   CrossRef
3. Dey S.; Tripathy, B.; Santosh Kumar, M.; Das, A. P. Environmental Chemistry and Ecotoxicology.2023,5, 55-61.
   CrossRef
4. Razzaque, M. S.  Nutrients. 2018,10(12) ,1863.
   CrossRef
5. Peng, H.; Guo, J. Environmental Chemistry Letters. 2020, 1-4. 
6. Khulbe, K.C.; Matsuura,T .Applied Water Science. 2018, 8-19.
   CrossRef
7. Abo-Farha, S. A.; Abdel-Aal, A.Y.; Ashour, I. A.; Garamon, S. E.  J. Hazard. Mater. 2009, 169,190-194.
   CrossRef
8. Alyuz, B.; Veli, S. J. Hazard. Mater. 2009, 167, 482-488.
   CrossRef
9. Huang, Y.; Zeng, X.; Guo, L.; Lan, J.; Zhang, L.; Cao, D. Separation and Purification Technology. 2018, 462-469.
   CrossRef
10. Sani, A.; Hussaini, K.; Sani, H. M. Applied Water Science .2017, 7, 3151–3155.
    CrossRef
11. Mohamed, S.; Andrzej, G. Acta Scientific Agriculture .2020,4.2, 01-10.
    CrossRef
12. Gunjate, J.K. IOSR-JESTFT. 2016,10, 161-165
    CrossRef
13. Ojedokun, A.T.; Bello, O. S. Water Resources and Industry. 2016, 7-13.
    CrossRef
14. Demirbas, A. Journal of hazardous materials. 2008, 157, 220-229.
    CrossRef
15. Berihun, D. Journal of Materials Science and Engineering. 2017, 6(2), 6–11.
16. Bayuo, J.; Bayuo, K. B.; Pelig-ba, K. B.; Abukari, M. A.  Applied Water Science. 2019, 9(4) ,1–11.
    CrossRef
17. Bayuo, J.; Abukari, M. A.; Pelig-ba, K. B. Journal of Applied Chemistry. 2018, 11, 40–  46.
18. Gautam, A. K.; Markandeya, N.; Singh, B.; Shukla, S. P; Mohan, D. SN Applied Sciences. 2020, 2(2), 1–11.
    CrossRef
19. Grégorio, C.; Eric, L. Environmental Chemistry Letters, 2019,17(1),145-155.
    CrossRef
20. Gunjate, J. K.; Meshram, Y. K.; Khope, R.U.; Awachat, R. S. Materials Today: Proceedings. 2020, 29 ,1150–1155
    CrossRef
21. Furniss, B. S.; Hannaford, A. J.; Smith, P.W.G.; Tatchell, A. R. Vogel’s Textbook of Practical Organic Chemistry. Pearson Education Ltd. 2012, 1348
22. Langmuir, I. Part I. Solids. Journal of the American chemical society. 1916, 38(11), 2221-2295. 
    CrossRef
23. Freundlich, H. M. Over the adsorption in solution. J. Phys. Chem. 1906, 57, 385-471.
24. Temkin, M. I.; Pyzhev, V. Kinetics of ammonia synthesis on promoted iron catalyst. Acta Phys. Chim. 1940, 12, 327–356.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.