PC1D Modeling of Conducting Metal-Doped Semiconductors and the Behavior of MSCs at Varying Temperatures and Size Distributions

Introduction

The study of SCs and PVCs has made significant strides in previous 20years. The development of HESCs has motivated extensive research into many materials, including silicon, CIGS, and group of III-V. The worldwide endeavor to develop a solar cell capable of delivering stable, long-term power has attracted a lot of attention from a variety of quarters. Several hundred times the SRs of group III-V based SC materials in MSCSs led to a 46% efficiency rate at 508 suns for the GIP/GA/GIAP/GIA system [1]. A six-junction cell, LSCs, and a vertically oriented epitaxial heterostructure are examples of recent advancements in SCs technology [2]. Prototype-scale testing has been the norm for high-efficiency MSCSs, and their widespread viable and industrial adoption is still in the works. Here is complex to model and simulate MSCs in various settings. In a MSCs, junction of p-n in the semiconducting deposits (or z-matrix) are arranged from lowest to highest bandgap energy. SRs are absorbed in the short-wavelength region by the first layer because to its high bandgap energy, and in the longer-wavelength region by the subsequent layers [3-6]. In theory, a solar cell’s efficiency would increase if more z-matrix layers were added. Monolithically integrated MSCSs are also possible, as is mechanically stacked it. In MSCS, the efficiency is limited by the tunnel junction between z-matrixes and the matching of electric current and lattice. All of these problems dissolve when the unconsciously stacked MSC is subjected to z-matrix-specific load management. By inserting a conductive layer like ITO between two neighbouring z-matrixes, optical fatalities in unconsciously stacked MSCs can be reduced while maintaining transparency [4-8].

Figure 1: Entering AM1.5d spectra also absorption range from different z-matrices targeting (a) SIMF 1 (=1 Sun) and (b) SIMF 200 (>200 Suns). Click here to View Figure

AlxGa1-xAs/InP/Ge SCs have not been the subject of any experimental or computational studies of MSCs efficiency under temperature and strong radiation. Here, we use PC1D to simulate how AlxGa1-xAs/InP/Ge MSCSs respond to a wide range of environmental conditions, including temperature and light intensity. The author is not aware of any efforts to simulate the results of MSCs via PC1D. This study may overlay the way for the development of a highly efficient, long-lasting, and dependable solar cell [6-9].

Figure 2: Multijunction AlxGa1-xAs/InP/Ge solar cell (a) efficiency against temperature. What is the temperature dependence of the open-circuit voltage of (b) AlxGa1-xAs, (c) InP, and (d) Ge. Click here to View Figure

Method

The review consists of three stages: spectrum preparation, radiation manipulation (both reflected and transmitted), and power generation modeling. The inquiry consists of three stages: spectrum preparation, radiation manipulation (both reflected and transmitted), and power generation modeling.[7]. For one sun’s energy, we used the AM1.5d unswerving solar spectrum to determine occurrence of SI on the 1^st z-matrix aimed at 5 to 200 suns. By means of a blackbody radiation formula, the constant was calculated, which was then used to reconstruct the smoothed AM1.5d SI. We calculated the thickness of the nth cell using PC1D and multiplied it by the total incident radiation [8]. By monitoring the I_SC, V_OC, P_n and the η, we were able to mimic the MSCS’s electrical efficiency. The following is a discussion of the wavelength dependence of the irradiance spectrum of blackbody radiation at the surface of the earth.[9–12].

in which r-Sun for the Sun’s radius, R for the remoteness among the Sun’s center and the Earth’s surface, h for Planck’s constant, and k_B for the Boltzmann constant [13]. By integrating the entire spectrum with a trapezoidal method and holding the intensity constant at 990 W/m2, we can calculate a(λ) . As a result, we can use interpolation to reformat the filtered spectra of AM1.5d [14–15, 18].

The a(λ)  of respectively z-matrix was considered by eq. (2) after the reference:

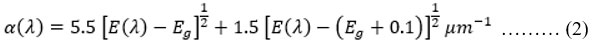
where E(λ) is the energy of an incident photon of wavelength, E_g is the bandgap energy of the coherent z-matrix, and a(λ) is the coefficient  of absorption as a function of wavelength [3–5, 17].

The transmitted intensity at z-matrix l_n+1 is a function of solar energy conventional in z-matrix l_n, z-matrix d_n thickness and z-matrix a_n (λ)  absorption coefficient, l_n (λ) .

where  stands the SI toward the inside the 1^st  z-matrix,  the SI toward the inside the 2^nd , and I₂ the SI toward the inside the 3^rd  [19]. Here, PC1D program was calculate of d_n thickness of n^th cell [20]. In order to surpass the program’s limitations, it will be compulsory to run a significant number of modellings, the exact number of which is dependent on the total number of junctions [21].

Figure 3: Solar cell (a) total efficiency and (b) fall rate as a function of SI multiplication. Click here to View Figure

After performing the multiplication, the total amount of incoming radiation can be premeditated using the following equation [22].

where, after multiplying by a SIMF factor that was set between 1 and 200 suns [23-25], I_mul. is the SI. Here, we ran modelling to determine the MSCS’s electrical efficiency [26], evaluating its I_SC, V_OC, P_n and total efficiency (η). To calculate the total performance of the unconsciously weighted MSCs, we utilize the following equation.

A nonidentical electric current model maximizes  in each z-matrix and total efficiency [1-5, 27], and the MSCS can act out two hypothetical scenarios in which the  through respectively z-matrix is well-adjusted out with or without symmetry. The MSCS’s prior efficiency was 45 %, but the new, different model is predicted to reach efficiency of more than 70 %. Due to simplifications and idealizations and modeling can be viewed as the model of toy, and problems such as hotspot formation, divergence in the  of z-matrix, and failure to account for rises of cutting-edge of resistive losses. [6, 28].

Table 1: the inputs for a typical simulation (at 25 oC and 1 sum’s spectrum irradiance).

Subcell	Energy gap	Thickness	Absorption spectra
A1xGax-1As	1.82	2.78	280-685
InP	1.35	3.5	598-841
Ge	0.66	4.0	872-1773

 

Table 2: Improvements in effectiveness across a spectrum of temperatures and SIMF values.

Temprerature	Gains in productivity between 1 and 100 solar masses, as measured by SIMF (%)	Productivity increases between 100 and 200 suns as measured by SIMF
25	19.01	-2.15
50	20.20	-6.40
75	21.60	-5.00
100	30.57	-6.30

 

Discussions and Results

Other Modelling were in contrast to the source simulation performed at one solar spectral irradiance and 25°C, as recommended in Reference [19]. For all Modelling in this study, Table 1 details the parameters that will be used from the single-sun simulation: subcell thickness, p-doping value, and n-doping value, as well as the absorption spectrum range. Using this baseline simulation as a starting point, we varied the n-doping and p-doping values for further modelling (about 10²⁰/cm³ aimed at doping of n and 10¹⁶/cm³ aimed at doping of p) to get  highest possible total efficiency.

Maximum SI and intensity of the MSCS were calculated using Eqs. (1) and (3). Concentrating solar power helps MSCS solar cells absorb more light by raising their temperature [1-7, 17, 24]. Inclusive MSCS efficiency increased in a nonlinear fashion with SIMF, peaking at roughly 100 SI and then steadily falling as the system reached saturation [1-4]. Comparable to the stochastic retort of MSCs to variations in SIMF [2–5, 23], SCEs decline as of – 0.13 % /°C to – 0.07 % /°C as soon as the SIMF raises as of 1 to 100 suns, in addition subsequently increase in the direction of – 0.10 % /°C on 200 suns.

Figure 4. Comparison of V–I pro9le on 25°C (solid line) and 75°C (dashed line) and different SIMF aimed at (a) Al0.3Ga0.7As, (b) InP, and (c) Ge, and (d) I_SC on different SIMFs.

By 25 °C – 75 °C aimed at SIMFs among 50 and 200 suns [5, 25], the V–I performance of respectively z-matrix is shown in figure 4. Maximum SI and intensity of the MSCS were calculated using Eqs. (1) and (3). Concentrating the sun’s rays on MSCS solar cells raises their operating temperature and enhances their ability to absorb light [6, 17]. The inclusive efficiency of the MSCS increased in a nonlinear fashion with growing SIMF, success a maximum somewhere upto 100 SI and then gradually falling when the saturation point was reached. Analogous to the stochastic retort of MSCS to variations in SIMF [1, 18], the rate of SCEs degeneration declines as of – 0.13 % /°C towards – 0.07 % /°C after the SIMF climbs from 1 to 100 suns, and then increases to – 0.10 % /°C at 200 suns. Next to 25°C ® 75°C, also aimed at SIMFs among 50 and 200 suns, here figure shows the V–I performance of respectively z-matrix [1–5, 26–28].

Conclusion

We have modelled the presentation of AlxGa1-xAs/InP/Ge MSCSs under different spectral irradiance in addition temperatures, and our results are in fair agreement with those of previous studies focusing on III-V based MSCSs. In addition to a nonlinear retort to the product of spectrum irradiance and temperature, multijunction solar cells showed a linear (negatively sloped) response to Voc and overall efficiency as a function of temperature (SIMF). Subcellular temperature sensitivity can also be mitigated by the use of spectral irradiance multiplication. The single-diode rough calculation model agrees with the quasi retort of  also overall competence to SIMF. We show that, under the material parameter expectations hand-me-down here, AlxGa1-xAs/InP/Ge MSCSs have the more efficiency when illuminated at 100 suns and 25°C, which may be preferable in some instances equated to experimentally obtainable data.

Acknowledgements

The researchers acknowledge the assistance of the Kalinga University Physics Department in Naya Raipur (CG), India.

Conflicts of Interest

There are no potential conflicts of interest with the writers. The process of gathering information, analyzing it, writing it up, and deciding if the findings should be made public.

References

1. Sun, Z., Chen, X., He, Y., Li, J., Wang, J., Yan, H., & Zhang, Y. (2022). Toward Efficiency Limits of Crystalline Silicon Solar Cells: Recent Progress in High‐Efficiency Silicon Heterojunction Solar Cells. Advanced Energy Materials, 12(23), 2200015.
   CrossRef
2. Battaglia, C., Cuevas, A., & De Wolf, S. (2016). High-efficiency crystalline silicon solar cells: status and perspectives. Energy & Environmental Science, 9(5), 1552-1576.
   CrossRef
3. De Wolf, S., Descoeudres, A., Holman, Z. C., & Ballif, C. (2012). High-efficiency silicon heterojunction solar cells: A review. green, 2(1), 7-24.
   CrossRef
4. Sahu, G., Dewangan, K., Johan, S., Verma, A. (2023 May). Simulating the Performance of AlxGa1-xAs/InP/Ge MSCS Under Variation of SI and Temperature. European Chemical Bulletin, 12 (Special Issue 4), 7914-7923.
5. Verma, A., Diwakar, A. K., & Patel, R. P. (2019). Synthesis and characterization of high-performance solar cell. International Journal of Scientific Research in Physics and Applied Sciences, 7(2), 24-26.
   CrossRef
6. Kale, A. S., Nemeth, W., Harvey, S. P., Page, M., Young, D. L., Agarwal, S., & Stradins, P. (2018). Effect of silicon oxide thickness on polysilicon based passivated contacts for high-efficiency crystalline silicon solar cells. Solar Energy Materials and Solar Cells, 185, 270-276.
   CrossRef
7. Lal, M., & Gangotri, K. M. (2022). Innovation in progressive study for prospective energy source through photo‐galvanic‐system: d‐Xylose+ MB+ Brij‐35+ NaLS. International Journal of Energy Research, 46(14), 19538-19547.
   CrossRef
8. Ho, W. J., Lu, P. C., & Liu, J. J. (2022). Improving the performance of textured silicon solar cells through the field‐effect passivation of aluminum oxide layers and up‐conversion via multiple coatings with Er/Yb‐doped phosphors. International Journal of Energy Research, 46(1), 278-289.
   CrossRef
9. Ballif, C., Haug, F. J., Boccard, M., Verlinden, P. J., & Hahn, G. (2022). Status and perspectives of crystalline silicon photovoltaics in research and industry. Nature Reviews Materials, 7(8), 597-616.
   CrossRef
10. Masuko, K., Shigematsu, M., Hashiguchi, T., Fujishima, D., Kai, M., Yoshimura, N., … & Okamoto, S. (2014). Achievement of more than 25% conversion efficiency with crystalline silicon heterojunction solar cell. IEEE Journal of Photovoltaics, 4(6), 1433-1435.
    CrossRef
11. Verma, A., Diwakar, A. K., Patel, R. P., & Goswami, P. (2021). Characterization CH3NH3PbI3/TiO2 nano-based new generation heterojunction organometallic perovskite solar cell using thin-film technology. In AIP Conference Proceedings (Vol. 2369, No. 1, p. 020006). AIP Publishing LLC.
    CrossRef
12. Zhu, H., Kalkan, A. K., Hou, J., & Fonash, S. J. (1999). Applications of AMPS-1D for solar cell simulation. In AIP Conference Proceedings (Vol. 462, No. 1, pp. 309-314). American Institute of Physics.
    CrossRef
13. Rodrigues, E. M. G., Melicio, R., Mendes, V. M. F., & Catalao, J. P. (2011). Simulation of a solar cell considering single-diode equivalent circuit model. In International conference on renewable energies and power quality, Spain (pp. 13-15).
    CrossRef
14. Santbergen, R., Meguro, T., Suezaki, T., Koizumi, G., Yamamoto, K., & Zeman, M. (2017). GenPro4 optical model for solar cell simulation and its application to MSCS. IEEE journal of photovoltaics, 7(3), 919-926.
    CrossRef
15. Mohammed, S. S. (2011). Modeling and Simulation of Photovoltaic module using MATLAB/Simulink. International Journal of Chemical and Environmental Engineering, 2(5).
16. Rathore, J., Rakesh Kumar, A., Sharma, P., & Lal, M. (2022). Study of Electrical Output in Photogalvanic Cell for Solar Energy Conversion and Storage: Lauryl Glucoside-Tartrazine-D-Fructose System. Indian Journal of Science and Technology, 15(23), 1159-1165.
    CrossRef
17. Patel, J., & Sharma, G. (2013). Modeling and simulation of solar photovoltaic module using matlab/simulink. International Journal of Research in Engineering and Technology, 2(03), 2319-1163.
    CrossRef
18. Bellia, H., Youcef, R., & Fatima, M. (2014). A detailed modeling of photovoltaic module using MATLAB. NRIAG journal of astronomy and geophysics, 3(1), 53-61.
    CrossRef
19. Awodugba, A. O., Sanusi, Y. K., & Ajayi, J. O. (2013). Photovoltaic solar cell simulation of shockley diode parameters in matlab. International Journal of Physical Sciences, 8(22), 1193-1200.
20. Verma, A., Diwakar, A. K., & Patel, R. P. (2020). Characterization of Photovoltaic Property of a CH3NH3Sn1-xGexI3 Lead-Free Perovskite Solar Cell. In IOP Conference Series: Materials Science and Engineering (Vol. 798, No. 1, p. 012024). IOP Publishing.
    CrossRef
21. Zainal, N. A., & Yusoff, A. R. (2016). Modelling of photovoltaic module using matlab simulink. In IOP Conference Series: Materials Science and Engineering (Vol. 114, No. 1, p. 012137). IOP Publishing.
    CrossRef
22. Al-Ezzi, A. S., & Ansari, M. N. M. (2022). Photovoltaic Solar Cells: A Review. Applied System Innovation, 5(4), 67.
    CrossRef
23. Tayeb, A. M., Solyman, A. A., Hassan, M., & el-Ella, T. M. A. (2022). Modeling and simulation of dye-sensitized solar cell: Model verification for different semiconductors and dyes. Alexandria Engineering Journal, 61(12), 9249-9260.
    CrossRef
24. Needell, D. R., Ilic, O., Bukowsky, C. R., Nett, Z., Xu, L., He, J., … & Atwater, H. A. (2018). Design criteria for micro-optical tandem luminescent solar concentrators. IEEE Journal of Photovoltaics, 8(6), 1560-1567.
    CrossRef
25. Nishioka, K., Takamoto, T., Agui, T., Kaneiwa, M., Uraoka, Y., & Fuyuki, T. (2006). Annual output estimation of concentrator photovoltaic systems using high-efficiency InGaP/InGaAs/Ge triple-junction solar cells based on experimental solar cell’s characteristics and field-test meteorological data. Solar Energy Materials and Solar Cells, 90(1), 57-67.
26. Verma, A. K., Goswami, P., Patel, R. P., Das, S. C., & Verma, A. (2020). Futuristic Energy Source Of CTB (Cs2TiBr6) Thin Films Based Lead-Free Perovskite Solar Cells: Synthesis And Characterization. Solid State Technology, 63(6), 13008-13011.
    CrossRef
27. Premkumar, M., Chandrasekaran, K., & Sowmya, R. (2020). Mathematical modelling of solar photovoltaic cell/panel/array based on the physical parameters from the manufacturer’s datasheet. International Journal of Renewable energy development, 9(1), 7.
    CrossRef
28. Banik, A., Shrivastava, A., Potdar, R. M., Jain, S. K., Nagpure, S. G., & Soni, M. (2022). Design, modelling, and analysis of novel solar PV system using MATLAB. Materials today: proceedings, 51, 756-763.
    CrossRef

---

This work is licensed under a Creative Commons Attribution 4.0 International License.