Rheology of Non-Additive Olive Oil used as a Biodegradable Lubricant

Introduction

Olive oil (the fruit of Olea europaea; family Oleaceae) is extracted from olives through a very simple process: the fruits are cold-pressed to extract the oil. Modern methods also involve crushing and mixing the olives, then separating the oil from the pulp by centrifugation.

After centrifugation, small amounts of oil remain in the olive cakes – this can be extracted using chemical solvents and is known as olive cake oil. After the recording of the rheograms, a delicate stage follows, namely their interpretation. There are many rheological models for interpreting data. For most fluids, the most widely used model is a three-parameter model, described by the Herschel – Bulkley equation ^1–5:

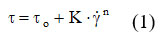
In this model, τ_o represents the voltage or the effort of flow, signifying the minimum voltage that must be applied to initiate the flow. Obviously, being a voltage it is measured in Pascali (1 Pa = 1 N. m^-2). K is the consistency coefficient, the value of which depends on the nature and temperature of the fluid. It is measured in Pa. sⁿ, formally being a viscosity. The flow behavior index is the exponent of the shear rate, n. It is a dimensionless quantity, which depends on the nature of the fluid, its value being very little influenced by temperature.

The Herschel-Bulkley model is simplified and will take the form of the Ostwald model or the law of power:

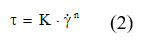
Fluids for which the flow behavior index is unitary, as in Newtonian fluids, but there is flow effort (or tension) ( τ_o > 0) they are called plastic fluids or Bingham plastic. For such a material, its behavior is like an elastic solid when the stress is below the value of the flow stress (or stress) τ_o. For voltages greater than the flow voltage, the mathematical expression for the model is ^6–8: 

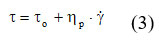
This mathematical expression of the Bingham model derives from the Herschel – Bulkley equation when n = 1, and K = η p. Given that the flow behavior index is unitary, the unit of measurement for the consistency index (K) is Pa. that is, the unit of measurement for viscosity. This is why K is replaced by η _p ^9–12.

Material and methods

Cold pressed olive oil was studied with the Haake VT 550 viscometer at increasing shear rates. From the dynamic viscosity and the shear rate, we determined the shear stress at each temperature. By linearizing the data obtained experimentally, we determined two rheological models that faithfully describe the behavior of olive oil.

Results and discussion

Figures 1-7 show linear fitting of experimental data of non-additive olive oil used as a biodegradable lubricant. As can be seen in the rheograms, the shear stress increases with increasing shear rate and has a linear dependence.  

Figure 1: Linear fitting of experimental data of olive oil to temperature 313K. Click here to View figure

Figure 2: Linear fitting of experimental data of olive oil to temperature 323K. Click here to View figure

Figure 3: Linear fitting of experimental data of olive oil to temperature 333K. Click here to View figure

Figure 4: Linear fitting of experimental data of olive oil to temperature 343K. Click here to View figure

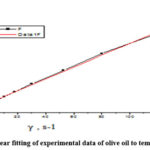Figure 5: Linear fitting of experimental data of olive oil to temperature 353K. Click here to View figure

Figure 6: Linear fitting of experimental data of olive oil to temperature 363K. Click here to View figure

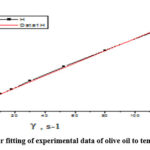Figure 7: Linear fitting of experimental data of olive oil to temperature 373K. Click here to View figure

The article proposes two equations obtained by linear and exponential fitting of the experimental data:

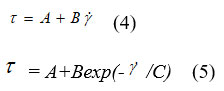
Table 1: Rheological parameters of the model (4) for olive oil.

Temperature, K	Rheological model constants (4)		R2
	A	B
313	40.8707	19.8184	0.9999
323	45.5434	11.2528	0.9995
333	38.8396	9.6028	0.9997
343	38.9844	8.9793	0.9994
353	38.2732	8.4015	0.9989
363	39.5068	7.7240	0.9989
373	33.0540	7.5880	0.9996

 

Table 2: Rheological parameters of the model (5) for olive oil.

Temperature, K	Rheological model constants (5)			R2
	A	B	C
313	-2.1256E7	2.1256E7	-1.0726E6	0.9999
323	8226.2569	-8194.2029	667.7298	0.9995
333	-9428.5756	-9428.5756	921.9126	0.9997
343	5055.5401	-5031.0308	499.1903	0.9998
353	3581.1580	-3561.7138	361.8749	0.9999
363	3159.7222	-3138.4422	344.0841	0.9998
373	5327.3930	-5303.8596	638.4288	0.9999

 

Applying model (4), the R² have values between 0.9989 and 0.9999, which demonstrates that this model correctly describes the rheological behavior of unadditive olive oil used as a biodegradable agent.

Model (5) has the values of the R² between 0.9995 and 0.9999, dedi and it correctly describes the rheological behavior of olive oil. The two models were obtained by linear and exponential fitting of the experimental data.

Conclusions

The article proposes two rheological models obtained by linear and exponential fitting of unadditive olive oil used as a biodegradable lubricant. The two models found faithfully describe the non-Newtonian behavior of unadded olive oil because R² has values close to one. The olive oil was obtained by cold pressing and then the fruits were separated by centrifugation.

References

1. Rao  M.A. 1977,  J. Text. Stud., 8, 257 – 282
   CrossRef
2. Boger D.V. 1994, Yield stress measurement, Lecture Series 1994-03 “Non-Newtonian Fluid Mechanics”, Von Karman Institute for Fluid Mechanics, Belgium, February 21-25, 24.
3. Ma L., Barbosa-Canovas G.V., 1993, Revista Espaniola de Ciencia y Tecnologia de Alimentos, 33(2), 133 – 163
4. Holomb D.N., Tung M.A. 1991. Rheology, chapter in “Encyclopedia of Food Science and Technology”, volume 4, John Wiley and Sons, Inc., 2258-2264
5. Velez-Ruiz J.F., Barbossa-Canovas G.V. 1997,, Critical Reviews in Food Science and Nutrition, 37(4), 311 – 359
   CrossRef
6. Kokini, J.L. 1992. Rheological properties of foods, cap. 1 în “Handbook of Food Engineering” (D.R. Heldman, D.B. Lind, eds.), Marcell Dekker, New York, 1 – 38
7. Schowalter, W.R., Christensen, G. 1998, J. Rheol., 42(4), 865-870
   CrossRef
8. Dimonte, G., Nelson, D., Weaver, S., Schneider, M., Maudlin, F., Gore, R., Baumgardner, J.R. 1998, J. Rheol., 42(4), 727-742
   CrossRef
9. Stanciu I., 2019, Journal of Science and Arts, 3(48), 703-708.
   CrossRef
10. Stanciu I., 2019, Journal of Science and Arts, 4(49), 938-988.
11. Stanciu I., 2011,  Journal of Science and Arts, 1, 55-58.
12. Stanciu I., 2018, Journal of Science and Arts, 18(2), 453-458.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.