Calculation of Vibrational Energies of AlH2 Using U(2) Lie Algebraic Approach

Introduction               

The interpretation and analysis of the molecular spectra of molecules is a fascinating research area of molecular physics. Vibrational energies have played anvital role in both theoretical and experimental techniques due to their diverse applications. Vibrational spectra is currently undergoing an exciting period of renewed attention, fuelled by the rapid development of sophisticated experimental techniques. Due to their numerous applications in the research study of vibrational energies of molecules, one and three dimensional [U(2), U(4)] Lie algebraic approaches have grabbed the attention of a larger scientific community. With the use of these approaches, one can easily obtain the vibrational and rotational degrees of freedom in a physical problems¹. The vibrational energies of a molecule are represented by the eigenvalues of the Hamiltonian matrix. These approaches are successful in the research study of polyatomic molecules vibrational spectra ^2-7. The vibrational and rotational energies are treated simultaneously in the U(4) Lie algebraic approach. When a molecule has more than four atoms, this approach becomes more complicated. To analyze the vibrational energies of aluminum dihydride, this limitation led us to utilize the U(2) Lie algebraic approach.

One dimensional Lie algebraic approach

A bent molecule with C_2v point group symmetry is aluminium dihydride.This aluminium dihydride molecule contains the symmetry species, A₁(Symmetric Stretch), B₂ (Antisymmetric Stretch), and A₁ (Bend).

For n vibrational modes, the general Hamiltonian ^8-11 is

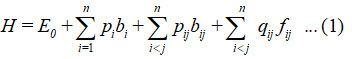
In equation (1), b_i and b_ij are uncoupled and coupled bonds invariant operators, respectively, and known as

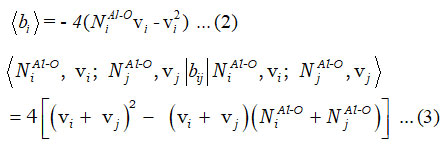
Majorana operator f_ij consist diagonal and non-diagonal matrix elements and it is useful to articulate the pair of local mode interactions ¹². 

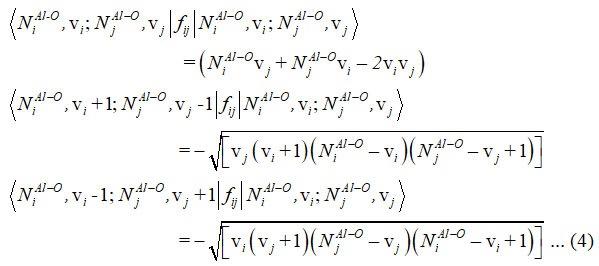
For two (Al-O) stretching vibrations of aluminumdihydride, the Hamiltonian operator written as

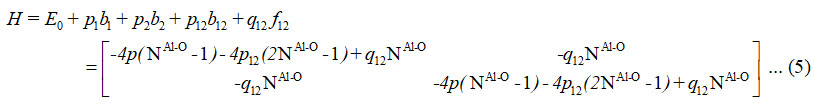
From spectroscopic data algebraic parameters P₁ ,P₂, P₁₂ and q₁₂  (cm^-1) are determined . Two bonds (Al-O) are equivalent in the aluminum dihydride. As a result, we consider P₁ = P₂ = P and Vibron number, N₁^Al-o = N₂^Al-o= N^Al-o in equations (2), (3) and (4).

Results and Discussion

The parameter p is determined using the energy equation (6)

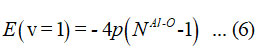
and the value of q₁₂ calculated from the relation,

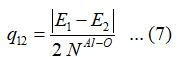
Where E₁, E₂ are the aluminum dihydride symmetric and antisymmetric vibrational energies, respectively. The number N_i for stretching bonds of aluminum dihydride is calculated from the relation,

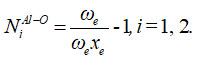
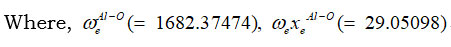
are correspondingly, vibrational harmonic and an harmonic spectroscopic constants ¹³.

The Lie algebraic approach is utilized to compute the vibrational energies of aluminium dihydride (in higher overtones and combinational bands), as indicated in the tables (1), (2) and (3).

Table 1: Vib. frequencies in fundamental mode (in cm^-1).

Vib. Mode	Symmetry	Experimental#	Computed
v1 (Symmetric stretch)	A1	1788	1788.38
v2 (bend)	A1	760	758.7162
v3(antisymmetric stretch)	B1	1828.6	1827.9732

^#webbook.nist.gov/cgi/cbook.cgi?ID=C14457659&Units=SI&Mask=800#Electronic-Spec

Table 2: Vib. frequencies (overtone) (in cm^-1)

Overtone	Vib. mode
	Symmetric stretch (A1)	Bend (A1)	Antisymmetric stretch(B1)
1	2v1(3563.761)	2v2(1509.995)	2v3(3644.028)
2	3v1(5335.594)	3v2(2237.022)	3v3(5429.990)
3	4v1(7091.096)	4v2(2921.258)	4v3(7258.733)
4	5v1(8826.294)	5v2(3620.721)	5v3(8089.413)
5	6v1(10622.643)	6v2(4430.447)	6v3(9758.083)

 

Table 3: Combinational frequencies (in cm^-1)

Combinational Band	Computed	Combinational Band	Computed
v1+ v2	2542.075	2v1+ v2	4317.456
v1+ v3	3615.685	v2+2v2	2258.336
v2 + v3	2580.668	v2 +2v3	4397.723
v1+2v1	5352.473	2v1+ v3	5391.066
v1+ 2v2	3293.354	v3+ 2v2	3331.947
v1+ 2v3	5432.740	v3+ 2v3	5471.333

 

Table 4: Parameters

NAl-O(stretch)	58
NAl-O(stretch)	38
P(stretch)	-7.9275
P(bend)	-5.1351
P12(stretch)	0.0415
P13(bend)	-1.2968
q12(stretch)	0.3327
q13(bend)	1.9621

Conclusion

We compared the examined data which was in the table (1) with the calculated fundamental vibrational energies of the aluminumdihydride.

Vibrational energies up to theharmonic level six and combinational bands upto the harmonic level three were described using the one dimensional [U(2)] Lie algebraic approach in tables (2) and (3).

Acknowledgment

The author, J. Vijayasekhar, would like to thanks GITAM(Deemed to be University), Vishakhapatnam, India, for providing financial assistance of this study under GITAM: Research seed Grants.

Conflicts of Interest

The authors declare no conflict of interest.

References:

1. Iachello, F.; Oss, S.; Lemus, R.J. Mol. Spectrosc.1991, 149 (1), 132-151.
   CrossRef
2. Karumuri, S.R.; Sravani, K.G.; Vijayasekhar, J.; Reddy, L.S.S.  Acta Phys. Pol. A. 2012, 122 (1), 49 52.
   CrossRef
3. Karumuri, S. R.;Srinivas, G.;Vijayasekhar, J.; Rao, V. U. M.;Srinivas, Y.; Sunil Babu, K.; Kumar, V. S. S.;Hanumaiah, A. Chin. Phy. B.2013, 22(9), 090304(1-8).
   CrossRef
4. Iachello, F.; Oss, S.J. Mol. Spectrosc. 1992, 153 (1–2), 225-239.
   CrossRef
5. Balla, M.R.; Vijayasekhar, J. Mol. Phys. 2021, 115 (5), e1828634.
   CrossRef
6. Balla, M.R.; Vijayasekhar, J. PolycyclAromat Compd. 2021. 42(7), 4684-4699
   CrossRef
7. Balla, M.R.; Venigalla, S.; Jaliparthi, V. Acta Phys. Pol. A. 2021, 140 (2), 138-140.
   CrossRef
8. Oss, S. Adv. Chem. Phys.1996, 93, 455-649.
9. Iachello, F.; Levine, R. D. Oxford University Press, Oxford.1995.
10. Vijayasekhar, J.;Balla, M.R. Spectrochim. Acta A. 2022, 264, 120289(1-8).
    CrossRef
11. Vijayasekhar,J.Ukr. J. Phys. Opt. 2022, 23(3), 126-132.
    CrossRef
12. Vijayasekhar,J; Srinivas, N; Kumar, A. K. Orient. J. Chem. 2022, 38(1): 204-206.
    CrossRef
13. Irikura, K.K. J. Phys. Chem. Ref. Data. 2007, 36(2), 389-398.
    CrossRef

---

This work is licensed under a Creative Commons Attribution 4.0 International License.