Rheology of Gums Used in the Food and Flour Industry for "Tortillas"

Introduction

Food gums are hydrophilic colloids, which due to their functional properties are used in the food industry ^1-5. Their most important functional properties are: water retention capacity, decrease in evaporation rate, change in cooling rate, change in the formation of ice crystals, regulation of rheological properties, participation in chemical processes, keep insoluble particles in suspension, stabilize foams and emulsions ^6-9.

Many seemingly homogeneous liquids are composed of particles with irregular shapes or inhomogeneities of the liquid phase. On the other hand, there are polymer solutions with long or curly molecular chains. At rest, all these materials are characterized by an irregular internal structure and consequently oppose the flow, having high viscosity.

This article presents the rheological behavior of food gums used in the food industry as well as flour for “tortillas”.

Material and methods

Experimental data were obtained with a Haake RV20 rotary viscometer with a cone-plate system. The range of shear speeds for which the determinations were made was between 24 and 3177s^-1, and the shear stresses between 2.2 and 116.9Pa.

Results and discussion

Table 1 shows the rheological parameters for the aqueous solutions of some food gums derived from the power law.

The form of the Ostwald model or the law of power: 

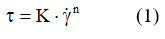
The expression of the law of power (relation 2) can be linearized by logarithm:

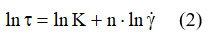
Obviously, mathematically, addiction τ = f(ln γ)  is a line, from the intersection to the ordinate obtaining the value of ln K, and from the slope the value of n. This is one of the most used calculation procedures for K and n. We exemplify with the interpretation of some recent data from the literature ¹⁰, concerning rheological studies for flour from which tortilla paste is obtained. Experimental data obtained for addiction τ = f(γ)  are shown in both Table 2 and Figures 1 ¹⁰ and 3.

Table 1:  Rheological parameters of aqueous solutions of food gums obtained from the law of power.

Food gum	Concentration (%)	Temperature (°C)	K (Pa . sn)	n
Furcellaran	0.8	25.4	0.49	0.55
	1.2	24.4	2.82	0.45
	1.6	24.4	15.1	0.24
Guar	0.5	24.4	1.12	0.45
	1.0	24.3	20.3	0.17
	1.5	24.7	46.4	0.16
	2.0	24.5	10.2	0.094
Xantan	0.5	25.3	0.93	0.37
	0.75	24.5	1.76	0.32
	1.0	24.4	2.74	0.29
	1.2	24.7	3.98	0.26

Figure 1: Rheological behavior of pasta obtained from “tortillas” flour:  Model RSM as and Robertson and Stiff’s Model RPM as Rational Polynomial Model Click here to View figure

Table 2 contains in the first two columns, the experimental data obtained by the authors on a Haake RV20 rotary viscometer with a cone-plate system. The other 4 columns in the table, as well as figures 2 and 3 were obtained by us with the Origin 7.0 program, based on the data taken from Nunez-Santiago’s work [10]. With the logarithmic values of the shear stress and speed, the dependence from relation (2) was plotted in figure 2. By linear correlation (R = 0.9647) the values for n (0.776) and K (0.317) were obtained, respectively.

Table 2: Experimental values for the influence of shear rate on shear stress obtained from rheological measurements for pasta obtained from “tortillas” flour t₁  and t₂  are calculated values of the shear stress with the help of K and n obtained by linearization, respectively by the nonlinear regression applied to Ostwald’s model.

Shear rate(s-1)	Shear stress t (Pa)	Shear stress (Pa)	Shear stress ln t(Pa)	Shear stress t1 (Pa)	Shear stress t2 (Pa)
24	2.2	3.17805	0.78846	3.73	6.68
32	2.7	3.46574	0.99325	4.66	7.92
40	3.9	3.68888	1.36098	5.55	9.03
51	8.6	3.93183	2.15176	6.70	10.42
68	10.8	4.21951	2.37955	8.38	12.33
89	13.7	4.48864	2.6174	10.32	14.45
114	17.5	4.7362	2.8622	12.51	16.72
149	19.8	5.00395	2.98568	15.40	19.56
191	25.3	5.25227	3.2308	18.67	22.64
245	27.2	5.50126	3.30322	22.65	26.21
318	33.9	5.76205	3.52342	27.73	30.55
403	36.4	5.99894	3.59457	33.32	35.12

 

Because n is subunit, the paste obtained is a pseudoplastic fluid. Using the power law expression (relation 1) the values for voltage ( τ ₁) in the penultimate column were calculated. It can be seen that at high shear rates there is a big difference between the experimental values (2nd column) and the calculated values (penultimate column). The same differences can be seen in the graph, as can be seen in Figures 1 and 3. This means that, for this product, the linearization of the power law does not allow obtaining correct values for K and n. The graph in Figure 2 itself confirms this conclusion. And in the original graph in the paper, figure 1, the same deviation of the calculated values of the shear stress is observed, compared to the experimental ones.

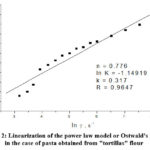Figure 2: Linearization of the power law model or Ostwald’s model in the case of pasta obtained from “tortillas” flour Click here to View figure

Instead, by nonlinear regression and a large number of iterations, using a function identical to that of the law of power, we managed to obtain with the program Origin 7.0, more correct values, which allowed the calculated values (last column) to be closer of the experimental ones, and the calculated curve to overlap excellently (R² = 0.9934) over the experimental rheogram (figure 2). The new values obtained for the two rheological parameters are n = 0.588 and K = 1.032 Pa. sⁿ.

Similar correlations with ours were obtained by Nunez-Santiago and collaborators, using two other models. The first of these is the Robertson and Stiff model ¹¹, for which the correlation factor is R² = 0.996 and the overlap of the calculated curve over the experimental one is very good. The second model is the rational polynomial model ¹². The correlation factor is R² = 0.998 and the overlap of the calculated curve (RPM model in figure 1) over the experimental one is excellent.

Robertson and Stiff’s model [11] can be written:

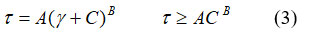
Where A, C and B are parameters according to the rheological theory proposed by Robertson and Stiff.

The rational polynomial model (RPM) has the form:

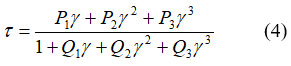
where P₁, P₂, P₃, Q₁, Q₂ and Q₃ are parameters that  strongly depend on the shear rate according to the rheological theory proposed by Kumar ^10-16.

Figure 3: Comparison of curves calculated with values obtained by linearizing Ostwald’s model (dotted curve), respectively by nonlinear regression of the  same model (continuous curve) ○ – experimental points. Click here to View figure

Conclusions

From the obtained data it can be concluded that both food gums and pasta obtained from flour for “tortillas” have a pseudoplastic fluid behavior and follow Ostwald’s model.

Linearization of the power law model or Ostwald’s model in the case of pasta obtained from “tortillas” flour led to the following parameters: n = 0.776, lnK = -1.14919, k = 0.317 and R = 0.9647.

References

1. Barak S., Mudgil D., & Taneja S., 2020, Journal of the Science of Food and Agriculture, 100(7), 2828-2835.
   CrossRef
2. Rao M.A., & Kenny J.F., 1975, Canadian Institute of Food Science and Technology Journal, 8(3), 142-148.
   CrossRef
3. Sánchez V.E., Bartholomai G.B., & Pilosof A.M.R., 1995, LWT-Food Science and Technology, 28(4), 380-385.
   CrossRef
4. Qi X., Zhang M., Su T., Pan W., Tong X., Zeng Q., … & Shen J., 2020, Journal of agricultural and food chemistry, 68(12), 3770-3778.
   CrossRef
5. Clemens R.A., & Pressman P., 2017, Nutrition Today, 52(1), 41-43.
   CrossRef
6. Kayacier A., & Dogan M., 2006, Journal of Food engineering, 72(3), 261-265.
   CrossRef
7. Li X., Xing Y., Sun Q., Chu L., & Xiong L., 2015, Starch‐Stärke, 67(5-6), 399-406.
   CrossRef
8. Wallingford L., & Labuza T.P.,1983, Journal of Food Science, 48(1), 1-5.
   CrossRef
9. Farkas E., Glicksman M., 1967, Food Technol., 21, 535-538
10. Nunez-Santiago M.C., Santoyo E., Bello-Perez L.A., Santoyo-Gutierrez S., 2003, Journal of Food Engineering , 60, 55–66
    CrossRef
11. Robertson R.E., Stiff H.A., 1976,  Society of Petroleum Engineers Journal, 2, 31–37
    CrossRef
12. Kumar A., Saboo S., Sheth S., Pilehvari A., Serth R., 2000, Chemical Engineering Communication, 183, 99–117.
    CrossRef
13. Stanciu I., 2019, Journal of Science and Arts, 3(48), 703-708.
14. Stanciu I., 2019, Journal of Science and Arts, 4(49), 938-988.
    CrossRef
15. Stanciu I., 2011,  Journal of Science and Arts, 1, 55-58.
16. Stanciu I., 2018, Journal of Science and Arts, 18(2), 453-458.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.