Structural and Vibrational Characteristics of Solid Naphthalene (C10H8) Through the Use of van der Waals three-body force shell (VTBFS) Model

Introduction

Naphthalene crystal has a monoclinic structure. The huge varieties of Organic materials and easiness with which they can be modified for various desired purposes with minimum limitations have increased their practical utility and gave rise to a new range of technical applications in science and technology. ^1,2. The author are investigated on the characterisation and lattice dynamics properties of organic crystal through use of VTBFS model for naphthalene. Flexible crystals made of definite order of arrangement of organic molecules bonded to each other through weak bonds of interaction are called organic crystals. Based on the constituent molecules there arises a possibility of hydrogen bond and di-polar interactions as well which contributes to the stability of their crystal structure ³. This design is applied to various engineering materials to produce organically made electronic devices like solar cells, light emitting diodes and sometimes they are also used as an important material in preparation of different drugs for medical use.

Theory

Organic crystals consist of both vibrational and translational motion of the constituent molecules. Phonons are the smallest discrete quantity of vibrational properties of a crystal lattice ^4,5. Vibrational motion of the constituent molecules of these crystals leads to two modes. The external one corresponds to the vibrations of the lattice and is studied based on the different types of phonons contained in the organic crystal.

Figure 1: Unit Cell Naphthalene Crystal. Click here to View figure

A theoretical approach is adopted for calculating the spectra and its dispersion of the phonons as the basic step for study. Theoretical study of calculation of the spectra and dispersion of the phonons is always initiated by considering a gas model in which the molecules are taken in fixed or invariable form with mass and moment of inertia linked with the van-der-Waals force ^6,7. The phonon frequencies of all phonons in the organic crystals are less than that of internal modes and less than the frequencies of the molecules which have covalent bonding. All phonons in the crystal lattice are featured by individual dispersion relation and these are designated as the dispersion branches of the phonons ^8,9,10. Optical phonons can be raised to higher energy states thermally, but they can be excited more efficiently by the inelastic neutron scattering method, scattering through Raman effect, infrared scattering methods etc. these methods give a quantitative approach towards the determination of the frequency spectrum and dispersions of the phonons of the crystal lattice. For the simplicity of calculation, we will only determine the frequencies of only those phonons having the wave vector zero approximately.

Materials and Method

Since organic crystals are flexible, they have large coefficient of thermal growth. This is because their constituent molecules are bonded together by van-der-Waals interaction. The dependence of naphthalene crystal on temperature is given by the relation V (T) = A.T² + B where V & T are volume and temperature, A and B are constants which vary from crystal to crystal based on the size of the molecules in the crystal lattice. Because of changes in the volume of the crystal under investigation and with change in temperature and pressure the parameters of lattice as well as the external phonon frequencies change.  As the temperature rises, there occurs an expansion in the crystal structure due to which the phonons have lower frequencies. The expression for crystal potential per unit cell is given as   

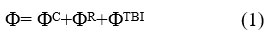
Φ^C is long-range Coulomb interaction potentia1 is as

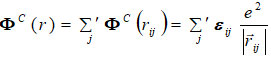
The analytical expressions by the inverse and exponential power laws for the repulsive energy are given as

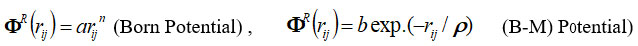
where, a (or b) and h(orr) are strength and hardness parameters and term Φ^TBI long-range TBI potential interaction is as

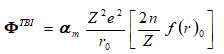
term f(r)₀ is equilibrium wave electron -functions. On consideration of single ion only i.e polarizable and deformable consideration by Singh et.al ^11,12 presented and modified the secular determinant equation

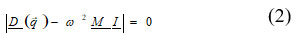
Here D (q) is the (6 x 6) dynamical matrix for Rigid Shell model. The dipole-dipole (VWI) energy up to second neighbour is expressed as:

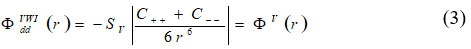
using secular equation (2) for elastic constants equation can give as:

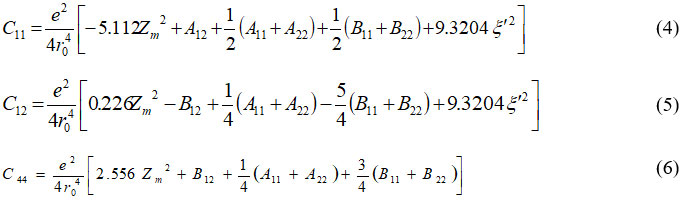
The phonon density is given as   

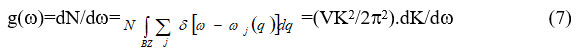
and

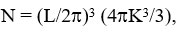
Table 1: Input data and density of states frequency data.

Input data for Naphthalene		Frequency (THz)	Frequency in (a.u)
Properties	Values for Naphthalene	0.0699	0.0306
C11	8.59	0.9523	0.0283
C12	6.43	1.8340	0.0568
C44	2.95	2.2915	0.1172
ro	3.62 Å	3.6226	0.5753
a	7.65 Å	4.1833	0.7585
b	4.77 Å	4.3984	0.6041
c	7.48 Å	4.6645	1.3419
β	125.3 Å	5.2170	1.8943
V	301.32 Å	5.5469	2.9396
		5.7777	3.6775
		6.0438	4.4153
		6.3105	5.1223
		6.5807	5.6754
		6.8088	4.9364
		7.0375	4.1666
		7.6274	6.2266
		7.6457	6.3192
		7.6640	7.7650
		7.9057	8.0105
		8.0285	7.2410
		8.2403	5.6404
		8.3631	4.8709
		8.5912	4.1318
		8.8546	3.3927
		9.1179	2.6535
		9.3460	1.9145

Result and Discussion

The model parameter is use to calculate frequency along with uniformity and plot frequency versus wave vectors to obtain (PD) curve from this model. The curve is measure up with inelastic neutron scattering technique. There exists a total of twelve external phonon modes; out of which nine branches are of optical phonons and rest three branches are acoustic phonons in Fig.2. The discontinuity in the spectrum, the number of branches of phonons existing under this discontinuity and the small dispersion overhead of this discontinuity is valid experimental evidence to distinguish the internal and external modes of the phonons of the Naphthalene crystal. Out of the three branches of the acoustic phonons, the one with the greatest slope belongs to the category of acoustic phonons which are longitudinal and the other two branches belong to the category of acoustic phonons which are transverse. In Fig.3 dispersion relation of the phonons is used to study the vibrational properties of a crystal lattice. The total energy of vibration of the crystal is given as the sum of discrete phonon energies. For naphthalene consisting of a minimum of two atoms in the unit cell, the scattering relation gives two kinds of phonon modes. The steep axis corresponds to the phonon frequency and the other axis corresponds to the vector of the wave and denotes the borderline of the first Brillouin zone. A crystal consisting of more than two atoms in the unit cell show three modes of acoustic phonons; out of which two phonon modes are transverse and the remaining one is longitudinal. For higher values of wavelength, the scattering relation is approximately free of the frequency of phonons and the rate of motion of the phonons is given because of this group of phonons with separate wavelengths can move inside the lattice for longer distances.

Figure 2: Combined density of States. Click here to View figure

Figure 3: Dispersion relation Curve. Click here to View figure

Conclusion

The computed value is approximately close to the experimental values. Hence, we analysed the lattice dynamics of naphthalene and thus got an idea of the speciality of this organic crystal. It is becoming evident that the semiconducting characteristics of organic crystals is growing fast and thereby widening its applicability research uses the present model in theoretical calculation of different types of crystal is also used ^13-15. Technological applications of these organic crystals are developing day by day. The property of production of luminescence electrically by polymers and small molecular mass steam discharge organic coverings are already into technical application. Researchers are concentrating on the launch of these flexible, low cost and lightweight materials in the electronic devices ranging from light emitting diodes to sensors for reception and detection applications.

Acknowledgement

I pay my tribute to my Ph.D. supervisor Late Prof. Dr. K S Upadhyaya Sir, for their guidance and continuous support.

Conflict of interest

There are no conflict of interest.

Funding Sources

Funding facility is not given by any agencies.

References

1. Dumas.G.; Chedin , M.P.; Vovelle, F. Journal de Physique, 1980, 41 ,905.
   CrossRef
2. Yang .X.; Xiao .L. P. Materials Science Forum., 2018,V 914,175 .
   CrossRef
3. Cai.W.; Yip. J. Li.; Massachusetts.S, Institute of Technology Cambridge, 2012,V1, 249.
   CrossRef
4. Bokhenkov, E.L.; Natkaniec.I.; Sheka, E.F,Institute of Solid State Physics, USSR, Academy of Sciences, 2014,111 (49), 17402.
5. Drickamer, H.G.; Science, 1967,156, 1183.
   CrossRef
6. Schellekens, J.M.T.; Phonons and electron phonon coupling in naphthalene (Ph.D.) Thesis, Eindhoven University of Technology,2001.
7. Robertson, J. Monteath.; Proc. R. Soc. Lond, 1933, A 142.
8. Mitra, S.S.; Bernstein, H.J .;Canadian Journal of Chemistry, 1959,V37.
9. Bougeard, D., Croatica Chemica Acta, 1988,61,243.
10. Afanas’eva,G.K., Sov. Phys. -Crystallogr. 1969,13, 892.
11. Verma, M.P.; Singh,R.K., Phys. Stat. Sol., 1969,33,769, 1969,36, 335, 1970,38, 851.
    CrossRef
12. Sakake,U.K.; Jha, P.K.; Sanyal, S.P, Bull. Mat. Science, 23:333, (2000).
    CrossRef
13. Srivastava,U.C.; Optoelectronics and Advanced Materials, Rapid Communications (OAM-RC), 2013,V7,9,698.
14. Srivastava, U.C.; International Journal of Modern Physics B, 2016,30, 1750020.
    CrossRef
15. Srivastava, U.C.; Johnson Matthey Technol. Rev., 2021,65, (1), 87.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.