Vibrational Frequencies of Oxygen Difluoride Using Lie Algebraic Model

Introduction

Analysis of vibrational specta of small-size molecules is among the most challenging aspects of current studies in molecular physics. The emergence of novel experimental techniques to produce vibrational spectra of molecules in higher overtones, requires reliable theoretical models for their interpretation. In this paper we are concerned with the vibrational spectra of oxygen difluoride using Lie algebraic approach. In this model, vibrational Hamiltonian matrix describes the vibrational energies of the molecule. In 1991, one-dimesional Lie algebraic method applied for the study of vibrational frequencies of small size molecules by Iachello and co-researchers ^{1, 2} and then this method was subsequently improved in vibrational spectra of medium-size molecules ^3-10.

Lie algebraic method ^{11, 12}

The general Hamiltonian for n vibrational modes of oxygen difluoride (F-O and F-O) is

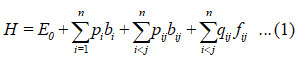
According to equation (1), b₁ and b₂ are invariant operators for uncoupled and coupled bonds respectively and are known as

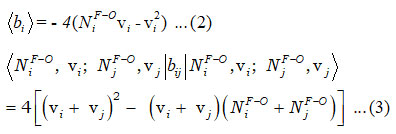
and the Majorana operator ƒ_ij is used to express the local mode interactions in pairs and contains non-diagonal and diagonal matrix elements,

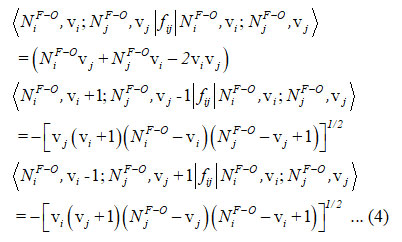
Hamiltonian for two stretching vibrations of oxygen difluoride molecule with C_2v symmetry point group can be written as

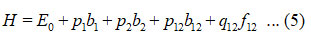
(cm^– In equation (5), p₁ , p₂ , p₁₂ and q₁₂ ¹), are algebraic parameters (cm^-1), estimated from the spectroscopic data. Two bonds (F-O) are equivalent in the oxygen difluoride; so, we consider as p₁ = p₂ = p, N₁^F‒O = N₂^F‒O = N^F‒O in equations (2), (3) and (4).

The Hamiltonian matrix for the first two local oscillators is

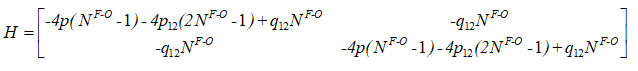
Results and Discussion

The energy equation (6) is used to find the initial value of the parameter p,

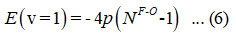
and the value for q₁₂ determined from the relation,

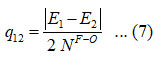
Where, E₁, E₂ are the oxygen difluoride, symmetric and antisymmetric vibrational frequencies, respectively. The oxygen difluoride vibrational frequencies were calculated using the Lie algebraic approach and the obtained results reported in (2) and table (3). The dimensionless Vibron number N₁ for stretching and bending bonds of oxygen difluoride is determined using the following relation,

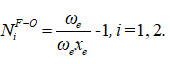
Where, ω_e (= 1053.0138), ω_e x_e (=9.9194) are the vibrational harmonic and anharmonic (spectroscopic) constants, respectively for the bond F-O ¹³

Table 1: Algebraic parameters

NF-O (stretching)	106
NO-F-O (bending)	62
p(stretching)	-2.0940
p(bending)	-1.8893
p12(stretching)	0.0574
p12(bending)	0.4685
q12(stretching)	0.4575
q12(bending)	3.7177

Table 2: Fundamental vibrational frequencies (in cm^-1)

Vibrational Mode	Symmetry	Observed [14]	Calculated
v1 (symmetric stretch)	A1	928	928.0244
v2 (bend)	A1	461	459.8062
v3 (antisymmetric stretch)	B1	831	831.0344

 

Table 3: Higher overtone vibrational frequencies (in cm^-1)

Overtone	Vibrational mode
	symmetric stretch (A1)	bend (A1)	antisymmetric stretch  (B1)
1	2v1 (1847.133 )	2v2 (906.247)	2v3 (1632.923)
2	3v1 (2743.971)	3v2 (1357.693)	3v3 (2427.607)
3	4v1 (3694.012)	4v2 (1794.012)	4v3 (3287.437)
4	5v1 (4571.063)	5v2 (2269.624)	5v3 (4071.773)
5	6v1(5513.453)	6v2(2683.483)	6v3(4870.003)
6	7v1(6384.138)	7v2(3172.896)	7v3(5783.896)
7	8v1(7353.148)	8v2(3523.312)	8v3(6561.324)
8	9v1(8208.200)	9v2(4004.915)	9v3(7318.005)

 

Table 4: Combinational bands (in cm^-1)

Combinational band	Calculated	Combinational band	Calculated
v1 + v2	1389.933	2v1 + v2	2309.042
v1 + v3	1759.518	v2 + 2v2	1369.801
v2 + v3	1292.943	v2 + 2v3	2094.832
v1 + 2v1	2775.616	2v1 + v3	2678.626
v1 + 2v2	1836.374	v3 + 2v2	1739.384
v1 + 2v3	2561.406	v3 + 2v3	2464.416

 

Conclusion

In the table (2), the estimated fundamental vibrational frequencies were compared with the observed data. In table (3) and (4), vibrational frequencies upto the nineth harmonic and combinational bands upto third harmonic reported accordingly by the Lie algebraic method.

Conflict of Interest

There is no conflict of interest.

Funding Sources

There is no funding source.

References

1. F. Iachello, S. Oss, R. Lemus, J. Mol. Spectrosc., 1991, 149 (1), 132-151. doi: 10.1016/00222852(91)90148-4
   CrossRef
2. Iachello, F.; Oss S. J. Mol. Spectrosc. 1991, 146, 56-78. doi: 10.1016/0022-2852(91)90370-P
   CrossRef
3. F. Iachello, S. Oss, J. Mol. Spectrosc.,  1992, 153 (1–2), 225-239. doi: 10.1016/0022- 2852(92)90471-Y
   CrossRef
4. A. Frank, R. Lemus, R. Bijker, F. Péilez Bernal, J.M. Arias, Ann. Physics, 1996, 252, 211-238.
   CrossRef
5. Zhaochi Feng, Guang Xiong, Qihua Yang, Qin Xin & Can Li, Chin Sci Bull, 1999, 44, 1961–1964. doi:10.1007/BF02887118
   CrossRef
6. V. Jaliparthi, M. Rao Balla, Spectrochim. Acta A, 2022, 264, 120289(1-8). doi:10.1016/j.saa.2021.120289
   CrossRef
7. M. R. Balla, S. Venigalla, V. Jaliparthi, Acta Phys. Pol. A , 2021, 140 (2), 138-140. doi: 10.12693/APhysPolA.140.138
   CrossRef
8. M. R. Balla, V. S. Jaliparthi, Polycyclic Aromatic Compounds , 2021. doi: 10.1080/10406638.2021.1901126.
   CrossRef
9. M. R. Balla, V. S. Jaliparthi, Mol. Phys., 2021, 115 (5), e1828634. doi.org/10.1080/00268976.2020.1828634
   CrossRef
10.  J. Vijayasekhar, K. A. Kumar, N. Srinivas, Orient J Chem 2021, 37(6).
    CrossRef
11. Iachello, F.; Levine, R. D. Oxford University Press, Oxford. 1995.
12. Oss, S. Adv. Chem. Phys.1996, 93, 455-649.
13. Irikura, K.K. J. Phys. Chem. Ref. Data., 2007, 36(2), 389-398.
    CrossRef
14. Shimanouchi, T, Tables of Molecular Vibrational Frequencies Consolidated Volume I, National Bureau of Standards, 1972.
    CrossRef

---

This work is licensed under a Creative Commons Attribution 4.0 International License.