Influence of Temperature on the Rheological Behavior of Orange Honey

Introduction

Honey is a natural product, consumed as food since ancient times [¹]. The special status of honey for consumers is due to its natural product image and health benefits ^[2,3]. After some scandals over honey, its quality by origin has become associated with consumer expectations. For example, in the European Community, counterfeit Chinese honey with high fructose corn syrup has been found, with other incidents involving the discovery of an excessive residue of antibiotic residue in honey from third world countries ^[4] . Therefore, quality standards emphasize the importance of honey quality by origin, and this is used in promoting sales through specific labeling. Labels such as monoflora or polyflora, organic, with a protected designation of origin, meet the requirements of the consumer, as well as those of the honey industry and control bodies. In addition, researchers are required to provide methods and markers that link honey to existing regulations.

The specifications of honey with geographical indication are generally based on physico-chemical parameters. These indicators have been shown to have limited potential in determining the origin of honey. Consequently, the discovery of chemical markers to help determine the quality of honey by origin, has been the subject of many studies in recent times. This includes studies dealing with volatile compounds [5], phenolic compounds [6] and the mineral content [7] of honey of different floral and geographical origins. The most recent and comprehensive study of this kind is the one written by Kaskoniene et al., 2010, [8] study that provides excellent results trying to define typical compounds that are best associated with the origin of honey. Within the Trace project, natural markers of honey, such as minerals [9], the ratio of (bio) isotopes and genetic markers were determined to determine the geographical, botanical and production origin [10-16]. This article presents ln n versus 1/T on the rheological behavior of orange honey. Honey was studied in the temperature range 25-45⁰C and humidity of 16%, 17%, 19% and 21%.

Material and methods

The orange honey studied in this article comes from Greece.  A study was performed to determine the effect of shear rates (3.3 to 120 s – 1) on shear stresses for orange honey at temperatures between (25 to 45°C). The absolute viscosities of the orange honey were determined using a Haake VT 550 viscometer, a rotary viscometer with coaxial cylinder HV₁ [17].

Results and discussion

Often, in technological processes, in order to improve the flow characteristics so as to facilitate the pumping, mixing, filling of containers, higher temperatures are used for the processed fluids. In liquids, viscosity is controlled by molecular cohesion forces and therefore the mobility of molecules increases by reducing the intensity of intermolecular forces, which explains the decrease in viscosity as the temperature increases. Hence the importance of strict temperature control when measuring viscosity or dependence .

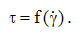
It is the viscosity dependent on temperature and can be substantial, the change being up to 10% /°C. The expression of Arrhenius equation:

In this expression E_a (J. K^-1mol^-1) represents the activation energy for viscosity, A (Pa. S) is a proportionality factor, R – universal gas constant, T(K) – absolute temperature, η (Pa ^. s) – viscosity Newtonian fluid.

Because the activation energy, E_a, is the energy barrier that must be overcome for flow to occur, this parameter can be correlated with the association of liquid molecules. A high value for the activation energy suggests a strong association, as well as the fact that a large amount of energy is required to achieve the dissociation necessary to initiate the flow.

Parameter A having the unit of measurement of viscosity should represent a viscosity. Theoretically, it would be the viscosity reached by the product at infinite temperature. But as this is not feasible, it was agreed that A is only a factor of proportionality.

By logarithm, relation (1) can be linearized:

Written in this form, mathematically addictive In

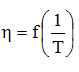
is a right in which ln A is found at the intersection with the ordinate, and

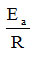
 it is the very slope of the right.

Therefore, the graphical representation of this dependence allows the graphical determination of the two parameters A and Ea, from the intersection with the ordinate, respectively from the slope of the line. Obviously, the two parameters ln A and

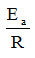
 they can also be calculated by linear regression.

If a slight curvature (concavity) occurs near the ordinate, this suggests that there are strong secondary bonds in Newtonian fluid. In this situation, only the temperature range in which the curve is linear is chosen, and the value pairs A and Ea are associated with this temperature range. It is thus possible to predict the viscosity of a Newtonian fluid at any temperature in the linear range of the dependence In

.

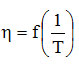
If we write the equation (1) for two decks, one of reference, for which the values of viscosity n_r at the reference temperature T_r are known, as well as for the unknown value of viscosity n_x at temperature T_x, by dividing the two expressions we eliminate ln A, and by logarithm the expression is obtained that allows the calculation of the viscosity n_x:

Using this relationship involves knowing the value of the activation energy for the Newtonian fluid studied.

The influence of temperature on an assortment of honey obtained from orange blossoms at different unit contents is presented in the following graphs [18]. For the calculation of the parameters A and E_a we graphically represented the logarithm of the viscosity values and the inverse of the temperatures (expressed as absolute temperatures) and we obtained the pairs of points that allowed the graphical representation of the dependence

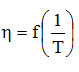
Figure 1:  Linearization ln versus 1/T of an orange honey assortment, with a moisture content of 16% for the temperature range 25-45°C Click here to View figure

Figure 2: Linearization ln versus 1/T of an assortment of honey from oranges, with a moisture content of 17% for the temperature. Click here to View figure

Figure 3:  Linearization ln versus 1/T of an assortment of honey from oranges, with a moisture content of 19% for the temperature range 25-45°C Click here to View figure

Figure 4:  Linearization ln versus 1/T  of an assortment of honey from oranges, with a moisture content of 21% for the temperature range 25-45°C Click here to View figure

By the linear regression applied to the lines 1, 2, 3 and 4, it was possible to obtain the values for ln A at the intersection of the linear regression line with the ordinate,

respectively for

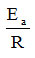
from the slope of the regression line. By cologaritmare the value of A is calculated, and from the product of the slope with the value of the universal gas constant (R) the value of the activation energy E_a is calculated. The obtained results are presented in table 1. It is observed from the table that the values of the two parameters A and Ea are influenced by the moisture content of the honey.

Table 1:  Values obtained by nonlinear regression for parameters A and E_a in the case of an assortment of honey from potrocale at different moisture contents, for the temperature range 25-45°C

Moisture content (%)	Ea (kJ . mol-1)	A (Pa . s)	R
15.9	89.94	3.03 . 10-15	0.9992
17.0	84.76	1.42 . 10-14	0.9990
19.0	78.90	7.89 . 10-14	0.9988
21.0	73.17	4.56 . 10-13	0.9981

 

In the case of non-Newtonian fluids, temperature is expected to influence their flow behavior. In the case of pseudoplastic fluids, the temperature influences the value of the consistency coefficient K, but its influence on the behavior index n is insignificant. This means that by heating or cooling, if no fluid transformations occur, the pseudoplast character does not change.

Because in non-Newtonian fluids the apparent viscosity is also influenced by the shear rate, the effects of temperature and shear rate have been combined in a single expression [17-24]:

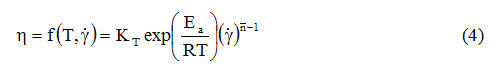
As in expression (1), and in expression (4) K_T is a proportionality factor, even if it has the unit of measurement of the consistency coefficient (Pa. Sⁿ). By amplifying the relation (4) with the shear speed, the influence of the temperature on the shear stress will be obtained:

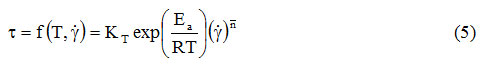
From these two relations it can be seen that even in the case of the consistency coefficient the temperature has a logarithmic influence, of the form:

Conclusions

The effect of ln versus 1/T of honey showed that the viscosity of honey decreases with increasing temperature and best modeled with the Arrhenius equation. This article presents influence temperature on the rheological behavior of orange honey whose viscosity increases with increasing temperature. Honey was studied in the temperature range 25-45⁰C and humidity of 16%, 17%, 19% and 21%.

The rheological behavior is influenced by both humidity and its composition. The activation energy decreases with increasing unity in a similar way to the correlation coefficient.

References

1. Ransome, 2004. The sacred bee in ancient times and folklore. London: Courier Dover Publications, Dover Books on Antropology and Folklore
2. Mărghitaş L., 2008. Albinele şi produsele lor, Editura Ceres, Bucureşti
3. Bura M., Pătruică D., Bura V.A., 2005. Tehnologie apicolă, Editura Solness.
4. Ochi T., 2005. American Bee Journal, 145(12), 937-938.
5. Cuevas-Glory L.F., Pino J.A., Santiago L.S., Sauri-Duch E., 2007,  Food Chemistry, 103(3), 1032-1043.
   CrossRef
6. Pyrzynska I., Biesaga M., 2009, Trac-Trends in Analitical Chemistry, 28(7), 893-902.
   CrossRef
7. Pohl P., 2009, Trac-Trends in Analitical Chemistry, 28(1), 117-128.
   CrossRef
8. Kaskoniene V., Venskutonis P.R., 2010, Comprehensive Review of Food Science and Food Safety, 9(6), 620-634.
   CrossRef
9. Vanhanen L.P., Emmertz A., Savage G.P., 2011, Food Chemistry, 128(1), 236-240.
   CrossRef
10. Aliferis K.A., Tarantilis P.A., Harizanis P.C., Alissandrakis E., 2010, Food Chemistry, 121(3), 856-862.
    CrossRef
11. Beretta G., Caneva E., Facino R.M., 2007, Planta Medica, 73(15), 1592-1595.
    CrossRef
12. Terrab A., Pontes A., Heredia F.J., Diez M.J., 2004, Grana, 43, 116-121. CrossRef
13. Tuberoso C.I.G., Bifulco E., Caboni P., Cottiglia F., Cabras P., Floris I., 2010,Journal of Agricultural and Food Chemistry, 58(1), 384-389.
    CrossRef
14. Fernández Pierna J.A., Abbas O., Dardenne P., Baeten V., 2011,  Biotechnological Agronomic Society, 15(1), 75-84.
15. Woodcock T., Downey G., Kelly J.D., O’Donnell C., 2007, Journal of Agriculture and Food Chemistry, 55(22), 9128-9134.
    CrossRef
16. Karoui R., Dufour E., Bosset J.O., De Baerdemaeker J., 2007, Food Chemistry, 101(1), 314-323.
    CrossRef
17. Steffe, J.F. 1996. Rheological Methods in Food Process Engineering, Ediţia a 2-a, Freeman Press, 2807 Still Vallez Dr., East Lansing, MI 48823, USA
18. Yanniotis S., Skaltsi S., Karaburnioti S. 2006,  J. Food Engineering 72, 372–377
    CrossRef
19. Stanciu I.,  2015, Oriental Journal of Chemistry, 31(3), 1383-1387.
    CrossRef
20. Stanciu I., 2015, Oriental Journal of Chemistry, 31(4), 2017-2023.
    CrossRef
21. Stanciu I, Ouerfelli N., 2020,  Journal of Biochemical Technology, 3(11), 52-57.
22. Stanciu I., Messaâdi A., Díez-Sales  O.,  Al-Jameel  S.S.,  Mliki  E., Herráez  J.V.,  Ouerfelli  N., 2020,  Journal of Biochemical Technology, 3(11),  102-114.
23. Stanciu I., Journal of Science and Arts, 2018, 2(43), pp. 453-458
24. Stanciu I., 2012, Analele Universitatii “Ovidius” Constanta – Seria Chimie, 23(1), 27-30.
    CrossRef

---

This work is licensed under a Creative Commons Attribution 4.0 International License.