Optical Parameters of Amorphous Ge-Te-Se Films from Ellipsometric Measurements

Introduction

Chalcogenide semiconducting glasses have an interesting optical properties. These properties include high linear, nonlinear refractive index, broad infrared transparency and low photon energies [1]. Accordingly, many technological applications emerges, including data storage, fiber optics, memory devices, flexible phase change and other optoelectronic applications [2 -6].

To the author knowledge, most of optical investigations are carried out by spectrophotometer technique (ST). The data obtained by ST usually analyzed by means of Swanpole method [7, 8]. The Swanpole’s method is frequently used in connection with Cauchy equation [9]. The Cauchy equation itself is an experimental formula which recounts the refractive index to the photon energy through some factors that have physical meaningless. Moreover, this equation cannot be considered as Kramers-Kroning (KK) consistent. It should be mentioned that in the KK consistent models, the refractive index cannot be estimated without the extinction coefficient value is identified.

Alternatively, spectroscopic ellipsometry (SE) emerges as effective tools for examining the optical properties of films. The ellipsometric devices are rapid, nondestructive tools. Moreover it is actual subtle to the occurrence of surface sheets and it grip advanced precision for resolving of the optical properties and thickness of thin film in contrast to the spectrophotometric technique [10, 11]. To acquire precise factors from SE, choosing a suitable dispersion model is essential. For amorphous materials Tauc–Lorentz (TL) and Cody–Lorentz (CL) models, which are KK consistent, are proper for inspecting SE results [12-15].

Selenium and tellurium are used in several electronic applications. Although telluride based glassy compositions deal as IR transmission and display optical phase recording, the glass forming ability is very low. Similarly, selenium is a proper glass former but shows low glass stability. Therefore, Se-Te alloys has been exposed to be improved properties in terms of crystallization, transmittance, hardness, ageing, than the pure form of Se and Te. [16-27]. Se-Te -based chalcogenide glasses is supposed to be a stimulating glass due to its important applications nevertheless, it has low sensitivity and small lifetime consequently numerous researchers have engaged definite additives such as Ge, Bi and Sn. The adding of the third element might increase thermal stability, generate topological and chemical disorder in Te–Se alloys[28, 29].

The addition of Ge to Se-Te medium overwhelms the disadvantages of the binary Se-Te alloy. Ge cross-links with the Se chain alter the bonds, then enhances the glass formation region. Furthermore, the size and the electronegativity of Ge-Se-Te medium elements are well-matched and therefore, outcomes in high-quality established melts [30, 31]. In this work, the optical parameters of the prepared thin films of Se₁₅Te_62.5Ge_22.5 and Se₁₀Te_67.5Ge_22.5 were obtained using variable angle spectroscopic ellipsometry (VASE) method. Furthermore, summation of a number of dispersion equations were employed to designate the optical parameters over the measured spectral range.

Theory

Spectroscopic Ellipsometry (SE) treaties with the variation light polarization that is reflected or transmitted through a film. The polarization variation is designated by phase difference (Δ) and amplitude ratio, (Ψ), between light concerned with in the p- and s- directions relative to the film surface:

where r_s and r_p characterize the complex Fresnel quantities for p- and s- polarizations, respectively. A common relation between the SE results (Ψ,Δ) and a (real and imaginary) dielectric function [10] is following formula:

where Φ_a is the incident light angle and ε_a (≈ 1) is the dielectric function of the ambient. It should be mentioned that the refractive (n) index and extinction coefficient (k) can be obtained from the real and imaginary part of the dielectric function via the subsequent relations

The values of absorption coefficient α (E) and normal- incident reflectivity R(E) of the films can be obtained by

Experimental

Glasses of the Se₁₅Te_62.5Ge_22.5 and Se₁₀Te_67.5Ge_22.5 were fabricated as bulk using the melt-quenching method. Elements (Se, Te and Ge) with purity (5N) were used to produce the bulk glasses. The total weight of mixture for both samples was 8 gm and placed in silica tubes and the tubes were evacuated of the order of 10^-5 Torr. Then the tubes were transferred into a furnace at 1000°C for 4 h through continuous shaking. The tubes were suddenly lay in cold water (at 0ºC) to produce bulk glass.

Thin films were arranged from the obtained bulk configurations using a thermal evaporation method. Ground bulk samples were evaporated from a molybdenum boat and deposited on BK7 glass substrates at room temperature. One evaporator source Edwards E306A have been employed at pressure <10^-6 Torr.

Optical functions were measured via Woollam Variable Angle Spectroscopic Ellipsometer (VASE) system. Measured quantities were obtained in the range of wavelength from 245nm to 1500 nm, at 55º, 65º and 75ºangle of incidence at room temperature. The accrued data from VASE was analyzed using the WVASE32 software [32]. In the current investigation, merely the mean squared error (MSE) is employed as reference to validate the variance between the experimental data and the model anticipated results. The lowest MSE’s value the superior correct is acquired. The dielectric data is explained by a summation of optical dispersion oscillators.

Results and Discussion

The X-ray diffraction (XRD) technique was employed in order to examine the amorphous nature of Se₁₅Te_62.5Ge_22.5 and Se₁₀Te_67.5Ge_22.5. films. Note that the occurrence of peaks on XRD pattern are denoted to incident beam reflection from the lattice planes. Fig. 1 displays the XRD pattern of as-deposited Se₁₅Te_62.5Ge_22.5 and Se₁₀Te_67.5Ge_22.5 films. The nonappearance of peaks for present samples approves the non-crystalline nature of the films.

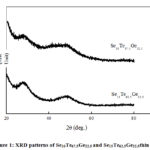Figure 1: XRD patterns of Se10Te67.5Ge22.5 and Se15Te62.5Ge22.5thin films. Click here to View Figure

Figs. 2 and 3 characterizes the VASE results of Ψ and Δ (open circles) for Se₁₅Te_62.5Ge_22.5 and Se₁₀Te_67.5Ge_22.5. thin films, respectively. The results designate almost entirely absorbed incident light on the films in the range of wavelengths below 715 nm and 773 nm for Se₁₅Te_62.5Ge_22.5 and Se₁₀Te_67.5Ge_22.5, respectively. Transmission is found to be occurs beyond the stated wavelengths where typical fluctuation occurs in the Ψ and Δ Curves.

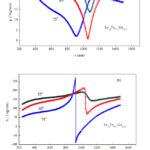Figure 2: (a, b) VASE data points (open circles) and modeled (solid curves) Click here to View Figure

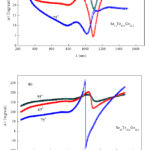Figure 3: (a, b) VASE data points (open circles) and modeled (solid curves) Click here to View Figure

The experimental data of the dielectric function spectra (ε₁ and ε₂) represented in Figs 4 and 5 of an as-deposited Se₁₅Te_62.5Ge_22.5 and Se₁₀Te_67.5Ge_22.5 thin films, respectively. The data is shown as open circles. It can be noted from these figures that both ε₁ and ε₂ spectrum are composed from number of dissimilar wide peaks. This characterization of ε₁ and ε₂ spectrum is tough to appropriate by single desperation model. Accordingly it appearances to be sensible to designate the dielectric function of the current films by mixture of several oscillator functions.

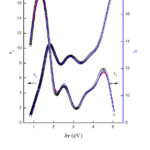Figure 4: Validation of model fits to measured dielectric function data Click here to View Figure

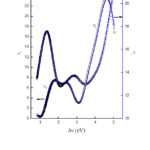Figure 5: Validation of model fits to measured dielectric function data Click here to View Figure

It should be mentioned that the imaginary part of the dielectric function, ε₂, is assumed to be as the multiplying variable band edge function by Lorentz oscillator. The variable band edge functions for semiconductors were proposed by Tauc–Lorentz (TL) [12, 13] and Cody–Lorentz (CL) [14, 15] were exposed to be proper to account of optical responses in disordered semiconductors. The expression of the ε₂, according to TL given as:

where, E₀,and E_g are the peak transition energy and optical band gap energy. On the other hand A, and C are Amplitude and width of Lorentz oscillator. However, for CL model is given as

where E_t, is a change energy between the band-to-band and Urbach tail transitions, E_u signifies the range of enlargement and E_p an alteration energy that splits the absorption beginning manners from the Lorentzian manners.

The summation of dispersion functions employed at this point contain one TL function with several Gaussian -formed functions or one CL function with several Gaussian -formed functions. Above statement can be expressed as follows.

The eqs. 11 and 12 will be denoted as TL-group and CL-group, respectively. In Figs. 4 and 5, the data point of imaginary and real parts of dielectric functions of Se₁₅Te_62.5Ge_22.5 and Se₁₀Te_67.5Ge_22.5 were fit by means of grouping of one TL (CL) and three Gaussian functions. It can be noted that the TL and CL oscillators functions were active to fit the essential band gap whereas the Gaussian functions were working to represent the molecular and lattice vibrations or in the infrared and ultraviolet sections.

In Figs.4 and 5, the dashed and solid curves signifies fitting via TL-group and CL-group. It is clear from these figures that a plausible fitting between experimental data and constricted oscillators group for dielectric function acquired for the two groups labeled beforehand. The surface roughness and thicknesses of the Films are the same for the TL and CL group. The oscillators parameters for as-prepared Se₁₅Te_62.5Ge_22.5 and Se₁₀Te_67.5Ge_22.5 films by both groups are given in Table 1.

When the model fits the experimental results as closely as possible, the value of MSE displays a minimum value. We note from Table I that the values of MSE CL- group for the two films are sound and lesser than its corresponding of TL-group. Therefore, we can consider CL- group as more appropriate to model the present films than TL- group. The data measured by SE is fairly sensitive to surface constructions thus it should be combine surface roughness in the data analysis optical model. The effective medium approximation (EMA) fairly represent surface roughness. In examining surface roughness using EMA, it is essential that the surface roughness be fewer than λ /10 of the wavelength.

The resulting fit to pesodielectric functions using the preceding oscillators groups leads to fits Δ and Ψ. The solid curves in Figs.2 and 3 signify the fitting using CL group. It would be stated that the linear summation from some equations have been employed with obvious productively to fit the dielectric spectra for some amorphous films [33-35].

For industrial functions, the extinction coefficient (k) and the refractive index (n) obtained by the above mentioned analysis of VASE data are greatly important. The wavelength dependence of n and k for the as-prepared Se₁₅Te_62.5Ge_22.5 and Se₁₀Te_67.5Ge_22.5 thin films be present in Figs. 6 and 7. It should be mentioned that the Cauchy equation could be designated optical functions in the transparent region properly. For the present samples, simple Cauchy model can be only suitable for wavelength above 850 and 920 nm for Se₁₅Te_62.5Ge_22.5 and Se₁₀Te_67.5Ge_22.5, respectively. The estimated values of the absorption coefficient typically to CL group as a function of photon energy for Se₁₀Te_67.5Ge_22.5 and Se₁₅Te_62.5Ge_22.5films are shown in Fig. 8. Similar behavior can be noted in the onset absorption edge.

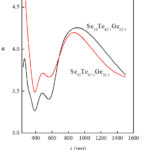Figure 6: Refractive index (n) as function in wavelength (l)  Click here to View Figure

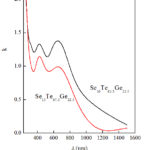Figure 7: Extension coefficient (k) as function in wavelength Click here to View Figure

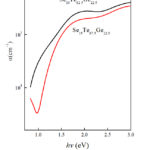Figure 8: Variation of the estimated value of absorption coefficient based on Click here to View Figure

The essential energy gap E_g of the films can be also estimated from the variation of the absorption coefficient with the incident photon energy (hv) using the relation [36]

where B is an energy independent constant and r is an exponent which can be expected to have several values depend on the origin of electronic shift. For amorphous semiconductors, the exponent r is equal 2. Fig. 9 displays the variation of (ahv)^1/2 with photon energy for as-prepared Se₁₅Te_62.5Ge_22.5 and Se₁₀Te_67.5Ge_22.5 films. The essential energy gap E_g can be achieved from the intercept of the prolonged straight lines with the hv axes i.e, (ahv)^1/2 =0. Both E_g and constant B estimated and found to be 0.95 eV and 6.64 x10² cm^-1eV^-1 for Se₁₅Te_62.5Ge_22.5 however for Se₁₀Te_67.5Ge_22.5 are 0.62 eV and 4.63 x10² cm^-1eV^-1.

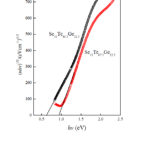Figure 9: Absorption coefficient plotted as (αhv)1/2 against photon energy Click here to View Figure

Conclusion

In conclusion, we investigate the optical parameters of Se₁₅Te_62.5Ge_22.5 Se₁₀Te_67.5Ge_22.5 using variable angle spectroscopic ellipsometry. The films were prepared using thermal evaporation method. The outcomes described in present paper showed that the amorphous nature of the prepared films that was confirmed through X-ray diffraction. To fit the ellipsometry data linear summation from Cody-Lorentz (Tacu- Lorentz) with further Gaussian oscillators were employed to calculate the optical parameters. It was found that the values of band gap energy 0.95 eV and 0.62 eV for Se₁₅Te_62.5Ge_22.5 and Se₁₀Te_67.5Ge_22.5, respectively.

Acknowledgements

This study was funded by the Deanship of Scientific Research, Taif University, KSA [research project number 1-438-5991].

References

1. Seddon, A.B. Non-Cryst. Solids. , 1995, 184, 44-50.
   CrossRef
2. Nermec, P.; Frumar, M.; Jedelsky,J; Jelinek, M.; Lancok,J.; Gregora,I. Non-Cryst. Solids. , 2002, 302, 1013.
   CrossRef
3.  Kamboj, M.S.; Kaur, G.; Thangaraj, R. Thin Solid Films. , 2002, 350, 420.
   CrossRef
4.  Tanaka, K. Current Opinion in Solid State & Materials Science. , 1996, 1, 567.
   CrossRef
5. Zakery, A.; Elliott, S.R. Non-Cryst. Solids. , 2003, 330, 1–12.
   CrossRef
6. Kolobov, A.V, Photo-Induced Metastability in Amorphous Semiconductors,Wiley-VCH., 2003.
   CrossRef
7. Swanepoel, R. Phys. E: Sci. Instrum., 1983, 16, 12142.
   CrossRef
8. Swanepoel. R, Phys. E: Sci. Instrum., 1984, 17, 896.
   CrossRef
9. Abdel-Wahab, F.; Ali karar, N.N.; El Shaikh, H.A.; Salem, R.M. Physica B., 2013, 422, 40.
   CrossRef
10. Azzam, R.V.A.; Bashara, N.M. Ellipsometry and Polarized Light (North-Holland, Amsterdam, 1977). , 1977, p. 269.
    CrossRef
11. Ward, L. Appl. Phys., 1984, 17, 1781.
    CrossRef
12. Jellison, G. E. and Modine, F. A. Phys. Lett. ,1996, 69, 371
    CrossRef
13. Jellison, G. E and Modine, F. A. Phys. Lett. ,1996, 69, 2137.
    CrossRef
14. Cody, G. D. in Semiconductors and Semimetals. , 1984, 21B, 11.
    CrossRef
15. Ferlauto, A. S.; Ferreira, G. M.; Pearce, J. M.; Wronski, C. R.; Collins, R. W.; Deng. X. M.; Ganguly, G. Appl. Phys., 2002, 92, 2424.
    CrossRef
16. Ležal, D.; Kašik, J.; Gotz. J. Non-Cryst. Solids. , 1987, 90, 557.
    CrossRef
17. Trnovcova, V.; Pažurova, T.; Šramkova. T.; Ležal, D. Non-Cryst. Solids. , 1987, 90 561.
    CrossRef
18. Adam, J.L. Rev., 2002, 102, 2461.
    CrossRef
19. Zavadil, J.; Kostka, P.; Pedlikova, J.; Zdansky, K.; Kubliha, M.; Labas, V.; Kaluzny, J. Non-Crystalline Solids. , 2009, 355, 2083–2087.
    CrossRef
20. Xin Jiang, Animesh Jha, Sensors and Actuators B., 2015, 206, 159–169.
    CrossRef
21. Cheruvalath, A.; Sebastian, I.; Sebastian, M.; Nampoori, V.P.N.; Thomas, S. Optical Materials., 2017, 72, 265.
    CrossRef
22. Wang, G.; Nie, Q.; Wang, X.; Dai, S.; Xu, T.; Shen, X.; Zhang, X. Physica B., 2010, 405, 4424–4428.
    CrossRef
23. Kubliha, M.; Kostka. P.; Trnovcova, V.; Zavadil, J.; Bednarcik, J.; Labaš, V.; Pedlikova, J.; Dippel, A.;-Ch, Liermann. H.; Psota, J. All. Comp., 2014, 586, 308.
    CrossRef
24. Mohamed, M.; Abdel-Rahim, M.A. Sci. Semic. Proces. , 2014, 27, 288.
    CrossRef
25. Černošek, Z.; Černošková, E.; Hejdová, M.; Holubová, J.; Todorov, R. Journal of Non-Crystalline Solids. , 2017, 460, 169–177.
    CrossRef
26. Vinod, E.M.; Sangunni, K.S. Thin Solid Films. , 2014, 550, 569–574.
    CrossRef
27. Rao, V.; Mehta, N.; Dwivedi, D. Res. Innov., 2019, 23, 141-148.
    CrossRef
28. Abdel-Wahab, F. Physica B., 2011,406, 1053–1059.
    CrossRef
29. Wang, G.; Nie, Q.; Wang, X.; Dai, S.; Xu, T.; Shen, X.; Zhang, X. Physica B.,2010, 405, 4424.
    CrossRef
30. Yin, N.; Xu, J.; Chang, F.; Jian, Z.; Gao, C. Infrared Phys. Technol., 2019, 96, 361-365.
    CrossRef
31. Hosseinkhani, A.; Tavoosi, M.; Ghasemi, A. Infrared Phys. Technol., 2017,85, 421- 430.
    CrossRef
32. Guide to Using WVASE 32, J.A. Woollam Co., Inc., Lincoln NE.
    CrossRef
33. Abdel-Wahab, F.; Merazga, A.; Rasheedy, M.S.;  Montaser, A.A. Optik., 2016, 127, 3871.
    CrossRef
34. Abdel-Wahab,F.; Badawi, A.; Alatibi, M.S.; Alomairy, S.E.; Ashraf, I.M.; Ahmed, E.M. , 2017,147, 59.
    CrossRef
35. Abdel-Wahab, F.; Ashraf, I.M.; Alomairy, S.E. Physica B, . 2018,530, 300.
    CrossRef
36. Tauc, J. Tauc (Ed.), Amorphous and Liquid Semiconductors, Plenum, New York. , 1974, p. 159.
    CrossRef

---

This work is licensed under a Creative Commons Attribution 4.0 International License.