Correlation between Dynamic Viscosity and Temperature for Vegetable Oil

Introduction

Alternative equations of two constant, three constant and multi-constant forms were proposed by some researchers to describe the dependence of dynamic viscosity of liquids on temperature. Simple form of two constant was proposed by De Guzman and Abramovic [1,2]. Three-constant forms were used and proposed in Vogel study, Andrade study, Noureddini study and in Abramovic study [2-5].

Multi-constant forms were proposed in several studies by Thorpe [6], Noureddini [5] and Daubert.[5-7] A polynomial or exponential dependence between temperature and dynamic viscosity of vegetable oil were proposed in Stanciu study.[8]

The effect of temperature on dynamic viscosity of vegetable oil has been studied by several studies.[1-5, 8] These studies proposed two, three and multi-constant formula to describe this temperature dependence. Simple formulas of two-constant were proposed to describe the effect of temperature on dynamic viscosity. These are given by:

η =Ae^B/T                                                                      (1)

η =CT ^D                                                                     (2)

Where η is the dynamic viscosity in cP, T is the temperature in K, A and B are constants. [1,4, 9, 10]

Three-constant formulas were used to represent the dynamic viscosity as a function of temperature, which are:

ln η =A+B/T +C/T²                                                              (3)

  ln η =A+B/T +CT                                                              (4)

where η is the dynamic viscosity in Pa, s and T is the temperature in Kelvin. A, B, C and D are constants. [2,11-14]

These are represented in the following equations:

ln η = A + B/T +CT  + DT ²                                                 (5)

n η = A + BT +CT ² + DT ³                                                 (6)

Where η is the dynamic viscosity in Pa.s in equation(6) and in cP in equation (7). T is the temperature in Kelvin. A, B, C and D are constants [15-17,8, 9].

The objective of this article is to find a dependence relation of the dynamic viscosity as a function of temperature for the coconut oil. By fitting the experimental curves we found the relation (7) that shows the dependence of the dynamic viscosity as a function of temperature at all the shear speeds at which the oil was studied.

Material and methods

Types of coconut oil used in this paper are produced of Secom in Romania. The coconut oil studied at temperatures between 40 and 100⁰C and shear rates between 3 and 120 s^-1 using a Haake VT 550 Viscotester used with the HV₁ viscosity sensor (University of Bucharest). The accuracy of the temperature was ± 0.1^oC.

Results and Discussion

Figures 1-8 show the exponential decrease in dynamic viscosity with temperature at the shear rates at which the oil was studied.

Figure 1: Dependence dynamic viscosity versus temperature Click here to View Figure

Figure 2: Dependence dynamic viscosity versus temperature at shear rate 6s-1 Click here to View Figure

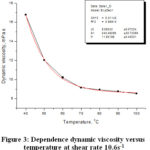Figure 3: Dependence dynamic viscosity versus temperature at shear rate 10.6s-1 Click here to View Figure

Figure 4: Dependence dynamic viscosity versus temperature at shear rate 17.87s-1 Click here to View Figure

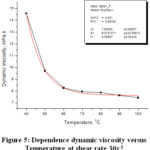Figure 5: Dependence dynamic viscosity versus Temperature at shear rate 30s-1 Click here to View Figure

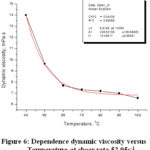Figure 6: Dependence dynamic viscosity versus Temperature at shear rate 52.95s-1 Click here to View Figure

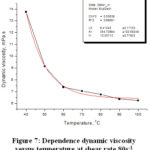Figure 7: Dependence dynamic viscosity versus temperature at shear rate 80s-1 Click here to View Figure

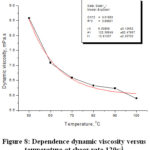Figure 8: Dependence dynamic viscosity versus temperature at shear rate 120s-1 Click here to View Figure

The program Origin 6.0 was used to determine constants for coconut oil.

The exponential dependence of the dynamic temperature viscosity is described by equation (7) which has the form:

η = η₀ +A e ^-t/B                                                                (7)

where η₀, A and  B they are constant and are different depending on the shear rate.

Parameters A, B and η₀ depend on the working conditions, the type of oil, and the shear speeds.

The values of the constants and η₀ , A and B and the correlation coefficients are included in Table 1.

Table 1: The value shear rate, value of parameters A and B of described by equation (7) and coefficient correlation R² for coconut oil

Valueshear rate, s-1	Value of parameters	Value of parameters	Value of parameters	Value correlation coefficient, R2
	η0	A	B
3.3	8.9812	153.1473	18.9844	0.9999
6	8.9799	172.7209	14.7205	0.9807
10.6	8.0799	95.1123	16.9476	0.9725
17.87	7.5877	80.5137	17.0566	0.9615
30	7.2580	131.8048	13.9522	0.9695
52.95	6.6084	149.8882	13.3417	0.9842
80	6.1921	156.7318	13.2341	0.9909
120	6.1180	1107.9796	8.6595	0.9888

The value of η₀ decreases with the increase of the shear speed and at high shear speeds the decrease is smaller between 6.6084 and 6.1180. Parameter A has a maximum value of 1107.9796 at the shear rate 120 s^-1 and a minimum value of 80.5137 at the shear rate 17.87 s^-1. Parameter B decreases with increasing shear speed and has a minimum value of 8.6595 at shear speed 120 s^-1. The correlation coefficients have values close to the unit with the lowest value being at the shear rate 17.87 s^-1 of 0.9615.

Conclusions

This article presents the study coconut oil at temperatures between 40 and 100⁰C. We found the exponential relation (7) of the dependence of the dynamic temperature viscosity at the shear rates between 3.3 s^-1 and 120 s^-1. The correlation coefficients have values close to the unit with the lowest value being at the shear rate 17.87 s^-1 of 0.9615.

References

1. De Guzman J., Anales; Soc. Espan. Fis. Y. Quim., 1913, 11, 353.
2. Abramovic H., Gklofutar; Acta. Slov., 1998, 45, 69.
3. Vogel H.; Physics., 1921, 22, 645.
4. Andrade C.; Nature, 1930, 125, 309.
5. Noureddini H., Teoh B., Clements L.; JAOCS, 1992, 69, 1189.
6. Thorpe T., Rodger J., Barnett R.; Part II, Phil.Trans., 1897, 189, 71.
7. Daubert T., Danner R.; Physical and thermodynamic properties of pure chemicals . data compilation design institute for Physical properties dataAIChE, Taylor and Francis,Washington DC (1989-1994).
8. Stanciu I.; J. Pet. Technol. Altern. Fuels., 2012, 3, 19-23.
9. Nierat T. H., Abdelraziq I. R., Materials Science an Indian Journal, 2015, 12(7), 257-262.
10. Natarajan G., Viswanath D.; Data Book on Viscosity of Liquids, Hemisphere, New York, 1989.
11. Neelamegam P., Krishnaraj S.; IJCT., 2011, 18, 463.
12. Nierat T., Mohammad Sh., Abdelraziq I.; J.Material Env. Sci., 2014, 5(1), 245.
13. Stanciu I.; Journal of Science and Arts 2018,  1(42), 197-202
14. Reid R., Prausnitzand J., Poling B.; Properties of Gases and Liquid, McGraw-Hill, New York, 4^th Edition, 1987.
15. Stanciu I.,  Oriental Journal of Chemistry, 2015, 31(3), 1383-1387.
16. Stanciu I., Oriental Journal of Chemistry, 2015, 31(4), 2017-2023.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.