Some Topological Indices and their Polynomials of Graphene

Introduction

Graphene is a nanomaterial. Recently Rajesh kanna and his students computed some of the  topological indices of Graphene^1,2. In this article, we have computed third Zagreb index, first Zagreb polynomial, second Zagreb polynomial, third Zagreb polynomial, hyper Zagreb index, forgotten index, symmetric division index. Also we have defined hyper Zagreb polynomial, forgotten polynomial and symmetric division polynomial of Graphene.

Third Zagreb Index

Fath-Tabar introduced the third Zagreb index, first, second and third Zagreb polynomial in 2011 as follows³.

Definition 1.1 For a simple connected graph G, the third Zagreb index is defined as,

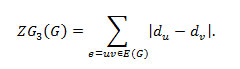
Definition 1.2: The First, Second and Third Zagreb Polynomials for a simple connected graph G is defined as,

Hyper Zagreb index

G.H. Shirdel et.al introduced a new distance-based Zagreb indices of a graph G named Hyper-Zagreb Index⁴.

Definition 1.3: The hyper Zagreb index is defined as,

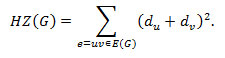
We define Hyper Zagreb polynomial as follows,

Definition 1.4: The hyper Zagreb polynomial is defined as,

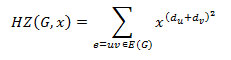
Forgotten index

Definition 1.5: The forgotten topological index is also a degree based topological index, denoted by F(G) for simple graph G. It was encountered in⁵ and defined as,

Definition 1.6: The forgotten polynomial for a graph G is defined as,

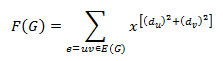
Symmetric division index

These topological indices are quite useful for determining total surface area and heat formation of some chemical compounds.

Definition 1.7: Symmetric division index is defined as

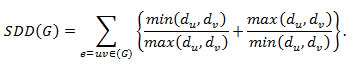
Further, we define symmetric division polynomial as follows

Definition 1.8: The Symmetric division polynomial is defined as

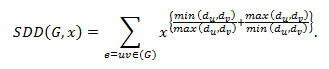
Main results

Theorem 2.1. The third Zagreb index of Graphene

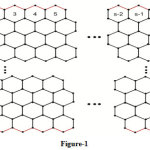Figure 1: where ‘t’ is the number of rows of benzene rings and ‘s’ is the number of benzene rings in each row. Click here to view figure

Proof

2D structure of Graphene is as shown in the above figure-1. Assume that it contains ‘t’ rows and  ‘s’ benzene rings in every row. The edge connecting the vertices of degree d_i and d_j  is denoted by m_i,j. Let |m_i,j|  denotes the number of edges of the type m_i,j.  In ² we can see that |m_2,2| = (t+4), |m_2,3|=(4s+2t-4)  and |m_3,3| = (3ts-2s-t-1).

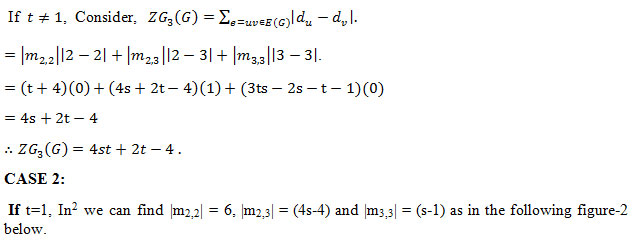
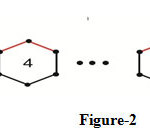Figure 2: t=1, In2 we can find |m2,2| = 6, |m2,3| = (4s-4) and |m3,3| = (s-1) as in the following figure. Click here to view figure

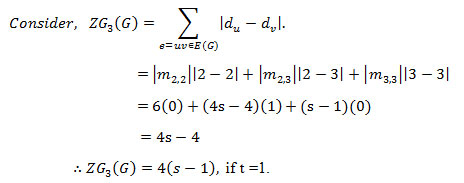
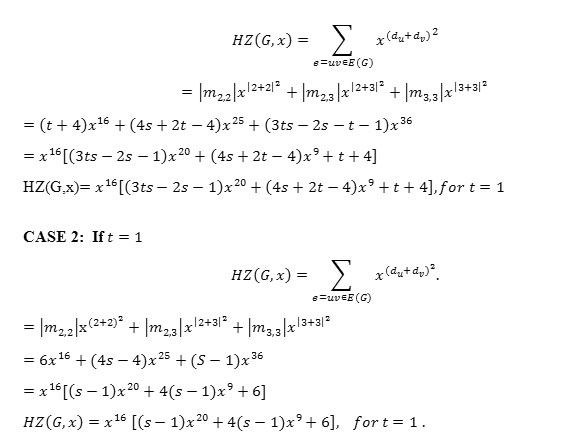
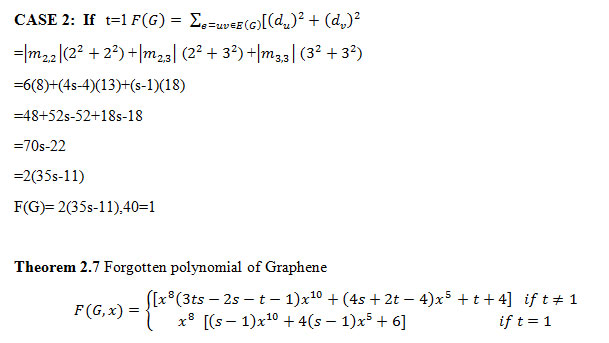
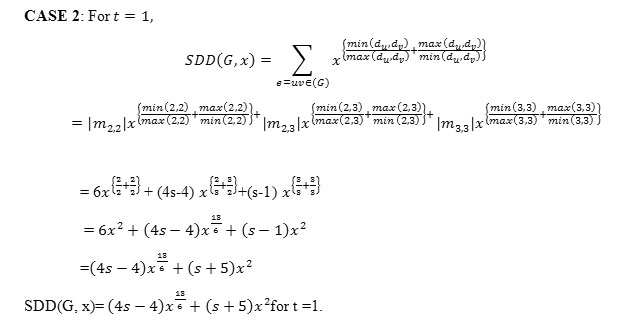
Conclusion

In this article we have computed general formula for third Zagreb index, hyper Zagreb polynomial, first Zagreb polynomial, second Zagreb polynomial third Zagreb polynomial, forgotten index, forgotten polynomial, symmetric division index and symmetric division polynomial of graphene.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this article.

Authors Contributions

All the authors worked together for the preparation of manuscript and all of us take the full responsibility for the content of the article, however first author typed the article and all of us read and approved the final manuscript.

References

1. Jagadeesh R. M. R. Rajesh kanna and Indumathi R. Some results on topological indices of Graphene, Nanomaterials and Nanotechnology, 6, (2016) 1-6.
2. G.Shridhara, M.R Rajesh kanna  and  RS Indumathi. Computation of topological indices of Graphene, Journal of Nanomaterials, Volume (2015) 8 pages.
3. Ali Astanesh-Asl and G.H Fath-Tabar, Computing First and Third Zagreb polynomials of  certain product of graphs, Iranian Jounal of Mathematical Chemistry, 2-2 (2011) 73-78.
4. G.H Shirdel, H.Rezapour and Amsayadi. Hyper Zagreb index of graph operations, Iranian Journal of Mathematical Chemistry, 4(2) (2013) 213-230.
5. B.Furtula and Gutman.I, A forgotten topological index, Journal of Mathematical Chemistry,  53 (2015) 213-220.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.