ISSN : 0970 - 020X, ONLINE ISSN : 2231-5039
     FacebookTwitterLinkedinMendeley

Vibrational Spectra of C2Cl4 Using Lie Algebraic Technique

Volume 35, Number 1

J. Vijayasekhar1, S. Uma Devi2 and T. Sreenivas*3

1Department of Mathematics, GITAM University, Hyderabad, India.

2Department of Engineering Mathematics, Andhra University, India.

3Department of Mathematics, ANITS, Visakhapatnam, India.

Corresponding Autho E-mail: sreenivas.teppala@gmail.com

DOI : http://dx.doi.org/10.13005/ojc/350165

Article Publishing History
Article Received on : 09-01-2019
Article Accepted on : 07-02-2019
Article Published : 26 Feb 2019
Article Metrics
ABSTRACT:

In this paper, we have calculated the vibrational frequencies of medium-size molecule (5-100 atoms), Tetrachloroethylene (C2Cl4) in fundamental mode by one dimensional unitary Lie algebraic technique. In this method, bonds C-Cl and C-C of the Tetrachloroethylene are replaced with a unitary Lie algebras and Hamiltonian expressed in terms of Casimir and Majorana invariant operators and parameters. This Hamiltonian operator describes stretching vibrations of molecule. The determined vibrational frequencies by this theoretical method are compared with experimental results. The obtained results are consistent with experimental results.

KEYWORDS:

Lie Algebraic Technique; Tetrachloroethylene; Vibrational Spectra

Download this article as: 

Copy the following to cite this article:

Vijayasekhar J, Devi S. U, Sreenivas T. Vibrational Spectra of C2Cl4 Using Lie Algebraic Technique. Orient J Chem 2019;35(1).

Copy the following to cite this URL:

Vijayasekhar J, Devi S. U, Sreenivas T. Vibrational Spectra of C2Cl4 Using Lie Algebraic Technique. Orient J Chem 2019;35(1). Available from: https://bit.ly/2H44N0K

Introduction

Spectroscopy today, becomes the most accurate source of information of the spectral structure and energy calculation of molecules. There is considerable present research interest in the analysis of vibrational frequencies of molecules. The emergence of new experimental methods to detect higher vibrational excitations in polyatomic molecules require theoretical methods for their interpretation. In 1991, Iachello and Oss introduced a theoretical method, Lie algebraic method as a computational tool for the analysis and interpretation of experimental and ro-vibrational spectra of molecules. This method is based on the mathematical theory of unitary Lie algebras.1,2

Lie Algebraic Method

The Hamiltonian operator associated with Lie algebraic method3 for n interacting bonds of molecule is

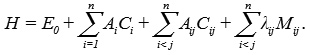
Equation 1

Where, Ci and Cij are invariant operators of the uncoupled and coupled bonds respectively and are given by

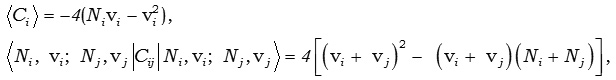
Equation 2

and the Majorana operator Mij is used to describe local mode interactions in pairs and contains both diagonal and non-diagonal matrix elements given by

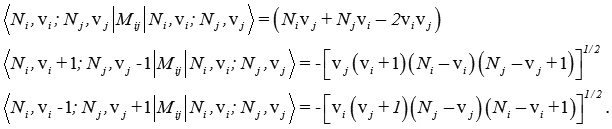
Equation 3

Where, Vi, Vj are vibrational quantum numbers of bonds i and j respectively. The Vibron number Ni is calculated by

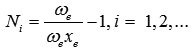
Equation 4

(ωe and ωe xe are the spectroscopic constants6).

We consider a numerical fitting procedure to adjust the parameters and over an experimental results of vibrational energy levels.4,5 The starting guess for the parameter will be obtained by using the energy equation for the single-oscillator fundamental mode as

E(v = 1) = – 4 Ai (Ni – 1).

The parameter λij can be calculated from the relation,

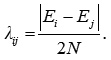
Equation 5

Structure of Tetrachloroethylene

Tetrachloroethylene containing two carbon and four chlorine atoms with one (C-C) and four (C-Cl) bonds. Symmetry species of C2Cl4 are Ag, Au, B1g,  B1u, B2g, B2u, B3u (Point group, D2h).

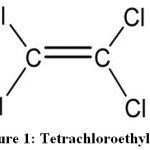Figure 1: Tetrachloroethylene.

Figure 1: Tetrachloroethylene.

Click here to view figure

Results

Table 1: Algebraic parameters.

Stretching parameters
N1= 174 (C-C), N2=132 (C-Cl)
A1 = 9.52, A2 = 8.27 (cm-1)
A12 = 2.321, A13=–1.35 (cm-1)
λ12 = 2.321, λ23=–1.35 (cm-1)

Table 2: Experimental and calculated vibrational frequencies (in cm-1) of C2Cl4.

Symmetry Species Mode Experimental7,8 Calculated
Ag C-C Stretch 1571 1571.38
Ag C-Cl2 Symmetric Stretch 447 446.82
B1g C-Cl2 Asymmetric Stretch 1000 1000.32
B2u C-Cl2 Asymmetric Stretch 908 997.62
B3u C-Cl2 Symmetric Stretch 777 776.61

Conclusion

In this paper we have calculated the vibrational spectra of C2Cl4 in fundamental mode by Lie algebraic method and also compared with available experimental results. These calculations shows that this technique is a reliable appoarch of other theoretical techniques like Ab initio methods.

Acknowledgements

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

References

  1. Iachello, F.; Levine, R. D. Oxford University Press, Oxford. 1995.
  2. Oss, S. Adv. Chem. Phys.1996, 93, 455-649.
  3. Iachello, F.; Oss S. J. Mol. Spectrosc. 1991, 146, 56-78.
    CrossRef
  4. Karumuri, S. R.; Vijayasekhar, J.; Sreeram, V.; Uma Maheswara Rao, V.; Basaveswara Rao, M. V. J. Mol. Spectrosc. 2011, 269, 119-123.
    CrossRef
  5. Karumuri, S. R.; Girija Sravani, K.; Vijayasekhar, J.; Reddy, L. S. S. Acta Phys. Pol. A. 2012, 122(1), 1111-1114.
  6. K. Nakamoto. Wiley-interscience, New York. 1978.
  7. Shimanouchi, T, Tables of Molecular Vibrational Frequencies Consolidated Volume I, National Bureau of Standards, 1972.
    CrossRef
  8. Karl K. Irikura, J. Phys. Chem. Ref. Data. 2007, 36(2), 389-397.
    CrossRef

Creative Commons License
This work is licensed under a Creative Commons Attribution 4.0 International License.