Theoretical Investigation of Application of Combining Pristine C₆₀ and Doped C₆₀ with Silicon and Germanium Atoms for Solar Cells ; A DFT Study

Introduction

Solar energy is an important energy sources nowadays. The sun gives to the earth surface in so much energy in a day that it could be enough to cover the daily need of the population of our planet. Photovoltaic devices and solar cells are the most simple and efficient conversion of the solar energy to electricity.¹

Organic solar cell research has developed during the past 30 years, but in the last decade it has attracted scientific and economic interest because of a rapid increased need for electrical power. Scientists have achieved new materials, improved materials engineering, and more advanced device structures.² The search for new materials has been extended into the field of organic polymers , inorganic  and semi conducting molecules that their optical, electrochemical and electrical properties can offer wide conversion of the solar energy to electricity. Organic semiconductors are used to be described as conjugated oligomers or polymers which are able to transporting charge carriers. Holes and electrons in p-orbitals are the typical charge carriers in organic semiconductors. Charge transport depends on the movement of the charge carriers to from one molecule to another and depends on the energy gap between highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) levels.³

The basic operation of solar cells is summarized in four steps which are illustrated in figure  (1): 1- photon absorption leading to exciton generation; 2- exciton diffusion to a donor/ acceptor heterojunction; 3- exciton dissociation at a heterojunction to form geminate pairs; 4- carrier transport and carrier extraction at the electrodes.⁴

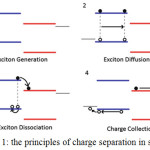Figure 1: The principles of charge separation in solar cell.4 Click here to view figure

Organic solar cells are basically consist of a p-type semiconductor as donor and a n-type semiconductor as acceptor. At the donor–acceptor interface, charges are separated after photo-induced charge transfer from the electron donor to the electron acceptor. Figure (2) shows a schematic frontier orbital energy levels and the basic fundamental steps which happens in a typically Organic solar cell.³

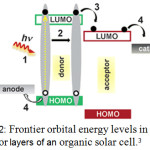Figure 2: Frontier orbital energy levels in donor-acceptor layers of an organic solar cell.3 Click here to view figure

Bulk heterojunction (BHJ) structure is the most successful method for a solar cell can be a blend of donor and acceptor materials with a bicontinual phase separation.⁵ Many fullerene-based molecules can be used in organic photovoltaic devices for the reason that fullerene is good p-electron acceptor which can be connected with other organic molecules.⁶ This observation lead us to the C₆₀ molecule and how there can be increase in photo-conductivity properties upon addition of C₆₀ to other conjugated polymers.

The buckminster fullerene C₆₀ and its derivatives are strong electron acceptors.²

In this paper, First, HOMO and LUMO levels a fullerene C₆₀ and its doped with one, two and three Silicon and Germanium atoms are calculated and compared. Then, with equations and approximate calculations, suitable donors and acceptors for organic solar cell will be selected. In the end, The theoretical UV-VIS absorptions of these donors/acceptors are used to confirm of calculated results.

Computional method

DFT functional methods PBE and HCTH with  6–31+G(d) basis set are used to calculate HOMO and LUMO levels a fullerene C60.⁷ and its doped complexes configurations which contain 1-3 doped Silicon atoms and 1-3 doped Germanium, respectively. Silicon and Germanium are semiconductors chosen from forth group of the periodic table of elements. All calculations were performed by package GAUSSIAN 03. Vibration frequencies were also calculated at the same level to confirm that all the stationary points correspond to true minima on the potential energy surface. Td=NSTATES=10 is used for determination  theoretical UV-VIS absorptions  of donors/acceptors as solar cells.

Two factors are important to select among the calculated HOMO and LUMO levels for the solar cell. First, the band gap of approximately 0.3–0.4 eV between the LUMO of the donor and the LUMO of the acceptor is necessary to ensure efficient exciton dissociation at the D/A interface.³ Second, for commonly large band gap of organic materials and small absorption range, a LUMO–HOMO difference (E gap) of 1.1 eV of the donor can show good results.⁴

Results and Discussion

Calculation HOMO and LUMO levels

In the first step of this work, HOMO and LUMO levels of C₆₀ and its doped derivatives such as C₅₉Si, C₅₈Si₂, C₅₇Si₃, C₅₉Ge, C₅₈Ge₂, C₅₇Ge₃ and C₅₈GSi is calculated with DFT functional methods PBE and HCTH. The results are shown in tables (1), (2), (3) and (4).

The calculated E gaps in table (1) Shows a E gap of 1.65( PBE method) and 1.68 (HCTH method) for C₆₀. Titus A. Beu, Jun Onoe, and Akira Hida have calculated The E gap of C₆₀ with these two method and reach the same results.⁷ LUMO–HOMO difference shows that C₆₀ is not a suitable for a donor compound, so as it was said before. C₆₀ is considered as an acceptor. Tables (2) and (3) show us that doping C₆₀ with semiconductor atoms such as Silicon and Germanium can descries their band gaps which are around 1.1 eV and can be considered as assumed donors in the solar cell.

The second factor, as it was said, is the difference between the LUMO of the donor and the LUMO of the acceptor which must be 0.3–0.4 eV. The calculated LUMOs with PBE and  HCTH methods in tables1, 2 and 3 show us that the best candidates for donor compounds are C₅₉Si, C₅₉Ge. The differences between of LUMOs for C₅₈Ge₂ and C60, C₅₈GeSi  with C₆₀ both with PBE and HCTH methods are near 0.3 eV, so they can be considered as candidates for donor compounds.

Table 1: HOMO and LUMO energy levels and Egap of C₆₀.

Compound	Method	HOMO(eV)	LUMO(eV)	E gap
C60	PBE	-5.86	-4.21	1.65
C60	HCTH	-5.97	-4.29	1.68

Table 2: HOMO and LUMO energy levels and Egap of  doped C₆₀ with Silicon.

Compound	Method	HOMO(eV)	LUMO(eV)	E gap
C59Si	PBE	-5.69	-4.51	1.18
C59Si	HCTH	-5.78	-4.59	1.19
C58Si2	PBE	-5.52	-4.45	1.07
C58Si2	HCTH	-5.61	-4.52	1.09
C57Si3	PBE	-5.43	-4.26	1.17
C57Si3	HCTH	-5.43	-4.26	1.17

Table 3: HOMO and LUMO energy levels and Egap of  doped C₆₀ with Germanium.

Compound	Method	HOMO(eV)	LUMO(eV)	E gap
C59Ge	PBE	-5.72	-4.59	1.13
C59Ge	HCTH	-5.80	-4.67	1.13
C58Ge2	PBE	-5.47	-4.50	0.97
C58Ge2	HCTH	-5.55	-4.57	0.98
C57Ge3	PBE	-5.32	-4.25	1.07
C57Ge3	HCTH	-5.39	-4.31	1.08

Table 4: HOMO and LUMO energy levels and Egap of  doped C₆₀ with  Silicon and Germanium.

Compound	Method	HOMO(eV)	LUMO(eV)	E gap
C58GeSi	PBE	-5.53	-4.50	1.03
C58GeSi	HCTH	-5.61	-4.57	1.04

Theoretical Determination of Performance of Donor-Acceptor

Calculation of Voc

V_OC (open-circuit voltage) represents the maximum voltage measured in a solar cell, which depends mainly on the energetic levels of frontier orbitals of the used organic material. It means the energy difference of the HOMO level of the donor (D) and the LUMO level of the acceptor (A).³ The parameter Voc can be calculated by the empirical equation.

Voc =(1/e)(|E_H(D)|−|E_L(A)|)−0.3 V            (1)

e, E_H(D) and E_L(A) are the elementary charge, the HOMO energy of donor and the LUMO energy of acceptor, and 0.3 V is an empirical factor for efficient charge separation.⁸ Ac The computed values of Voc for the chosen donors – acceptors calculated by equation (1) are listed in table 5.

Determination  of Jsc

J_SC (short-circuit current density) represents the maximum current that could be obtained in a solar cell. Calculation of Jsc is a great importance for the further improvement of a organic solar cell. In this research for determining Jsc, the incident light intensity dependence of Jsc is used. A power law dependence of Jsc upon light intensity I is reported which is represented in equation (2).

where α ranges typically from 0.85 to 1 for polymer/ fullerene based solar cells.⁹ OSCs are typically characterized under 1000 W/m² light of AM 1.5 solar spectrum and temperature 25°C.³ According to equation (2), Jsc varies between 354.81 W/m² and 1000 W/m² . In this work, the average for Jsc is considered which is 677.4 W/m².

Determination of (FF) and Power Output (P_out)

The fill factor (FF) describes the quality of the solar cell and is determined by the photogenerated charge carriers and the fraction thereof that reaches the electrodes.⁸ For the FF calculation under ideal conditions, an approximation can be expressed as:

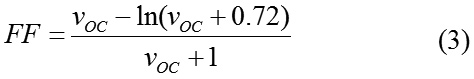
where V_OC is the dimensionless voltage Voc and can be calculated by equation (4)

Here k, T and q are the Boltzmann constant, the temperature (300 K) and the elementary charge, respectively.¹⁰ The last step in theoretical determination of efficiency of the donor-acceptors candidates for organic solar cells is calculating power output for each donor- acceptor which is calculated by equation (5).³

P_out = V_OC × J_SC × FF                                   (5)

If the standard light intensity (1000 W/m² light of AM 1.5 solar spectrum) considered as the input power density ( P_in) , the power conversion efficiency (PCE) of the solar cell and can be calculated  as equation (6).⁴

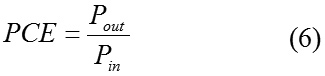
The calculated V_OC fill factor, power output and power conversion efficiency of solar cells consist of C₆₀ as acceptor and C₆₀ doped derivatives as donors are listed in table 5.

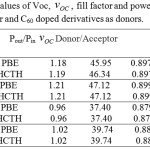Table 5: The computed values of Voc, VOC fill factor and power output for C60 as acceptor and C60 doped derivatives as donors. Click here to view table

Study of theoretical UV- VIS spetrums

In the next step of this research, with using Td=NSTATES=10, UV- VIS spectrums of C₆₀, C₅₉Si, C₅₉Ge, C₅₉Si/C₆₀, C₅₉Ge/C₆₀, C₅₈Ge₂/C₆₀ and C₅₈GeSi/C₆₀ are calculated. These spectrums shows parameters such as  absorption wavelengths , oscillator strength  and  coefficient absorption of  these derivatives and donors/acceptors which can be compared.

Oscillator strength which represents the average number of electrons per atom that can be excited by the incident radiation. It is an important factor for providing the relative strength of electron transition and can be related with the molar absorption coefficient (ε) as a function of frequency (equation 7). Oscillator strength ranges between 0 and 1.¹¹

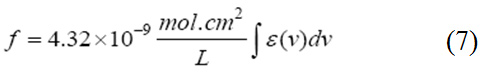
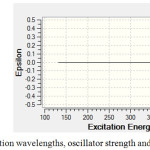Figure 3: Calculated absorption wavelengths, oscillator strength and coefficient absorption of C60. Click here to view figure

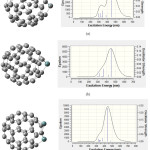Figure 4: Calculated absorption wavelengths, oscillator strength and coefficient absorption of (a) C59Si (b) C59Ge, (c) C58Ge2. Click here to view figure

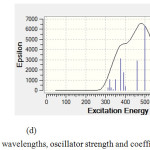Figure 5: Calculated absorption wavelengths, oscillator strength and coefficient absorption of (d) C59SiGe. Click here to view figure

Although we see sunlight (or white light) as uniform or homogeneous in color, it is actually composed of a broad range of radiation wavelengths in the ultraviolet (UV), visible and infrared (IR) portions of the spectrum .Visible wavelengths cover a range from approximately 400 to 780 nm, ultraviolet 1- 400 nm and near infrared 780 nm- 2.5 μm.

Figure (3) shows C₆₀ has no absorption in UV-VIS spectrum while in figures (4) and (5) there is one major absorption peak for C₅₉Si, C₅₉Ge, C₅₈Ge₂ and C₅₈SiGe in wavelength range 300-600 nm. C₅₉Si and C₅₈SiGe have a minor absorption peak in range 300-400 nm which can be related to the doped silicon atom. Maximum coefficient absorption for C₅₉Si, C₅₉Ge , C₅₈Ge₂ and C₅₈SGe approximately are 4500 epsilon in 452.3 nm, 5500 epsilon in 452.28 nm , 9900 epsilon in 445.85 nm and 6500 epsilon in 500 nm, respectively. The results indicates that these four doped derivatives not only have good absorptions in visible spectrum but also with doping Germanium atom instead Silicon atom Maximum absorption wavelength shifts to higher wavelength with higher coefficient absorption.

Figures (4) and (5) also show excitation energies and their oscillator Strength in UV/ VIS spectrum of each absorption peak for the four doped derivatives. Some of the excitation energies which have stronger oscillator Strength are listed in table (6). For C₅₉Si, its spectrum shows the strongest excitation energy happened in 425.3 nm with oscillator Strength 0.1059 and there are minor excitation energies with weak oscillator Strength which mostly happened in ultraviolet range. In C₅₉Ge spectrum, the strongest excitation energy has shifted to 452.28 nm with oscillator Strength 0.13 while the strongest excitation energy for C₅₈Ge₂ happened in 445.85 nm with 0.2319. we can conclude that stronger maximum oscillator strength in visible range is the result of doping one or two Germanium atoms instead silicon atom in C₆₀ . Just like C₅₉Si, the two derivatives C₅₉Ge and C₅₈Ge₂ have excitation energies with weaker oscillator strength in ultraviolet range.

As for C₅₉GeSi, it seems doping one atom Germanium along with one atom Silicon made the excitation energies in 300-450 nm with stronger oscillator strength than the three discussed  derivatives but  it seems the Silicon atom has made decrease in  oscillator strength of maximum excitation energy which is 0.1154 in 500.22 nm.

The main purpose of this work is comparing the absorption peaks and oscillator Strength of these compounds when they are chosen as donors while C₆₀ is considered as acceptor. To obtain their UV-VIS spectrum, the donor derivatives are considered in a constant distant 1.8 A away from C₆₀. Table (6) shows us the comparison of absorption wavelengths and oscillator Strength of the chosen donor-acceptor compounds.

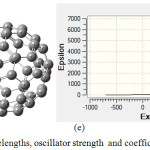Figure 6: Calculated absorption wavelengths, oscillator strength and coefficient absorption of (e) C59Si/C60. Click here to view figure

Figure (6e) belongs to C₅₉Si/C60 which its spectrum shows two absorption peak, one is about 300-600 nm with maximum coefficient absorption 5000 epsilon in 400 nm which can be related to absorption of C₅₉Si and a second one which is about 800-2500nm with maximum coefficient absorption 6500 epsilon in 1265.21 nm. This absorption can be considered as electron transfer from C₅₉Si to C₆₀ which happened in infrared range. Comparing excitation energies of C₅₉Si with C₅₉Si/C₆₀ which are listed in table (6) show us that coupling C₅₉Si with C₆₀ as donor-acceptor not only has made the excitation energies in 300-600 nm with stronger oscillator strength with higher wavelengths but also maximum coefficient absorption has increased from 4500 epsilon in visible range ( for C₅₉Si)  to 6500 epsilon in infrared range (for C₅₉Si/C₆₀).

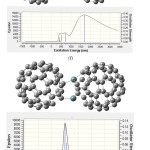Figure 7: Calculated absorption wavelengths, oscillator strength  and coefficient absorption of (f) C59Ge/C60 and  (g) C58Ge2/C60. Click here to view figure

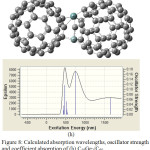Figure 8: Calculated absorption wavelengths, oscillator strength and coefficient absorption of (h) C58Ge2/C60. Click here to view figure

In the next step, C60 is doped once with one Germanium as C₅₉Ge/C₆₀ and also with two Germanium atoms as C₅₈Ge₂/C₆₀. The UV/VIS spectrum of C₅₉Ge/C₆₀ (figure 7f) show two absorption peak with maximum coefficient absorptions 5000 epsilon in 720.72 nm and 15000 epsilon in 1687.24 nm, respectively. As for C₅₈Ge₂/C₆₀, there is only one absorption peak with maximum coefficient absorptions 9500 epsilon in 500 nm. Also figure (7f) shows a bonding for electron transfer between the doped Germanium atom and one of Carbon atoms in C60 but in figure (7g) one of the two doped Germanium atoms and also one of Carbon atoms of C₆₀ have lost their bonding to create a new ring which happened among two doped Germanium atoms of C₅₈Ge₂ and Carbon atoms of C₆₀. This may explain only one absorption peak in the UV-VIS spectrum of C₅₈Ge₂/C₆₀.

In C₅₉Ge/C₆₀ spectrum, stronger excitation energies has happened with oscillator Strength 0.0616, 0.0951, 0.1136 and 0.3736 in 400.3 nm, 524.54 nm, 720.72 nm and 1687.24 nm, respectively while in C₅₈Ge₂/C₆₀ spectrum, stronger excitation energies with oscillator Strength 0.01272 and  0.0643 are in 506.86 nm and 570 nm which has occurred in visible range. Some of excitation energies and their oscillator Strength of these two donors-acceptors are listed in table (6). These results shows C₅₉Ge/C₆₀ has a good absorption in both visible and infrared range because of doping one Germanium atom but by doping two Germanium atoms not only the structure of donor and acceptor.

Table 6: Absorption wavelengths, oscillator strength of doped C₆₀ derivatives and donors-acceptors compounds.

Compound	Absorption Wavelengths (nm)	Oscillator Strength
C59Si	297.96	0.012
	316.01	0.0129
	342.95	0.0229
	388.21	0.007
	452.3	0.1059
C59Ge	316.57	0.0161
	366.18	0.0368
	418.44	0.009
	452.28	0.13
C58Ge2	328.27	0.0174
	375.42	0.0245
	445.85	0.2319
C58GeSi	322.22	0.018
	351.49	0.0184
	376.62	0.0531
	393.15	0.0298
	460.96	0.0501
	500.22	0.1154
C59Si/C60	342.75	0.0195
	375.68	0.0283
	393.8	0.0638
	423.16	0.0246
	445.91	0.015
	539.61	0.0124
	1265.21	0.1623
C59Ge/C60	400.3	0.0616
	524.54	0.0951
	720.72	0.1136
	1687.24	0.3736
C58Ge2/C60	433.23	0.0182
	456.57	0.0283
	506.86	0.1272
	570.49	0.0643
	791.74	0.0161
	1185.85	0.0106
C58SiGe/C60	432.6	0.0164
	445.1	0.0344
	464.57	0.1161
	518.31	0.0511
	530.42	0.0118
	752.36	0.187
	1642.2	0.0672

Compounds may change but also there will be a decrease in maximum absorption and oscillator Strength UV-VIS spectrum of C₅₈SiGe/C₆₀ (figure 8) shows three absorption peak, the first one is about 300-600 nm with maximum coefficient absorption 8500 epsilon that can be related to absorption of C₅₉Si. In this case excitation energies which has happened in 300-600 nm have stronger oscillator strength than C₅₉Si such as 0.1161 in 464.57 nm (table 6). The increase of excitation energies can be result of doping Germanium atom along side Silicon atom. The second and third peak are about 600-1000nm and 1200- 2000nm with maximum coefficient absorptions 7500 epsilon and 3000 epsilon, respectively. Figure (8) shows, Germanium atom has two bonds with Carbon atoms in C₆₀ while Silicon atom has one bond. As Germanium shows more tendency in being donor than Silicon Atom, we can assume that the second peak is related to electron transfer from Germanium atom to C₆₀ which happened with oscillator strength 0.187 in 752.36nm. Figure (8) also show us a ring between donor and acceptor and it consist of Germanium and Silicon doped atoms and Carbon atom of C₆₀. The electron movements in this ring can result the third absorption peak with oscillator strength 0.0672 in 1642.2nm ( table 6).

Conclusion

C₆₀ is a good acceptor and has no absorption in sunlight range. The theoretical research indicates that by doping  C₆₀ with Silicon and Germanium atom, the derivatives will have donor property and can have absorptions in ultraviolet and visible range of sunlight. Furthermore, the results of equations and theoretical UV- VIS spectrums indicates that, when these doped derivatives are used as donor with C₆₀ as their acceptor for basic of a solar cell, the resulted solar cells will have absorption in visible and infrared range of sunlight.

Acknowledgments

The author wishes to thank to the department of chemistry, College of Basic Sciences of Islamic Azad University, Yadegar-e-Imam Khomeini (RAH) Branch for supporting this study specially with computers to perform this research.

References

1. Liang, Y.; Xu, Z.; Xia, J.; Tsai, S. T. ; Wu, Y.; Li, G.; Ray, C.; Yu, L. Adv. Mater. 2010, 22, 135-138.
   CrossRef
2. Hoppea, H.; Sariciftci, N. S. Organic. J. Mater. Res. 2004, 19, 1924-1945.
   CrossRef
3. Mishra, A.; Bauerle, P. Angew. Chem. Int. Ed. 2012, 51, 2020-2067.
   CrossRef
4. Fung, D. D. S.; Choy, W. C. H. Organic. Springer-Verlag . 2013, 1, 1-16.
   CrossRef
5. Azazi, A.; Mabrouk, A.; Chemek, M.; Kreher, D.; Alimi, K. Synthetic Metals. 2014,198, 314-322.
   CrossRef
6. Shalabi, A.S.; Abdel Aal, S.; Assem, M.M.; Soliman, K.A. Organic Electronics. 2012,13. 2063-2074.
   CrossRef
7. Beu, T. A.; Onoe, J.; Hida, A. Physical Review B . 2005, 79,155416(1)-155416(5).
8. Liu, X.; Huang, C.; Shen, W.; He, R.; Li, M. J. Mol.Model. 2016, 22(15), 1-11.
   CrossRef
9. Koster, L. J. A.; Mihailetchi, V. D.; Xie, H.; Blom, P. W. M. Applied Physics Letters. 2005, 87, 203502(1)-203502(3).
   CrossRef
10. Gupta, D; Mukhopadhyay, S; Narayan, K. Sol Energy Mater Sol Cells. 2010, 94(8), 1309-1313.
    CrossRef
11. Abraha, A.; Gholap, A.V.; Belay, A. International Journal of Biophysics. 2016, 6(2), 16-20.
12. Kako, M.; Nagase, S.; Akasaka, T. Molecules. 2017, 22, 1179(1)-1179(17).
    CrossRef
13. Labrunie, A.; Gorenflot, J.; Babics, M.; Alévêque, O.; Dabos-Seignon, S.; Balawi, A.H.; Kan, Z.; Wohlfahrt, M.; Levillain, E.; Hudhomme, P.; Beaujuge, P.M.; Laquai, F.; Cabanetos, C.; Blanchard, P.Chemistry of Materials. 2018,30(10), 3474-3485.
    CrossRef
14. Zheng, Z.; Tummala, N. R.; Fu, Y. T.; Coropceanu, V.; Bredas, J.L. ACS Appl. Mater. Interfaces, 2017, 9 (21), 18095-18102.
    CrossRef
15. Joseph, S.; Ravva, M.K.; Bredas, J.L. J. Phys. Chem. Lett., 2017, 8 (20), 5171-5176.
    CrossRef

---

This work is licensed under a Creative Commons Attribution 4.0 International License.