Resonance Raman Spectra of Erythrocytes: Vibron Model

Introduction

Molecular spectroscopy is a key tool for the explanation of molecular structure. The study of fundamental and higher overtones of molecule helps in better understanding of the molecular structure, which might have a great importance in medical science. This spectra is useful to analyse biological molecules for identifying diseases in near the beginning stage and also useful to compare in vivo experimental results. The frame of new experimental methods to identify higher vibrational excitations in polyatomic molecules requires theoretical models (example, Vibron model) for their interpretation. Vibrational spectra of molecules are analysed with the help of two well- known approaches Dunham expansion and Potential approach. The most serious drawback of these approaches is that large number of parameters required for polyatomic molecules. To overcome this difficulty, we consider the Vibron model.^1,2 In 1991, Iachello presented Vibron model in the study of spectra of molecules.^3,4,5,6

Vibron model

The Vibron model (Hamiltonian) for polyatomic molecule is

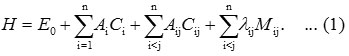
Here (A_i, A_ij, λ_ij) are parameters (algebraic) and  (C_ij,C_ij,M_ij) are algebraic operators, which are differ from molecule to molecule. Algebraic operators, C_i and C_ij are invariant operators associated with uncoupled and coupled bonds with diagonal with matrix elements. The Majorana operator, M_ij associated with coupling schemes. Algebraic parameters can be determined by spectroscopic data. Algebraic operators can be determined by

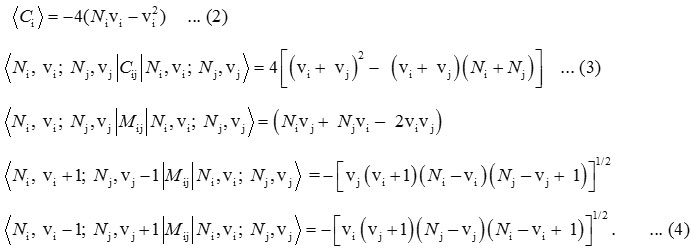
In above equations, N_i, v_i (i=1,2,…) represents Vibron and vibrational quantum numbers respectively.

The vibron number N_i for stretching bonds of molecule will be calculated by

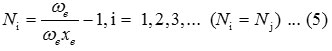
Here ω and ω_e x_e are the spectroscopic constants. The initial guess value for the parameter A_i is obtained by using the energy equation, which is known as,

The first guess for A_i can be taken as zero. The parameter λ_ij obtained from the relation,

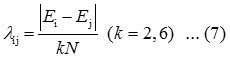
Results

From the group theory point of view, the molecule of oxygenated and deoxygenated erythrocytes is a square planar structure with the D_4t  symmetry point group.⁸ We considered a experimental data from high-quality Raman speectra of red blood cells in both the oxygenated and the deoxygenated states for cell at 782 nm.⁷

Table 1: Vibrational spectra of erythrocytes.

Symmetry Species3	Vibrational mode	Vibrational frequencies (cm-1)
		Calculated	Experimental7
oxynated erythrocytes
B1g	(Cm-H)	1305.2346	1306
Eu	(Cm-H)	1250.0429	1248
deoxynated erythrocytes
B1g	(Cm-H)	1303.0086	1305
Eu	(Cm-H)	1244.9821	1248

 

Table 2: Algebraic parameters.

Algebraic parameters	oxynated	deoxynated
A	-9.3485	-10.5453
λ	0.3581	0.1277
N	44	44

 

Values of algebraic parameters in cm^-1, but N is dimensionless.

Conclusion

In this paper we have calculated the vibrational frequencies of oxynated and deoxynated erythrocytes for the vibrational mode (C_m-H) by Vibron model and also compared with experimental data. These calculations shows that this model is an alternative appoarch of other theoretical models like Ab initio methods.

References

1. Iachello, F.; Levine, R. D. Oxford University Press, Oxford.1995.
2. Oss, S. Adv. Chem. Phys.1996, 93, 455-649.
3. Karumuri, S. R.; Vijayasekhar, J.; Sreeram, V.; Uma Maheswara Rao, V.; Basaveswara Rao, M. V. J. Mol. Spectrosc. 2011, 269, 119-123.
   CrossRef
4. Karumuri, S. R.; Srinivas, G.; Vijayasekhar, J.; Rao, V. U. M.; Srinivas, Y.; Sunil Babu, K.; Kumar, V. S. S.; Hanumaiah, A. Chin. Phy. B. 2013, 22(9), 090304(1-8).
5. Vijayasekhar, J.; Karumuri, S. R.; Rao, V. U. M. Natural Science. 2012, 4(10), 792-796.
   CrossRef
6. Karumuri, S. R.; Rao, V. U. M.; Vijayasekhar, J. Proc. Materials Science, 2015, 10, 737-747.
7. Bayden R. Wood; Peter Caspers; Gerwin J. Pupples. Anal. Bioanal. Chem. 2007, 387, 1691-1703.
   CrossRef
8. Karumuri, S. R.;  Sravani, K.G. Mol. Phys. 2016, 114(5), 643-649.
   CrossRef

---

This work is licensed under a Creative Commons Attribution 4.0 International License.