Volumetric and Ultrasonic Velocity Studies of Urea and Thiourea in Aqueous Solution

Introduction

The physico-chemical interaction between various essential molecules in a living organism and cosolutes are very important. Urea is highly active compound  in a variety of biological functions in our body and has been referred as protein denaturing agent. Urea provides a significant role in the metabolism of compounds having nitrogen by animals and the highest amount of substance contain nitrogen in the urine of mammals. Body use it in various functions; the most important is nitrogen excretion. Further, urea is an essential basic material for the chemical industry. Thiourea is structurally similar to urea except that the oxygen atom in urea is replaced by a sulfur atom, although the properties of urea & thiourea differ considerably. Thiourea is also a valuable reagent in organic synthesis processes and employed as a source of sulfide. Substituted thioureas are beneficial catalysts for many organic synthesis reactions. Other industrial applications of thiourea such as production of flame retardant resins, vulcanization accelerators, auxiliary agent in diazo paper & light-sensitive photocopy paper and used to tone silver-gelatin photographic prints are also useful applications.

The volumetric and ultrasonic sound velocity data deliver valuable information about the interactions such as solute-solute, solute-solvent etc. Maximum researcher reported that^1,2 urea behave as structure breaker in water. Some researcher reported that urea perform as a structure maker³ in water.  On the other hand, it has been shown that by thermo-chemical & NMR studies of urea has no basically net effect on the structure of water.⁴ So, the interaction of urea with water is not yet clearly discussed. For clear observations about the urea effect on water, we study the various parameters of molecular interaction in aqueous urea solutions through volumetric and ultrasonic measurements and also studied the comparison between urea and thiourea. The ultrasonic sound velocity and density measurements^5,6 and their derived parameter such as, apparent molar volume, limiting apparent molar volume, apparent molar expansibility, adiabatic compressibility, apparent molar adiabatic compressibility and hydration number^7,8 find wide applications in characterizing the physico-chemical behavior of solution mixture.

Experimental Details

Materials

Urea (Purity declared by supplier, mass fraction >0.995 % with molar mass 0.06006 kg.mol⁻¹) and thiourea (Purity confirmed by supplier, mass fraction >0.995 % with molar mass 0.07612 kg.mol⁻¹) was collected from Loba Chemie Pvt. Ltd, India.

Measurement of Density and Ultasonic Sound Velocity

The solutions were prepared by using freshly redistilled and degassed water (specific conductance < 10⁻⁶ S cm⁻¹). The solutions were prepared (in molality) by weighing on a balance (Mettler Toledo, B204-S, Switzerland) having an accuracy of ± 0.0001g. The densities (ρ) and ultrasonic sound velocity (u) of the solutions were instantly and automatically measured using a density and ultrasonic sound velocity analyzer (DSA 5000, Anton Paar, Austria). A density check or an adjustment of air/water was done at 20°C by using triply distilled, degassed water and dry air at atmospheric pressure. Before measurements, the analyzer was calibrated with redistilled & degassed water in the selection experimental temperature range. Both the density and ultrasonic sound velocity are very sensitive to temperature, thus it was organized to ± 1·10⁻³ K by a built-in Peltier device. The sensitivity of the instrument relates to a precision in density and ultrasonic sound velocity measurements of 1·10⁻³ kg m⁻³ and 1·10⁻² m s⁻¹.⁹

Result and Discussions

Apparent molar volume & apparent molar adiabatic compressibility

The apparent molar volume (ϕ_v) & apparent molar adiabatic compressibility (ϕ_k) are very valuable parameters in the understanding of interactions between solute-solvent and solute-solute. The density and ultrasonic sound velocity data are used to calculate ϕ_v, β_s and ϕ_k  by using the relations² (1), (2) & (3).

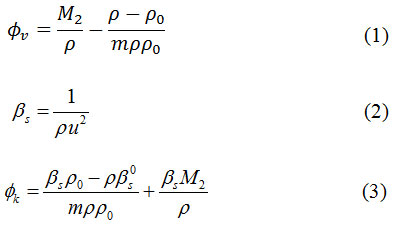
Where m/(mol kg⁻¹) is the molality of urea/thiourea in aqueous solutions,

ρ/(kg m⁻³) is the density of urea/thiourea solution,

ρ⁰/(kg m⁻³) is the density of solvent and

M₂/(kg mol⁻¹) is the molar mass of urea/thiourea.

The experimental density (ρ) and ultrasonic sound velocity (u) of aqueous solution of urea & thiourea are represented in Table 1. & Table 2. as a function of  molality urea & thiourea and temperature. The ϕ_v values are represented in Table 1. The ϕ_v values of urea and thiourea in water at different concentration are also graphically presented in Figure 1(a) and Figure 1(b) respectively. From the data, it is clearly observed that ϕ_v values of urea & thiourea increase with both the increase in concentration and increase in temperature. The usual explanation is that the interactions of solute species follows through the destructive overlap of their hydration spheres.¹⁰ Urea (H₂N–CO–NH₂) and thiourea (H₂N–CS–NH₂) molecules contain –NH₂, –CO  and –CS groups which are hydrophilic groups. So, interaction between solute and water molecules complete through hydrophilic hydration. The interaction of two hydrophilic hydration co-spheres releases some water molecules from the hydration sphere to the bulk results of an increase in volume with an increase in the concentration of urea & thiourea. As the temperature is increased several water molecules from the hydration co-sphere relaxes from the cosphere to the bulk due to thermal agitation thereby increasing the ϕ_v. Thiourea contain a less hydrophilicity sulfer group, in presence of these group (–CS….H₂O) hydrogen bond in thiourea is weak and less compact hydration than (–CO….H₂O) hydrogen bond in urea molecule. For this reason ϕ_v values are greater in thiourea.

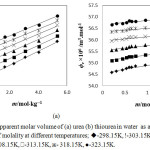Figure 1: Apparent molar volume of (a) urea (b) thiourea in water  as a function of molality at different temperatures; ◊-298.15K, i-303.15K, Δ-308.15K, -313.15K, ж- 318.15K, ●-323.15K. Click here to View figure

 

The calculated ϕ_k values of urea and thiourea in water at different temperatures are represented in Table 2. The ϕ_k values of urea and thiourea in water are graphically presented in Figure 2(c) and Figure 2(d) respectively. The ϕ_k values are gradually changes and become negative when the temperature and concentration of urea and thiourea are low. The solute-solute interactions involve the interactions between hydrophilic-hydrophilic hydration spheres. These interactions between the co-spheres of hydrophilic groups result the relaxation of water molecules from hydrophilic zone to bulk. The water molecule relaxation from hydrophilic zone to bulk results the positive change in f_k. The hydrophilic effect always produce overall positive effect on f_k causing an increase in apparent molar adiabatic compressibility with the concentration of solutes. More water molecules relaxes from hydrophilic zone to bulk in thiourea solutions due to the week (–CS….H₂O) hydrogen bond, which makes the more positive change in f_k values for thiourea compare with urea solution.

Figure 2: Apparent molar adiabatic compressibility of (c) urea (d) thiourea in water  as a function of molality at different temperatures; u-298.15K, !-303.15K, p-308.15K, -313.15K, ж- 318.15K, ●-323.15K. Click here to View figure

 

Limiting Apparent Molar Volume & limiting Apparent Molar Adiabatic Compressibility

The limiting apparent molar volume (ϕ_v⁰) and limiting apparent molar adiabatic compressibility  (ϕ_k⁰) values were attained by least squares method to the equation (4) and (5).

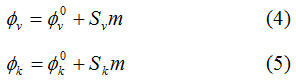
The ϕ_v⁰ and ϕ_k⁰ values of urea and thiourea in water are reported in Table 1. and Table 2. respectively against the concentration of urea & thiourea at various temperatures. It is clearly observed that the values of  ϕ_v⁰ are positive and increase with increase in temperature, which indicates that there exists strong interactions between solute-solvent that are more suitable at higher temperatures. The ϕ_v⁰ increase with increase in temperature may be owing to the following facts: (i) at higher temperature due to the increasing thermal energy of water molecules, the hydrophilic water molecules is relaxed from the interaction regions of –NH₂, –CO and –CS groups of urea, thiourea molecules results of a positive volume change & (ii) the interactions between water and water decreases with increase in temperature giving rise a very small negative change in volume. The linear increasing change of ϕ_v with molality shows that the interactions between urea and water increase with the increase in concentration of urea at the experimental temperatures. Similar nature was stated previously by concentration dependence studies of apparent molar volume of aqueous solutions of  urea by Stokes.¹¹

It was observed that the values of  ϕ_k⁰ are negative at low temperatures & the magnitudes of ϕ_k⁰ values increase with increase in temperature and become positive in magnitude at higher experimental temperatures. The negative values of ϕ_k⁰ specify that the water molecules surrounding urea & thiourea are less compressible than that are present in bulk medium  and increase in magnitude or become positive at elevated temperature, which may be recognized to the melting of rigid hydration structures around the urea and thiourea molecule. The water molecules exist in the monomeric form are more compressible.

Hydration number

The hydration number of amino acid was calculated using equation¹²(6)

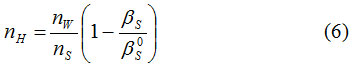
where n_w  is the number of  moles of water

n_s is the number of  moles of solute,

β_s/Pa⁻¹ is the adiabatic compressibility of  aqueous  solution and

β_s⁰/Pa⁻¹ is the adiabatic compressibility of urea and thiourea in aqueous solution.

The hydration number of urea and thiourea calculated by above equation are listed in Table 2. The n_H values of urea and thiourea in water are also graphically represented in Figure 3(e) and Figure 3(f) respectively. From the data, it is observed that n_H values of urea & thiourea decrease with increase in the temperature and with increase in concentration of urea and thiourea.

The decrease in hydration number with the increase in urea and thiourea molality is attributed to the removal of H₂O molecules from the hydration sphere due to the overlap of cospheres of urea and thiourea molecules. As the temperature is increased some H₂O molecules from hydration cosphere relaxes to the bulk due to thermal agitation thereby decreasing the hydration number. n_H of thiourea is more than the urea  due to the bigger sulphur atom which is  less hydrophilic than oxygen atom in urea molecule. Due to the increasing hydrophobicity behavior of thiourea, more hydration number observes for thiourea than urea in solution.

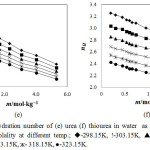Figure 3: Hydration number of (e) urea (f) thiourea in water  as a function of molality at different temp.; ◊-298.15K, !-303.15K, p-308.15K, -313.15K, ж- 318.15K, ●-323.15K. Click here to View figure

 

Table 1: Densities, ρ/kg.m⁻³, apparent molar volume, ϕ_v /(10^-6·m³·mol⁻¹ ) and limiting apparent molar volume,  ϕ_v⁰/(10^-6·m³·mol⁻¹ ) of urea and thiourea in aqueous solutions at 298.15, 303.15, 308.15, 313.15, 318.15 and 323.15 K respectively.

Molality(m) mol·kg-1	Urea				Thiourea
	ρ	ϕv		ϕv0	Molality(m) mol·kg-1		ρ	ϕv	ϕv0
T  = 298.15 K
0.00000	997.044				0.00000		997.044
0.14333	999.300	44.30		44.26	0.19984		1001.321	54.58	54.55
0.30767	1001.848	44.32			0.30720		1003.571	54.62
0.44066	1003.860	44.38			0.45193		1006.550	54.67
0.63874	1006.801	44.44			0.53601		1008.230	54.74
0.89270	1010.494	44.48			0.59753		1009.432	54.81
0.95956	1011.340	44.61			0.65270		1010.538	54.81
1.08983	1013.123	44.68			0.73880		1012.226	54.84
1.68355	1021.051	44.81			0.95090		1016.312	54.90
2.31850	1028.957	44.95			1.27989		1022.472	54.96
3.08261	1037.401	45.24			1.38780		1024.420	54.99
4.03605	1047.202	45.45			1.53355		1027.004	55.04
5.32037	1057.912	45.93
T  = 303.15 K
0.00000	995.644				0.00000	995.644
0.14333	997.857	44.65	44.60		0.19984	999.830		55.09	55.07
0.30767	1000.355	44.67			0.30720	1002.034		55.12
0.44066	1002.335	44.71			0.45193	1004.947		55.17
0.63874	1005.224	44.76			0.53601	1006.608		55.21
0.89270	1008.856	44.80			0.59753	1007.790		55.27
0.95956	1009.686	44.93			0.65270	1008.870		55.28
1.08983	1011.441	44.99			0.73880	1010.532		55.30
1.68355	1019.246	45.11			0.95090	1014.546		55.35
2.31850	1027.029	45.24			1.27989	1020.592		55.40
3.08261	1035.396	45.50			1.38780	1022.522		55.42
4.03605	1045.102	45.69			1.53355	1025.074		55.45
5.32037	1055.592	46.18
T  = 308.15 K
0.00000	994.025				0.00000	994.025
0.14333	996.201	44.96	44.90		0.19984	998.135		55.53	55.53
0.30767	998.652	44.99			0.30720	1000.295		55.57
0.44066	1000.606	45.01			0.45193	1003.162		55.60
0.63874	1003.454	45.05			0.53601	1004.793		55.64
0.89270	1007.028	45.09			0.59753	1005.956		55.70
0.95956	1007.847	45.21			0.65270	1007.018		55.70
1.08983	1009.576	45.27			0.73880	1008.654		55.72
1.68355	1017.263	45.39			0.95090	1012.612		55.75
2.31850	1024.941	45.51			1.27989	1018.572		55.79
3.08261	1033.177	45.76			1.38780	1020.457		55.82
4.03605	1042.735	45.95			1.53355	1022.968		55.85
5.32037	1053.154	46.41
T  = 313.15 K
0.00000	992.207				0.00000	992.207
0.14333	994.35	45.25	45.19		0.19984	996.249		55.94	55.95
0.30767	996.765	45.28			0.30720	998.375		55.98
0.44066	998.692	45.29			0.45193	1001.197		56.00
0.63874	1001.5	45.33			0.53601	1002.802		56.04
0.89270	1005.023	45.36			0.59753	1003.946		56.10
0.95956	1005.832	45.48			0.65270	1004.991		56.10
1.08983	1007.537	45.54			0.73880	1006.604		56.11
1.68355	1015.11	45.66			0.95090	1010.512		56.13
2.31850	1022.707	45.76			1.27989	1016.392		56.15
3.08261	1030.743	46.05			1.38780	1018.241		56.19
4.03605	1040.312	46.19			1.53355	1020.744		56.20
5.32037	1050.604	46.64
T  = 318.15 K
0.00000	990.204				0.00000	990.204
0.14333	992.318	45.51	45.45		0.19984	994.184		56.33	56.33
0.30767	994.712	45.50			0.30720	996.277		56.37
0.44066	996.605	45.54			0.45193	999.061		56.38
0.63874	999.378	45.58			0.53601	1000.644		56.41
0.89270	1002.858	45.61			0.59753	1001.772		56.47
0.95956	1003.658	45.73			0.65270	1002.800		56.47
1.08983	1005.341	45.79			0.73880	1004.391		56.48
1.68355	1012.837	45.89			0.95090	1008.234		56.51
2.31850	1020.334	46.00			1.27989	1014.024		56.53
3.08261	1028.285	46.28			1.38780	1015.872		56.54
4.03605	1037.802	46.40			1.53355	1018.319		56.57
5.32037	1047.947	46.85
T  = 323.15 K
0.00000	988.019				0.00000	988.019
0.14333	990.121	45.67	45.65		0.19984	991.950		56.67	56.67
0.30767	992.495	45.68			0.30720	994.018		56.69
0.44066	994.359	45.76			0.45193	996.765		56.72
0.63874	997.099	45.81			0.53601	998.321		56.76
0.89270	1000.539	45.84			0.59753	999.430		56.82
0.95956	1001.333	45.96			0.65270	1000.454		56.81
1.08983	1002.997	46.01			0.73880	1002.029		56.81
1.68355	1010.417	46.11			0.95090	1005.821		56.84
2.31850	1017.833	46.22			1.27989	1011.534		56.87
3.08261	1025.71	46.49			1.38780	1013.354		56.88
4.03605	1035.012	46.64			1.53355	1015.759		56.91
5.32037	1045.189	47.06

 

Table 2: Ultrasonic velocity, u/(m.s⁻¹) adiabatic compressibility, β_s/(10^-10·Pa^-1) apparent molar adiabatic compressibility, ϕ_k / (10^-14·m³·mol⁻¹. Pa^-1) limiting apparent molar volume, ϕ_k⁰(10^-14·m³·mol⁻¹.Pa^-1) and hydration number, n_H of urea and thiourea in aqueous solutions at 298.15, 303.15, 308.15, 313.15, 318.15 and 323.15 K respectively.

Molality(m)  mol·kg–1	Urea					Thiourea
	u	βs	ϕk	ϕk0	nH	Molality(m)  mol·kg-1		u	βs	ϕk	ϕk0	nH
T  = 298.15 K
0.00000	1496.79	4.477				0.00000		1496.79	4.477
0.14333	1500.58	4.444	-0.315	-0.281	2.8261	0.19984		1502.41	4.424	-0.215	-0.240	3.2544
0.30767	1504.74	4.408	-0.277		2.7597	0.30720		1505.40	4.397	-0.205		3.2255
0.44066	1507.98	4.381	-0.244		2.7075	0.45193		1509.40	4.361	-0.192		3.1870
0.63874	1512.63	4.341	-0.203		2.6374	0.53601		1511.54	4.341	-0.162		3.1405
0.89270	1518.65	4.291	-0.179		2.5834	0.59753		1513.27	4.326	-0.159		3.1303
0.95956	1519.94	4.280	-0.147		2.5439	0.65270		1514.56	4.314	-0.138		3.0957
1.08983	1522.84	4.256	-0.128		2.5107	0.73880		1516.97	4.293	-0.139		3.0854
1.68355	1535.46	4.154	-0.061		2.3785	0.95090		1522.17	4.247	-0.096		3.0031
2.31850	1547.98	4.056	0.002		2.2534	1.27989		1530.47	4.175	-0.067		2.9219
3.08261	1560.60	3.958	0.102		2.0886	1.38780		1533.07	4.153	-0.053		2.8920
4.03605	1577.33	3.838	0.158		1.9621	1.53355		1536.73	4.123	-0.043		2.8612
5.32037	1592.88	3.725	0.295		1.7523
T  = 303.15 K
0.00000	1509.18	4.410				0.00000	1509.18		4.410
0.14333	1500.58	4.380	-0.139	-0.123	2.6269	0.19984	1514.31		4.362	-0.018	-0.036	3.0364
0.30767	1504.74	4.347	-0.118		2.5835	0.30720	1516.99		4.337	0.000		2.9988
0.44066	1507.98	4.321	-0.091		2.5369	0.45193	1520.73		4.303	-0.003		2.9810
0.63874	1512.63	4.284	-0.061		2.4818	0.53601	1522.72		4.284	0.018		2.9440
0.89270	1518.65	4.238	-0.035		2.4251	0.59753	1524.25		4.271	0.026		2.9279
0.95956	1519.94	4.227	-0.009		2.3934	0.65270	1525.50		4.259	0.040		2.9035
1.08983	1522.84	4.205	0.009		2.3619	0.73880	1527.65		4.240	0.042		2.8886
1.68355	1535.46	4.110	0.068		2.2407	0.95090	1532.65		4.196	0.066		2.8311
2.31850	1547.98	4.018	0.122		2.1271	1.27989	1540.15		4.131	0.099		2.7469
3.08261	1560.60	3.926	0.211		1.9757	1.38780	1542.65		4.110	0.105		2.7253
4.03605	1577.33	3.813	0.259		1.8599	1.53355	1545.99		4.082	0.114		2.6957
5.32037	1592.88	3.707	0.385		1.6639
T  = 308.15 K
0.00000	1519.88	4.355				0.00000	1519.88		4.355
0.14333	1523.06	4.327	0.006	0.014	2.4600	0.19984	1524.60		4.310	0.141	0.134	2.8563
0.30767	1526.64	4.296	0.021		2.4248	0.30720	1527.07		4.287	0.157		2.8219
0.44066	1529.40	4.273	0.043		2.3835	0.45193	1530.44		4.256	0.162		2.7948
0.63874	1533.44	4.238	0.069		2.3343	0.53601	1532.29		4.239	0.178		2.7649
0.89270	1538.54	4.195	0.090		2.2846	0.59753	1533.64		4.226	0.190		2.7439
0.95956	1539.73	4.185	0.113		2.2569	0.65270	1534.83		4.215	0.198		2.7270
1.08983	1542.22	4.165	0.128		2.2288	0.73880	1536.78		4.198	0.201		2.7115
1.68355	1553.07	4.076	0.180		2.1173	0.95090	1541.48		4.156	0.213		2.6684
2.31850	1563.94	3.989	0.227		2.0137	1.27989	1548.48		4.094	0.237		2.5964
3.08261	1574.89	3.902	0.309		1.8731	1.38780	1550.78		4.075	0.243		2.5754
4.03605	1589.51	3.796	0.351		1.7662	1.53355	1553.85		4.049	0.252		2.5473
5.32037	1603.18	3.694	0.466		1.5838
T  = 313.15 K
0.00000	1528.95	4.311				0.00000	1528.95		4.311
0.14333	1531.88	4.286	0.130	0.133	2.3135	0.19984	1533.27		4.270	0.288	0.280	2.6859
0.30767	1535.18	4.257	0.143		2.2816	0.30720	1535.53		4.248	0.302		2.6543
0.44066	1537.75	4.234	0.159		2.2481	0.45193	1538.62		4.219	0.306		2.6303
0.63874	1541.51	4.202	0.180		2.2055	0.53601	1540.32		4.203	0.319		2.6035
0.89270	1546.26	4.162	0.197		2.1615	0.59753	1541.56		4.191	0.330		2.5843
0.95956	1547.34	4.152	0.220		2.1338	0.65270	1542.66		4.181	0.336		2.5697
1.08983	1549.66	4.133	0.233		2.1084	0.73880	1544.46		4.165	0.337		2.5567
1.68355	1559.84	4.049	0.277		2.0094	0.95090	1548.77		4.126	0.347		2.5172
2.31850	1569.92	3.967	0.320		1.9121	1.27989	1554.96		4.069	0.378		2.4386
3.08261	1580.16	3.886	0.397		1.7800	1.38780	1557.16		4.050	0.380		2.4241
4.03605	1593.84	3.784	0.431		1.6825	1.53355	1560.01		4.026	0.384		2.4011
5.32037	1606.69	3.687	0.537		1.5116
T  = 318.15 K
0.00000	1536.45	4.278				0.00000	1536.45		4.278
0.14333	1539.16	4.254	0.236	0.233	2.1865	0.19984	1540.44		4.239	0.408	0.398	2.5454
0.30767	1542.23	4.227	0.241		2.1631	0.30720	1542.51		4.219	0.424		2.5119
0.44066	1544.62	4.206	0.258		2.1314	0.45193	1545.33		4.191	0.430		2.4860
0.63874	1548.14	4.175	0.274		2.0950	0.53601	1546.92		4.176	0.439		2.4651
0.89270	1552.56	4.137	0.290		2.0538	0.59753	1548.02		4.166	0.453		2.4423
0.95956	1553.57	4.128	0.311		2.0281	0.65270	1549.08		4.156	0.454		2.4341
1.08983	1555.73	4.110	0.323		2.0043	0.73880	1550.72		4.140	0.456		2.4203
1.68355	1565.26	4.030	0.361		1.9141	0.95090	1554.52		4.104	0.475		2.3710
2.31850	1574.65	3.953	0.401		1.8222	1.27989	1560.09		4.052	0.506		2.2945
3.08261	1584.25	3.875	0.472		1.6989	1.38780	1561.99		4.035	0.511		2.2771
4.03605	1597.09	3.778	0.501		1.6086	1.53355	1564.60		4.012	0.515		2.2564
5.32037	1609.19	3.685	0.601		1.4472
T  = 323.15 K
0.00000	1542.50	4.254				0.00000	1542.50		4.254
0.14333	1545.03	4.231	0.314	0.317	2.0885	0.19984	1546.20		4.217	0.510	0.507	2.4253
0.30767	1547.83	4.206	0.332		2.0502	0.30720	1548.10		4.198	0.528		2.3896
0.44066	1550.13	4.185	0.339		2.0340	0.45193	1550.70		4.172	0.534		2.3639
0.63874	1553.41	4.156	0.355		1.9984	0.53601	1552.15		4.158	0.546		2.3411
0.89270	1557.53	4.120	0.370		1.9591	0.59753	1553.15		4.148	0.561		2.3177
0.95956	1558.49	4.112	0.389		1.9360	0.65270	1554.15		4.138	0.558		2.3134
1.08983	1560.50	4.094	0.401		1.9130	0.73880	1555.65		4.124	0.561		2.2996
1.68355	1569.41	4.018	0.436		1.8286	0.95090	1559.15		4.090	0.578		2.2532
2.31850	1578.21	3.945	0.473		1.7426	1.27989	1564.44		4.039	0.600		2.1899
3.08261	1587.22	3.870	0.538		1.6267	1.38780	1566.25		4.023	0.602		2.1755
4.03605	1599.29	3.777	0.567		1.5405	1.53355	1568.70		4.001	0.606		2.1566
5.32037	1610.67	3.688	0.659		1.3890

 

Limiting Apparent Molar Expansibility

The ϕ_v⁰ values are highly sensitive to temperature,¹³ and can be retrogression against the temp. using following equation,^14–16

where, T is the temperature in Kelvin, T_m is mean value of the studied temp. (here T_m = 310.65 K). The value of coefficients A, B & C were measured through polynomial fits and summarized in Table 3. The limiting partial molar expansibility (ϕ_E⁰), noted as a partial derivative of limiting partial molar volume with respect to temp., can be measured using the B & C parameters

described in above relation.

Calculated values of ϕ_E⁰ are shown in Table 3. with the fitting parameters of eq. 7. The Hepler’s constant (∂²ϕ_v⁰/∂T²)_p, provides detailed information on the hydration interaction in terms of structure making and breaking capacity of the solute, which can be obtained from equation (9)

Hepler^17-18 argued that a positive value of (∂²ϕ_v⁰/∂T²)_p is associated with structure making nature, whereas a negative value of (∂²ϕ_v⁰/∂T₂)_p is associated with a structure braking nature. It is apparent that the values of (∂²ϕ_v⁰/∂T₂)_p are negative for urea and thiourea in aqueous solution  are negative and (∂²ϕ_v⁰/∂T₂)_pvalue for thiourea is more negative than urea solution. Urea and thiourea solutions are attributed to the coordination of water molecules around urea and thiourea molecules through hydrophilic hydration. When the temperature is increased, the interactions between solute molecules become significant, and the hydrated water molecules around the hydrophilic groups are relaxed to bulk, and hence, urea and thiourea shows structure-breaking behavior. Probably due to bigger atomic size of sulfur, more interaction occurs between thiourea molecules and shows more structure breaking behavior. In hydration number observation, it’s observed that   hydration number of thiourea is higher than urea, this is due to the more interaction of water molecule detach from hydration sphere to bulk  results of more structure breaking behavior of thiourea.

Table 3: Fitting parameters of equation 7 for ϕ_v, limiting apparent molar expansibilities ( ϕ_E^O) and values of the Hepler’s Constant (∂²ϕ_v⁰/∂T₂)_p of urea and thiourea in aqueous solutions at 298.15, 303.15, 308.15, 313.15, 318.15 and 323.15 K respectively

/(10−7 m3 mol−1 K−1)
A	B	C	298.15 K	303.15 K		308.15 K		313.15 K		318.15 K		323.15 K		(∂2ϕv0 /∂T2)p
Urea
45.08	5.582	-0.636	0.717	0.654	0.590		0.526		0.463		0.399		-1.27
Thiourea
55.74	8.443	-0.845	1.056	0.971	0.887		0.802		0.717		0.633		-1.69

 

Conclusion

The densities and ultrasonic velocity of urea and thiourea in water were calculated at different temperatures & atmospheric pressure. From the measurements, apparent molar volumes (ϕ_v) apparent molar adiabatic compressibility (ϕ_k) limiting apparent molar volume (ϕ_v⁰) limiting apparent molar adiabatic compressibility (ϕ_k⁰) hydration number (n_H) and limiting apparent molar expansibility (ϕ_E⁰) are calculated. The ϕ_v values increase with an increase in temperature and concentration of urea and thiourea. The ϕ_v values of urea become more negative than thiourea, indicating that strong hydrophilic hydration of urea occurs together with the clustering of water in the bulk. Due to the strong hydrophilic hydration (strong hydrogen bond) of urea, ϕ_k values of urea increase than thiourea molecule. The ϕ_v⁰ values increase with an increase in temperature for both urea and thiourea. Solute-solvent interactions are more efficient for thiourea than urea because of more ability detachment of water molecule from thiourea. The ϕ_k⁰ values increase with an increase in temperature for both urea and thiourea. Because of more water molecule detachment from hydration sphere of thiourea, possibility of monomeric water molecule increases and ϕ_k⁰ values increase than urea molecule. The n_H values of urea and thiourea decrease with an increase in temp. & concentration of urea and thiourea. Due to the strong solute-solute interaction, more water molecule relaxes from hydration sphere of solute for both cases of temperature and concentration. More hydration number of thiourea are higher than urea because of increasing hydrophobic character for thiourea. From the expansibility measurement, it clearly observe that (∂²ϕ_v⁰/∂T₂)_p value for thiourea is more negative than urea solution. So, thiourea shows more structure breaking behavior than urea in solution.

Acknowledgments

Authors are thankful to the Dept. of Chemistry, University of Rajshahi, Bangladesh for providing laboratory facilities to carry out this work.

References

1. Hammes, G.; Schimmel, P. J. Am. Chem. 1967, 6028 (1960), 442–446.
2. Frank, H. S.; Franks, F. The J. of Chemical Physics .1968, 48(10), 4746-4757.
   CrossRef
3. Abu-Hamdiyyah, M. J. Phys. Chem. 1965, 69, 2720–2725.
   CrossRef
4. Subramanian, S.; Balasubramanian, D.; Ahluwalia, J. C. J. Phys. Chem. 1969, 73 (1), 266–269.
   CrossRef
5. Khatun, R. and Islam, N., Oriental J. of Chem, 2012, Vol. 28(1), 165-187.
6. Motin, M. a.; Biswas, T. K.; Huque, E. M. Phys. Chem. Liq. 2002, 40, 593–605.
   CrossRef
7. Krakowiak, J.; Wawer, J. J. Chem. Thermodyn. 2014, 79, 109–117.
   CrossRef
8. Tarlok, S. B.; Aashima, B.; Navalpreet, K. and Parampaul K. B. J. of Chem. & Eng. Data 2017, 62 (1), 20-34
   CrossRef
9. Khatun, M. R.; Islam, M. M.; Rima, F. R.; Islam, M. N. J. Chem. Eng. Data, 2016, 61 (1), 102–113
   CrossRef
10. Doyel, M. B.; Sudhakar, S. D. and Sangesh, P. Z. The J. of Chem Therm. 2016, 101, 207-220
    CrossRef
11. Latha, M.; Vijay, M. T.; Sudhakar, S. D.; Dinesh, W. D.; Santosh, P. J. The J. of Chem. Therm. 2017, 112, 166-177
12. Burakowski, A.; Gli, J. Hydration Numbers of Nonelectrolytes from Acoustic Methods. Chem. Rev. 2012, 112, 2059–2081.
    CrossRef
13. Rima, F. R.; Islam, M. M.; Islam, M. N. J. Chem. Eng. Data 2013, 58 (11), 2991–2997.
    CrossRef
14. Hakin, A. W.; Copeland, A. K.; Liu, J. L.; Marriott, R. A.; Preuss, K. E. Densities, J. Chem. Eng. Data 1997, 42 (1), 84–89.
    CrossRef
15. Li, Y.; Li, Y.; Wang, F.; Ren, B. J. Chem. Thermodyn. 2013, 66, 14–21.
    CrossRef
16. Pal, A.; Chauhan, N. J. Chem. Thermodyn. 2012, 54, 288–292.
    CrossRef
17. Hepler, L. G. Can. J. Chem. 1969, 47 (24), 4613–4617.
    CrossRef
18. Kabir, M. H.; Nath, R. K.; Hossain, M. K.; Hyder, M. K. M. Z., Oriental Journal of Chemistry 2018, 34(1), 196-202.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.