Vibrational Spectra of Copper Tetramesityl Porphyrin using Vibron Model

Introduction

Group theory is a well known tool that simplifies the process of obtaining a variety of information about molecules and their symmetries. Molecules are classified according to their symmetry properties and from that one can identify, the molecular symmetry point group. The molecular symmetry point group of Metalloporphyrins is D_4h, which contains the principal C_n axis, n perpendicular C₂ axis, and the horizontal plane of symmetry.

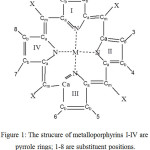Figure 1: The strucure of metalloporphyrins I-IV are pyrrole rings; 1-8 are substituent positions. X positions are (=CH-) bridges Click here to View figure

 

In 2008, Karumuri et al, applied Vibron model for coupled anharmonic oscillators to describe the stretching vibrations of medium size molecules and calculated vibrational spectra of nickel octaethyl Porphyrins for the stretching mode C_m – H. In the intervening years extended this model to calculate stretching vibrational frequencies of nickel tetraphenyl porphyrin and copper octaethyl porphyrin for different vibrational bands [1-9].

Vibron model for Metalloporphyrins

The general calculation procedure of vibrational spectra of Metalloporphyrin by Vibron model discussed here [10, 11]. The Hamiltonian for the polyatomic molecules is of the form

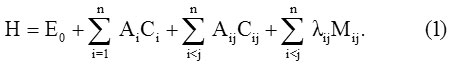
Here i vary from 1 to n for n stretching bonds and (A_i, A_ij, λ_ij)are algebraic parameters, which are determined by spectroscopic data. Where  C_i is an invariant operator (uncoupled bonds) with eigenvalues

Diagonal matrix elements of the invariant operator C_ij (coupled bonds) and diagonal and non-diagonal matrix elements of Majorana operator M_ij obtained from the following relations,

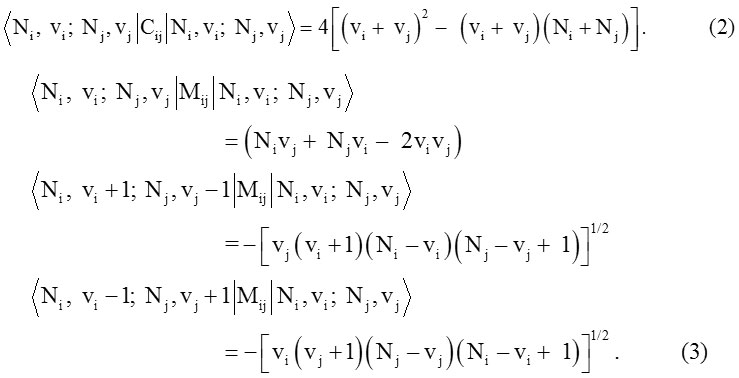
Where V_i (i = 1,2,3,…) are vibrational quantum numbers.

The vibron number N_i (i = 1,2,3,…) for stretching bonds of molecule will be calculated by the following relation

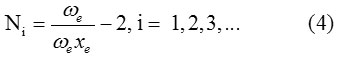
Where ω_e and ω_e x_e are spectroscopic constants. The initial guess value for the parameter A_i  is obtained by using the energy equation for the single-oscillator fundamental mode, which is given as,

Initial guess for A_ij may be taken as zero. The parameter λ_ij obtained from the relation

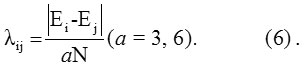
Results

Table 1: Vibrational spectra of Cu(TMP)

Symmetry Species	Vibrational mode	Vibrational frequencies (cm-1)
A1g	(Cm-C)	1235.04348
B2g	(Cm-C)	1247.03267
Eu	(Cm-C)	1256.90364
A1g	(Cb-H)	1470.00431
B2g	(Cb-H)	1476.05321
Eu	(Cb-H)	1470.87451

 

Table 2: Algebraic parameters

Algebraic parameters	Cm – C	Cb – H
A	-2.19234 cm-1	-5.90923 cm-1
Aij	-0.98232 cm-1	-2.92012 cm-1
λij (a = 3)	0.02421 cm-1	0.80834 cm-1
λij (a = 6)	0.20091 cm-1	0.03421 cm-1
N (Dimensionless)	140	44

 

Conclusion

In this paper we have calculated the vibrational frequencies of copper tetramesityl porphyrin (Cu(TMP))  for the stretching modes (C_m-C) and (C_b-H).

References

1. Karumuri, S. R. Indian J. Phys. 2012, 86(12), 1147-1153.
   CrossRef
2. Karumuri, S. R.; Sekhar, J.V.; Sreeram, V.; Rao, V. U.M.; Rao, M.V.B.; J Mol Spectrosc. 2011, 269, 119-123.
   CrossRef
3. Karumuri, S. R.; Srinivas, G.; Sekhar, J.V.; Sreeram, V.; Rao, V. U.M.; Srinivas, Y.; Babu, K.S.; Kumar, V.S.S.; Hanumaiah, A.;  Chin Phys B. 2013, 22(9), 090304 (1-8).
4. Karumuri, S. R.; Sarkar, N.K.; Choudhury, J.; Bhattacharjee, R.; Mol. Phys. 2008, 106(14), 1733-1737.
   CrossRef
5. Karumuri, S. R.; Sarkar, N.K.; Choudhury, J.; Bhattacharjee, R.; Chin Phys Lett. 2009, 26(9), 093301 (1-4).
6. Karumuri, S. R. Chin Phys Lett. 2010, 27(10), 103301 (1-4).
7. Karumuri, S. R. J Mol Spectrosc. 2010, 259, 86-92.
   CrossRef
8. Karumuri, S R. Eur. Phys. J. 2015, 69, 281.
9. Karumuri, S. R.;  Sravani, K.G.; Mol. Phys. 2016, 114(5), 643-649.
   CrossRef
10. Iachello, F.; Levine, R. D. Oxford University Press, Oxford. 1995.
11. Oss, S. Adv. Chem. Phys. 1996, 93, 455- 649.

---

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.