Thermodynamic Study and Mathematical Modeling of Adsorption of Co2+ ions on Biopolymers based of Sugarcane Bagasse
S. Elanza1 , H. Taouil2, 3, A. Amine4, M. Doubi2, A. Lebkiri1 and El. Rifi1
, H. Taouil2, 3, A. Amine4, M. Doubi2, A. Lebkiri1 and El. Rifi1
1Laboratory of Organic Synthesis and Process of Extraction, Faculty of Sciences, University Ibn Tofail, Kentia, Morocco.
2Laboratory of Materials, Electrochemistry and Environment, Faculty of Sciences University Ibn Tofail kénitra, Morocco.
3Laboratory of Analytical Chemistry and Physical Chemistry of Materials. Hassan II University of Casablanca.
4Laboratory of Condensed Matter and Renewable Energy. Faculty of Sciences and Technology. Hassan II, University.
Corresponding Author E-mail: elanza.said@hotmail.com
DOI : http://dx.doi.org/10.13005/ojc/330667
The main objective of this work is to study the thermodynamic study and mathematical modeling of the adsorption of Co2+ ions on biopolymers based of sugarcane bagasse (SCB) for to approximately the nature of the adsorption. The together of results obtained show that the adsorption process is favorable for a chemisorption and monolayer. Also, the adsorption process is expressed by the second order kinetic law. Thus the negative values of ΔG° and the positive values of ΔH° opt for an endothermic and spontaneous process. Also, the positive values of ΔS° indicate the increase in the randomness at the solid / liquid interface during the adsorption of the Co2+ metal ions.
KEYWORDS:Adsorption Of Co2+; SCB; Mathematical Modeling; Kinetic Models; Adsorption Isotherms
Download this article as:| Copy the following to cite this article: Elanza S, Taouil H, Amine A, Doubi M, Lebkiri A, Rifi E. Thermodynamic Study and Mathematical Modeling of Adsorption of Co2+ ions on Biopolymers based of Sugarcane Bagasse. Orient J Chem 2017;33(6). |
| Copy the following to cite this URL: Elanza S, Taouil H, Amine A, Doubi M, Lebkiri A, Rifi E. Thermodynamic Study and Mathematical Modeling of Adsorption of Co2+ ions on Biopolymers based of Sugarcane Bagasse. Orient J Chem 2017;33(6). Available from: http://www.orientjchem.org/?p=41023 |
Introduction
In recent years, the adsorption of heavy metals into solutions on natural adsorbents has a to been a considerably developed through several research works, thanks to their metal recovery efficiencies and the saving of equipment [1-9].
The process of adsorption can be divided into two mechanisms that can occur independently or simultaneously:
Physical adsorption is due to electromagnetic forces between molecules of the adsorbent and the adsorbate, often referred to as van deer Waals forces. These attractions lead to molecular condensation where substances adsorbed remain on the surface or are irreversibly bound [10].
Chemical adsorption relies on a chemical bond which is stronger than a physical bond between the solid and the adsorbed species. This union leads to the release of heat and the formation on a monomolecular layer of the adsorbate [11]. The strong interaction produced can be irreversible.
In this work, we have modeled the experimental results obtained during the study of the adsorption of the metal ions Co2+ by the sugarcane bagasse for to approximately the nature of the adsorption [12].
We studied three kinetic models: First order kinetic model, second order kinetic model and Elovich kinetic model [13-15].
Also, we studied three models of adsorption isotherms: Freundlich model, Langmuir model and Temkin model [16-18].
Materials and Methods
Preparation of the Adsorbent
The sugarcane bagasse is made up mainly by natural polymers (biopolymers) such as, the cellulose whose monomer is the glucose, the hemicellulose which is a copolymer whose principal reason is composed of xylose connected with glucose and arabinose [19], and the lignin which is a three-dimensional polymer, its pattern is constituted mainly by three different monomers such as, coniferyl alcohol, paracoumaryl alcohol and sinapyl alcohol [20].
The sugarcane bagasse is the residue which remains after the extraction of sugar contained in sugarcane; it was dried with the air, under the action of the solar rays, then crushed and tamised so as to obtain homogeneous materials for the experimental achievements, and the fraction of granularity of very low diameter.
Preparation of Adsorbate
The metal solutions of cobalt are prepared by dissolving of the cobalt chloride salt hydrated (CoCl2, 3H2O) in distilled water. The pH of each solution was adjusted by hydrochloric acid (HCl) and the sodium hydroxide (NaOH).
Kinetics Models
First Order Kinetic
The first order kinetic model expressed by the Lagergren equation.
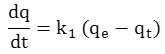
After integration between t = 0 and t, qt = 0 and qt we obtain the linear form:
ln (qe– qt) = ln qe – k1t
The course of the curve ln (qe – qt) = f (t) gives a straight line with the slope equal -k1 and the ordinate at the origin equal to ln (qe).
qt and qe : The adsorption capacities at time t and the adsorption equilibrium.
k1 (min-1): speed constant of the process of extraction of the first order.
Second Order Kinetic
The kinetic model of second order is expressed by the equation of HO and MCKAY.
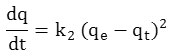
After integration between t = 0 and t, qt = 0 and qt we obtain the linear form:
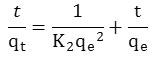
The course of the curve t/qt = f (t) gives a straight line with the slope equal 1/qe and intercept equal to
![]()
k2 (g min-1mg-1): speed constant of the adsorption process of the second order.
Elovich Model
The kinetic model of Elovich was also applied to the experimental results. This model is one of the most used models to verify and describe the adsorption of chemisorption.
The kinetic model of Elovich is expressed by the following equation.
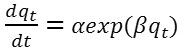
After integration this equation we obtain the linear form:
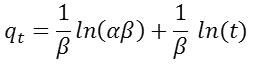
The course of the curve qt = f (lnt) gives a straight line with the slope equal
![]()
and intercept equal to
![]()
The constant α (mg g-1 min-1) is the initial rate of adsorption and β (g mg-1) is the desorption constant related to the extent of surface coverage and activation energy for chemisorption.
Adsorption Isotherm Models
Model of Freundlich
The Freundlich model is based on the hypothesis of a heterogeneous surface of the adsorbent with an exponential distribution of the active sites as a function of the adsorption energies.
The Freundlich model is expressed by the following equation:
qe = KF Ce1/n
The linear form of this model is given by the following equation:
lnqe = lnKF+ 1/n lnCe
The plot of the linear form lnqe = f (Ce) gives a line of slope 1 / n and the ordinate at the origin equal à lnKF.
KF and
![]()
are constants of Freundlich related at the adsorption capacities. If
![]()
the adsorption is linear, if
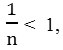
the adsorption is favorable, and if
![]()
the adsorption is unfavorable.
Model of Langmuir
The Langmuir model makes it possible to determine if a monolayer is adsorbed and if there is no interaction between the adsorbed molecules. The Langmuir equation is valid for only one monolayer adsorbed with a well defined number of uniform and energetically identical adsorption sites according to the following relation:
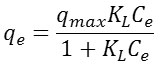
The linear form of this model is given by the following equation:
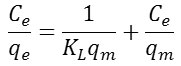
The plot of the linear form
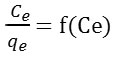
gives a straight line of slope
![]()
and the ordinate at the origin equal to
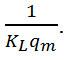
qm is the quantity needed to cover the entire surface with a monolayer of adsorbed substance, and KL is the constant of Langmuir isotherm. RL is the Langmuir separation factor or the equilibrium parameter was used to give an indication on adsorption. 0 <RL <1, the adsorption is favorable, RL> 1 the adsorption is unfavorable, RL = 0 the adsorption is irreversible and RL = 1 the adsorption is linear.
RL is terminated by the following relation:
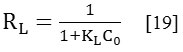
With Co (mg/g) is the initial concentration, and KL is the constant of Langmuir.
Model of Temkin
The Temkin isotherm assumes that the decrease in heat of adsorption is linear and that the adsorption is characterized by a uniform distribution of binding energies. The Temkin model is expressed by the following equation:
![]()
The linear form of this model is given by the following equation:
qe = B Ln KT + B Ln Ce With,
![]()
KT: constant of equilibrium of Temkin (l / mg).
B = ΔQ: variation of energy of the adsorption (kj / mol).
R: is the perfect gas constant (8.314 J mol-1K-1) and T the temperature in K. The plot of the linear form qe = f (Ce) gives a straight line of slope B and the ordinate at the origin equal to B lnKT.
Thermodynamic Study
The thermodynamic parameters, such as the Gibbs free energy (ΔG°), the enthalpy (ΔH°) and the entropy (ΔS°) were calculated using the following equations:
ΔG° = – RT Ln Kc
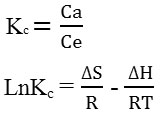
Kc is the equilibrium constant; Ca is the concentration in the solid phase at equilibrium (mg L-1). Ce is the concentration in the solution at equilibrium (mg l-1); R is the ideal gas constant (8.314J mol-1 K-1). ΔH° and ΔS° were obtained from the slope and intercept of LnKc versus 1 / T. the temperature (T) used are: 25°C (298K), 36°C (309k), 45°C (318K).
Results and Discussions
Kinetic Models
Kinetic Models of First and Second Order
The results of the study of the kinetic model of first and second order during the adsorption of the Co2+ ions on the SCB are presented in fig 1 and fig 2.
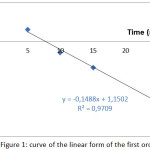 |
Figure 1: curve of the linear form of the first order |
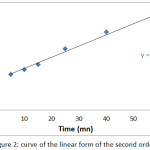 |
Figure 2: curve of the linear form of the second order |
The table 1 gathers the correlation and the constant kinetics of extraction for the two models.
Table 1: Parameters of kinetic models of first and second order
| Models | First order | Second order | ||||||
| Kinetic paramèters | K1 | qexp (mg/g) | qcal (mg/g) | R2 | K2 | qexp(mg/g) | qcal (mg/g) | R2 |
| 0.1488 | 2.58 | 3.15 | 0.9709 | 0.014 | 2.58 | 2.62 | 0.9912 | |
The results in this table show that the correlation coefficient R2 given by the second order kinetic model is greater than the first order, also the binding capacity calculated at equilibrium (qcal) for the second order kinetic model is very close to the experimental binding capacity at equilibrium (qexp), therefore we can deduce that the extraction kinetics of Co2+ by SCB is expressed by the second order kinetic.
Kinetic Model of Elovich
The results of the study of the kinetic model of Elovich during the adsorption of the Co2+ ions on the SCB are presented in fig 3.
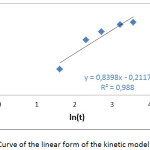 |
Figure 3: Curve of the linear form of the kinetic model of Elovich |
The table 2 gathers the correlation and the parameters kinetics of Elovich model.
Table 2: parameters of kinetic model of Elovich
| Parameters of Elovich | α (mg g-1 min-1) | β (g mg-1) | R2 |
| 0.653 | 1.19 | 0.988 |
The value of R2 is close to unity, R2> 0.98, which probably means that the adsorption of Co2+ on the SCB is chemisorption.
Models of Adsorption Isotherms
Model of Freundlich
The results of the study of the linear form of the Freundlich model during the adsorption of the Co2+ ions on the SCB are shown in fig 4.
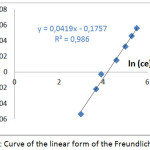 |
Figure 4: Curve of the linear form of the Freundlich model |
The table 3 summarizes the parameters of the Freundlich model during the adsorption of the Co2+ ions on the SCB.
Table 3: Parameters of model of Langmuir
| 1/n | KF (mg/g) | R2 |
| 0.0419 | 0.839 | 0.9696 |
According to these results, it can be seen that the correlation coefficients R2 are close to the unity, and 1/n < 1. Therefore the adsorption process is favorable and the surface of the SCB material is heterogeneous.
Model of Langmuir
The results of the study of the linear shape of the Langmuir model during the adsorption of the Co2+ ions on the SCB are shown in fig 5.
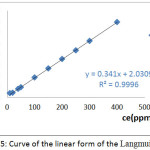 |
Figure 5: Curve of the linear form of the Langmuir model |
The table 4 summarizes the parameters of the Langmuir model during the adsorption of the Co2+ ions on the SCB.
Table 4: Parameters of model of Langmuir
| qm cal (mg.g-1) | qm exp (mg.g-1) | KL (l/mg) | RL | R2 |
| 2.93 | 2.88 | 0.168 | 0.0146 | 0.9996 |
The results obtained show that all the correlation coefficients R2 are close to the unity, 0 < RL <1 and the calculated maximal fixing capacities (qm cal) are very close to the maximum experimental capacities (qm exp). Therefore, the adsorption process is favorable and the surface of the SCB material is heterogeneous.
Model of Temkin
The results of the study of the linear shape of the Temkin model during the adsorption of the Co2+ ions on the SCB are shown in fig 6.
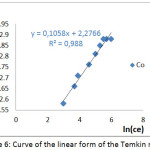 |
Figure 6: Curve of the linear form of the Temkin model |
The table 5 regroup the parameters of model of Temkin during the adsorption of the Co2+ ions on the SCB.
Table 5: Parameters of model of Temkin
| KT (l/mg) | B | ∆Q (Kj/mol) | R2 |
| 2.497 | 0.1058 | 23.417 | 0.988 |
The results of this table show that all the correlation coefficients R2 are close to unity. Therefore, it can be concluded that the adsorption is monolayer and the distribution of the binding energies is uniform.
Thermodynamic Study of the Adsorption of Co2+ on the SCB
The results of the thermodynamic study of the adsorption of Co2+ ions on the SCB are shown in the fig 7.
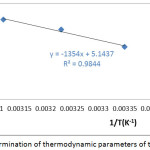 |
Figure 7: Determination of thermodynamic parameters of the adsorption Click here to View figure |
The table 6 regroup the thermodynamic parameters of the adsorption of Co2+ ions on the SCB.
Table 6: The thermodynamic parameters of the adsorption
| T (0K) | ∆G0 (KJ mol-1) | ∆H0 (KJ mol-1) | ∆S0 (J mol-1k-1) | R2 |
| 298 | -1.479 | 11.257 | 72.79 | 0.9844 |
| 309 | -2.037 | |||
| 318 | -2.399 |
The results of the thermodynamic study of the adsorption of metal ions Co2+ on SCB, show that the values positive of ΔH0 which indicates the endothermic nature of the adsorption. Also, the negative values of the ΔG0 show that the adsorption process was spontaneous. The variation of entropy (ΔS0) is a measure of disorder. The transformations spontaneous go in the direction of an increase in disorder. In our case, the positive values of ΔS0 indicate the increased randomness in the solid / liquid interface during the adsorption of metal ions Co2+ on the SCB.
Conclusion
The mathematical modeling of the adsorption of Co2+ ions on sugarcane bagasse (SCB) was studied. The results obtained give the following conclusions:
The study of kinetic models shows that, the adsorption process is expressed by the second order kinetic law.
The study of the adsorption isotherm models show that, the adsorption process is favorable, chemisorption, monolayer, the surface of the SCB material is heterogeneous and the distribution of the binding energies is uniform.
The thermodynamic study of the adsorption shows that, the negative values of ΔG0 show that the adsorption process occurs spontaneously and the positive values of ΔH0 show that the process is endothermic. Also the positive values of ΔS0 indicate increasing the randomness at the solid / liquid interface during the adsorption of Co2+ ions on the SCB.
Acknowledgements
Thanks are due to the Laboratory of the National office of Hydrocarbons and Mines (ONHYM) for analyzing samples and the professor Bruce Spittle.
References
- S. Elanza, A. Lebkiri, E.H. Rifi, J. Hmimou, M. Lebkiri, Y. Essaadaoui, International Journal of Scientific & Engineering Research, 2015, 5, 1661-1667.
- S. Elanza, A. Lebkiri, J. Hmimou, E.H. Rifi, Mor. J. Chem. 2015, 3, 669-674.
- S. Elanza, A. Lebkiri, E.H. Rifi, Mor. J. Chem. 2015, 3, 40-46.
- J. Hmimou, S. Elanza, E.H. Rifi, A. Lebkiri, M. Ebn Touhami, Z. Hatim, Mor. J. Chem. 2015,3, 263-271.
- S. Elanza, A. Lebkiri, S. Marzak, E.H. Rifi, M. Lebkiri, C. Satif, J. Mater. Environ. Sci. 2014,5, 1591-1598
- Elanza Said, Lebkiri Ahmed, Rifi Elhosseine, Ibn Ahmed Said, Science Lib Editions Mersenne, 2011, 3, 110402.
- Kiptoo J. K., Ngila J. C., Silavwe N. D. Microchimica Acta, 2008,160, 211-218.
CrossRef - Calderon V., Serna F., Garcia F., De La Pena J J. L. App. Poly. Sci. 2007, 106, 2875-2884.
CrossRef - Ayata S., Kaynak I., Merdivan M. Environmental monitoring assessment, 2009, 153, 333-338.
CrossRef - Treybal, R.E. Mass Transfer Operations. McGraw Hill, New York. 1981.
- Eckenfelder Jr. W.W. Granular carbon adsorption of toxics. In: Allen, P.W., Eckenfelder, Jr., W.W. (Eds.), Toxicity Reduction of Industrial Effluents. Van Norstrand Reinhold, New York, 1990, .203–228.
- S. Elanza, H.Touil. A. Lebkiri, E.H. Rifi, International Journal of Scientific & Engineering Research, 2016, 7, 845-849.
- S. Lagergren, Kungliga Svenska Vetenskapsakademiens Han-dlingar, 1898, 24,1-39.
- Y. Ho, A. E. Ofomaja, Journal of Hazardous Materials 2006, 129, 137-142.
CrossRef - N. H. Turner, Journal of Catalysis, 1975, 36, 262-265.
CrossRef - H. Freundlich, Ueber die Adsorption in Loesungen, Zeitschrift für physikalische Chemie, 1907, 57, 385-471.
- I. Langmuir, The constitution and fundamental properties of solids and liquids, Journal of the American Chemical Society, 1916, 38, 2221-2295.
CrossRef - M. I. Temkin, V. Pyzhev, Kinetics of ammonia synthesis on promoted iron catalyst, Acta Phys. Chim. USSR, 1940, 12, 327-356.
- Sun J.X., Sun X.F., Sun R.C., Sun Y.Q. Fractional extraction and structural characterisation of sugarcane bagasse hemicelluloses carbohydrate polymers, 2004.56, 195-336.
- Amen Chen C., Pakdel H., Roy C. Production of monomeric phenols by thermochemical conversion of biomas. Bioresourse technology, 2001, 79, 277-299.

This work is licensed under a Creative Commons Attribution 4.0 International License.









