Kinetic Evaluation of Influence of Surfactant on Oxidation Reaction of Carboxylic Acid by Molecular Hmn O₄

Vandana Sharma¹, Kirti Yadav² P. C. Choyal³ and V. R. Chourey⁴

¹Department of Chemistry Govt. Holkar Science Autonomous College Indore, India.

²Kashutrba Gram Rural College, Indore, India.

³Govt. P.G. College, Dhar, India.

⁴Govt. Holkar Science Autonomous College Indore, India.

Corresponding author Email: vandana203@gmail.com

DOI : http://dx.doi.org/10.13005/ojc/330662

ABSTRACT:

Surfactant catalyzed oxidation of n-butyric acid has been carried out for kinetic and mechanistic investigations in sulphuric acid medium by molecular HMnO₄ species. Reaction has also been observed in absence of surfactant.The substrate oxidised in two steps in which first step is slow in comparision to second step which fast one. Micelles of surfactant work as positive catalyst. Substrate and oxidant both follows first order kinetics.Different hypotheses have been applied related to the acidity function to arrive the correct reaction mechanism. Number of moles between substrate and oxidant has also been determined. Temperature variation parameters presented in terms of activation parameters, those are found in prescribed limit. Mechanism for reaction has been suggest on the basis of parameters observed.

KEYWORDS:

Kinetics; Micelles surfactant; Oxidation; acidic permanganate ion

Download this article as: 

Copy the following to cite this article: Sharma V, Yadav K, Choyal P. C, Chourey V. R. Kinetic Evaluation of Influence of Surfactant on Oxidation Reaction of Carboxylic Acid by Molecular HmnO4. Orient J Chem 2017;33(6).

Copy the following to cite this URL: Sharma V, Yadav K, Choyal P. C, Chourey V. R. Kinetic Evaluation of Influence of Surfactant on Oxidation Reaction of Carboxylic Acid by Molecular HmnO4. Orient J Chem 2017;33(6). Available from: http://www.orientjchem.org/?p=40540

Dependency of reaction rate on permanganate concentration and potassium dichromate

Dependency of reaction rate on permanganate has been studied by varying is initial concentration at constant concentration of other reactants. It shows that rate constant does not alter with variation in oxidant concentration. The plot of log of optical density i.e. log(a-x) and time exhibit double stage process each being linear. It confirms first order kinetics with respect to permanganate (figure-1.1).

The oxidation has also been carried out by potassium dichromate from the comparative point of view. In this case it has been observed that the reaction is single stage process (figure-1.2).

From the comparative point of view it has been confirmed that oxidation by dichromate is possible at very low concentration of sulphuric acid in comparision to the oxidation by permanganate. It has also been observed that the rate of oxidation by dichromate is comparatively fast than by permanganate.

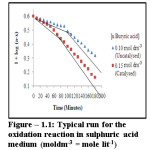Figure 1.1: Typical run for the oxidation reaction in sulphuric acid medium (moldm-3 = mole lit-1) Click here to View figure

Figure 1.2: variation of [Dichromate]  Click here to View figure

 

Study of variation of substrate concentration

To study the variation of substrate concentration experiments were performed at 308 K with different initial concentration of substrate, other reactants concentration were kept constant. The rate for both in uncatalyzed and catalyzed reaction was found to increase with the concentration of substrate. Table 1.

Table 1 :Variation of n-butyric acid concentration (Uncatalyzed and Catalyzed)

[H2SO4] = 4.0 mole lit-1  Temperature = 308K					[KMnO4] = 1.0×10-3 mole lit-1 [NaLS] = 1.0×10-4 mole lit-1
	Uncatalyzed					Catalyzed
n-butyric acid mole lit-1	× 10-3Min-1		× 10-3Min-1			× 10-3Min-1		× 10-3Min-1
	By Differential method	By Graphical method	By Differential method	By Graphical method		By Differential method	By Graphical method	By Differential method	By Graphical method
0.05	1.15	1.22	2.81	2.92		1.26	1.28	2.46	2.53
0.10	2.07	2.01	5.10	5.06		2.32	2.28	4.42	4.28
0.15	3.12	3.06	7.50	7.45		3.53	3.54	6.48	6.47
0.20	4.03	4.10	10.12	9.96		4.61	4.72	8.67	8.65
0.25	5.00	4.95	12.40	11.36		5.69	5.64	11.06	11.11
0.30	5.80	5.53	15.08	13.94		6.39	6.33	12.51	11.74

Plot of logarithm of [n-butyric acid] with logarithm of rate constant (k₁ and k₁”) give straight line (figure-1.3) approximately of unit gradient in both the stages. These show that the n-butyric acid follows first order kinetics for each stages and plots of 1/k₁, 1/k₁” against 1/Substrate concentration (i.e. Michaelis-Menten plots) give straight lines (figure-1.4) passing through the origin for both the first and second stages.These again exhibit the first order dependence of reaction rate on n-butyric acid for both the stages. It also confirms that substrate and oxidant are not forms any intermediate complex ¹⁸. However if any complex is formed, its formation constant would be extremely small¹⁹.

Effect of the variation of the [H⁺] concentration

The reaction was studied at different sulphuric acid concentrations, keeping the constant concentration of n-butyric acid, potassium permanganate and sodium lauryl sulphate. The variation of the [H⁺] concentration on the reaction rate has been investigated. The experimental results obtained are presented in table 2.

Table 2 : Study of change in the [H⁺] concentration

[n-butyric acid] = 0.20 mole lit-1 Temperature = 308K			[KMnO4] =1.0 × 10-3 mole lit-1   [NaLS] = 1.0 ×10-4 mole lit-1
[ H+] mole lit-1	-H0			×10-3 Min-1	×10-3 Min-1
2.0	0.84	0.043		1.20	2.41
2.5	1.12	0.063		1.33	3.25
3.0	1.38	0.085		1.63	4.75
3.5	1.62	0.111		2.04	6.20
4.0	1.85	0.142		2.44	8.67

Applicability of Zucker-Hammett, Bunnett and Bunnett-Olsen hypotheses

Different hypotheses have been applied to investigate the role and activity of H⁺ ion on the oxidation reaction. In order to determine correlation between H⁺ concentration of rate of reaction, the two Zucker-Hammett²⁰ plots i.e. the plot of (log k₁(k₁^”)  against – H₀) and the other plot of (log k₁(k₁^”) against log [H⁺]) linearly of above plots exhibit the acid catalysed nature of reaction. However, slope values of Zucker-Hammett plot are not unity as required. Deviation from the ideal slope value of unity suggests that the water molecule may be involved in some way in the slowest rate determining step. Since the ideal slope values (i.e. unity) of two Zucker-Hammett plots are not obtained hence the Bunnett’s plots²¹ i.e. the Bunnett relationships (log [rate constant] + log [H_o]) against log a_H2O, log ([rate constant] – log[H⁺]) against loga_H2O and (log [rate constant] – log[H⁺] – H_o) against log a_H2O have been obtained. In the same way the Bunnett-Olsen plot²² i.e. the plot of linear free energy relationship, i.e. (log [rate constant] + H₀) against (H₀ + log [H⁺]) has also been obtained. As per Bunnett and Bunnett-Olsen empirical observations the reported slope values of these plots confirms that in the [H⁺] catalyzed reactions rate determining step involves the H₂O molecule. The role of the H₂O molecule is confirmed as proton abstracting agent in the rate determining step. The slope values of two Bunnett plots i.e. ω and ω* and of one Bunnett-Olsen plots ‘ф’ have been reported in the table 3. The values of -H₀ and a_H2O have been taken from Bunnett, Paul and Long²³ respectively.

[n-butyric acid] = 0.20 mole lit-1 Temperature = 308K			[KMnO4] = 1.0 × 10-3 mole lit-1  [NaLS] = 1.0 ×10-4 mole lit-1
S.No	Correlation	Parameters	Slope value (H2SO4 medium)
			I stage	II stage
1.	Zucker-Hammett plot
(a)	(log Rate constant) against -H0	Slope	0.316	0.553
(b)	(log Rate constant) against log [H+]	Slope	1.23	1.58
2.	Bunnett’s plots
(a)	(log Rate constant + H0) against	(ω)	-6.88	-4.51
(b)	(log Rate constant – log [H+]) against	(ω*)	0.250	2.62
(c)	(log Rate constant] – log [H+] –H0) against	Slope	10.37	12.74
3.	Bunnett – Olsen plot (L.F.E.R)
(a)	(log Rate constant +H0)  against (H0 + log [H+])	(ф )	0.972	0.636

NaLS concentration variation

Effect of variation of concentration sodium lauryl sulphate (NaLS) has been studied keeping the other reactants constant at given constant temperature.

It is clear that the pseudo first order rate constant for the given concentration range of NaLS increases with the increase in NaLS Concentration (Table 4). In the present study, it has been suggested that the formation of premicellar aggregates is responsible for the miceller catalysis.

The catalysis by the concentration of micelle which is below their cmc (i.e. critical micelles concentration) is termed as premiceller catalysis as reported in the literature ^24-26. It has been determined graphically by plotting a Piszkiewicz graph between log [k_obs – k_o] / [k_m – k_obs] and log [NaLS]. Here k_o is the velocity constant in absence of NaLS, k_obs is the velocity constant at different NaLS concentration, while k_m is the maximum velocity constant in presence of NaLS used. The range of variation of NaLS were kept between from 5.0×10^-4 to 9.0 × 10^-4 mol liter^-1. Its maximum concentration used is 9.0 × 10^-4 mole lit^-1. This is well below the reported cmc of sodium lauryl sulphate as reported in the literature is 8.1× 10^-3 mole lit^-1 at 298K. This confirms that the observed phenomenon is a case of premiceller catalysis.

The slope value ‘n’ obtained from this graph which is a good straight line for first and second stages are 1.86 and 2.01.These are between the expected value i.e. between 1 to 6 which is for premiceller catalysis. In the case of miceller catalysis this value should be more than 20. This is according to the binding parameters as suggested by Piszkiewicz²⁷.

The results have been reported in the table 4 for both the stages. The ‘n’ value of positive cooperativity also supports the substrate promoted micellization which is analogous to positive cooperativity in case of enzymatic reactions^28-30.

[n-butyric acid] = 0.10 mole lit-1 [H2SO4]  = 4.0 mole lit-1			[KMnO4] = 1.0 × 10-3 mole lit-1 Temperature = 308K
[NaLS] mole lit-1	×10-3 Min-1	×103        litre mol-1Min-1		×103 Min-1	×103          litre mol-1 Min-1
Uncatalyzed(Absent)	2.10	—-		3.99	—-
1.0 × 10-4	2.32	2.20		4.41	4.20
2.0 × 10-4	2.58	2.40		4.81	4.10
3.0 × 10-4	2.86	2.53		5.30	4.36
4.0 × 10-4	3.04	2.35		5.70	4.27
5.0 × 10-4	3.29	2.38		6.15	4.32
6.0 × 10-4	3.59	2.48		6.50	4.18

Change  in Temperature on reaction

The reaction was studied at different temperature i.e. 303, 308, 313 and 318K at the constant concentration of all the reactants. The result has been presented in the table 5.

Table 5: Effect of Temperature variation

[n-butyric acid] = 0.10 mole lit-1 [H2SO4] = 4.0 mole lit-1			[KMnO4] = 1.0 × 10-3 mole lit-1 Temperature = 308 K
Temperature (K)	Velocity constant for Uncatalyzed         NaLS = Nil			Velocity constant for Catalyzed NaLS = 1.0× 10-4 mole lit-1
	×10-3 Min-1	×10-3 Min-1		×10-3 Min-1	×10-3 Min-1
303	1.38	2.10		1.84	2.44
308	2.10	3.99		2.32	4.41
313	3.10	4.50		3.83	5.07
318	4.61	8.44		4.72	8.80
Selected Temperature (K)	Temp. coeff. for Uncatalyzed			Temp. coeff. for Catalyzed
	I step	II step		I step	II step
303-313	2.24	2.14		2.08	2.07
308-318	2.19	2.11		2.03	1.99

Different activation parameters like  ∆E^≠, ∆H^≠, ∆S^≠, pZ and  ∆G^≠ have been evaluated from the temperature variation studies, the various kinetic by their standard equations and reported in the table 6. The values of ∆E^≠ has also been calculate from the Arrehenius plots³¹ and have been reported in the respective table.

Table 6 : Thermodynamic and Activation Parameters (For Uncatalyzed and Catalyzed reaction)

[n-butyric acid] = 0.10 mole lit-1 [H2SO4] = 4.0 mole lit-1 Temperature = 308K				[KMnO4] = 1.0 × 10-3 mole lit-1 [NaLS]= 1.0 × 10-4 mole lit-1
Kinetic Parameters
Stages	∆E≠   KJ mol-1		∆H≠       KJ mol-1		∆S≠       Jmol-1K-1	Frequency factor pZ        dm3mol-1 Sec-1	∆G≠      KJ mol-1
	Cal.	Gra.
Uncatalyzed I stage (Without NaLS )	63.822	64.561	62.000		-86.83	7.78 × 108	35.254
Uncatalyzed  II stage (Without NaLS )	60.102	62.301	59.741		-88.83	6.10 × 108	32.378
Catalyzed    I stage (WithNaLS)	57.811	55.401	52.840		– 115.75	24.05 × 106	17.189
Catalyzed II stage (With NaLS)	57.673	58.357	55.797		– 100.80	14.52× 107	24.747

It was determined by analytical method. This involves the known excess of KMnO₄ over the substrate i.e. n-butyric acid kept at room temperature for a sufficiently long time (36 hours). The unreacted permanganate was estimated iodometrically. It has been found that the five mole of substrate consumes one mole of potassium permanganate. The catalyzed reaction is suggested to be proceeds as follows:

Propyl alcohal was identified by spot test method as given by Figel³² and Carbon dioxide have been determined by routine test as the end products. The formation of intermediate free radical is confirmed by induced reduction of mercuric chloride. Low value of energy of activation also supports the same.

Mechanism

On the basis of the results of kinetic measurements facts and discussion the following steps for the oxidation reaction of n-butyric acid in the absence and presence of sodium lauryl sulphate as catalyst has been suggested.

Mechanism and rate law for uncatalyzed oxidation

The mechanism proceeds with the formation of molecular HMnO₄ in sulphuric acid medium

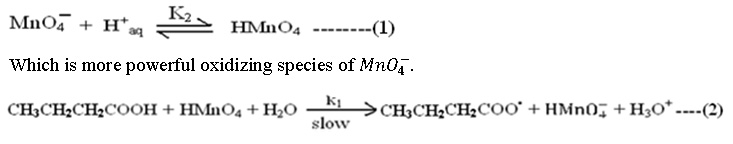
Step (2) is rate determining step. The cause of slowness is the involvement of three body collision which is difficult one. All subsequent steps are very fast and not of kinetic importance, are as follows;

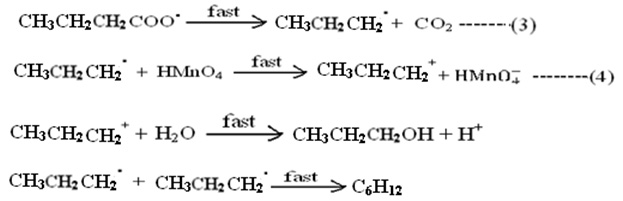
The above mechanism leads to suggest the rate expression for uncatalyzed reaction; in which the concentration of hydrogen ion and water have been withdrawn from main equation.

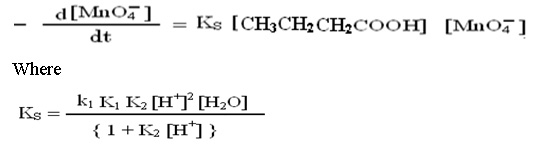
Mechanism and rate law for catalyzed reaction

The reaction rates have been found substantially increased in presence of anionic sodium lauryl sulphate surfactant. It is assumed that due to the electrostatic interaction between n-butyric acid and micelles of surfactant leads the increase in effective concentration which is responsible for the increase in reaction rate. The very low values of number ‘n’ of surfactant molecules i.e. below 20 are expected in micelles. The mechanism proposed, therefore involve the substrate – surfactant interaction, with the premiceller catalysis phenomenon as the n, calculated has the value below 20.

The following rate law expression may be derived from above discussed steps considering that catalyzed and uncatalyzed reactions proceeds simultaneously.

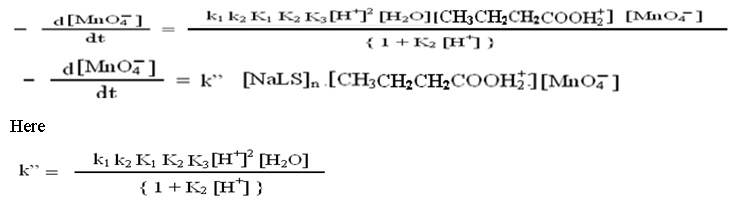
Discussion

In the studied reaction the order for n-butyric acid and molecular permanganate has been found as one i.e. HMnO₄ were found one in each case.The role of surfactant is only as premiceller physical catalyst with no covalent bond formation between surfactant – substrate association. Rate law involve the acid concentration term and water molecule. Zucker-Hammett, Bunnett’s and Bunnett-Olsen Hypotheses suggest the involvement of water molecule as a proton abstracting agent in the reaction.

Acknowledgement

The author Vandana Sharma is thankful to Dr. Smt. R. Vyas Head Deptt. of Chemistry Holkar Science College Indore for providing all necessary research facilities.

References

1. Bhagwat,V. W.; Pipada, M.;Tumalagada, S. B.; Pare, B. Ind. J. Chem., 2003, 42A, 1644.
2. Kabir-ud-din; Shakeel Iqubal, S. M.; Khan, Z. Ind. J. Chem., 2005, 42A,2455.
3. Prakash, R. J. Ultra Chem., 2010, 6(3), 357.
4. Bende, N.; Chourey, V. R. Res. J. Chem. Environ., 2013, 17(06), 75-87.
5. Sharma, V.; Chourey, V. R. J. Ultra Chem., 2013, 09(03), 287-302.
6. Sharma, V.; Chourey, V. R. Int. J. Advance Research, 2014, 2(3), 764-772.
7. Sharma, V.; Chourey, V. R. Int. J. Advance Research, 2014, 2(6), 617-625.
8. Vanangnudi, C.; Subbaiyan, M.; Srinivans, S. Asian J. Chem., 2007, 19(04), 71.
9. Hall, L.; Singh, A. C. J. Chem. Educ. 1988, 65,142.
   CrossRef
10. Sharma, A.; Sharma, A. K.; Gupta, K. S. J. Indian Chem. Soc., 2009, 86, 649.
11. Wiberg, K. B.; Steward, R. J. Am. Chem. Soc., 1956, 78, 1214.
    CrossRef
12. Bhale, V. M.; Mohammad, S.; Bhagwat, W. V.; Bafna, S. C. J. Sci. Ind. Research (India), 1953, 1954,12,13,521, Chem. Abst., 48,5620.
13. Khandual, N. C.; Satpathy, K. K.; Nayak, P. L. Indian J. Chem., 1973,11, 770-772.
14. Venkatraman R.; Rao S. B.  Indian J. Chem., 1972, 10, 165-167.
15. Khan Z.; Kabiruddin  Indian J. Chem., 2000, 39(A), 552.
16. Wankhade, C. B.; Khodakar, S. N.; Patel, N. T. Asian J. Chem., 2006, 18(4), 2538.
17. Vogel, A. I. “A text book of quantitative Inorganic analysis” Longman Green, London, 1964, 282.
18. Mehrotra, R. N. J. Chem. Soc., 1968, 1123.
19. Sankhla, P. S.; Mehrotra, R. N. Indian J. Chem., 1972,10,1081, 2077.
20. Zucker, L.; Hammett, L. P. J. Am. Chem. Soc., 1939, 61, 2791.
    CrossRef
21. Bunnett, J. F. J. Am. Chem. Soc., 1961, 83, 4968.
    CrossRef
22. Bunnett, J. F.; Olsen, F. P. Can. J. Chem., 1899, 1917, 1966, 44.
23. Paul, M. A.; Long, F. A. Chem. Rev., 1957,57,1.
    CrossRef
24. Bruice, J. C.; Katzhendler, J.; Fedar, L. J. Am. Chem. Soc., 1968, 90,133.
25. Sarasan, G. Asian J. Chem., 2003, 15(1), 133.
26. Prakash, R.; Agrawal, S. J. Ultra Chem., 2012, 8(3), 309.
27. Piszkiewicz, D. J. Am. Chem. Soc., 1977, 99, 1550.
    CrossRef
28. Raghavan. Ind. J. Chem., 1980, 19(A), 322-324.
29. Behara, G. B.; Mishra, S. S.; Samantaray  Ind. J. Chem., 1982, 21(A),1063-1065.
30. Pare, B.; Kaur, P.; Bhagwat, V. W.; fogliani, C. J. Korean Chem. Soc., 2004, 48,195.
    CrossRef
31. Laidler, K. J. “Chemical Kinetics”, Third Edn. Tata Mc. Graw Hill, Bombay, 2004, 39.
32. Fiegl, F. “spot test in Organic Analysis”, 1955, 174.