Correlation Between Parameters Related to Intramolecular Hydrogen Bond Strength and Hammett Constant in Para Substituted Benzoylacetone: A Theoretical and Experimental Study

Introduction

The concept of hydrogen bond, for the first time, had been proposed by Huggins in 1919 ¹. After that, many theoretical and experimental works have been done to study the properties of intramolecular and intermolecular hydrogen bond ^2-6. In an intramolecular hydrogen bond (IHB) system, both proton donor and proton acceptor groups are located in the same molecule. The cis-enol forms of β-diketones are engaged in an intramolecular hydrogen bond system and could be stabilized by a six membered chelated ring ^7-9. Formation of this kind of hydrogen bond causes an obvious affinity for bond equalization of the valence bonds in the resulting chelated ring. Thus, any parameter that affects the electron density of the chelating ring will change the hydrogen bond strength.

Two stable cis-enol forms of 1-Phenyl-1,3-butanedione, known as benzoylacetone (BA), as an asymmetric β-diketones, characterized by the position of the phenyl group, which can be attached at C2 or at C4(i.e. adjacent to C-O bond), Fig.1. They are labeled as BA-2 and BA-4, respectively.

By replacing the hydrogen atom in the para position of phenyl ring with the electron-withdrawing groups (EWG) or electron donating groups (EDG), the π-electrons in the chelated ring are significantly distorted. So the intramolecular hydrogen bond strength (IHBs) of these molecules are affected by varying in the bond lengths of chelated ring. The EWG tend to reduce IHB strength by two manners, the first conjugation with the enol double bond and the second by increasing positive charges on the carbonyl oxygen atom ^10-12.

As you know, Hammett quantified the effect of substituents on any reaction by defining an empirical electronic substituent parameter (σ), which is derived from the acidity constants, K_a’s of substituted benzoic acids ^13-14. The Hammett equation relates observed changes in equilibrium, rate constants, and physical properties with variations in structure to manage the systematic changes in the electron donating/withdrawing ability of substitutions. The aim of the present paper is to predict the structure, the conformational stabilities, and IHB strength of BA and its different para substitutions, X-BA, by means of density functional theory (DFT), Atoms-In-Molecules (AIM) ¹⁵, and Natural Bond Orbital (NBO) calculations. Afterwards the results related to IHB strength have been compared with the experimental enolic proton chemical shifts. These results, for the first time, to the best of our knowledge, were correlated with Hammett’s para function, σ_p, to point out a correlations between IHB strength and the parameters related to that with the electronic substitution effects on structure of titled molecules. So the substituent effect is discussed quantitatively by applying the Hammett equation.

Computational Methods

All the calculations on BA and X-BA molecules were performed by the use of Gaussian 09 of program ¹⁶.

The cis-enol structure of all molecules have been optimized at the B3LYP ^17-18, the second-order Møller-Plesset (MP2) ^19-20, and TPSSh ²¹ levels, using different basis sets, to confirm the relative stability of the cis-enol forms of titled molecules. The zero point vibrational energy, ZPE, corrections were obtained at the B3LYP level, without applying any scaling. The vibrational frequencies of the cis-enol forms were calculated at the B3LYP level of theory.

The SCRF–PCM method ²² were selected for studying the tautomerism in acetonitrile, carbon tetrachloride, and ethanol solutions at the B3LYP/6-311++G** level, according to which the solute is embedded in the dielectric medium surrounded by a cavity shaped in the form of the solute ^23-24. The van der Waals radii suggested by Bondi ²⁵ were adopted for atoms.

The AIM computations, such as the electronic charge density (ρ), its Laplacian (∇²ρ(r)), and the IHB energy (E_HB) were carried out by using the AIM2000 program ^26-27. The second-order interaction energies (E²), and natural charge of the bridged atoms (O, H, and O), were calculated using NBO 5.0 program ²⁸. For prediction of ¹HNMR chemical shift of the enolic proton, NMR calculations were applied using gauge independent atomic orbital (GIAO) method ^29-30 at the B3LYP/6-311++G** level of theory. The predicted ¹H chemical shifts are derived from δ =σ_o− σ. In this equation, δ is the chemical shift, σ is the absolute shielding of bridged hydrogen, and σ_o is the absolute shielding of hydrogen nuclei in TMS (Tetramethylsilane) as reference. Finally, correlations between some calculated and experimental IHBS parameters with σ_p Hammett equation have also been considered. Graphs were drawn and regression analyses were performed using Microsoft Office Excel, 2016 software.

Results and discussion

Tautomerism and IHB Strength

Cis-enol forms of β-dicarbonyl compounds stabilized by an intramolecular hydrogen bond. Two different cis-enol forms are noticeable in the BA and its para substituted, X-BA, as a case of unsymmetrical β-dicarbonyl compounds, (see Fig. 1).

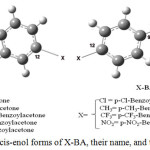Figure 1: Two stable cis-enol forms of X-BA, their name, and their numbering. Click here to View figure

 

The name and atom numbering of the stable forms are shown in Fig.1. For comparison, the relative stabilities of stable cis-enol forms of BA(BA-2 and BA-4) and its substitutions (X-BA-2and X-BA-4), along with the reported experimental and theoretical equilibrium constants (K_eq), and their dipole moments, calculated at different levels and basis sets of theory in gas phase and solutions, are listed in Table 1. Acetonitrile, ethanol, and carbon tetrachloride, as Polar and non-polar solvent, was selected for studying the enol-enol tautomerism in solution. According to Table 1, the energy differences between the mentioned stable cis-enol forms, are negligible (0.35-1.1, 0.55-0.76, 0.43-0.60, and 0.44-0.61 kcal/mol ranges in the gas phase, CCl₄, CH₃CN, and C₂H₅OH solvents, respectively). Upon ZPE corrections, these energy differences reduce to 0.28–0.59, 0.21-0.44, 0.19-0.33, and 0.15-0.34 kcal/mol, respectively. Therefore, coexisting of two stable cis-enol forms of X-BA in the sample is possible, which is in agreement with the experimental equilibrium constants. Also this Table shows no significant variation between experimental and theoretical equilibrium constants, K_eq. We calculated the equilibrium constants from ∆G^°= -RTln(K_eq) (1) equation, that ∆G^°₂₉₈=(G^°_X-BA-2– G^°_X-BA-4) (2) in 298K,. The Gibbs free energy values under standard conditions (G^°), which were calculated at B3LYP/6-311++G** within the harmonic approximation, were used for the evaluation of the X-BA-2«X-BA-4 equilibrium in the case of p-substituted benzoylacetone.

Table 1: Calculated relative energies in gas phase and solution (in kcal/mol), dipole moments, and theoretical and experimental equilibrium constants of X-BA-2 and X-BA-4 at different levels of theory.^a

	BA		Cl-BA			F-BA				CH3-BA			OCH3-BA		NH2-BA		NO2-BA		CF3-BA		OH-BA
	2	4	2	4	2		4		2		4		2	4	2	4	2	4	2	4	2	4
A/6-311++G**	0.0	0.60(0.29)	0.0	0.78(0.50)	0.0		0.83(0.49)		0.0		0.59(0.31)		0.0	0.64(0.28)	0.0	0.63(0.29)	0.0	0.69(0.37)	0.0	0.72(0.39)	0.0	0.76(0.37)
A /6-311G**	0.0	0.72(0.40)	0.0	0.90(0.54)	0.0		0.95(0.59)		0.0		0.72(0.39)		0.0	0.76(0.36)	0.0	0.74(0.37)	0.0	0.79(0.43)	0.0	0.82(0.45)	0.0	0.86(0.44)
A /6-31G**	0.0	0.65(0.33)	0.0	0.81(0.47)	0.0		0.85(0.50)		0.0		0.64(0.31)		0.0	0.69(0.28)	0.0	0.66(0.28)	0.0	0.71(0.36)	0.0	0.73(0.38)	0.0	0.77(0.34)
B /6-31G**	0.0	0.50	0.0	0.56	0.0		0.62		0.0		0.53		0.0	1.1	0.0	0.71	0.0	0.64	0.0	0.46	0.0	0.35
C /6-311++G**	0.0	0.56	0.0	0.75	0.0		0.78		0.0		0.54		0.0	0.57	0.0	0.77	0.0	0.77	0.0	0.73	0.0	0.67
CCL4 b	0.0	0.55(0.29)	0.0	0.71(0.44)	0.0		0.76(0.44)		0.0		0.54(0.25)		0.0	0.57(0.21)	0.0	0.53(0.21)	0.0	0.60(0.30)	0.0	0.65(0.34)	0.0	0.65(0.39)
CH3CN b	0.0	0.50(0.21)	0.0	0.59(0.32)	0.0		0.66(0.33)		0.0		0.50(0.19)		0.0	0.50(0.20)	0.0	0.44(0.15)	0.0	0.43(0.20)	0.0	0.53(0.24)	0.0	0.55(0.30)
C2H5OH b	0.0	0.50(0.22)	0.0	0.60(0.33)	0.0		0.66(0.34)		0.0		0.51(0.19)		0.0	0.50(0.19)	0.0	0.44(0.15)	0.0	0.44(0.20)	0.0	0.54(0.24)	0.0	0.56(0.31)
μ c	3.26	3.57	2.95	2.66		2.93		2.67		3.61		4.13	3.13	4.04	4.97	5.78	5.16	4.25	3.65	2.87	2.43	3.23
Keq (exp.) d	1.06(0.89)		1.00(0.93)			1.06(1.07)				1.05(0.96)			1.06(1.39)		1.06 (-)		1.06(-)		1.07(-)		1.1(-)

 

^aA, B, and C are calculated relative energies in gas phase at B3LYP, MP2,  and TPSSh levels, respectively, the values of ZPE are in parentheses.

^bCalculated  relative energies in various solvents at  B3LYP/6-311++G** level of theory.

^cCalculated dipole moment (Debye) in gas phase at B3LYP/6-311++G** level of theory.

^dCalculated equilibrium constants in gas phase  at B3LYP/6-311++G** level of theory and experimental equilibrium constants in parentheses from Ref. [43].

The parameters relate to intramolecular hydrogen bonding (IHB) strength, include optimized geometrical parameters, topological parameters, the natural bond orbital analysis (NBO), theoretical and experimental spectroscopic data consist of IR frequencies, NMR chemical shifts, for each stable form and their averages are collected in Table 2.

According to Table 2, the O…O distance in 4 form of X-BA is shorter than that in 2 form, therefore the IHB strength in X-BA-4 is stronger than that in X-BA-2. This results is agreement to the other parameters relate to intramolecular hydrogen bonding (IHB) strength in this Table. The afore mentioned result for IHB strength of X-BA-2 and X-BA-4, and comparing the geometrical parameters of chelated ring suggests that in the 4 form, X-BA-4, that the phenyl group and hydroxyl group are adjacent, therefore a conjugation between C=C and C-C and phenyl group is expected, in while in the 2 form, X-BA-2, there is a conjugation between ph and C=O, as reported by S.F. Tayyari et al. and R. Afzali et al. ³¹.

As Table 2 shows, some substitutions with electron donating effect make the IHB stronger, such as NH₂, OCH₃, OH, and CH₃ substitutions, while the electron withdrawing substitutions such as CF₃, and NO₂ decrease the IHB strength of titled molecules, in comparison with BA, as the parent molecule. However the substitutions like F and Cl have no important effect on the IHB strength. So the following trends in IHB strength of X-BA molecules are concluded:

CF₃-BA < NO₂-BA < Cl-BA ~ F-BA ~ BA < CH₃-BA < OCH₃-BA ~ OH-BA < NH₂-BA      (1)

Table 2: The calculated, experimental spectroscopic, geometrical, topological parameters, natural bond orbital analysis related to the IHB strength, and hydrogen bond energies of X-BA-2, X-BA-4 and its averaged.^a

	BA			Cl-BA			F-BA			CH3-BA			OCH3-BA
	2	4	Avg.	2	4	Avg.	2	4	Avg.	2	4	Avg.	2	4	Avg.
δ OH b	16.50	16.71	16.60(16.5)	16.52	16.74	16.63(16.41)	16.42	16.81	16.62(16.48)	16.6	16.95	16.78(16.6)	16.6	17.23	16.92(16.7)
υ OH b	3010	2939	2975	3022	2934	2978	3021	2920	2971	3002	2911	2957	2991	2874	2933
g OH b	938	990	987	971	983	977	980	994	987	978	989	984	978	986	982
R O…O c	2.522	2.515	2.518	2.522	2.513	2.517	2.523	2.511	2.517	2.520	2.510	2.515	2.518	2.503	2.511
R O-H c	1.006	1.009	1.008	1.001	1.010	1.005	1.006	1.011	1.008	1.007	1.011	1.009	1.007	1.013	1.010
<OHO c	148.9	150.4	149.7	148.7	150.3	149.5	148.8	150.4	149.6	149.0	150.7	149.9	149.2	151.2	150.2
EHBd	19.9	21.1	20.5	19.8	21.2	20.5	19.7	21.5	20.6	20.1	21.7	20.9	20.4	22.5	21.4
ρBCP	0.061	0.064	0.063	0.061	0.064	0.063	0.061	0.065	0.063	0.062	0.066	0.064	0.062	0.067	0.065
Ñ2ρBCP	-0.1514	-0.1517	-0.1516	-0.1515	-0.1518	-0.1517	-0.1513	-0.152	-0.1517	-0.1518	-0.1524	-0.1521	-0.1522	-0.1532	-0.1527
Lp(1)O→σ*O-H	4.24	3.91	–	4.26	3.97	–	4.23	4.03	–	4.3	4.07	–	4.36	4.2	–
Lp(2)O→σ*O-H	30.18	33.14	–	29.67	33.34	–	29.7	33.9	–	30.61	34.36	–	31.15	36	–
ΣLp(1,2)O→σ*O-H	34.42	37.05	–	33.93	37.31	–	33.93	37.93	–	34.91	38.43	–	35.51	40.2	–
∆E(HOMO – LUMO) e	4.67	4.42	4.55	4.57	4.32	4.45	4.67	4.42	4.54	4.64	4.35	4.50	4.49	4.21	4.35

Table 2: continue

	NH2-BA			NO2-BA			CF3-BA			OH-BA
	2	4	Avg.	2	4	Avg.	2	4	Avg.	2	4	Avg.
δ OH b	16.62	17.25	16.94(-)	16.30	16.22	16.26(15.67)	16.42	16.36	16.39(-)	16.54	17.27	16.91(-)
υ  OH b	2980	2863	2922	3048	3000	3024	3040	2989	3015	3000	2868	2934
g OH b	981	991	986	976	975	976	974	975	975	976	987	982
R O…O c	2.516	2.502	2.509	2.529	2.524	2.527	2.527	2.523	2.525	2.519	2.502	2.510
R O-H c	1.008	1.013	1.011	1.004	1.006	1.005	1.005	1.007	1.006	1.007	1.013	1.010
<OHO c	149.4	151.4	150.4	148.4	149.4	148.9	148.5	149.6	149.1	149.1	151.1	150.1
EHB d	20.6	22.7	21.6	20.0	19.8	19.9	19.3	20.1	19.7	20.2	22.6	21.4
ρ BCP	0.063	0.068	0.066	0.062	0.061	0.062	0.060	0.062	0.061	0.062	0.068	0.065
Ñ2ρBCP	-0.1523	-0.1532	-0.1528	-0.1499	-0.1499	-0.1499	-0.1505	-0.1503	-0.1504	-0.1520	-0.1532	-0.1526
Lp(1)O→σ*O-H	4.37	4.21	–	4.09	3.74	–	4.16	3.76	–	4.34	4.22	–
Lp(2)O→σ*O-H	31.62	36.44	–	28.32	30.53	–	28.82	31.05	–	30.73	36.21	–
ΣLp(1,2)O→σ*O-H	35.99	40.65	–	32.41	34.27	–	32.98	34.81	–	35.07	40.43	–
∆E(HOM O – LUMO) e	4.26	4.03	4.15	3.98	3.85	3.92	4.53	4.38	4.46	4.56	4.25	4.41

 

^aAll calculated at the B3LYP/6-311++G**  level, except for spectroscopic and proton chemical shift data that are calculated at the B3LYP/6-311++G**   level of theory. The experimental values are in parentheses.

^bδ, proton chemical shift in ppm; υ and γ are stretching and out-of-plane bending modes frequencies, respectively, in cm ^-1.

^cR is bond length in Å, <  is the bond angle in degrees.

^dE_HB is the IHB energy in kcal/mol.

^eThe energy difference between HOMO and LUMO orbitals in eV.

The relationships between the calculated and experimental parameters related to the IHB strength and Hammett substituent constant, σ_p.

The Hammett equation, as a linear free energy relationship, correlates the effects of substitutions on many different chemical properties of phenyl family compounds. This equation is written in terms of equilibrium constants (log₁₀ K = ρσ- log₁₀ K_o) (3). The ρ is a reliable empirical scale for the sensitivity of the reaction to the electronic substituent effect. One of the most surprising is the strength of O…H-O hydrogen bond, as an example of intramolecular hydrogen bond. According to the best of our knowledge, for the first time, we correlated the calculated and experimental parameters related to the IHB strength with electrophilic substituent constants, σ_p, for some para substitutions of benzoylacetone(X-BA) and their cis-enol stable forms(X-BA-4 and X-BA-2), as a β-diketones with phenyl substitution. The mentioned correlations of X-BA-2, X-BA-4, and their average are shown in Figs 2-11. These Figures show a good linear correlations between the mentioned parameters with σ_p, as: Parameter = ρσ_p+const. (4)

Except for log K_eq, the reported experimental and theoretical equilibrium constants between two stable cis-enol forms of X-BA, see Fig 2.

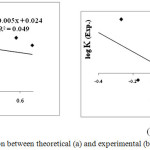Figure 2: The correlation between theoretical (a) and experimental (b) log Keq and σp. Click here to View figure

 

Correlation Between the Chemical shifts of Enolic Proton with σ_p

The experimental and theoretical proton chemical shifts of enolated proton (δOH), have important roles in characterization of the nature of IHB strength ³². The theoretical and experimental δOH of X-BA-4 and X-BA-2 forms and their averaged values are given in Table2. According to this Table, the IHB strength of the mentioned molecules (trend 1) are in agreement with the increasing of δOH, experimentally and theoretically.

The Fig 3a-b show linear correlations between the theoretical and experimental δOH of X-BA-4 and X-BA-2 forms and their averaged and σ_p, i.e. δ=ρσ_p+constant (5). The linear dependence with high regression coefficients (R²=0.795, 0.923, 0.933, and 0.980 for X-BA-2, X-BA-4, their averaged, and experimental chemical shifts, respectively) indicates that there is strong correlation between IHB energies with δOH values as a descriptor of IHB nature strength. The chemical shifts of enolic protons were observed at about15.8-17.3 ppm, its signal shifted to the upper magnetic field with increasing of the IHBs. These correlations supports the conjugation effect between the p-substituted aromatic system and the enol chelated ring.

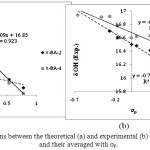Figure 3: The linear correlations between the theoretical (a) and experimental (b) δOH of X-BA-2, X-BA-4 forms, and their averaged with σp. Click here to View figure

 

Correlation Between the Positions of IR Bands Related to IHB_S with σ_p

The experimental and theoretical infrared spectroscopy bands, include theOH stretching (nOH) and out of plane bending of OH (gOH) have important roles in characterization of the nature of IHB strength ^32-34. The IHB strength of the mentioned molecules are in agreement with the increasing of gOH and decreasing of nOH positions, experimentally and theoretically. The mentioned results of X-BA-4 and X-BA-2 forms and their averaged values are given in Table2. In addition the position of broad IR band at about 1600cm^-1 for the enol forms, as was reported by  H.I. mai, and T. Shiraiwa et. al.³⁵ and attributed to the nC=O (which is coupled to nC=C, δOH, δCH_α, according to ³¹, also can be used for IHB strength ^36-37. A red shift of this band could be attributed to decreasing of IHBs.

The Fig. 4a-b show linear correlations between the theoretical νOH and γOH frequencies of X-BA-4 and X-BA-2 and their averaged and σ_p, according to equation (4). The linear dependence with regression coefficients (see Fig.4) indicates that there is strong correlation between IHB energies with ^νOH, as a descriptor of IHB nature strength. According to Fig.4b, there is no good correlation between ^γOH values and σ_p, this behavior could be easily explained if we consider the calculation results. The calculation results show that there are coupling between γOH with out of plane bending of CH_α and the hydrogen belong to the phenyl ring.

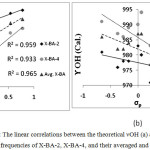Figure 4: The linear correlations between the theoretical νOH (a) and γOH (b) frequencies of X-BA-2, X-BA-4, and their averaged and σp. Click here to View figure

 

The Fig. 5 shows a good linear correlation between the experimental frequency of broad band at about 1600cm^-1 of the mentioned molecules and σ_p. The linear dependence with high regression coefficients (R²=0.991, and 0.962 for EWG and EDG, respectively) indicates that there is strong correlation between IHB energies with the above experimental values as a descriptor of IHB nature strength. The Fig.5 shows a positive slope in the region of the positive σ_p, while, with a negative slope in the region of the negative σ_p. Furthermore, as it is expected this frequency shift could be a criterion for the IHB strength. Therefore the EDG to EWG may have great effect on the hydrogen bonding.

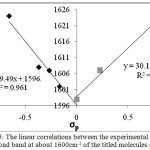Figure 5: The linear correlations between the experimental frequency of broad band at about 1600cm-1 of the titled molecules and σp. Click here to View figure

 

Correlation Between σ_p and Geometrical Parameters Related to IHB_S

Geometrical parameters have various applications in the explanation of IHB strength in the cis-enol forms of β-diketones ^{33-34, 38}. The IHBs depends on the nature of the β and α substitutions ^33-34.We considered the O…O and O…H distances, the O-H and O-H+O…H bond lengths, and the O…H-O angle parameters in the titled molecules, calculated at B3LYP/6-311++G**.  These bond length changes are attributed to changes in the π-electron delocalization of the chelated ring. The mentioned geometrical parameters correlated as good linear versus σ_p with a correlation coefficients near to onefor X-BA-2 and X-BA-4 and their averaged (see Fig.6a-e). This result could be attributed to the effect of electron-withdrawing and electron donating substitutions on the hydrogen bond strength in aromatic system and its relation with Hammett equation. According to Table 2, by increasing the hydrogen bond strength, the calculated O…H and the O…O bond lengths decreases, while the calculated OHO bond angle and the O-H bond length increase.

Figure 6a.e: The linear correlations between σp and the geometrical parameters related to IHB strength. Click here to View figure

 

Correlation Between σ_p and AIM Results Related to IHBs

In the topological theory of AIM, when two neighboring atoms are chemically bonded, a bond critical point (BCP) appears between them and the nature of chemical bonds are described by total electronic density, ρ(r), and its corresponding Laplacian, ∇²ρ(r). One of the most useful of theoretical methods to estimate hydrogen bond energy, has been explained by Espinosa et al. ³⁹. Who found that IHB energy may be correlated with the potential electron energy density at critical point, by the expression   E_HB= 1/2 × V(BCP)  (5). The hydrogen bonding energies (E_HB), according to Espinosa et al. suggestion, the calculated total electronic density and its corresponding Laplacian for all O…H bonds of stable cis-enol forms and their averaged, calculated at B3LYP/6-311++G** level, are given in Table 2. According to this table, the IHBs of titled molecules are in agreement with trend (1).

The Fig. 7a-c show good linear correlations between the E_HB, ρ(r), and its corresponding Laplacian, ∇²ρ(r), at O…H bond critical point of X-BA-4 and X-BA-2 forms, and their averaged and σ_p with a correlation coefficients near to one. It means that the topological parameters as well as the mentioned parameters described the relationship between the H-bond strength and σ_p.

Figure 7: Hammett plot for AIM results related to IHBs, IHB energies (kcal/mol) (a graph), electron density at bond critical points (b graph), and the Ñ2 ρBCP (c graph). Click here to View figure

 

Correlation Between σ_p and NBO Results Related to IHBs

The NBO study, such as charge analysis, Wiberg bond orders, and hyperconjugative interactions, can be used as the other method for characterization of IHBs. In Weinhold’s NBO calculation, hyperconjugation has a stabilizing effect that arises from delocalization of electron density from filled Lewis type NBO (bonding or lone pair) to another neighboring electron deficient orbitals, non-Lewis type NBO, (such as antibonding or Rydberg), when these orbitals are properly oriented. For each donor NBO (i) and acceptor NBO (j), stabilization energy can be described by means of second-order perturbation interaction energy (E⁽²⁾) ⁴⁰.

One of the important hyperconjugative interactions that is proportional to hydrogen bond strength, is Lp(O)→σ*(O–H), which are shown in the Table 2. The Fig. 8a-c correlated the mentioned correlation with σ_p for X-BA-2 and X-BA-4 and their averaged of the titled molecules, which indicates excellent agreement between the above E⁽²⁾ and σ_p. For LP(1)O → σ*O-H, R²=0.920, 0.884, and 0.911, for X-BA-2, X-BA-4, and their averaged, respectively. The correlation coefficients for LP(2)O →σ*O-Hare 0.964, 0.931, and 0.961, for X-BA-2, X-BA-4, and their averaged, respectively. Additionally we considered the mentioned correlation for ∑LP(1),LP(2)O →σ*O-H with σ_p (R²=0.964, 0.928, and 0.959, for X-BA-2, X-BA-4, and their averaged, respectively).

Figure 8a.c: The linear correlations between second order perturbation energy (E(2)) as lp(O)→σ*(O–H) with σp. Click here to View figure

 

The calculated Wiberg bond orders ⁴¹ of O-H, O…H, and O…O bonds for X-BA-2, X-BA-4, and their averaged, for comparison, are collected in Table 3. We correlate the mentioned bond orders with the σ_p. The best linear relationship was between the O-H bond order and σ_p, (R²=0.959, 0.903, and 0.953, for X-BA-2, X-BA-4, and its averaged, respectively, see Fig. 9a-c).

Figure 9a.c: The linear correlations between bond orders of O-H (a), O…H (b), O…O (c) and σp. Click here to View figure

 

Table 3: The bond orders of O-H, O…H, and O…O of p-substituted benzoylacetone.

Bond prder	BA		Cl-BA		F-BA		CH3-BA		OCH3-BA		CF3-BA		NH2-BA		NO2-BA		OH-BA
	2	4	2	4	2	4	2	4	2	4	2	4	2	4	2	4	2	4
O-H	0.6137	0.6057	0.6149	0.6045	0.6149	0.6030	0.6128	0.6026	0.6116	0.5985	0.6067	0.5977	0.6105	0.5977	0.6178	0.6111	0.6126	0.5977
O…H	0.1231	0.1328	0.1110	0.1334	0.1111	0.1235	0.1139	0.1248	0.1154	0.1295	0.1086	0.1151	0.1168	0.1308	0.1070	0.1136	0.1142	0.1301
O…O	0.0567	0.0587	0.0564	0.0585	0.0561	0.0588	0.0565	0.0594	0.0559	0.0597	0.0571	0.0570	0.0551	0.0594	0.0574	0.0566	0.0557	0.0599

 

The natural charge on the bridged hydrogen, obtained by the NBO calculations for optimized geometries of X-BA-2, X-BA-4 enol forms and their averaged, are presented in Fig. 10. Good linear relationship between natural charge bridged hydrogen and σ_p, (R² =0.960, 0.974, and 0.969, for X-BA-2,   X-BA-4, and its averaged, respectively) implies that by increasing the acidic nature of bridged hydrogen (increasing in its positive natural charge), the IHB power increases.

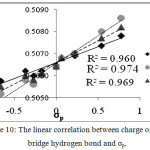Figure 10: The linear correlation between charge of H on bridge hydrogen bond and σp. Click here to View figure

 

Correlation Between σ_p and the Energy Difference Between the Orbitals of HOMO and LUMO

The HOMO characterizes the ability to donate an electron where LUMO represented the ability to obtain the electron, and the energy gap between the HOMO and LUMO characterizes the molecular chemical stability ⁴². The energy difference between the HOMO and LUMO are in the 3.85- 4.67 eV range (see Table 2), for the title compounds. This energy gap indicates that structure of the title molecules are very stable. Our results show that there are good linear correlations between σ_p and the energy difference between HOMO and LUMO in the studied molecules, see Fig.11. This figure shows a positive and negative slopes in the region of the negative and positive σ_p, respectively.  Therefore the EDG to EWG may have great effect on the energy difference between HOMO and LUMO orbitals.

Figure 11: Correlation between σp and the energy difference between the orbitals of HOMO and LUMO related to IHBs with σp. Click here to View figure

 

Conclusion

The intramolecular hydrogen bond for the BA and its substitutions in para position have been investigated using B3LYP/6-311++G** level of theory. The results obtained from DFT calculations, the topological parameters, geometrical parameters, NBO method, theoretical and experimental IR and NMR spectroscopy, have be used to estimate the IHB strength. All these methods show that an electron donating substitution at para position, such as NH₂, OMe, Me, and OH, increases the hydrogen bond strength, while electron withdrawing substitutions, such as NO₂ andCF₃decreases the IHB strength. The F and Cl substitutions have no significant effect on the IHB strength. According to various correlation graphs, correlation between σ_p and the above parameters for X-BA-4 and X-BA-2 forms, and their averaged show good linear dependence with high regression coefficients, but there is not good correlation between logK_eq and Hammett substituent constant.

Acknowledgment

This work was financially supported by the Ferdowsi University of Mashhad, Iran (grant No. 42453).

References

1. Huggins M. L., Ph.D Thesis, University of California, 1919.
2. Fuster F., and Grabowski S. J., J. Phys. Chem. A, 2011, 115, 10078- 10086.
   CrossRef
3. Lopes Jesus A. J., and Redinha J. S., J. Phys. Chem. A, 2011, 115, 14069-14077.
   CrossRef
4. Zahedi-Tabrizi M. and Farahati R., Comp. Theor. Chem., 2011, 977, 195-200.
   CrossRef
5. Bende A., Theor. Chem. Acc., 2010, 125, 253-268.
   CrossRef
6. Vakili M., Tayyari S. F., Kanaani A., Nekoei A. R., Salemi S., Miremad H., Berenji A. R. and Sammelson R. E.,  J. Mol. Struct., 2011, 998, 99-109.
   CrossRef
7. Vakili M., Nekoei A. R., Tayyari S. F., Kanaani A. and Sanati N.,  J. Mol. Struct., 2012, 1021, 102-111.
   CrossRef
8. Berenji A. R., Tayyari S. F., Rahimizadeh M., Eshghi H., Vakili M. and Shiri A., Spectrochim. Acta A, 2013, 102, 350-357.
   CrossRef
9. Gilli G. and Gilli P., The nature of hydrogen bond, Oxford: Oxford University Press, 2009.
   CrossRef
10. Tayyari S. F., Najafi A., Emamian S., Afzali R. and Wang Y. A., J. Mol. Struct., 2008, 878, 10-21.
    CrossRef
11. Zahedi-Tabrizi M., Tayyari F., Moosavi-Tekyeh Z., Jalali A., and Tayyari S. F., Spectrochim. Acta A, 2006, 65, 387-396.
    CrossRef
12. Tayyari S. F., Milani-Nejad F. and Rahemi H., Spectrochim. Acta A, 2002, 58, 1669-1679.
    CrossRef
13. Schwarzenbach R. P., Gschwend P. M., Imboden D. M., Environmental Organic Chemistry, 2^nd Ed., Wiley-Interscience Publishers, 2003, chapter 8, 253.
14. Jaffe H. H., A Re-examination of the Hammett equation, Chem. Rev., 1953, 53, 191-261.
    CrossRef
15. Bader R. W. F., Atoms in Molecules, A Quantum Theory, Oxford University Press, New York 1990.
16. Frisch et. al. M. J. Gaussian 09, Revision A.02-SMP, Gaussian, Inc., Wallingford CT, 2009.
17. Becke A. D., J. Chem. Phys., 1993, 98, 5648-5652.
    CrossRef
18. Lee C., Yang W., and Parr R.G., Phys. Rev. B, 1988, 37, 785-789.
    CrossRef
19. Muller C., and Plesset M. S., Phys. Rev., 1934, 46, 618–622.
    CrossRef
20. Frisch M. J., Head-Gordon M., and Pople J. A., Chem. Phys. Lett., 1990, 166, 275–280.
    CrossRef
21. Tao J. M., Perdew J. P., Staroverov V. N., Scuseria G. E., Phys. Rev. Lett., 2003, 91, 146401–146404.
    CrossRef
22. Tomasi J., and Persico M., Chem. Rev., 1994, 94, 2027-2094.
    CrossRef
23. Pascual-Ahuir J. L., Silla E., Tomasi J., and Bonaccorsi R., J. Comp. Chem., 1987, 8, 778-787.
    CrossRef
24. Mennucci B., and Tomasi J., J. Chem. Phys., 1997, 106, 5151-5160.
    CrossRef
25. Bondi A., J. Phys. Chem., 1964, 68, 441-451.
    CrossRef
26. Biegler-König F. and Schönbohm J., AIM2000 Version.2.0.
27. Bader R. F. W., Tang Y. H., Tal Y., and Biegler-König F. W. J., Am. Chem. Soc., 1982, 104, 946-952.
    CrossRef
28. Glendening E. D., Badenhoop J. K., Reed A. E., Carpenter J. E., Bohmann J. A., Morales C. M. and Weinhold F., Theor. Chem. Inst., University of Wisconsin, Madison, WI, 2001, (http://www.chem.wisc.edu/∼nbo5).
29. McWeeny R., Phys. Rev., 1962, 126, 1028-1035.
    CrossRef
30. London F., J. Phys., Radium, 1937, 8, 397-409.
    CrossRef
31. Afzali R., Vakili M., Tayyari S. F., Eshghi H., and Nekoei A. R., Spectrochim.Acta Part A: Mole and Biomol. Spect., 2014, 117, 284-298.
    CrossRef
32. Lopes A. J. and Redinha J. S., J. Phys. Chem. A, 2011, 115, 14069-14077.
    CrossRef
33. Afzali R., Vakili M., Nekoei A. R., and Tayyari S. F., J. Mol. Struct., 2014, 1076, 262-271.
    CrossRef
34. Vakili M., Tayyari S. F., Nekoei A. R., Miremad H., Salemi S., and Sammelson R. E., J. Mol. Struct., 2010, 970, 160-170.
    CrossRef
35. I.mai H.,  Shiraiwa T.,  Oiwa M., chem. soci.  Japan, 1977, 8, 1081-1086.
36. Perrin C.L., Ohta B.K., Bioorg. Chem., 2002, 3, 3-15.
    CrossRef
37. Perrin C.L., Ohta B.K., , J. Mol. Struct., 2003, 644, 1-12.
    CrossRef
38. Tayyari S. F., Emampour J. S., Vakili M., Nekoei A. R., Eshghi H., Salemi S., and Hassanpour M., J. Mol. Struct., 2006, 794, 204-214.
    CrossRef
39. Espinosa E., Molins E. and Lecomte C., Chem. Phys. Lett., 1998, 285, 170-173.
    CrossRef
40. Reed A. E., Curtiss L.A., Weinhold F., Chem. Rev., 1988, 88, 899-926.
    CrossRef
41. Wiberg K. W., Tetrahedron, 1968, 24, 1083-1096.
    CrossRef
42. Kosar B. and Albayrak C., Spectrochim. ActaA, 2011, 87, 160-167.
    CrossRef
43. Borisov E. V., Skorodumov E. V., Pachevskaya V. M. and Hansen P. E., MRC, 2005, 43, 992-998.
44. Kumutha R., Sampath krishnan S., and Thirumalai kumar M., Orient. J. Chem., 2014, 30(4), 1905-1912.
    CrossRef
45. Esmaeili B., Beyramabadi S. A., Sanavi-khoshnood R. and Morsalia A., Orient. J. Chem., 2015, 31(4), 2129-2135.
    CrossRef
46. Wala faris M. and Zaki safis S., Orient. J. Chem., 2014, 30(3), 1045-1054.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.