Thin Double Wall Boron Nitride Nanotube: Nano-Cylindrical Capacitor

Introduction

NSCCE or “Nanometer-scale capacitive charging effect” currently is familiar, e.g., the “coulomb blockade phenomenon” in the quantum dots^1,2 . However, they are arduous for resolving the detailed radial charges repartition within the nanostructures. Using SWBNNTs @ SWBNNTs double wall tubes; it has been discussed the “radial” charge distributions of multilayered molecular capacitors.

Designing and control of Nano-tubes diameters are requirement to develop Nano-tube growth method. Nano-tubes with the diameters of less than one nanometer provide the ideal Nano-spaces in X-dimension³. A few years ago, it has been suggested which the sizes of the catalysts used in the metal catalyze CVD (chemical vapor deposition) can explain the diameter of grown carbon nanotube⁴.This opinion has been confirmed by the seeing that a catalytic particle in the end of chemical vapor deposition grown nanotube has size proportional with the Nano-tubes diameters⁵.

Chin Li Cheung, illustrate clearly the concepts of different sizes nano cluster catalysts which they can be used for controlling the structures and diameters of “CVD” grown nanotubes⁶. Small-diameter carbon nanotubes indicate to many exotic properties such as an-isotropic optical absorption spectra⁷ and superconductivities emanate from a “Pearle” distortion^8,9. This finding has stimulated much fondness in studies of a small nanotube in both theoretically and experimentally^10-14 . BN-Nano-tubes (BNNTs), which firstly synthesized and predicted through Chopra work and Rubio respectively^15,16, has a unique structural syllogism to carbon Nano-tubes but, contrary to the C-N-T being semiconductor or metallic depending on their chirality¹⁶. BNNT is usually can be used as an insulator regardless of its diameter and helicity or the number of walls^15-17.

Experimental result has shown that a small SWNT is usually found inside a multi-walled CNT^11-13. Therefore, there are strong incentive for studding in details the stabilities and interaction of narrow BNNT inside a bigger one in viewpoint of diameter, which makes easier for understanding the experimental result. Furthermore, the studies of double-walled boron nitride Nano-tubes (DBNNTs) have displayed interesting variations in its electronic properties comparing with those of free-standing part of BNNTs¹⁸. So it is also significant for seeing the interaction energies associated and inter wall coupling behavior with the narrow BNNTs^17,18.

B-N nanotube possesses grate band gap around 6 eV regardless of diameters, chirality, electronic properties and the number of walls15, 19. Furthermore, they are stable in view-point of mechanical and chemical structures²⁰. Therefore, narrow single-wall BNNT can widely be applies as an ideal Nano-tube for the Nano sciences for producing suitable material such as; capacitor, atomic wire, and semiconductor^{21, 22.} In our study the SWBNNs are special material as an insulator for producing Nano-cylindrical capacitors²².

Ryo Nakanishi reported an important synthesis method of a narrow SWBNNT having uniform distribution of diameter around 0.7 0.1 nm¹. Their strategies to synthesize thin BNNTs are for combining the Nano-template reaction using Single wall carbon Nano-tubes which has developed in the past ten years²³. In their systems, precursor molecules including Ammonia Borane Complexes or ABC, including boron and nitrogen were en-capsulated first in the single wall carbon tubes followed by suitable thermal decomposition-fusion²² reaction inside the SWCNTs^22,23.

It has been used arc-grown SWCNTs²⁴ with distribution (diameter) around 1.4 nm²⁴ as a model for synthesizing narrow SWBNNT^22,24. Those distributions of SWCNT-models are essential for realizing the diameter selective synthesizing of BNNTs.

In this investigation, the systems have been simulated based on the various distribution diameters of SWBNNTs @SWBNNTs corresponding the experimental results of Ryo Nakanishi results¹ .So we have started for answering to some questions for the mechanism of  the radial charge distributions  on the inner and outer electrodes, band gapes, potential difference²³ between two layers of the Nano cylindrical²⁴ capacitor and the capacitance of our system when the inner tubes are semiconducting²⁵, and the others are metallic²⁶.

Gugang Chen in the studies of doped double-walled carbon nanotubes²⁶ exhibited the Resonant- Raman-Scattering (RRS) from the phonons²⁶ on each carbon shell determines the radial charges distributions²⁶. The self-consistent including tight-binding model (SCTB) confirms²⁵ the observed molecular faraday-cage effects, so most of the charges reside on the outer-walls, even when these walls were originally²⁶ semiconducting and the inner-walls were metallic^24-26.

Those systems have been modeled as three-layer cylindrical capacitor within bromine anion forming the shell (around the outer nanotubes²⁶). The total energies contain 3 terms including the inner tube, outer tube and band structures of the electrostatic energies “  for the three-layer charge distributions:

The signs “ i ” and “ k ” label the wave vector and occupied band for the outer  or inner tube²⁶.

They assumed that the surpluses charges on both shells are distributed in the infinitely thin-walls at the nuclear radiuses of those shell^{26, 27}. The resulting electrostatic energies of the triple-walled capacitors are:

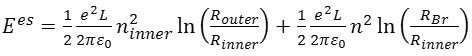
where(ε₀) is the permittivity of free space²⁷, L is the unit-cell length of the outer tubes and (n) is the linear densities of surpluses holes for the inner tubes.

There are two physical properties acts in concert²⁷ for isolating most of the holes into the outer nanotubes. (1): the gap band of the thinner diameter tubes towards the larger one, so they empty last²⁸. (2) The cylindrical-geometry rather raises the electrostatics potentials in the inner tubes²⁷. Lonely the charges on the inner tubes in the chirality of Zigzag (n, 0) of BNNTs are anticipated to have direct band gaps²⁷. On the other side the armchair (n, n) of BNNTs will have indirect band gaps²⁷.  Because of its large band gap around 5 eV, experiments²⁸ using BNNT as the conduction-channel²⁹ for field effect transistors²⁹ or FETs showed that BNNT allowed transport through only the valence band²⁸. The other important features about the band gaps of BNNTs are that they are tunable by doping with carbons²⁹, radial deformation³⁰, or by applying the transverses electric fields through the BNNTs so-called giant-stark-effect^31-33 .

Theoretical band structure calculation suggested that “SWBNNT” can either be n-type or p-type semiconductor by controlling the composition of carbon into “SWBNNTs”. Carbon impurities on a boron site result in electron carriers while on a nitrogen site result in hole carriers³⁴.

In this study it has been exhibited that the piezoelectricity³⁴ for SWBNNTs causes for increasing the capacities of SWBNNTs @ SWBNNTs capacitor comparing to SWCNTs @ SWCNTs. This phenomenon³⁵ originated from the deformation effects due to the tumbling of the planar hexagonal boron nitride network to produce tubular structures³⁵. It has been exhibited by Nakhmanson that BNNT could be excellent piezoelectric systems³⁶. As instant, piezoelectric constants for variant zigzags of SWBNNT were found for increasing along with the decreaseing of the radius in several BNNTs³⁶. Experimentally³⁷, Bai has exhabited that under in situ elastic bending deformation³⁶ or EBD at room temperature high-resolution-transmission-electron- microscope^36,37, a normally electrically insulating³⁷ MW BNNT may transform to a semiconductor³⁷.

K. Uchida et al^38-39 in a discussion of quantum effect in the cylindrical carbon nanotubes capacitor exhibited that the distributions of the accumulated charges in the inner tubes are quantum  mechanically³⁷ spilled outward, while that in the outer tubes are penetrating inwards³⁸. They have shown the reflecting those charges spills, the electrostatic capacitance of the systems are larger than what would be expected from the classical theories³⁸.

Finally, they have shown that the capacitance exhibit two principal quantum effects, (1): the capacitance shows a large bias dependence³⁸, reflecting the densities of states of the carbon Nano tube electrodes. (2): the capacitances are enhanced according to a quantum mechanical spill of the stored electrons density from the tubes walls of the CNTs^36-38.

Based on our previous works^40-61, we simulated our model in viewpoint of different band gap energies via considering the single wall boron nitrides as both inner and outer tubes with variant diameters and chirality in the ranges of (6.0 <d<8.0 ) and (11.0 <d< 16.0 ) for inner and outer tubes respectively.

Theoretical Background

Carbon nanotube is thin seamless graphitic cylinders³⁹, which exhibit an unusual combination of the Nano-meter size diameter and Milli-meter size length³⁹. These topologies, are included with the absence of defects³⁸ on the macroscopic scales⁶², yields to uncommon electronic properties of individual^62,63 SWCNTs that depends on their diameters and chirality⁶³, can be either⁶³ insulating, metallic or semiconducting^64,65.

Consider a cylindrical capacitor of length “d_i”, inner radius “R_inn”, outer radius “R_out”, and with charges Q =d_i.q_λ which q_λ is the charges per unit length (magnitude) on each cylinders (Scheme1). Assume “d_i”, >> “R_inn”, or “R_out”, and Neglect fringing and   electric fields between cylinders: use Gauss’ law

and electric potentials between cylinders: use

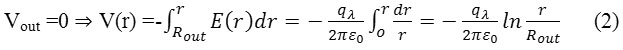
and

and capacitances for cylindrical geometries are:

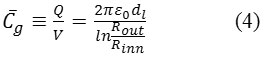
which “K” is the dielectric constant of the system⁶⁵.

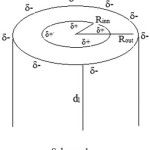Scheme 1  Click here to View scheme

 

is positive quantities because

is a positive quantities these because outer layers are at a higher potential than the inner layers. In our systems the calculation of the nano-cylindrical capacitors can be obtained from the electrical potential

ø(r,z)

in the spaces between two coaxial cylinders of radii R_inn and R_out and finite length d_i  in the z direction,

0 ≤ z ≤ di.

We supposed the geometrical capacitances in our systems are a function of di, R_inn R_out 

or

Cg = F(di,R_inn, R_out).

Bilalbegovi^66-68with a molecular dynamic simulation and extension series based on Bessel functions⁶⁹ has modified and discussed that capacitance around the shorter coaxial cylinders of radios⁶⁹. So the capacitance in our model can be calculated via

in the finite Nano-meter scales cylindrical-capacitor based on the classical electrodynamic⁸⁵. For calculation the capacitance for the eq.4 and eq.5 for

the potential difference applied between two cylindrical plates V=V_(inn)-V_(out) has been calculated by pop = chelpG commands⁷⁶.

Computational Details

Calculations were accomplished using GAMESS-US packages⁷². In this work, it has been mainly focused for optimization of each tube with DFT methods^73-77 consist of the m06 and m06-L⁷⁴. The m062x⁷⁴, m06-L⁷⁴, and m06-HF⁷⁴ are a unique Meta hybrid⁷⁴ DFT functional with a good correspondence in non-bonded⁷⁸ calculations and are useful for calculating the energies of the distances between two coaxial cylinders of radii  and  in the cylindrical capacitor⁷³.  The Perdew, Burkeand Ernzerhof (PBE)⁷⁵ exchange correlation⁷⁵ (XC) functional^74,75 of the generalized-gradient-approximations⁹⁵ (GGA) are adopted. The lattice constant has been optimized for the atomic coordinate and has done through the minimization of the total energies. For geometries optimizations, all the internal coordinates were relaxed until the Hellmann-Feynman-forces⁷⁴ was less than 0.005 angstrom.

At each inter tube configurations, a single point calculation is carried out and the total energies are recorded. The resulting sliding rotation energy surface is used for fixing our model in a better position.

We employed DFT theories with the van der Waals DFT for modeling the exchange-correlation energies of SBNNTs and SWCNs⁷⁶. The {ζ-basis set} with polarization⁷⁶ orbital was used for single wall tube⁷⁶.

For non-covalent approaches, DFT methods disable for describing van der Waals^{73,77 .} The other functional are correctly insufficient for showing the correlation and exchange energies in non-bonded medium-ranges distances. Furthermore, recent study has illustrated that the medium-range exchange^78,79 energies leads to the large systematic errors⁷⁸ in the prediction of molecular propertie⁷⁹.

We further calculated the interaction energies between two coaxial cylinders of radii “R_inn” and “R_out”

for SBNNTs and SWCNs in the structures. The dielectric permittivities as function of dielectric size were determined via Abinito calculation^78-79. The interaction energies for capacitor were calculated via an extendedhuckel method in all items according to the eq.6.

Where the “ΔE_s” is the stability energy of capacitor.

The charge transfer and electrostatic potential-derived also calculated using the “Merz-Kollman-Singh⁸⁰, Chelp⁸¹, ChelpG⁸² and MESP^83-84.

The MESPs are calculated and distributed at large number of grid points⁸⁴ in a cube regularly.

The representative⁸⁵ atomic charges⁸⁶ would be computed as averages values over a few molecular conformations for the molecules^86,87.

The electron densities Both  of & Laplacian⁸⁸ and Gradient norms⁸⁹, value of orbital wave function⁹⁰, electron spin densities⁸⁸, localization function (ELF)⁸⁹, localized orbital locator⁹⁰, electrostatic potential⁸⁸ from nuclear- atomic-charges, electron total electrostatic potential (ESP)⁹⁰, and the exchange-correlation density, correlation hole and correlation factor, Average local ionization energy using the Multifunctional-Wave-function Analyzer^88-90.

Result and Discussion

We first consider the h-BN sheet and 3D BN tubes in various diameters and chirality where the (5, 5) @ (8, 8) structure is found as a stable form compared to other forms.  The stability depends on the distance between inner radius “R_inn”, and outer radius “R_out in one hand and the chirality on other hand Table1. The minimum energies are calculated based on eq.9 in terms of the total energy of the optimized structures and are listed in Table1.

The differences in the band structure and Fermi⁸⁸ level energy of different tubes have been calculated. Furthermore, we have presented the number of states in unit energy interval through density of states (DOS) (Fig.1). DOS⁸⁸ was plotted as a curved map and we have considered those graphs as a tool for analyzing the nature of electronic structure in our systems^88,89. The original total DOS (TDOS)⁸⁹ of our system was calculated based on References {108-110}^108-110 in Figs. 2, 3, 4 and 5.

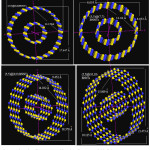Figure 1: Dimension of MWBNNTs with various diameters and chiralities  Click here to View figure

 

Figure 2: TDOS, PDOS, OPDOS versus energy for (5,5)@(8,8) BNNTs Click here to View figure

 

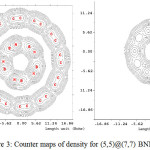Figure 3: Counter maps of density for (5,5)@(7,7) BNNTs Click here to View figure

 

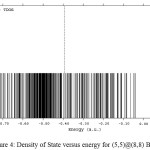Figure 4: Density of State versus energy for (5,5)@(8,8) BNNTs Click here to View figure

 

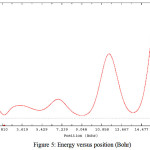Figure 5: Energy versus position (Bohr) Click here to View figure

 

The interaction energies for capacitors were calculated in all items according to the eq. 6

ΔEs(eV) = (Ec- {(2E_Dopant-G + E_h-Bn)} +E_BSSE

Where the “ΔE_S” is the stability energy of capacitor.

The wall buckling has been defined as the differences between the mean radiuses⁹¹ of the cylinders consisting of the B and N atoms. It has been shown that the buckling rapidly increases⁹² with decreasing of the tube diameter⁹¹ and are independent of the chirality^92,93.

The (5,5) SWBNNTs in the form of inner cylindrical are  semiconductors due to the existence of an energy gap in the range of  (7.55-9.67) KJ/mol (Table1) which are between  the valence band and the conductor⁹³ band. Those armchair tubes have a direct band gap, similar to the BN structure⁹⁴.

The projected local density of states (PDOS) of B and N are plotted in Fig.2 together with the total DOS for comparison. The data for interaction energy shows that the (5, 5) @ (8, 8) DWBNNTs have a stable form comparing to other systems which yields a suitable charge transfer for the Nano capacitor^92,93.

The calculated values of charge transfer for (5, 5)B-N-NTs @ (7, 7)B-N-NTs, (5,5)B-N-NTs @ (8, 8)B-N-NTs and (5, 5)B-N-NTs @ (9, 9)B-N-NTs and (5, 5)B-N-NTs @ (10, 10)B-N-NTs from inner to outer tubes is found to be  0.53, 0.89, and 0.71 and 0.15electrons respectively, which is an acceptable value (Table1) and it is small for the (5, 5) @ (10, 10) structures due to their unstable forms (Fig 3).

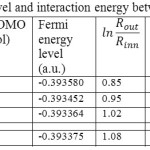Table 1: Gap energy, Fermi level and interaction energy between two layers of DWBNNTs Click here to View table

 

It is indicated in this study that the DWBNNTs can be used as a capacitor due to the semiconductor character, metallic behavior and dielectric function of SWBNNTs. Surprisingly, the optical properties⁹³ of the SWBNNTs optimized by Guo⁹⁴ found that the dielectric function⁹³ could also be divided into two spectral regions⁹⁴, namely, the high and the low energy region -energies these systems⁹⁴.

We show that for the (5, 5) @ (8, 8) the distribution of the accumulated charges in the inner tubes are quantum-mechanically spilled outwards clearly. The capacitance (and) and dielectric constant of the various capacitors have been calculated based eq.4 and are listed in table. 2.

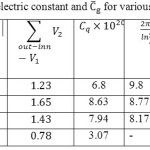Table 2: The dielectric constant and Cg for various DWBNNTs   Click here to View table

 

Conclusion

This work has been investigated the electric polarization and capacitance in a nano-scale coaxial-cylindrical-capacitors which is made of DW boron nitride, (n, n) @ (m, m), using ONIOM model including density-functional and semi empirical methods with the enforced Fermi-energies difference scheme. Despite the fact that the SWBNNTs@ SWBNNTs are a cylindrical capacitor, it has a very sensitive electrical storage compared to SWCNTs@ SWCNTs.

References

1. M. Topsakal, S. Ciraci, Phys. Rev. B, 2012, 85, 045121. 18-20
2. Klein, D. L.;  Roth, R.;  Lim, A. K. L.;  Alivisatos, A. P.; McEuen, P. L.  Nature (London) 1997, 389, 699
   CrossRef
3. Ryo Nakanishi , , Ryo Kitaura , , Jamie H. Warner, Yuta Yamamoto ,, Shigeo Arai, Yasumitsu Miyata, & Hisanori Shinohara , SCIENTIFIC REPORTS | 3 : 1385 2013, DOI 10.1038 /srep01385
4. Dai, H. J.; Rinzler, A. G.; Nikolaev, P.; Thess, A.; Colbert, D. T.; Smalley, R. E. Chem. Phys. Lett. , 1996, 260, 471
   CrossRef
5. Sinnott, S. B.; Andrews, R.; Qian, D.; Rao, A. M.; Mao, Z.; Dickey, E. C.; Derbyshire, F. Chem. Phys. Lett. 1999,  315, 25,
   CrossRef
6. Cheung, C. Li.; Kurtz,A.; Park,H.; Lieber,C.M.; J. Phys. Chem. B,2002, 106, 2429 2433
   CrossRef
7. Z. M. Li, Z. K. Tang, H. J. Liu, N. Wang, C. T. Chan, R. Saito, S. Okada, G. D. Li J. S. Chen, N. Nagasawa, and S. Tsuda, Phys. Rev. Lett. 2001, 87, 127401
   CrossRef
8. Z. K. Tang, L. Zhang, N. Wang, X. X. Zhang, G. H. Wen, G. D. Li, J. N. Wang, C. T. Chan, and P. Sheng, Science, 2001, 292, 2462,
   CrossRef
9. D. Connétable, G. M. Rignanese, J. C. Charlier, and X. Blase, Phys. Rev. Lett. 2005, 94, 015503
   CrossRef
10. P. M. Ajayan and S. Iijima, Nature, 1992, 358, 23
    CrossRef
11. L. F. Sun, S. S. Xie, W. Liu, W. Y. Zhou, and Z. Q. Liu, Nature, 2000, 403, 384
    CrossRef
12. N. Wang, Z. K. Tang, G. D. Li, and J. S. Chen, Nature 408, 50 2000. L. C. Qin, X. Zhao, K. Hirahara, Y. Miyamoto, Y. Ando, and S. Iijima, Nature 2000, 408, 50
    CrossRef
13. X. Zhao, Y. Liu, S. Inoue, T. R. Suzuki, O. Jones, and Y. Ando, Phys. Rev. Lett. 2004, 92, 125502
    CrossRef
14. T. Hayashi, Y. A. Kim, T. Matoba, M. Esaka, K. Nishimura, T. Tsukada, M. Endo, and M. S. Dresselhaus, Nano Lett. 2003 3, 887
    CrossRef
15. A. Rubio, J. L. Corkill, and M. L. Cohen, Phys. Rev. 1994, B 49, 5801
16. N. G. Chopra, R. J. Luyken, and K. Cherrey, Science, 1995, 269, 966
    CrossRef
17. M. Monajjemi J Mol Model. 20(11):2507. doi: 10.1007/s00894-014-2507-y. Epub  Oct 31, 2014
    CrossRef
18. S. Okada, S. Saito, and A. Oshiyama, Phys. Rev. 2002, B 65, 165410
19. Xiang, H., Yang, J., Hou, J. & Zhu, Q. Phys. Rev.2003,  B 68, 035427
20. Chen, Y., Zou, J., Campbell, S. J. & Le Caer, G. Appl. Phys. Lett.2004, 84, 2430–2432,
    CrossRef
21. Kitaura, R. et al. Angew. Chem. Int. Ed. 2009, 48, 8298–8302
    CrossRef
22. Zhao, X.,Ando, Y., Liu, Y., Jinno,M.&Suzuki, T. Phys. Rev. Lett.2003, 90, 187401
    CrossRef
23. Shiozawa, H. Adv. Mater. 2008, 20, 1443–1449
    CrossRef
24. Ando, Y. Chem. Phys. Lett. 2000, 323, 580–585
    CrossRef
25. U. D. Venkateswaran Phys. Rev. B, 2002, 65, 054102
    CrossRef
26. Gugang Chen,S. Bandow,E. R. Ma rgine,C. Nisoli,A. N. Kolmogorov,Vincent H. Crespi,R. Gupta,G.U. Sumanasekera,S. Iijima,and P. C. Eklund ,  PHYSICAL REVIEW LETTERS, 2003, 90, 25 , 257403, 1-4
27. A.   Loiseau   , F.  Willaime  , N. Demoncy, G. Hug and  H. Pascard  , Phys.  Rev.  Lett. 1996, 76, 4737
    CrossRef
28. M. Radosavljevic, J. Appenzeller, V. Derycke , R. Martel, Ph. Avouris, A.      Loiseau, J.-L. Cochon and D. Pigache, Appl. Phys. Lett.2003, 82 ,4131
    CrossRef
29. Y. Miyamoto, A. Rubio, M. L. Cohen and S. G. Louie, Phys. Rev. B, 1994, 50   ,4976
    CrossRef
30. Y. H. Kim, K. J. Chang and S.  G. Louie, Phys. Rev. B, 2001, 63, 205408
    CrossRef
31. K. H. Khoo, M.  S.  C. Mazzoni and S. G. Louie, Phys. Rev. B  2004,69,  201401R
    CrossRef
32. C. W. Chen, M. H. Lee and S. J. Clark, Nanotechnology, 2004, 15, 1837
    CrossRef
33. M.  Ishigami , J.  D. Sau  , S. Aloni, M. L. Cohen and A. Zettl , Phys. Rev. Lett.2005, 94 ,56804
    CrossRef
34. Y. Miyamoto, A. Rubio , M.L. Cohen and S. G. Louie, Phys. Rev. B, 1994, 50   , 4976
    CrossRef
35. E. J. Mele and P. Kral, Phys.  Rev. Lett.2002, 88 , 56803
    CrossRef
36. S. M. Nakhmanson, A. Calzolari,V. Meunier, J. Bernholc and M. B. Nardelli       Phys.  Rev. B,2003, 67, 235406
    CrossRef
37. X. Bai, D. Golberg, Y. Bando, C. Zhi, C. Tang, M. Mitome and K. Kurashima ,Nano Lett.1997,  7, 632
    CrossRef
38. Kazuyuki Uchida, Susumu Okada, Kenji Shiraishi and Atsushi Oshiyama J. Phys.: Condens. Matter,2007, 19 365218
    CrossRef
39. Phys. Rev. B 76, 155436 – Published 30 October  Kazuyuki Uchida, Susumu Okada, Kenji Shiraishi, and Atsushi Oshiyama, 2007
40. Monajjemi, M.;  Boggs, J.E.  J. Phys. Chem. A, 2013, 117, 1670 −1684
    CrossRef
41. Mollaamin, F.; Monajjemi, M, Journal of Computational and Theoretical Nanoscience. 2012, 9 (4) 597-601
    CrossRef
42. Mollaamin, F.; Varmaghani, Z.; Physics and Chemistry of Liquids. 2011, 49 318
    CrossRef
43. Monajjemi, M. Chemical Physics. 2013,425, 29-45,
    CrossRef
44. Monajjemi, M.; Wayne Jr, Robert. Boggs, J.E.  Chemical Physics. 2014,433, 1-11
45. Monajjemi, M.; Mollaamin, F. Journal of Computational and Theoretical Nanoscience, 2012, 9 (12) 2208-2214
    CrossRef
46. Monajjemi, M. Falahati, M.; Mollaamin, F.; Ionics,2013, 19, 155–164
    CrossRef
47. Monajjemi, M.; Mollaamin, F. Journal of Cluster Science, 2012, 23(2), 259-272
    CrossRef
48. Tahan, A.; Monajjemi, M. Acta Biotheor,2011, 59, 291–312, (2011)
    CrossRef
49. Honaparvar , B.; Khalili Hadad ,B.; Ilkhani ,AR.; Mollaamin, F. African Journal of Pharmacy and Pharmacology .2010, 4(8), 521 -529
50. Mollaamin, F.; Monajjemi, M. Physics and Chemistry of Liquids , 2012, 50,  5,  2012, 596–604
51. Monajjemi, M.; Khosravi, M.; Honarparvar, B.; Mollaamin, F.; International Journal of Quantum Chemistry, 2011,111, 2771–2777
    CrossRef
52. Monajjemi, M.  Theor Chem Acc, 2015,134:77 DOI 10.1007/s00214-015-1668-9
    CrossRef
53. Jalilian, H.; Monajjemi, M. Japanese Journal of Applied Physics. 2015,54, 085101
    CrossRef
54. Monajjemi, M.; Khaleghian, M.; Mollaamin, F.   Molecular Simulation. 2010, 36, 11,  865–870
    CrossRef
55. Soofi, N.S., Monajjemi, M,  Oriental Journal of Chemistry. 2016, 32, 11, 2327-2345
56. Elsagh, A., Zare, K., Monajjemi, M. Oriental Journal of Chemistry, 2016, 32, 5, 2585-2598
57. Raoufi, F.; Aghaee, H.; Monajjemi, M.  Oriental Journal of Chemistry, 2016,32, 4, 1839-1858
58. Rahimi, A.;, Monajjemi, M, Oriental Journal of Chemistry, 2016, 32, 6, 2957-296559. Monajjemi, M. Struct Chem. 2012, 23,551–580
59. Monajjemi, M.; Rajaeian, E.; Mollaamin, F.; Naderi, F.; Saki, S. Physics and Chemistry of Liquids. 2008, 46 (3), 299-306
    CrossRef
60. Mollaamin, F.; Gharibe, S.; Monajjemi, M. Int. J. Phy. Sci, 2011, 6, 1496-1500
61. S. Iijima and T. Ichihashi, Nature, 1993, 363, 603
    CrossRef
62. D.S. Bethune, e.B. Kiang, M.S. de Vries, G. Gorman, R Savoy, J. Vazquez, R Beyers, Nature 1993, 363, 605
    CrossRef
63. J.W. Mintmire, B.I. Dunlap, and C.T. White, Phys. Rev. Lett. 1992, 68, 631
    CrossRef
64. R Saito, M. Fujita, G. Dresselhaus, and M.S. Dresselhaus, Appl. Phys. Lett.1992,  60, 2204
    CrossRef
65. G. Bilalbegovic, Phys. Rev. B,1998, 58, 15412
    CrossRef
66. G. Bilalbegovic, Solid State Commun. (2000)
67. G. Bilalbegovic, Computational Materials Science,2000, 18, 333-338
    CrossRef
68. I. S. Gradshteyn and I. M. Ryzhik, Table of Integrals, Series, and Products (Academic Press, New York, (1965)
69. W. A. de Heer, Rev. Mod. Phys.,1993,  65, 611
    CrossRef
70. S. Wang and M. Grifoni, Phys.Rev.B, 2008, 77, 085431
    CrossRef
71. M.W.Schmidt, K.K.Baldridge, J.A.Boatz, S.T.Elbert, M.S.Gordon, J.H.Jensen, S.Koseki, N.Matsunaga, K.A.Nguyen 2004,  14(11) 1347–1363
72. Yan Zhao, Donald G. Truhlar,  Theor Chem Account, 2008,  120 ,215–241
    CrossRef
73. W. Kohn, L. J. Sham, Phys. Rev. 140 A ,1965, 1133-1138
74. J.P. Perdew, K.Burke , Ernzerhof, Phys. Rev. Lett.1996, 77, 3865-3868
    CrossRef
75. D. L. Klein, R. Roth, A. K. L. Lim, A. P. Alivisatos, and P. L. McEuen, Nature (London) 1997, 389 699
    CrossRef
76. Yan Zhao, Donald G. Truhlar, Accounts of Chemical Research, 2008, 41(2) 157-167
    CrossRef
77. C.E.Check, T.M.Gilbert, J. Org. Chem, 2005, 70 ,9828–9834
    CrossRef
78. S.Grimme, Seemingly. Angew. Chem., Int. Ed.2006, 45 ,4460–4464
    CrossRef
79. B.H. Besler, K.M. Merz, P.A. Kollman, J. comp. Chem.1990, 11 ,431
80. L.E. Chirlian , M.M. Francl, J.comp.chem.1987, 8 ,894
81. Brneman GM, Wiberg KB ,J. Comp Chem, 1990, 11: 361
    CrossRef
82. Martin F, Zipse H . J Comp Chem. 2005, 26: 97 ,105
83. Monajjemi M, Lee VS, Khaleghian M, Honarparvar B, Mollaamin F ,J. Phys. Chem. C, 2010, 114 15315
    CrossRef
84. M. Monajjemi M , Khaleghian M J Clust Sci, 2011, 22:673–692
    CrossRef
85. Monajjemi M Struct. Chem.2012,  23: 551
    CrossRef
86. Balderchi, A, Baroni S,  Resta R Phys. Rev. Lett 1998, 61: 173
87. Tian Lu, Feiwu Chen, Acta Chim. Sinica, 2011, 69, 2393-2406
88. Tian Lu, Feiwu Chen, J. Mol. Graph. Model. 2012, 38, 314-323
    CrossRef
89. Tian Lu, Feiwu Chen, Multiwfn:  J. Comp. Chem.2012, 33, 580-592
    CrossRef
90. X. Blase, Phys. Rev. Lett.1994, 72, 1878
    CrossRef
91. E. Hernández, C. Goze, P. Bernier, and A. Rubio, Phys. Rev. Lett.1998,  80, 4502
    CrossRef
92. L. Wirtz, A. Rubio, R. A. Concha, and A. Loiseau, Phys. Rev. B, 2003,   68, 045425
    CrossRef
93. G.Y. Guo, J.C. Lin, Phys. Rev. B, 2005, 71, 165402
    CrossRef

---

This work is licensed under a Creative Commons Attribution 4.0 International License.