Solvent Effects on the Mechanistic of Ketene and Halogenated Ketene Cycloadditions with Cyclopentadiene: A DFT Study
Nasrin Farahani1 and Seyed Majid Musavi2
1Department of Chemistry, Buinzahra Branch, Islamic Azad University, Buinzahra, Iran.
2Department of Chemistry, Payame Noor University, Qom 311-37185, Iran.
Corresponding Author E-mail: moosavi_majid@yahoo.com
DOI : http://dx.doi.org/10.13005/ojc/330326
The energetic and activation barriers for 4 possible [2+2] and [4+2] cycloadditions of ketene and dihaloketenes with cyclopentadiene are investigated at B3LYP/6-31G* level of theory. Three solvents including DMSO, CCl4 and water, using the CPCM model, are considered and their results are compared to those of gas phase. The entire studied cycloadditions take place via clear asynchronous TSs. For the parent ketene, all solvents stabilize the reactants within the range of 9.4-13.7 kcal/mol and reduce the thermodynamic achievability of this reaction (∆E=-18.4, -10.9, -11.6 and -12.8 kcal/mol for gas phase, CCl4, DMSO and H2O, respectively, for [2+2] across C=C) and the energy barriers are increased to the maximum of 6.1 kcal/mol. In contrast, for dihaloketenes all solvents make the thermodynamics less favorite by decreasing the exoergicity (within 1-5 kcal/mol), however, most of reaction pathways become kinetically favored by lowering the energy barriers (within 1-7 kcal/mol) in the presence of polar solvents. The nonpolar solvent CCl4 behaves like that of gas phase. Moreover, the preference of two-step cycloaddition via [3+3] sigmatropic rearrangement is reduced in the presence of solvents. The ultimate effect is pertaining to dichloroketen where it prefers the routine one-step cycloaddition pathway in H2O like that observed for the parent ketene.
KEYWORDS:Dihaloketene; Cycloaddition; Dielectric constant; Density functional theory; Dielse-Alder
Download this article as:| Copy the following to cite this article: Farahani N, Musavi S. M. Solvent Effects on the Mechanistic of Ketene and Halogenated Ketene Cycloadditions with Cyclopentadiene: A DFT Study. Orient J Chem 2017;33(3). |
| Copy the following to cite this URL: Farahani N, Musavi S. M. Solvent Effects on the Mechanistic of Ketene and Halogenated Ketene Cycloadditions with Cyclopentadiene: A DFT Study. Orient J Chem 2017;33(3). Available from: http://www.orientjchem.org/?p=33317 |
Introduction
Ketene chemistry started at the beginning of the previous century and subsequently it has extensively blossomed because of its theoretical significance as well as its utility in the organic synthesis [1, 2]. The most characteristic reaction of ketenes is the cycloaddition, which is a powerful method to generate four membered ring heterocyclics. Ketenes mainly participate in [2+2] cycloadditions with a variety of dienophiles across the C=C, C=O, C=N, C=S, N=N, N=O, N=S, and P=N bonds [3]. Ketenes prefer to primarily form vinylcyclobutanone in the reaction with dienes which many reports argued their mechanisms by a single step [2+2] or by a [4+2] following a [3,3] rearrangement [4-9]. Despite the large number of reports on the gas phase cycloadditions of ketenes [10] theoretical investigations on the roles of solvents in the reaction mechanisms appear to be limited. A general belief is that polar solvents stabilize the zwitterionic intermediates, consequently altering the mechanism from a concerted process in the gas phase to a stepwise one in solution via a more stable zwitterionic intermediate [11]. This is qualitatively in accord with experimental observations. However, quantitatively the magnitude of solvent effects on the free energy of activation has been a fundamental question [12]. Moreover, the accuracy of theoretical models in such reactions is a big problem for the computational study. For instance, SCRF and the more accurate self-consistent isodensity polarizable continuum model (SCIPCM) calculations at the HF/6-31G* and B3LYP/6-31G* levels predict the solvent effects lowering the activation energy of the cycloaddition of 1,1-dicyanoethylene (DCNE) and methyl vinyl ether (MVE) by 10-13 kcal/mol on going from CCl4 to CH3CN [13] which is substantially larger than the observed data of about 5 kcal/mol. Many researchers studied the stereo-divergent outcome of the cycloadditions of ketenes and imines theoretically and experimentally. Accordingly, Cossio et al stated that the solvent effects should be taken into account and suggested that the polarity of the solvent enhances the diastereomeric excess of the reaction [14]. Moreover, the reaction of ketene with formaldimine at the B3LYP/6-31G* level [15] showed a different reaction path compared to previous report of Sordo et al [16, 17] where an intermediate was located when the solvent effect is added during the IRC calculation. This again confirms the significance of solvents in the reaction pathways of ketene cycloadditions.
As a consequence, it would be of interest to test the available solvation methodology on this inspiring reaction. For this purpose, we have investigated roles of three solvents on the structures and mechanisms of the [2+2] and [4+2] cycloadditions between ketene and dihalogenated ketene analogues with cyclopentadiene (cp) along four different reaction pathways previously outlined [18] (Figure 1).
![Figure 1: Different pathways for [2+2] and [4+2] cycloadditions of ketene and dihaloketenes with cp](http://www.orientjchem.org/wp-content/uploads/2017/05/Vol33No3_Solv_Nasr_fig1-150x150.jpg) |
Figure 1: Different pathways for [2+2] and [4+2] cycloadditions of ketene and dihaloketenes with cp |
Computational Methods
The molecular orbital calculations were carried out using Gaussian 03 program package [19]. All geometry optimizations are performed at the B3LYP/6-31G* level (the hybrid three-parameter functional developed by Becke [20]) using the 6-31G* basis set [21]. Intrinsic reaction coordinate (IRC) calculations [22] are performed to connect the transition states to their respective minima in all cases. Frequency calculations verified the identity of each stationary point as a minimum or a transition state. Zero-point vibrational energies have been computed and have not been scaled. The polarizable continuum (PCM) and CPCM model [23] are employed to consider the effect of the solvent on the reactions of interest at the B3LYP/CPCM/6-31+G* level of theory using the optimized geometries along the minimum energy pathway. Natural bond orbital (NBO) calculations [24] have been done at B3LYP/6-311++G** level. The transition states (TSs) linking the initial and final structures found using the reactant products quasi synchronous transient (QST2) algorithm [25].
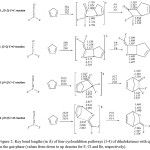 |
Figure 2: Key bond lengths (in Å) of four cycloaddition pathways (1-4) of dihaloketenes with cp in the gas-phase (values from down to up denotes for F, Cl and Br, respectively). Click here to View figure |
Computational Methods
The molecular orbital calculations were carried out using Gaussian 03 program package [19]. All geometry optimizations are performed at the B3LYP/6-31G* level (the hybrid three-parameter functional developed by Becke [20]) using the 6-31G* basis set [21]. Intrinsic reaction coordinate (IRC) calculations [22] are performed to connect the transition states to their respective minima in all cases. Frequency calculations verified the identity of each stationary point as a minimum or a transition state. Zero-point vibrational energies have been computed and have not been scaled. The polarizable continuum (PCM) and CPCM model [23] are employed to consider the effect of the solvent on the reactions of interest at the B3LYP/CPCM/6-31+G* level of theory using the optimized geometries along the minimum energy pathway. Natural bond orbital (NBO) calculations [24] have been done at B3LYP/6-311++G** level. The transition states (TSs) linking the initial and final structures found using the reactant products quasi synchronous transient (QST2) algorithm [25].
Table 1: Calculated MOs energies, au; as well as the differences between FMO energies, kcal/mol; for cycloadditions under studied.
|
Interacting MOs |
Phase |
HOMO |
LUMO |
LUMO + 1 |
H- L |
H-L+1 |
|
HOMO (cp)-LUMO (ketene) |
Water |
-0.22632 |
-0.04810 |
0.00148 |
111.8 |
142.9 |
|
CCl4 |
-0.22338 |
-0.04968 |
0.00099 |
108.9 |
140.75 |
|
|
DMSO |
-0.22454 |
-0.04965 |
0.00110 |
109.7 |
141.5 |
|
|
Gas |
-0.222 |
-0.050 |
0.001 |
108.23 |
139.93 |
|
|
LUMO (cp)-HOMO (ketene) |
Water |
-0.25355 |
-0.02848 |
0.01565 |
141.2 |
168.9 |
|
CCl4 |
-0.25378 |
-0.02708 |
0.01532 |
142.2 |
168.8 |
|
|
DMSO |
-0.25385 |
-0.02765 |
0.01590 |
141.9 |
169.2 |
|
|
Gas |
-0.253 |
-0.026 |
0.014 |
142.5 |
167.5 |
|
|
HOMO (cp)-LUMO (Difluoroketene) |
Water |
-0.22632 |
-0.10970 |
-0.00212 |
73.1 |
140.6 |
|
CCl4 |
-0.22338 |
-0.11424 |
-0.00537 |
68.4 |
136.8 |
|
|
DMSO |
-0.22454 |
-0.11261 |
-0.00361 |
70.2 |
138.6 |
|
|
Gas |
-0.222 |
-0.116 |
-0.007 |
66.7 |
134.9 |
|
|
LUMO (cp)-HOMO (difluoroketene) |
Water |
-0.25107 |
-0.02848 |
0.01565 |
139.6 |
167.3 |
|
CCl4 |
-0.25486 |
-0.02708 |
0.01532 |
142.9 |
169.5 |
|
|
DMSO |
-0.25334 |
-0.02765 |
0.01590 |
141.6 |
168.9 |
|
|
Gas |
-0.256 |
-0.026 |
0.014 |
144.4 |
169.4 |
|
|
HOMO (cp)-LUMO (Dichloroketene) |
Water |
-0.22632 |
-0.10558 |
-0.03492 |
75.7 |
120.1 |
|
CCl4 |
-0.22338 |
-0.10796 |
-0.03682 |
72.4 |
117.0 |
|
|
DMSO |
-0.22454 |
-0.10746 |
-0.03604 |
73.4 |
118.2 |
|
|
Gas |
-0.222 |
-0.108 |
-0.037 |
71.3 |
116.0 |
|
|
LUMO (cp)-HOMO (Dichloroketene) |
Water |
-0.24929 |
-0.02848 |
0.01565 |
138.5 |
166.2 |
|
CCl4 |
-0.25102 |
-0.02708 |
0.01532 |
140.5 |
167.1 |
|
|
DMSO |
-0.25048 |
-0.02765 |
0.01590 |
139.8 |
167.1 |
|
|
Gas |
-0.251 |
-0.026 |
0.014 |
141.3 |
166.2 |
|
|
HOMO (cp)-LUMO (Dibromoketene) |
Water |
-0.22632 |
-0.10777 |
-0.06087 |
74.3 |
103.8 |
|
CCl4 |
-0.22338 |
-0.10928 |
-0.06299 |
71.5 |
100.6 |
|
|
DMSO |
-0.22454 |
-0.10906 |
-0.06226 |
72.4 |
101.8 |
|
|
Gas |
-0.222 |
-0.109 |
-0.063 |
70.8 |
99.7 |
|
|
LUMO (cp)-HOMO (Dibromoketene) |
Water |
-0.24553 |
-0.02848 |
0.01565 |
136.1 |
163.8 |
|
CCl4 |
-0.24659 |
-0.02708 |
0.01532 |
137.7 |
164.3 |
|
|
DMSO |
-0.24637 |
-0.02765 |
0.01590 |
137.2 |
164.5 |
|
|
Gas |
-0.246 |
-0.026 |
0.014 |
138.3 |
163.1 |
The [2+2] cycloadditions of parent ketene with cp across the C=C bond of ketene leads to the cycloadduct P1 after passing thorough TS1 (Figure 3A). This is a moderate exoergic reaction (∆E= -18.4 kcal/mol) with a high energy barrier (∆E‡=18.0 kcal/mol). All solvents stabilize the reactants within the range of 9.4-13.7 kcal/mol and reduce the thermodynamic achievability of this reaction (∆E= -10.9, -11.6 and -12.8 kcal/mol for CCl4, DMSO and H2O, respectively). On the other hand, the energy barrier is increased to the maximum of 6.1 kcal/mol. Interestingly, the least polar solvent exerts the most unfortunate thermodynamic and kinetic conditions for this reaction.
In the other alternative pathway, the [2+2] cycloadditions of parent ketene with cp across the C=O bond of ketene leads to the cycloadduct P2 after passing thorough TS2 (Fig. 3B). This is a low exoergic reaction (∆E= -1.8 kcal/mol) with a very high energy barrier (∆E‡=32.6 kcal/mol). Consequently, this path of reaction has a lower significance in the competition. Again, all solvents reduce the thermodynamic achievability of this reaction by switching the reactions to endoergic ones (∆E= 5.7, 5.13 and 2.8 kcal/mol for CCl4, DMSO and H2O, respectively). On the other hand, the energy barrier is increased to 37.8 kcal/mol for CCl4 and 34.7 kcal/mol for DMSO while decreased to 29.8 kcal/mol for H2O. Again, the least polar solvent exerts the most unfortunate thermodynamic and kinetic conditions for this reaction. In general, the [2+2] cycloaddition across the C=C and C=O bond of ketene would be of less favorite in the solvents compared to gas phase.
![Figure 3: Relative reaction energies of [2+2] cycloadition reaction across C=C bond of ketene (A) and [2+2] cycloadition reaction across C=O bond of ketene (B) in the gas phase and solvents.](http://www.orientjchem.org/wp-content/uploads/2017/05/Vol33No3_Solv_Nasr_fig37-150x150.jpg) |
Figure 3: Relative reaction energies of [2+2] cycloadition reaction across C=C bond of ketene (A) and [2+2] cycloadition reaction across C=O bond of ketene (B) in the gas phase and solvents. Click here to View figure |
The [4+2] Cycloadditions Across the C=C and C=O Bond of Ketene
The concerted [4+2] cycloaddition, namely Dielse-Alder reaction, across the C=C bond of the ketene with cp yields cyclopentanones P3 in one step after passing through the corresponding TS3 (Figure 4A).This is a moderate exoergic reaction (∆E= -23.3 kcal/mol) with a high energy barrier (∆E‡=25.9 kcal/mol). All solvents reduce the thermodynamic achievability of this reaction (∆E= -15.9, -16.8 and -18.2 kcal/mol for CCl4, DMSO and H2O, respectively). On the other hand, the energy barrier is increased to the maximum of 6.0 kcal/mol. Again, the least polar solvent exerts the most unfortunate thermodynamic and kinetic conditions for this reaction.
The last possible reaction mode is the concerted [4+2] cycloaddition across the C=O bond of the ketene with cp which leads to a five-membered ring ether P4 after passing through the corresponding TS4 (Figure 4B). This is a low exoergic reaction (∆E= -3.7 kcal/mol) with a high energy barrier (∆E‡=17.6 kcal/mol). All solvents reduce the thermodynamic achievability of this reaction by switching them to endoergic ones (∆E= 4.1, 3.7 and 2.2 kcal/mol for CCl4, DMSO and H2O, respectively). On the other hand, the energy barrier is increased to nearly 6.0 kcal/mol. Again, the least polar solvent exerts the most unfortunate thermodynamic and kinetic conditions for this reaction.
![Figure 4: Relative reaction energies of [4+2] cycloadition reaction across C=C bond of ketene (A) and [4+2] cycloadition reaction across C=O bond of ketene (B) in the gas phase (red line) and solvents.](http://www.orientjchem.org/wp-content/uploads/2017/05/Vol33No3_Solv_Nasr_fig44-150x150.jpg) |
Figure 4: Relative reaction energies of [4+2] cycloadition reaction across C=C bond of ketene (A) and [4+2] cycloadition reaction across C=O bond of ketene (B) in the gas phase (red line) and solvents. Click here to View figure |
The [3,3] Sigmatropic Rearrangement of Ketene
In this section, the possibility of a [3,3] sigmatropic rearrangement on the initially formed cycloadducts of [4+2] reaction across the C=O bond of the ketene [26] is considered. This rearrangement can result in a [2+2] product across the C=C bond of the ketene as the final transformation (Figure 5). Calculated data show that reactants convert to an unstable bicyclic six-membered ether (∆E= -3.7 kcal/mol) after passing through a relatively high energy barrier (∆E‡=17.6 kcal/mol) which passes through the second barrier of 21.7 kcal/mol to generate the high stable cyclobutanone (∆E= -18.4 kcal/mol). In a comparison with the one-step [2+2] cycloaddition, however it is apparent that for the parent ketene the one-step pathway is preferred over the mentioned two-step pathway due to the similarity of barrier heights. Again, all solvents increase the first barrier energies within the range of 1.1-6.5 kcal/mol (∆E1‡=24.1, 22.4, and 18.7 kcal/mol for CCl4, DMSO and H2O, respectively) by stabilizing the corresponding reactants. Concurrently, the most polar solvent reduces the stability of intermediate by 5.9 kcal/mol and the second energy barrier somewhat increases by CCl4 and DMSO and slightly decreases by H2O while all the exoergicities are reduced sharply by solvents (∆E=-10.9, -11.7, and -12.9 kcal/mol for CCl4, DMSO and H2O, respectively). In other words, the preference of two-step cycloaddition is reduced in the presence of solvents.
The [3,3] Sigmatropic Rearrangement of Ketene
In this section, the possibility of a [3,3] sigmatropic rearrangement on the initially formed cycloadducts of [4+2] reaction across the C=O bond of the ketene [26] is considered. This rearrangement can result in a [2+2] product across the C=C bond of the ketene as the final transformation (Figure 5). Calculated data show that reactants convert to an unstable bicyclic six-membered ether (∆E= -3.7 kcal/mol) after passing through a relatively high energy barrier (∆E‡=17.6 kcal/mol) which passes through the second barrier of 21.7 kcal/mol to generate the high stable cyclobutanone (∆E= -18.4 kcal/mol). In a comparison with the one-step [2+2] cycloaddition, however it is apparent that for the parent ketene the one-step pathway is preferred over the mentioned two-step pathway due to the similarity of barrier heights. Again, all solvents increase the first barrier energies within the range of 1.1-6.5 kcal/mol (∆E1‡=24.1, 22.4, and 18.7 kcal/mol for CCl4, DMSO and H2O, respectively) by stabilizing the corresponding reactants. Concurrently, the most polar solvent reduces the stability of intermediate by 5.9 kcal/mol and the second energy barrier somewhat increases by CCl4 and DMSO and slightly decreases by H2O while all the exoergicities are reduced sharply by solvents (∆E=-10.9, -11.7, and -12.9 kcal/mol for CCl4, DMSO and H2O, respectively). In other words, the preference of two-step cycloaddition is reduced in the presence of solvents.
![Figure 5: Relative energies, kcal/mol; for the proposed [3,3] sigmatropic rearrangement of ketene and dihaloketenes with cp in the gas phase and solvents.](http://www.orientjchem.org/wp-content/uploads/2017/05/Vol33No3_Solv_Nasr_fig51-150x150.jpg) |
Figure 5: Relative energies, kcal/mol; for the proposed [3,3] sigmatropic rearrangement of ketene and dihaloketenes with cp in the gas phase and solvents.
|
Table 2: The calculated energetics (total energy E and relative energy Er/ kcal mol-1) in the gas-phase and in different solvents for the cycloadditions of dihaloketenes with cp.
|
Phase |
Gas |
DMO |
CCl4 |
Water |
||||
|
Reaction mode |
E |
Er |
E |
Er |
E |
Er |
E |
Er |
| Diflouroketene+ Cp |
-342082.8 |
0 |
-342090.7 |
-7.86 |
-342089.8 |
-7.00 |
-342095.9 |
-13.05 |
|
TS[2+2] C=C |
-342078.9 |
3.89 |
-342084.9 |
-2.07 |
-342082.0 |
0.83 |
-342091.0 |
-8.24 |
|
P[2+2] C=C |
-342131.9 |
-49.07 |
-342136.2 |
-53.39 |
-342134.1 |
-51.33 |
-342140.9 |
-58.14 |
|
TS[2+2] C=O |
-342076.1 |
6.74 |
-342085.0 |
-2.14 |
-342080.4 |
2.35 |
-342092.9 |
-10.06 |
|
P[2+2] C=O |
-342106.3 |
-23.50 |
-342110.5 |
-27.67 |
-342108.5 |
-25.68 |
-342116.1 |
-33.34 |
|
TS[4+2] C=C |
-342074.4 |
8.39 |
-342082.6 |
0.19 |
-342078.4 |
4.36 |
-342091.4 |
-8.57 |
|
P[4+2] C=C |
-342136.6 |
-53.75 |
-342141.6 |
-58.76 |
-342139.2 |
-56.36 |
-342146.5 |
-63.65 |
|
TS[4+2]C=O |
-342082.7 |
0.13 |
-342089.1 |
-6.27 |
-342086.0 |
-3.15 |
-342095.4 |
-12.57 |
|
P[4+2] C=O |
-342109.4 |
-26.58 |
-342113.2 |
-30.36 |
-342111.4 |
-28.57 |
-342118.0 |
-35.23 |
| Dichloroketene+ Cp |
-794339.0 |
0 |
-794346.6 |
-7.58 |
-794345.8 |
-6.83 |
-794349.6 |
-10.57 |
|
TS[2+2] C=C |
-794329.3 |
9.72 |
-794336.2 |
2.76 |
-794332.8 |
6.21 |
-794343.3 |
-4.31 |
|
P[2+2] C=C |
-794370.9 |
-31.88 |
-794374.9 |
-35.93 |
-794373.0 |
-33.95 |
-794380.1 |
-41.06 |
|
TS[2+2] C=O |
-794324.5 |
14.49 |
-794333.7 |
5.32 |
-794329.0 |
10.01 |
-794342.4 |
-3.43 |
|
P[2+2] C=O |
-794354.1 |
-15.10 |
-794358.3 |
-19.29 |
-794356.3 |
-17.27 |
-794363.7 |
-24.71 |
|
TS[4+2] C=C |
-794320.0 |
19.03 |
-794326.9 |
12.10 |
-794323.4 |
15.59 |
-794333.4 |
5.64 |
|
P[4+2] C=C |
-794373.1 |
-34.05 |
-794377.5 |
-38.54 |
-794375.4 |
-36.36 |
-794382.6 |
-43.61 |
|
TS[4+2] C=O |
-794333.3 |
5.73 |
-794337.7 |
1.25 |
-794335.6 |
3.40 |
-794342.1 |
-3.07 |
|
P[4+2] C=O |
-794355.8 |
-16.82 |
-794359.7 |
-20.67 |
-794357.8 |
-18.83 |
-794364.6 |
-25.63 |
| Dibromoketene+ Cp |
-3444306.2 |
0 |
-3444313.9 |
-7.65 |
-3444313.1 |
-6.87 |
-3444316.9 |
-10.68 |
|
TS[2+2] C=C |
-3444297.1 |
9.13 |
-3444303.8 |
2.45 |
-3444300.5 |
5.78 |
-3444311.1 |
-4.89 |
|
P[2+2] C=C |
-3444345.1 |
-38.88 |
-3444349.1 |
-42.86 |
-3444347.2 |
-40.95 |
-3444354.1 |
-47.89 |
|
TS[2+2] C=O |
-3444294.3 |
11.95 |
-3444303.6 |
2.63 |
-3444298.8 |
7.41 |
-3444313.0 |
-6.80 |
|
P[2+2] C=O |
-3444323.6 |
-17.40 |
-3444327.7 |
-21.46 |
-3444325.8 |
-19.52 |
-3444333.0 |
-26.75 |
|
TS[4+2] C=C |
-3444291.6 |
14.64 |
-3444298.9 |
7.34 |
-3444295.2 |
11.02 |
-3444306.6 |
-0.38 |
|
P[4+2] C=C |
-3444347.4 |
-41.15 |
-3444351.8 |
-45.50 |
-3444349.7 |
-43.42 |
-3444356.8 |
-50.57 |
|
TS[4+2]C=O |
-3444303.2 |
2.99 |
-3444308.1 |
-1.89 |
-3444305.8 |
0.46 |
-3444313.6 |
-7.38 |
|
P[4+2] C=O |
-3444325.5 |
-19.29 |
-3444329.3 |
-23.05 |
-3444327.5 |
-21.26 |
-3444334.3 |
-28.07 |
|
[3,3] sigmatropic
|
-3444306.7 |
-0.43 |
-3444312.6 |
-6.33 |
-3444309.7 |
-3.43 |
-3444319.3 |
-13.08 |
Table 3: The B3LYP/6-31G(d,p) calculated energetic data for one-step and two-step [3,3] sigmatropic rearrangements of ketene and dihaloketenes with cp at four media.
|
|
|
∆E/kcal |
mol-1 | |
|
|
Ketene |
Diflouroketene |
Dichloroketene |
Dibromoketene |
|
R→TS |
18.0 |
3.9 |
9.7 |
9.1 |
|
24.2 |
7.8 |
13.0 |
12.6 |
|
|
22.0 |
5.8 |
10.3 |
10.0 |
|
|
18.4 |
4.8 |
6.2 |
5.8 |
|
|
R→TS1 |
17.6 |
0.1 |
5.7 |
3.0 |
|
24.1 |
3.8 |
10.2 |
7.33 |
|
|
22.4 |
1.6 |
8.8 |
5.7 |
|
|
19.7 |
0.5 |
7.5 |
3.3 |
|
|
R→Int |
-3.7 |
-26.6 |
-16.8 |
-19.3 |
|
4.1 |
-21.5 |
-12.0 |
-14.4 |
|
|
3.7 |
-22.5 |
-13.1 |
-15.4 |
|
|
2.2 |
-22.2 |
-15.0 |
-17.4 |
|
|
Int→TS2 |
21.7 |
18.1 |
20.5 |
19.7 |
|
20.0 |
17.1 |
19.2 |
17.8 |
|
|
18.3 |
15.9 |
18.0 |
16.7 |
|
|
16.2 |
14.1 |
15.9 |
15.0 |
|
|
R→P |
-18.4 |
-49.1 |
-31.9 |
-38.9 |
|
-10.9 |
-44.3 |
-27.0 |
-34.1 |
|
|
-16.7 |
-45.5 |
-28.3 |
-35.2 |
|
|
-12.9 |
-15.5 |
-30.4 |
-37.2 |
Conclusions
Dielse-Alder [4+2] and Staudinger [2+2] reactions between ketene and dihaloketenes with cyclopentadiene are studied in four different reaction pathways and four different media (gas phase, CCl4, DMSO and H2O) at B3LYP/6-31G* level. For the parent ketene, [2+2] across the C=C and [4+2] across the C=C bond of ketene are high exoergic (∆E=-23.2 kcal/mol and -18.4 kcal/mol, respectively) while the two other pathways including [2+2] across the C=O and [4+2] across the C=O bond of ketene are somewhat endoergic. The activation barriers for these reaction modes change in the range of 17.5- 32.6 kcal/mol. Halogens substitution facilitates the cycloadditions by increasing the exoergicity and reducing the activation barriers. All cycloadditions take place via clear asynchronous TSs. For the parent ketene, all solvents stabilize the reactants by 9.4-13.7 kcal/mol and reduce the exoergicity (e.g. ∆E=-18.4, -10.9, -11.6 and -12.8 kcal/mol for gas phase, CCl4, DMSO and H2O, respectively, for [2+2] across C=C) and the energy barriers are increased to the maximum of 6.1 kcal/mol. In contrast, for dihaloketenes all solvents make the thermodynamics less favorite by decreasing the exoergicity (within 1-5 kcal/mol), however, most of reaction pathways become kinetically favored by lowering the energy barriers (within 1-7 kcal/mol) in the presence of polar solvents. The nonpolar solvent CCl4 behaves like that of gas phase. Furthermore, the preference of two-step cycloaddition via the [3+3] sigmatropic rearrangement is reduced in the presence of solvents. Finally, for dichloroketene the routine single-step cycloaddition appears as the preferred pathway in H2O like that observed for the parent ketene. Our findings denote the polar, but not zwitterionic, cycloadditions in this study.
Acknowledgements
The research supported by the Research Council of the Islamic Azad University Buinzahra Branch.
References
- Beaker, P.; Bittman, R.; Ciganek, E.; Curran, D.; Hegedus, L.; Joyce, R. M.; Kelly, R.C.; Overman, L. E.; Paquette, L.A.; Press, J.B.; Poush, W.; Smith, A.B.; Uskokovic, M.; Wiley, J.D. Organic Reactions, , John Wiley and Sons, Inc., New York. 1994, 45
- Tidwell, T.T. Ketenes, John Wiley and Sons, Inc., New York. 1995,
- Ulrich, H. Cycloaddition Reactions of Heterocumulenes, , Academic Press Inc., New York. 1967
- Holder, R.W.; Graf, N.A.; Duesler, E.; Moss, J.C. J. Am. Chem. Soc. 1983, 105, 2929-2931.
CrossRef - Schmittel, M.; Von Seggern, H. J. Am. Chem. Soc. 1993, 115, 2165-2177.
CrossRef - Yamabe, S.; Dai, T. J. Am. Chem. Soc. 1996, 118, 6518-6519.
CrossRef - Machiguchi, T.; Hasegawa, T.; Ishiwata, A.; Terashima, S.; Yamabe, S.; Minato, T. J. Am. Chem. Soc. 1999, 121, 4771-4786.
CrossRef - Mayr, H.; Heigl, U.W. J. Chem. Soc. Chem. Commun. 1987, 1804-1805.
CrossRef - Rubio, M.F.; Cruz, F.J.; Galicia, G. R. J. Mex. Chem. Soc. 2010, 54, 209-215.
- Allen, A.D.; Tidwell, T.T. Chem. Rev. 2013, 113, 7287-7342.
CrossRef - Visser, P.; Zuhse, R.; Wong, M.W.; Wentrup, C. J. Am. Chem. Soc. 1996, 118, 12598-12602.
CrossRef - Truong, T.N. J. Phys. Chem. B 1998, 102, 7877-7881.
CrossRef - Lim, D.; Jorgensen, W.L. J. Phys. Chem. 1996,100, 17490-17500.
CrossRef - Arrieta, A. Lecea, B.; Cossio, F.P. J. Org. Chem. 1998, 63, 5869-5876.
CrossRef - Zhou, C.; Birney D.M. J. Am. Chem. Soc. 2002, 124, 5231-5241.
CrossRef - Sordo, J. A.; Gonzalez, J.; Sordo, T.L. J. Am. Chem. Soc. 1992, 114, 6249-6251.
CrossRef - Lopez, R.; Sordo, T.L.; A. Sordo, J.; Gonzalez, J. J. Org. Chem. 1993, 58, 7036-7037.
CrossRef - Musavi, S.M.; Amani, J.; Omidian, N. Tetrahedron 2014, 70, 708-719.
CrossRef - Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb, M. A.; Cheeseman, J. R.; Montgomery, Jr., J. A.; Vreven, T.; Kudin, K. N.; Burant, J. C.; Millam, J. M.; Iyengar, S. S.; Tomasi, J.; Barone, V.; Mennucci, B.; Cossi, M.; Scalmani, G.; Rega, N.; Petersson, G. A.; Nakatsuji, H.; Hada, M.; Ehara, M.; Toyota, K.; Fukuda, R.; Hasegawa, J.; Ishida, M.; Nakajima, T.; Honda, Y.; Kitao, O.; Nakai, H.; Klene, M.; Li, X.; Knox, J. E.; Hratchian, H. P.; Cross, J. B.; Bakken, V.; Adamo, C.; Jaramillo, J.; Gomperts, R.; Stratmann, R. E.; Yazyev, O.; Austin, A. J.; Cammi, R.; Pomelli, C.; Ochterski, J. W.; Ayala, P. Y.; Morokuma, K.; Voth, G. A.; Salvador, P.; Dannenberg, J. J.; Zakrzewski, V. G.; Dapprich, S.; Daniels, A. D.; Strain, M. C.; Farkas, O.; Malick, D. K.; Rabuck, A. D.; Raghavachari, K.; Foresman, J. B.; Ortiz, J. V.; Cui, Q.; Baboul, A. G.; Clifford, S.; Cioslowski, J.; Stefanov, B. B.; Liu, G.; Liashenko, A.; Piskorz, P.; Komaromi, I.; Martin, R. L.; Fox, D. J.; Keith, T.; Al-Laham, M. A.; Peng, C. Y.; Nanayakkara, A.; Challacombe, M.; Gill, P. M. W.; Johnson, B.; Chen, W.; Wong, M. W.; Gonzalez, C.; Pople, J. A. 2004, Gaussian, Inc., Wallingford CT, Gaussian, Inc., Gaussian 03, Revision C.02, Wallingford CT.
- Becke, A. D. J. Chem. Phys. 1993, 98, 5648-5652.
CrossRef - Hariharan, P.C.; Pople, J.A. Theor. Chim. Acta. 1973, 28, 213-222.
CrossRef - Gonzalez, C.; Schlegel, H. B. J. Phys. Chem. 1990, 94, 5523-5527.
CrossRef - Peng, C.; Ayala, P.Y.; Schlegel, H.B.; Frisch, M. J. J. Comp. Chem. 1996, 17, 49-56.
CrossRef - Weinhold, F.; Carpenter, J.E. The Natural Bond Orbital Lewis Structure Concept for Molecules, Radicals, and Radical Ions, in, Naaman R.; Vager Z. (eds.), The Structure of Small Molecules and Ions. Plenum, New York, 1988, 227-236.
CrossRef - Miertus, S.; Scrocco, E.; Tomasi, J. J. Chem. Phys. 1981, 55, 117-129.
- Fukui, K.; Yonezawa, T.; Shingu, H. J. Chem. Phys. 1952, 20, 722-725.
CrossRef

This work is licensed under a Creative Commons Attribution 4.0 International License.









