Theoretical Studies of Solvent Effect for Oxindole Derivatives using Polarizable Continuum Model

Introduction

Oxindoles are useful building blocks for indole chemistry. Heterocyclic compounds containing 5 to 6 membered ring are important for their diverse biological activities¹. The chemistry of oxazolidinone and its derivatives have received considerable attention owing to their synthetic and biological importance. The first oxindole obtained from the condensation of isatin with indole is 3, 3-bis(indolyl)indoline-2- prepared by Seidel in 1950. During recent years some methods have been reported for the condensation of electron-rich hetero aromatics such as indoles and pyrroles with isatins to afford their oxindole derivatives. Oxindole frameworks are found in many bioactive compounds and natural products. Due to this synthetic methods and transformations of oxindole skeletons have been extensively investigated^2-5. The naturally occurring oxindole derivative convolutamydine has been found to exhibit potent activity in the differentiation of HL-60 human plomyelocytic leukemic cells. The varied biological activities of oxindole derivatives have attracted the synthetic chemists to a number of synthetic strategies^6-9. Plant hormone, indole 3-acetic acid and animal hormone, melatonin, a potent anti-oxidant are the two most important indole derivatives. Few oxindole derivatives found in marine fish and shell fish are reported to have radical scavenging activity in comparison to the powerful anti-oxidants like uric acid and indole in humans. The solubility in different solvents is an important parameter for assessing the bioavailability of pharmaceutically important organic compounds as well as in the synthesis of these compounds. Realizing the importance of the oxindole derivatives, we carried out the solvation analysis of four oxindole compounds. The standard state of free energy solvation is a fundamental quantity that describes the energy of interaction between a solute and solvent molecules. One of the simplest methods to perform solvation analysis is the polarizable continuum model (PCM). This model envisages a solute in a cavity formed by the union of spheres centered on each atom. The procedures provide computation of the electrostatic interaction of the solute, apparent surface charges along with cavitation, dispersion and repulsion contribution¹⁰. Recently, the PCM method has been improved and extended in GAUSSIAN 03.So the cavity can be selected in numerous ways. In this paper, we report the results obtained in the quantum mechanical study of solvation of oxindole derivatives by PCM analysis and correlated free energy solution , its components with the physical properties of solvent.

Method of Computation

The molecular structures are optimized and the optimized structures are solvated with the solvent of various dielectric constants. The physical properties such as dielectric constant, refractive index, and macroscopic surface tension of solvents are listed in Table 1. Computation has been performed with B3LYP method using 6-311++G (d,p) basis set to interpret the solvent effect on the behavior of the solute molecules¹¹. The computer program GAUSSIAN03¹² was used for this purpose. The general structure of four oxindoles and its derivatives used in the present investigation is depicted in Fig.1. In the correlation of free energy solution and electrostatic interaction energy, we used the polarizability which is a function of dielectric constant and these values are calculated using Claussius–Mosotti equation

Table 1: Solvent Descriptors

Solvent	ε	n	γ	α	β
H2O	78.35	1.33	71.99	0.82	0.35
CH3NO2	36.56	1.38	37.48	0.48	0.41
CH3OH	32.63	1.33	22.12	0.43	0.47
C2H5OH	24.85	1.36	31.62	0.37	0.48
ACETONE	20.49	1.36	33.77	0.04	0.49
CH2CL2	8.93	1.37	27.33	0.10	0.05
CHCL3	4.90	1.45	26.53	0.15	0.02
TOLUENE	2.37	1.50	40.20	0	0.14
C6H6	2.27	1.50	40.62	0	0.14
CCL4	2.23	1.46	38.04	0	0

ε – Dielectric Constant at 298˚K.  n- Index of Refraction at optical frequencies at 298˚K.

γ- Macroscopic Surface Tension at a liquid air Interface.   α- Abraham hydrogen bond acidity.

β – Abraham hydrogen bond basicity

Figure 1a:  Molecular Structure of 2-oxindole Click here to View figure

 

Figure 1b: Molecular Structure of 1-Methyl-2-oxindole   Click here to View figure

 

Figure 1c: Molecular Structure of 1-Acetyl-2-oxindole   Click here to View figure

 

Figure 1d:  Molecular Structure of 1-Phenyl-2-Oxindol Click here to View figure

 

F (D) = (D-1/D+2)(M/ ρ)                                                      (1)

where, D = dielectric constant, M = molar mass and ρ =density

Results and Discussion

The possibility of theoretical estimation of solvent effects on the properties of molecules remains a challenge in computational chemistry because the majority of chemically and biologically important reactions occur only in solution. Free energy solution data of pharmaceutically complex solutes in different solvents and solvation analysis are useful for synthetic organic chemists as well as biochemists. It gives them an idea about the solute–solvent interaction and it can be related in the work which builds up a solute in the solvent environment. The solvation effects of oxindole derivatives are investigated using B3LYP with 6-311++G (d, p) basis set. For this purpose the components of free energy solutions such as electrostatic interaction, dispersive energy, repulsive energy, and cavitation energy are computed. These quantities converge quickly during a simulation and thus provide a good assessment of the computational approaches in describing solvent–solute interaction¹³.

Electrostatic interaction energy is due to the dipole–dipole interaction between the solute and solvent molecules. Hence it depends mainly on the dielectric constant of the medium¹¹. The electrostatic energy values are computed in ten solvents and presented in Table 2. It may be pointed out that electrostatic interaction energy values are less in polar solvents and slightly higher in non-polar solvents in the case of all four oxindole compounds. In solvents like water and alcohols there is a possibility of intermolecular hydrogen bonding, which is also a type of strong dipole–dipole interaction. This may be the reason for the high electrostatic interaction of the oxindole derivatives in water and alcoholic solvents. The data in Table 2 suggests that the electrostatic contribution in a given solvent depends on the structure of the solute. Plots of electrostatic energy against dielectric constant of the four systems are depicted in Fig 2.These plots indicate that the electrostatic energy is negative in all the four solutes and solvents investigated. Further, the negative value increases with an increase in dielectric constant of the solvent. Thus, the negative values of electrostatic interaction increases from CCl₄ to water. The present investigation envisages that the electrostatic interaction is more negative in water than other compounds due to hydrophobic effect.

Table 2: Electrostatic energy of Oxindole derivatives in various solvents at 298 K (kJ/mol)

Solvent	2-Oxindole	1- Methyl-	1-Acetyl-	1-Phenyl
		2-Oxindole	2-Oxindole	2-Oxindole
H2O	-46.80	-36.84	-37.30	-42.66
CH3NO2	-22.44	-17.33	-16.95	-18.59
CH3OH	-45.29	-35.54	-35.96	-41.02
C2H5OH	-44.46	-34.83	-35.20	-40.14
ACETONE	-21.60	-16.66	-16.28	-17.83
CH2Cl2	-19.38	-14.94	-14.53	-15.78
CHCl3	-16.41	-12.64	-12.26	-13.19
TOLUENE	-10.63	-8.16	-7.83	-8.33
C6H6	-10.09	-7.74	-7.41	-7.83
CCl4	-9.96	-7.66	-7.33	-7.79

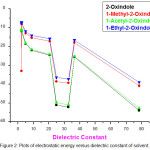Figure 2: Plots of electrostatic energy versus dielectric constant of solvent. Click here to View figure

 

The dispersion energy is due to the polarization of the solute molecules by the solvent molecules. The computed dispersion energy values of the four oxindole derivatives in various solvents are given in Table 3. It is evident from the data presented in Table 3 that there is no significant difference in the dispersion energies in protic solvents of varied dielectric constants. These data also suggest that the dispersion energy is influenced by the polarizability of the solvent which in turn depends upon the size. The plot of dispersive energy against the polarizability function F (D) is presented in Fig 3. The plots of different solutes almost overlap indicating that a structural variation in solute does not influence the dispersion energy. From the table 3 we observe that the dispersive energy is higher in chlorinated solvents than in any other solvents studied here. The same trend has been observed for all the solute molecules. This may be due to the interaction between electronegative atoms in solvent molecules and solute molecules.

Table 3: Dispersive Energy of Oxindole derivatives in various solvents at 298 K (kJ/mol)

Solvent	2-Oxindole	1- Methyl-	1-Acetyl-	1-Phenyl
		2-Oxindole	2-Oxindole	2-Oxindole
H2O	-85.85	-94.06	-101.01	-121.44
CH3NO2	-75.60	-82.80	-82.80	-106.91
CH3OH	-73.63	-80.66	-80.66	-104.15
C2H5OH	-75.18	-82.38	-82.38	-106.32
ACETONE	-68.32	-74.85	-74.85	-96.61
CH2Cl2	-69.70	-76.27	-76.27	-98.54
CHCl3	-62.25	-68.06	-68.06	-87.99
TOLUENE	-83.05	-90.96	-90.96	-117.46
C6H6	-81.29	-89.08	-89.08	-115.03
CCl4	-62.83	-68.69	-68.69	-88.83

 

Figure 3: Plots of dispersive energy versus polarizability function [F(D)]  solvent.  Click here to View figure

 

The repulsive energy between solute and solvent molecules is another important parameter to be considered in solvation analysis. Table 4 shows computed values of repulsive energies of the four solute molecules in ten different media. It is noted that the repulsive energies formed due to solute–solvent interactions had positive values in the solvents. Plots of repulsive energy against refractive index of the solvent of the three solutes are given in Fig 4. From this we observe that the repulsive energy is almost correlated with the refractive index of the solvent except Nitro methane. This may be due to high repulsive negative -ion present in the dichloromethane. By relating the refractive index of the solvent with the repulsive energy it is found that there is a uniform increase in repulsive energy. However, in the case of aromatic solvents, there is an abrupt increase of repulsive energy in all the solutes. Even though ethanol and acetone have same refractive index, there is a variation in the repulsive energies of the oxindole derivatives due to the macroscopic surface tension of the solvent molecules. This might be owing to the fact that both the solute and aromatic hydrocarbon solvents contain π-electrons and a repulsive force between them.

Table 4: Repulsive Energy of Oxindole derivatives in various solvents at 298 K (kJ/mol)

Solvent	2-Oxindole	1- Methyl-	1-Acetyl-	1-Phenyl
		2-Oxindole	2-Oxindole	2-Oxindole
H2O	19.38	20.47	19.76	26.37
CH3NO2	15.78	16.66	16.20	21.47
CH3OH	15.91	16.79	16.24	21.64
C2H5OH	15.99	16.87	16.33	21.77
ACETONE	14.06	14.86	14.36	19.13
CH2Cl2	12.56	13.23	12.98	17.08
CHCl3	10.26	10.80	10.63	13.94
TOLUENE	24.11	25.49	25.49	32.78
C6H6	23.78	25.16	25.16	32.36
CCl4	10.09	10.59	10.59	13.69

 

Figure 4: Plots of repulsion energy versus refractive index of solvent. Click here to View figure

 

The cavitation free energy is a contribution of the solvation free energy. If the cavitation energy is more positive it will reduce the negative value of free energy solution and will influence the solubility. The values of cavitation energy are computed for the four oxindole compounds in different solvents at 298 K by B3LYP method with 6-311++G (d, p) basis set and listed in Table 5. It can be seen that cavitation energy is positive for the four solutes in all the ten solvents at 298 K. Analysis of cavitation energy data in Table 5 reveals that the cavitation energy correlated with macroscopic surface tension depends on the structure of solute, nature of solvent and macroscopic surface tension of solvent. Fig.5 shows plots of cavitation energy graph versus surface tension graph.

Table 5: Cavitation energy of Oxindole derivatives in various solvents at 298 K (kJ/mol)

Solvent	2-Oxindole	1- Methyl-	1-Acetyl-	1-Phenyl
		2-Oxindole	2-Oxindole	2-Oxindole
H2O	73.51	82.00	93.18	109.42
CH3NO2	63.08	70.32	79.95	93.81
CH3OH	53.29	59.40	67.52	79.20
C2H5OH	54.33	60.57	68.86	80.79
ACETONE	52.28	58.27	66.22	77.69
CH2Cl2	54.59	60.82	69.15	81.12
CHCl3	53.04	59.06	67.15	78.78
TOLUENE	58.85	65.51	74.51	87.40
C6H6	59.82	66.64	75.77	88.87
CCl4	55.05	61.28	69.7	81.75

 

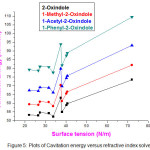Figure 5: Plots of Cavitation energy versus refractive index solvent. Click here to View figure

 

The molecular free energy in solution can be written as a sum of four contributions.

ΔG_solv = ΔG_ele+ΔG_disp+ΔG_rep+ΔG_cav                                    (2)

Where ΔG_ele is the electrostatic contribution, ΔG_cav is a positive term corresponding to the work spent in forming a suitable cavity in the medium. ΔG_disp is the dispersion contribution due to the coupling work and ΔG_rep is a repulsion term due to the non covalent interactions. ΔG_cav is the work needed to form the cavity. The dispersion-repulsion terms are calculated adopting the atom-atom potential parameters proposed by Caillet and Claverie [17-19].  Table 6 shows how the different characteristic of each solvent affects the free energy salvation of the four selected molecules. For example benzene & toluene have similar refractive index but benzene has high favorable free energy solvation than toluene because of increased favorable electrostatic interactions. For solvents CH₂Cl₂ & CHCl₃ the refractive index is lower than benzene refractive index. In addition to hydrogen bond basicity parameter, benzene provides high favorable free energy solvation due to higher macroscopic surface tension and its basicity parameter. From the study we observe that the free energy solvation of all the four molecules of water is comparatively less favourable than that of the other solvents because of the hydrophobic effect. But Table 6 shows that the free energy solvation in methanol & ethanol are least favorable out of all the solvents listed. And this favorable interaction is outweighted by the hydrophobic contribution. The present study of the solute-solvent interaction is mainly due to dipole-dipole attraction. In order to express the solute-solvent interaction, the dipole moment and Induced dipole moment values are calculated and listed in Table 7 & 8. The Induced dipole moment of a given solute slightly increases with dielectric constant of the solvent. The induced dipole moment with the dielectric constant of the solvent in Fig.6 shows plots of Induced dipole moment against dielectric constant of the solvent. Polar solvents have large dipole moments and contain bonds between atoms with very different electro negativities, such as oxygen and hydrogen.

Table 6: Free energy of Oxindole derivatives in various solvents at 298 K (kJ/mol)

Solvent	2-Oxindole	1- Methyl-	1-Acetyl-	1-Phenyl
		2-Oxindole	2-Oxindole	2-Oxindole
H2O	-39.77	-28.38	-25.33	-28.3
CH3NO2	-19.13	-13.10	-9.84	-10.21
CH3OH	-49.73	-40.02	-38.89	-44.29
C2H5OH	-49.31	-39.73	-38.55	-43.95
ACETONE	-23.57	-18.38	-16.07	-17.62
CH2Cl2	-21.89	-17.12	-14.61	-16.12
CHCl3	-15.36	-10.84	-7.91	-8.50
TOLUENE	-10.72	-8.12	-6.11	-5.61
C6H6	-7.79	-5.02	-2.76	-1.63
CCl4	-7.66	-4.44	-1.30	-1.13

Table 7: Dipole moment of the oxindole derivatives in Debyes

Compound Name	Dipole moment Value
2-Oxindole	3.1379
1-Methyl-2-Oxindole	2.8790
1-Acetyl-2-Oxindole	2.5566
1-Phenyl-2-Oxindole	3.0600

 

Table 8: Induced dipole moment of Oxindole derivatives in various solvents at 298 K (kJ/mol)

Solvent	2-Oxindole	1- Methyl-	1-Acetyl-	1-Phenyl
		2-Oxindole	2-Oxindole	2-Oxindole
H2O	3.82	3.67	3.75	4.49
CH3NO2	3.70	3.50	3.36	4.07
CH3OH	3.80	3.65	3.71	4.44
C2H5OH	3.80	3.63	3.69	4.41
ACETONE	3.68	3.48	3.33	4.03
CH2Cl2	3.63	3.42	3.24	3.93
CHCl3	3.57	3.34	3.13	3.79
TOLUENE	3.43	3.18	2.92	3.53
C6H6	3.41	3.16	2.90	3.50
CCl4	3.41	3.16	2.90	3.50

 

Figure 6: Plots of Induced dipole moment versus dielectric constant solvent. Click here to View figure

 

Conclusion

We have adopted a reliable self consistent field method, which combines a Polarizable Continuum Model of the solvent with DFT for the solute to calculate the solvation free energy and its component in various solvents. The electrostatic interaction contribution of the free energy can be satisfactorily correlated with the dielectric constant of the solvent. Although their dielectric constants are small, the dispersive energy is high for the four solutes in CCl₄ among organic solvents. The correlation between repulsive energy and refractive index of the solvent is fairly satisfactory. ΔG_solv values of the four solutes in different media are computed by summing up the component energies. The values of the free energy solution of the four solutes in all the ten solvents are negative. It suggests that the dissolution process is thermodynamically feasible for the four solutes in the investigated solvents. The induced dipole moments are high in polar solvents and for a given solute it is highest in water and lowest in CCl₄.

References

1. Chevan,  P.; Mane, A.S.; Shingare, M.S.; Indian J. Chem. 2001, 408, 339.
2. Zhou, F.; Liu,Y.L.; Zhou, J. Adv. Synth. Catal. 2010, 352, 1381–1407.
   CrossRef
3. Huters, A.D.;  Styduhar, E.D.;  Garg, Angew. N.K.;  Chem. Int. Ed.  2012, 51,3758–3765.
   CrossRef
4. Ball-Jones, N.R.; Badillo, J.J.; Franz, A.K.; Org. Biomol. Chem. 2012, 10, 5165–5181.
   CrossRef
5. Dalpozzo, R.;  Bartoli, G.;  Bencivenni, G.;  Chem. Soc. Rev. 2012, 41, 7247–7290.
   CrossRef
6. Jursic, B.; Stevens, E.D.; Tetrahedron Lett.2002, 43, 5681—5683.
   CrossRef
7. Azizian, J.; Mohammadi, A.A.; Karimi, N.; Mohammadizade,  M.R.; Karimi, A.R.; Catal.Commun. 2006,  7, 752—755.
   CrossRef
8. Wang, S.Y.;  JiS. J., Tetrahedron, 2006, 62, 1527—1535.
   CrossRef
9. Yadav, J. S.; Reddy, B.V.S.; Gayathri, K.U., Meraj, S.; Prasad,  A.R.; Synthesis, 2006, 4.,121—4123.
10. Sathyanarayanamoorthi, V.; Sukumaran, K.; Kannappan, V.; Brindha, S.; J. Mol. Liq. 2011, 160, 125–129.
    CrossRef
11. Winget, P.; Thompson, J.D.; Cramer, C.J.; Truhlar, D.G.; J. Phys. Chem.2002, 106 5160–5168.
12. Frisch, M.J.;  Trucks, G.W.; Schlegel, H.B.;  Scuseria, G.E.;   Robb, M.A.;  J.R. Cheeseman, J.R.; Montgomery J.A.; Vreven, T.; Kudin, K.N.;  Burant, J.C.;  Millam, J.M.;  Iyengar, S.S. ; Tomasi, J.; Barone, V.;  Mennucci, B.;  Cossi, M.;  Scalmani, G.; Rega, N.; Petersson, G.A. ; Nakatsuji, H.; Hada, M.; Ehara, M.; Toyota, K.; Fukuda, R.; Hasegawa, J.; Ishida, M.; Nakajima, T.; Honda, Y.;  Kitao, O.;  Nakai, H.;  Klene, M.;  Li, X.; Knox, J.E.; Hratchian, H.P.; Cross, J.B.; Adamo, C.; Jaramillo, J.; Gomperts, R.; Stratmann, R.E.; Yazyev, O. ; Austin, A.J.; Cammi, R. Pomelli, C.;  Ochterski, J.W.; Ayala, P.Y.; Morokuma, K..; Voth, G.A. .; Salvador, P.;  Dannenberg, J.J.;  Zakrzewski, V.G.; Dapprich, S.; Daniels, A.D.;  Strain, M.C.; Farkas, O.; Malick, D.K.;  Rabuck, A.D.; Raghavachari, K.;  Foresman,  J.B.; Ortiz, J.V.; Cui, Q.;  Baboul, A.G.; Clifford, S.;  Cioslowski, J.;  Stefanov, B.B.; Liu, G.;  Liashenko, A.; Piskorz, I.; Komaromi, R.L.; Martin, D.J.; Fox, T.; Keith, M.A.; Al-Laham, C.Y. Peng, Nanayakkara, A.;  Challacombe, M.; Gill, P.M.W.; Johnson, B.; Chen, W.; Wong,M.W.; Gonzalez,  C.; Pople, J.A.;Gaussian 03, Revision B.01, Gaussian, Inc., 2003.
13. Elena Cuhero, F.;  Javier Lugne, Modesto Orozco, JialiGao, J. Phys. Chem.,     2003, B107, 1664–1671.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.