Study of Correlation Between the Atomic Numbers and the Atomic Weights of Elements in the Periodic Table With Sierpinski Triangle Fractals
Leila Hojatkashani
Department of Chemistry, College of Basic Sciences, Yadegar-e-Imam Khomeini (RAH) Branch, Islamic Azad University. Tehran. Iran.
DOI : http://dx.doi.org/10.13005/ojc/330247
Article Received on : February 02, 2017
Article Accepted on : April 09, 2017
Waclaw Sierpinski described fractal geometries such as Sierpinski triangle, gasket and carpet. In this paper, Sierpinski triangle is used to find any equation between the atomic number and the atomic weight of elements in the periodic table. First by using Matlab program, an algorithm is written to create a right angle triangle between the atomic numbers and atomic weights. Then this original triangle is divide to 8 smaller triangles on the hypotenuse of the original triangle to get more accurate results and reduce errors. Finally, equations of correlation between the atomic numbers and the atomic weights of elements are obtained to calculate the atomic weights of the elements in eighth period.
KEYWORDS:Sierpinski’s fractals; self-similarity; the periodic table of the elements; atomic number; atomic weight; right angled triangle; Matlab program
Download this article as:| Copy the following to cite this article: Hojatkashani L. Study of Correlation Between the Atomic Numbers and the Atomic Weights of Elements in the Periodic Table With Sierpinski Triangle Fractals. Orient J Chem 2017;33(2). |
| Copy the following to cite this URL: Hojatkashani L. Study of Correlation Between the Atomic Numbers and the Atomic Weights of Elements in the Periodic Table With Sierpinski Triangle Fractals. Orient J Chem 2017;33(2). Available from: http://www.orientjchem.org/?p=31207 |
Introduction
In 1975 Benoit Mandelbrot introduced a new branch of geometry known as fractal geometry to find order in chaotic shapes. In fact, fractal geometries describe the fractals which have complex geometric structures in natural and physical sciences. Most of fractal objects are self-similar in nature which means that if a tiny portion of a geometric structure is enlarged, an analogous structure of the whole is obtained. This means that the fractal objects could be broken into even finer pieces having same features as the original and with dimension always less than its original. The dimension of a fractal object is usually not an integer but fractional. Fractal objects are omnipresent in nature and can be well-approximated mathematically. There are some mathematically developed fractals such as Cantor set by George Cantor, Peano’s curve by Giuseppe Peano, Koch’s curve by Helge von Koch in, Sierpinski’s fractals such as carpet, triangle, etc., by Waclaw Sierpinski in, Julia set by Gaston Julia [1].
The triangle known as Sierpinski triangle can be considered as the composition of three small equal triangles, each of them is exactly half the size and of the self-similar copies original triangle. Thus if we magnify any of these three triangles by a factor of 2, we will get the original triangle. Again, each of these three small self-similar triangles can be considered as the combination of another three small self-similar triangles. This type of self-similarity is known as exact self-similarity. It is the strongest self-similarity occurred in fractal images [1]. The Sierpinski triangle is a canonical starting point for many researches for fractals and self-assembly. Winfree showed that the Sierpinski triangle weakly self-assembles [2].
Sierpinski gasket and carpet were discovered by the Polish mathematician Waclaw
Sierpinski in 1916 .Imagine filled equilateral triangle such as S0 with each side of unit length. Now divide this triangle into four equal small equilateral triangles using the midpoints of the
three vertices of the original triangle S0 as new vertices and remove the interior of the middle triangle. The result is a triangle called S1. Repeat this process in each of the remaining three equal triangles to produce the triangle S2. Repeat this process continuously and finally the Sierpinski triangle is formed. The figure1 displays five steps of Sierpinski triangle. [1].
![Figure 1: Construction of Sierpinski triangle [1]](http://www.orientjchem.org/wp-content/uploads/2017/04/Vol33No2_Stud_Leil_fig1-150x150.jpg) |
.[Figure 1: Construction of Sierpinski triangle [1
|
We start by labeling p1, p2 and p3 as the corners of the Sierpinski triangle, and a random point v1. Set vn+1 = ½ ( vn + pr n ), where rn is a random number 1, 2 or 3. If the first point v1 was a point on the Sierpiński triangle, then all the points vn lie on the Sierpinski triangle. If the first point v1 to lie within the perimeter of the triangle is not a point on the Sierpinski triangle, none of the points vn will lie on the Sierpinski triangle, however they will converge on the triangle. If v1 is outside the triangle, the only way vn will land on the triangle, is the triangle was infinitely large. The algorithm can be applied to any kind of triangle. Also, the same rule can be applied to other objects like pyramids, cubes, etc. The above algorithm is not the only method to draw a Sierpinski triangle. There is a method called iterated function systems (IFS) [3]. The number of triangles in a Sierpinski triangle can be found by using the formula Nn=3n, where N is the number of triangles and n the number of iterations [4].
In this research we uase righ-angled Sierpinski triangled which can be called as disceret Sierpinski triangle. To draw this triangle, first we drew a triangle with vertices (0, 0), (1, 0), and (0, 1). Then it will be devided to a smaller triangle with vertices (3/4, 3/4), (1, 3/4), and (3/4, 1).Then three smaller triangles, one with vertices (3/8, 3/8),(1/2, 3/8), (3/8, 1/2), one with (7/8, 3/8), (1, 3/8), (7/8, 1/2), and one with vertices (3/8, 7/8), (1/2,7/8), (3/8, 1) [4]. The whole shape can be seen as it is made of three pieces scaled by 1/2 and one piece scaled by 1/4. The result suggests defining a process: replace a shape by three copies scaled by 1/2 and one copy scaled by 1/4. Taking the base and altitude of the fractal to be 1, the process consists of four transformations as functions below and figure 2 [5].
T1(x, y) = (x/2, y/2) T2(x, y) = (x/2, y/2) + (1/2, 0)
T3(x, y) = (x/2, y/2) + (0, 1/2) T4(x, y) = (x/4, y/4) + (3/4, 3/4). [5]
![Figure 2: Construction of righ-angled Sierpinski triangle [5] [6]](http://www.orientjchem.org/wp-content/uploads/2017/04/Vol33No2_Stud_Leil_fig21-150x150.jpg) |
Figure 2: Construction of righ-angled Sierpinski triangle [5] [6] |
The periodic table of elements was create by Russian scientist Dmitri Ivanovich Mendeleev . In this research, we try to perform Sierpinski triangled algorithm on this table in which the chemical elements are arranged by order of atomic number in such a way that the periodic properties (chemical periodicity) of the elements are made clear. In this research, we used righ-angled Sierpinski triangled in order to find the corrolation between atomic number and atomic weight of 118 elements in the periodic table.
Computional Method
This method provides the graphical analysis of the behaviour between atomic number and atomic weight , so MATLAB 2013 software is used for writing the right angle triangle algorithm and analyzing graphically the corrolation between atomic number and atomic weight. In th first step, by using the software , we drew a triangle with vertices as below:
px(1)=0;
px(2)=120;
px(3)=120;
py(1)=0;
py(2)=0;
py(3)=310;
vx_in=60;
vy_in=145;
In the next step, we divide the triangle into smaller triangles as seven period of the periodic table to get more accuracy in results. Each triangle are different in vertices , vx and Vy. In each step we study the hypotenuse of the triangles to determine the relationship between atomic number and atomic weight of 118 elements and more accurate results.
Results and Discussion
The Initial Triangle
The main purpose in this study is determination of the atomic weight of elements by their atomic nomber with a righ-angle Sierpinski triangle algorithm. To achieve this goal, we used Matlab 2013 software to write the triangle algorithm with vertices , vx and vy as blow:
px(1)=0;
px(2)=120;
px(3)=120;
py(1)=0;
py(2)=0;
py(3)=310;
vx_in=60;
vy_in=155;
By running the progrom, the results are shown as figure(3) which the atomic number of elements are as axis (X).The origin right angled triangle is divided to other triangles and showed by white color triangles which in these triangles, there are no points. On the contrary, the blue parts are consisted of points. Each point shows an atomic number and atomic weight. The weights of elements which are resulted by Sierpinski algorithm are near and along the hypotenuse of the original triangle. Some of the atomic weights are resulted in white triangles and because there are no points in them, they cannot be accepted and are shown with red points . So the program has chosen the nearest point for those atomic weight in blue parts. The atomic weights which are chosen by the program can be seen with green points in figure (3).
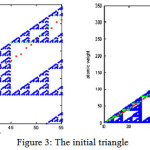 |
Figure 3: The initial triangle
|
The results of the Sierpinski algorithm are shown in table (1) which atomic symbols, atomic Numbers, atomic weights of the periodic table and also calculated atomic numbers and atomic weights by Sierpinski right angled triangle algorithm are demonstrated. As it is shown in the table (1) the calculated atomic numbers and atomic weights are not exactly same as atomic numbers and atomic weights in the periodic table and there are more or less errors in them. Also, table (1) shows that for some of elements, calculated atomic weights are the same beacause the atomic weights of those elements have resulted in the white triangles which there are no points. So the program had to choose the same number for their weights in blue parts of the the initial triangle, where there are points and numbers.
Calculation in the blue parts is the main reason of occuring error in atomic Numbers and atomic weights which are resulted by Sierpinski right angled triangle algorithm. The percentage of absolute errors in obtained atomic Numbers and atomic weights are demonstrated in table (2). In table (2), Helium, Lithium, Beryllium, Boron, Carbon, Fluorine, Neon, Magnesium ,Aluminum and silicon have the highest percentage of absolute errors in obtained atomic number while Helium, Beryllium, Oxygen, Magnesium, Aluminum, Phosphorus, Sulfur, chlorine, Vanadium, Chromium, Manganese, Iron, Zinc, Gallium, Germanium, Strontium, Yttrium, Zirconium, Rhodium, Palladium , Silver, Neodymium and Promethium have the highest percentage of absolute errors in obtained atomic weights.
Table 1: Atomic Symbol, Atomic Number, Atomic Weight , Calculated Atomic Number and Calculated Atomic Weight by initial Sierpinski right angled triangle algorithm
| Atomic Symbol | Atomic Number | Atomic Weight | Calculated Atomic Number | Calculated Atomic Weight | Atomic Symbol | Atomic Number | Atomic Weight | Calculated Atomic Number | Calculated Atomic Weight |
| H | 1 | 1.00794 | 1 | 1 | Rh | 45 | 102.906 | 45 | 116.25 |
| He | 2 | 4.0026 | 2.1094 | 5.44922 | Pd | 46 | 106.421 | 46.1719 | 116.8555 |
| Li | 3 | 6.941 | 2.5781 | 6.66016 | Ag | 47 | 107.868 | 47.1094 | 116.8555 |
| Be | 4 | 9.01218 | 3.75 | 9.6875 | Cd | 48 | 112.411 | 48.0469 | 116.8555 |
| B | 5 | 10.811 | 5.1562 | 10.8984 | In | 49 | 114.818 | 48.9844 | 116.8555 |
| C | 6 | 12.0107 | 6.3281 | 11.5039 | Sn | 50 | 118.71 | 49.6875 | 118.6719 |
| N | 7 | 14.0067 | 7.0312 | 13.3203 | Sb | 51 | 121.76 | 50.8594 | 121.6992 |
| O | 8 | 15.9994 | 7.5 | 19.375 | Te | 52 | 127.603 | 52.2656 | 127.7539 |
| F | 9 | 18.9984 | 8.6719 | 19.9805 | I | 53 | 126.904 | 53.4375 | 118.6719 |
| Ne | 10 | 20.1797 | 9.6094 | 19.9805 | Xe | 54 | 131.293 | 53.6719 | 136.2305 |
| Na | 11 | 22.9898 | 11.0156 | 22.4023 | Cs | 55 | 132.905 | 54.6094 | 136.2305 |
| Mg | 12 | 24.305 | 12.4219 | 29.668 | Ba | 56 | 137.327 | 56.0156 | 137.4414 |
| Al | 13 | 26.9815 | 13.3594 | 24.8242 | La | 57 | 138.905 | 57.4219 | 138.6523 |
| Si | 14 | 28.0855 | 14.2969 | 27.2461 | Ce | 58 | 140.116 | 58.125 | 140.4688 |
| P | 15 | 30.9738 | 15 | 38.75 | Pr | 59 | 140.908 | 59.2969 | 141.0742 |
| S | 16 | 32.065 | 16.1719 | 39.3555 | Nd | 60 | 144.242 | 60.2344 | 155.6055 |
| Cl | 17 | 35.453 | 17.1094 | 39.3555 | Pm | 61 | 145 | 61.1719 | 155.6055 |
| Ar | 18 | 39.948 | 18.2812 | 39.9609 | Sm | 62 | 150.362 | 62.1094 | 155.6055 |
| K | 19 | 39.0983 | 18.9844 | 39.3555 | Eu | 63 | 151.964 | 63.0469 | 155.6055 |
| Ca | 20 | 40.078 | 20.1562 | 39.9609 | Gd | 64 | 157.253 | 64.4531 | 156.8164 |
| Sc | 21 | 44.9559 | 21.0937 | 44.8047 | Tb | 65 | 158.925 | 65.1562 | 158.6328 |
| Ti | 22 | 47.867 | 22.0312 | 47.2266 | Dy | 66 | 162.5 | 66.3281 | 161.6602 |
| V | 23 | 50.9415 | 22.5 | 58.125 | Ho | 67 | 164.93 | 66.7969 | 165.293 |
| Cr | 24 | 51.9961 | 23.6719 | 58.7305 | Er | 68 | 167.259 | 67.5 | 174.375 |
| Mn | 25 | 54.938 | 24.6094 | 58.7305 | Tm | 69 | 168.934 | 69 | 164.6875 |
| Fe | 26 | 55.845 | 26.4844 | 58.7305 | Yb | 70 | 173.054 | 69.6094 | 174.9805 |
| Co | 27 | 58.9332 | 27.4219 | 58.7305 | Lu | 71 | 174.967 | 71.4844 | 174.9805 |
| Ni | 28 | 58.6934 | 28.3594 | 58.7305 | Hf | 72 | 178.492 | 72.4219 | 177.4023 |
| Cu | 29 | 63.546 | 29.2969 | 63.5742 | Ta | 73 | 180.948 | 73.3594 | 179.8242 |
| Zn | 30 | 65.382 | 30.2344 | 78.1055 | W | 74 | 183.841 | 74.2969 | 184.668 |
| Ga | 31 | 69.723 | 31.1719 | 78.1055 | Re | 75 | 186.207 | 75 | 193.75 |
| Ge | 32 | 72.641 | 32.1094 | 78.1055 | Os | 76 | 190.233 | 76.1719 | 194.3555 |
| As | 33 | 74.9216 | 33.0469 | 78.1055 | Ir | 77 | 192.217 | 77.1094 | 194.3555 |
| Se | 34 | 78.963 | 34.2187 | 78.7109 | Pt | 78 | 195.084 | 78.2812 | 194.9609 |
| Br | 35 | 79.904 | 34.6875 | 79.9219 | Au | 79 | 196.967 | 78.5156 | 196.7773 |
| Kr | 36 | 83.798 | 36.0937 | 83.5547 | Hg | 80 | 200.592 | 80.1562 | 197.3828 |
| Rb | 37 | 85.4678 | 36.7969 | 85.3711 | Tl | 81 | 204.383 | 81.0937 | 204.6484 |
| Sr | 38 | 87.621 | 38.4375 | 79.9219 | Pb | 82 | 207.21 | 82.0312 | 207.0703 |
| Y | 39 | 88.9059 | 39.375 | 82.3437 | Bi | 83 | 208.98 | 82.5 | 213.125 |
| Zr | 40 | 91.224 | 39.6094 | 97.4805 | Po | 84 | 209 | 83.6719 | 213.7305 |
| Nb | 41 | 92.9064 | 41.4844 | 97.4805 | At | 85 | 210 | 84.6094 | 213.7305 |
| Mo | 42 | 95.962 | 42.4219 | 97.4805 | Rn | 86 | 222 | 85.7812 | 221.6016 |
| Tc | 43 | 98 | 42.6562 | 98.0859 | Fr | 87 | 223 | 87.4219 | 223.418 |
| Ru | 44 | 101.072 | 44.2969 | 99.9023 | Ra | 88 | 226 | 87.8906 | 225.8398 |
| Atomic Symbol | Atomic Number | Atomic Weight | Calculated Atomic Number | Calculated Atomic Weight | Atomic Symbol | Atomic Number | Atomic Weight | Calculated Atomic Number | Calculated Atomic Weight |
| Ac | 89 | 227 | 89.2969 | 225.8398 | Rf | 104 | 267 | 104.2969 | 267.0117 |
| Th | 90 | 232.038 | 90 | 232.5 | Db | 105 | 268 | 105 | 271.25 |
| Pa | 91 | 231.036 | 91.1719 | 233.1055 | Sg | 106 | 271 | 106.1719 | 271.8555 |
| U | 92 | 238.029 | 92.1094 | 237.9492 | Bh | 107 | 272 | 107.1094 | 271.8555 |
| Np | 93 | 237 | 93.2812 | 236.1328 | Hs | 108 | 270 | 108.0469 | 271.8555 |
| Pu | 94 | 244 | 94.4531 | 244.0039 | Mt | 109 | 276 | 108.5156 | 276.6992 |
| Am | 95 | 243 | 94.9219 | 242.793 | Ds | 110 | 281 | 109.9219 | 281.543 |
| Cm | 96 | 247 | 95.625 | 247.0313 | Rg | 111 | 280 | 110.8594 | 281.543 |
| Bk | 97 | 247 | 96.7969 | 247.6367 | Cn | 112 | 285 | 112.0313 | 284.5703 |
| Cf | 98 | 251 | 97.5 | 251.875 | Nh | 113 | 284 | 112.5 | 290.625 |
| Es | 99 | 252 | 98.6719 | 252.4805 | Fl | 114 | 289 | 113.6719 | 291.2305 |
| Fm | 100 | 257 | 99.6094 | 257.3242 | Mc | 115 | 288 | 114.6094 | 291.2305 |
| Md | 101 | 258 | 101.0156 | 258.5352 | Lv | 116 | 293 | 116.0156 | 292.4414 |
| No | 102 | 259 | 102 | 261.5625 | Ts | 117 | 294 | 117.2 | 293 |
| Lr | 103 | 262 | 103.3594 | 262.168 | Og | 118 | 294 | 118.125 | 295.4688 |
The interesting point is that smaller and lighter elements have the highest errors but heavier elements have shown much less errors in results. In this method, the average of %error for the calculated Atomic Numbers is %0.898 and the average of %error for the calculated Atomic weights is %3.4568.
The Seven Period Triangles
There are seven period in the periodic table of elements. In this step, for each period of the periodic table, we create a triangle exept for the seventh period which we make two triangles. For this purpose, the Sierpinski right angled triangle algorithm is slightly changed, so the hypotenuse of the original triangle are divide to 8 right angled triangle. Table 3 shows the changes with vertices, vx and Vy to make 8 triangles out of the origin one. This process is done to see the effect of dividing the original on accuracy of calculated atomic number and atomic weight of elements and %errors for both these factors.
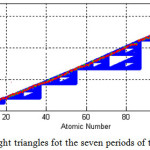 |
Figure 4: The eight triangles fot the seven periods of the periodic table Click here to View figure |
Table 2: %Error in calculated Atomic Number and calculated Atomic Weight by initial Sierpinski right angled triangle algorithm
| Atomic Symbol | % Error in Atomic | % Error in Atomic | Atomic Symbol | % Error in Atomic | Atomic Symbol | % Error in Atomic | ||
| Number | Weight | % Error in Atomic | Weight | Number | % Error in Atomic | |||
| Number | Weight | |||||||
| H | 0 | 0.79 | Nb | 1.1814 | 4.9233 | Tl | 0.1157 | 0.1297 |
| He | 5.47 | 36.1419 | Mo | 1.0045 | 1.5824 | Pb | 0.0381 | 0.0674 |
| Li | 14.0625 | 4.0462 | Tc | 0.7994 | 0.0876 | Bi | 0.6024 | 1.9832 |
| Be | 6.25 | 7.4934 | Ru | 0.7647 | 1.1572 | Po | 0.3906 | 2.2634 |
| B | 3.125 | 0.8088 | Rh | 0 | 12.9677 | At | 0.4595 | 1.7764 |
| C | 5.4687 | 4.2195 | Pd | 0.3736 | 9.8049 | Rn | 0.2544 | 0.1794 |
| N | 0.4464 | 4.9004 | Ag | 0.2327 | 8.3317 | Fr | 0.4849 | 0.1874 |
| O | 6.25 | 21.0982 | Cd | 0.0976 | 3.9537 | Ra | 0.1243 | 0.0709 |
| F | 3.6458 | 5.1692 | In | 0.0319 | 1.7745 | Ac | 0.3336 | 0.5111 |
| Ne | 3.9062 | 0.9872 | Sn | 0.625 | 0.0321 | Th | 0 | 0.1991 |
| Na | 0.1421 | 2.553 | Sb | 0.2757 | 0.0499 | Pa | 0.1888 | 0.8958 |
| Mg | 3.5156 | 22.0653 | Te | 0.5108 | 0.1182 | U | 0.1189 | 0.0335 |
| Al | 2.7644 | 7.9955 | I | 0.8255 | 6.4872 | Np | 0.3024 | 0.3659 |
| Si | 2.1205 | 2.9887 | Xe | 0.6076 | 3.6707 | Pu | 0.482 | 0.0016 |
| P | 0 | 25.1058 | Cs | 0.7102 | 2.5018 | Am | 0.0822 | 0.0852 |
| S | 1.0742 | 22.7365 | Ba | 0.0279 | 0.0833 | Cm | 0.3906 | 0.0127 |
| Cl | 0.6434 | 11.0074 | La | 0.7401 | 0.1822 | Bk | 0.2094 | 0.2577 |
| Ar | 1.5625 | `0.0323 | Ce | 0.2155 | 0.2518 | Cf | 0.5102 | 0.3486 |
| K | 0.0822 | 0.6577 | Pr | 0.5032 | 0.1182 | Es | 0.3314 | 0.1907 |
| Ca | 0.7812 | 0.2921 | Nd | 0.3906 | 7.8781 | Fm | 0.3906 | 0.1261 |
| Sc | 0.4464 | 0.3364 | Pm | 0.2818 | 7.3141 | Md | 0.0154 | 0.2074 |
| Ti | 0.142 | 1.3379 | Sm | 0.1764 | 3.4872 | No | 0 | 0.9894 |
| V | 2.1739 | 14.1015 | Eu | 0.0744 | 2.3963 | Lr | 0.3489 | 0.0641 |
| Cr | 1.3671 | 12.9517 | Gd | 0.708 | 0.2776 | Rf | 0.2855 | 0.0044 |
| Mn | 1.5625 | 6.9031 | Tb | 0.2403 | 0.1841 | Db | 0 | 1.2127 |
| Fe | 1.863 | 5.1669 | Dy | 0.4972 | 0.5168 | Sg | 0.1621 | 0.3157 |
| Co | 1.5625 | 0.3439 | Ho | 0.3032 | 0.2199 | Bh | 0.1025 | 0.0531 |
| Ni | 1.2835 | 0.0631 | Er | 0.7353 | 4.2544 | Hs | 0.0434 | 0.6872 |
| Cu | 1.0237 | 0.0444 | Tm | 0 | 2.5138 | Mt | 0.4444 | 0.2533 |
| Zn | 0.7813 | 19.4602 | Yb | 0.558 | 1.1132 | Ds | 0.071 | 0.1932 |
| Ga | 0.5544 | 12.0225 | Lu | 0.6822 | 0.0078 | Rg | 0.1266 | 0.5511 |
| Ge | 0.3418 | 7.5225 | Hf | 0.5859 | 0.6105 | Cn | 0.0279 | 0.1508 |
| As | 0.1421 | 4.2496 | Ta | 0.4923 | 0.6209 | Nh | 0.4424 | 2.3327 |
| Se | 0.6434 | 0.3192 | W | 0.4012 | 0.4498 | Fl | 0.2878 | 0.7718 |
| Br | 0.8928 | 0.0224 | Re | 0 | 4.0509 | Mc | 0.3396 | 1.1217 |
| Kr | 0.2604 | 0.2903 | Os | 0.2261 | 2.1671 | Lv | 0.0134 | 0.1906 |
| Rb | 0.5489 | 0.1131 | Ir | 0.142 | 1.1125 | Ts | 0.1709 | 0.3401 |
| Sr | 1.1513 | 8.7868 | Pt | 0.3606 | 0.0631 | Og | 0.1059 | 0.4996 |
| Y | 0.9615 | 7.3809 | Au | 0.6131 | 0.0961 | |||
| Zr | 0.9765 | 6.8583 | Hg | 0.1953 | 1.5999 |
Table 3: Vertices , vx and vy of triangles for the seven period
|
first Period |
Second Period |
Third Period |
Fourth Period |
|
px(1)=0; px(2)=3; |
px(1)=3; |
px(1)=11; |
px(1)=19; |
|
px(3)=3; |
px(2)=11; |
px(2)=19; |
px(2)=37; |
|
py(1)=0; |
px(3)=11; |
px(3)=19; |
px(3)=37; |
|
py(2)=0; |
py(1)=6.5; |
py(1)=23; |
py(1)=39; |
|
py(3)=6; |
py(2)=6.5; |
py(2)=23; |
py(2)=39; |
|
vx_in=1.6 |
py(3)=23; |
py(3)=39.95; |
py(3)=85.47; |
|
vy_in=2.9 |
vx_in=7; |
vx_in=16; |
vx_in=28; |
|
vy_in=13; |
vy_in=32; |
vy_in=62 |
|
|
Fifth Period |
Sixth Period |
Seventh Period(a) |
Seventh Period(b) |
|
px(1)=37; |
px(1)=55; |
px(1)=87; |
px(1)=104; |
|
px(2)=55; |
px(2)=87; |
px(2)=105; |
px(2)=118; |
|
px(3)=55; |
px(3)=87; |
px(3)=105; |
px(3)=118; |
|
py(1)=85.47; |
py(1)=132.9; |
py(1)=223; |
py(1)=267; |
|
py(2)=85.47; |
py(2)=132.9; |
py(2)=223; |
py(2)=267; |
|
py(3)=132.9; |
py(3)=223; |
py(3)=267; |
py(3)=294; |
|
vx_in=48; |
vx_in=79; |
vx_in=100; |
vx_in=114; |
|
vy_in=112.4 |
vy_in=197; |
vy_in=257; |
vy_in=289; |
The Calculated atomic numbers and atomic weights resulted by eight right-angle Sierpinski triangles algorithm are shown in table 4. Comparing this table with table 1, shows that the numbers specially calculated atomic weights are more acurrate and closer to real ones. Also, there are less elements with same atomic weights in this method the groups with such condition have shifted to heavier elements. Figure 4 shows the triangles for the seven period, which there are six triangles for the periods 1-6 and two triangles for the period 7 which it is done to see better results in the last period. The atomic weights of 118 elements are shown as red points. As it is seen, the hypotenuse of the connected triangles is not a stright line, that it is a curve.
Also with comparing tables 2 and 5, we see that %error for some elements such as Helium, Lithium, Oxygen, Fluorine, Magnesium, Aluminium, Silicon, Chlorine, Vanadium, Argon , Chromium, manganese, Iron, Zinc, Galium, Germanium, Rhodium, Paladium and Silver %errors in Atomic weight and atomic number are reduced. For Some elemnts such as Nitrogen, Nickel, Selenium, Barium and Gold, there are increased %errors in their atomic numbers or atomic weights. However, In this method, the average of %errors for the calculated atomic Numbers and the calculated atomic weights, respectively, are reduced to %0.6867 and %0.4113. This means that dividing the hypotenuse of the initial triangle to eight triangles was a successful method to reduce %errors in resulted numbers.
Comparing the Equations
In this level,by using Excel- 2016 program and the numbers in tables 1 and 4, we try to drew two plots and achieve their equations. In the first plot, the atomic numbers and the atomic weights in the periodic table of elements are used , respectively, as axis X and Y. The best resulted equation between these two parameter is a third degree equation (eq.1). The curve is shown in figure(5).
Table 4: Atomic Symbol, Atomic Number, Atomic Weight , calculated Atomic Number and calculated Atomic Weight by eight Sierpinski right angled triangles algorithm
|
Atomic Symbol |
Atomic Number |
Atomic Weight |
Calculated Atomic Number |
Calculated Atomic Weight |
Atomic Symbol |
Atomic Number |
Atomic Weight |
Calculated Atomic Number |
Calculated Atomic Weight |
|
H |
1 |
1.00794 |
1.0000 |
1.0000 |
Rh |
45 |
102.90550 |
44.9180 |
103.3614 |
|
He |
2 |
4.002602 |
2.0047 |
4.0070 |
Pd |
46 |
106.421 |
46.0430 |
109.2902 |
|
Li |
3 |
6.941 |
3.2187 |
6.9375 |
Ag |
47 |
107.8682 |
47.1680 |
109.2902 |
|
Be |
4 |
9.012183 |
4.2187 |
9.0000 |
Cd |
48 |
112.411 |
48.0820 |
112.4398 |
|
B |
5 |
10.811 |
5.0937 |
10.8047 |
In |
49 |
114.818 |
49.4180 |
115.2189 |
|
C |
6 |
12.0107 |
5.6875 |
12.0156 |
Sn |
50 |
118.710 |
50.1641 |
118.6591 |
|
N |
7 |
14.0067 |
7.0156 |
14.7754 |
Sb |
51 |
121.760 |
50.8437 |
121.8841 |
|
O |
8 |
15.9994 |
7.6250 |
15.9844 |
Te |
52 |
127.603 |
52.4141 |
126.0700 |
|
F |
9 |
18.9984032 |
9.0625 |
18.9766 |
I |
53 |
126.90447 |
52.6953 |
126.8111 |
|
Ne |
10 |
20.1797 |
9.6406 |
20.1895 |
Xe |
54 |
131.293 |
54.3828 |
131.2577 |
|
Na |
11 |
22.9897693 |
11.0195 |
23.0352 |
Cs |
55 |
132.905452 |
55.0937 |
133.1504 |
|
Mg |
12 |
24.3050 |
11.6562 |
24.3406 |
Ba |
56 |
137.327 |
56.4375 |
136.9203 |
|
Al |
13 |
26.9815386 |
13.0195 |
27.2727 |
La |
57 |
138.90547 |
57.0937 |
138.7816 |
|
Si |
14 |
28.0855 |
14.4141 |
28.1023 |
Ce |
58 |
140.116 |
57.5937 |
140.1895 |
|
P |
15 |
30.973762 |
15.0195 |
31.5102 |
Pr |
59 |
140.90765 |
59.0937 |
144.4129 |
|
S |
16 |
32.065 |
16.2891 |
32.0750 |
Nd |
60 |
144.242 |
60.0937 |
144.4129 |
|
Cl |
17 |
35.453 |
17.0195 |
35.7477 |
Pm |
61 |
145 |
61.3437 |
145.1168 |
|
Ar |
18 |
39.948 |
18.4766 |
38.8285 |
Sm |
62 |
150.362 |
62.2187 |
150.3961 |
|
K |
19 |
39.0983 |
19.0352 |
39.0898 |
Eu |
63 |
151.964 |
63.0937 |
155.6754 |
|
Ca |
20 |
40.078 |
19.9844 |
40.0855 |
Gd |
64 |
157.253 |
63.6875 |
157.3336 |
|
Sc |
21 |
44.955912 |
21.3203 |
44.9884 |
Tb |
65 |
158.92535 |
64.7187 |
158.8430 |
|
Ti |
22 |
47.867 |
22.4453 |
47.8928 |
Dy |
66 |
162.500 |
65.5937 |
162.7145 |
|
V |
23 |
50.9415 |
23.4297 |
50.4341 |
Ho |
67 |
164.93032 |
67.0937 |
166.9379 |
|
Cr |
24 |
51.9961 |
24.0625 |
52.0550 |
Er |
68 |
167.259 |
68.2187 |
167.2898 |
|
Mn |
25 |
54.938045 |
25.1875 |
54.9594 |
Tm |
69 |
168.93421 |
68.8437 |
169.0496 |
|
Fe |
26 |
55.845 |
25.5391 |
55.8798 |
Yb |
70 |
173.054 |
70.2187 |
172.9211 |
|
Co |
27 |
58.933195 |
26.7344 |
58.9639 |
Lu |
71 |
174.9668 |
70.9375 |
174.9313 |
|
Ni |
28 |
58.6934 |
28.0352 |
62.3248 |
Hf |
72 |
178.492 |
72.1875 |
178.4508 |
|
Cu |
29 |
63.546 |
29.0547 |
63.5038 |
Ta |
73 |
180.94788 |
72.5937 |
181.0160 |
|
Zn |
30 |
65.382 |
30.0742 |
65.4108 |
W |
74 |
183.841 |
74.0937 |
183.8316 |
|
Ga |
31 |
69.723 |
30.8828 |
69.6756 |
Re |
75 |
186.207 |
74.9375 |
186.1938 |
|
Ge |
32 |
72.641 |
32.0430 |
72.6717 |
Os |
76 |
190.233 |
76.3750 |
190.2141 |
|
As |
33 |
74.92160 |
32.9219 |
74.9380 |
Ir |
77 |
192.217 |
76.5937 |
192.2785 |
|
Se |
34 |
78.963 |
34.4687 |
78.9278 |
Pt |
78 |
195.084 |
78.0937 |
195.0941 |
|
Br |
35 |
79.904 |
34.8555 |
79.9326 |
Au |
79 |
196.966569 |
79.0937 |
200.7254 |
|
Kr |
36 |
83.798 |
36.3672 |
83.8344 |
Hg |
80 |
200.592 |
80.0937 |
200.7254 |
|
Rb |
37 |
85.4678 |
37.0430 |
85.5752 |
Tl |
81 |
204.3833 |
80.8750 |
204.2922 |
|
Sr |
38 |
87.621 |
37.7891 |
87.5331 |
Pb |
82 |
207.210 |
82.3750 |
207.1078 |
|
Y |
39 |
88.90585 |
38.8711 |
88.9101 |
Bi |
83 |
208.98040 |
83.0000 |
210.0000 |
|
Zr |
40 |
91.224 |
40.4180 |
91.5039 |
Po |
84 |
209 |
84.0937 |
211.9879 |
|
Nb |
41 |
92.90638 |
40.9805 |
92.9861 |
At |
85 |
210 |
85.0937 |
211.9879 |
|
Mo |
42 |
95.962 |
41.5430 |
97.4327 |
Rn |
86 |
222 |
86.4375 |
221.3891 |
|
Tc |
43 |
98 |
42.8516 |
97.9084 |
Fr |
87 |
223 |
87.0508 |
223.1328 |
|
Ru |
44 |
101.072 |
43.5312 |
101.1334 |
Ra |
88 |
226 |
88.2266 |
226.0156 |
|
Atomic Symbol |
Atomic Number |
Atomic Weight |
Calculated Atomic Number |
Calculated Atomic Weight |
Atomic Symbol |
Atomic Number |
Atomic Weight |
Calculated Atomic Number |
Calculated Atomic Weight |
|
Ac |
89 |
227 |
89.1719 |
226.9688 |
Rf |
104 |
267 |
104.0391 |
267.0859 |
|
Th |
90 |
232.03806 |
90.4961 |
231.5547 |
Db |
105 |
268 |
105.3906 |
268.0156 |
|
Pa |
91 |
231.03588 |
91.4102 |
231.0391 |
Sg |
106 |
271 |
106.0625 |
270.9883 |
|
U |
92 |
238.02891 |
92.4687 |
236.4375 |
Bh |
107 |
272 |
107.4375 |
271.9844 |
|
Np |
93 |
237 |
92.7266 |
237.0156 |
Hs |
108 |
270 |
108.4688 |
268.8789 |
|
Pu |
94 |
244 |
94.4336 |
241.1797 |
Mt |
109 |
276 |
109.1094 |
276.0313 |
|
Am |
95 |
243 |
95.2070 |
243.0703 |
Ds |
110 |
281 |
110.4922 |
279.5313 |
|
Cm |
96 |
247 |
96.4844 |
246.2188 |
Rg |
111 |
280 |
111.0391 |
280.5859 |
|
Bk |
97 |
247 |
96.8047 |
246.9844 |
Cn |
112 |
285 |
112.4688 |
283.3750 |
|
Cf |
98 |
251 |
98.4414 |
250.9766 |
Nh |
113 |
284 |
112.7891 |
283.9609 |
|
Es |
99 |
252 |
98.8633 |
252.0078 |
Fl |
114 |
289 |
114.4688 |
287.2109 |
|
Fm |
100 |
257 |
100.4609 |
255.9219 |
Mc |
115 |
288 |
114.8750 |
288.0156 |
|
Md |
101 |
258 |
101.3047 |
257.9844 |
Lv |
116 |
293 |
116.0000 |
291.5000 |
|
No |
102 |
259 |
101.7266 |
259.0156 |
Ts |
117 |
294 |
117.0000 |
292.8000 |
|
Lr |
103 |
262 |
102.5000 |
262.0000 |
Og |
118 |
294 |
118.0000 |
293.9000 |
Comparing the two equations shows there are slight difference between them . Also, the R- squared value for equations 1 and 2 are 0.996 and 0.997 which means, there is almost perfect correllation between the atomic numbers and the atomic weights in the two equations.
Unfortunately, Hydrogen dose not answer right in these two equations, we can consider that it is because Hydrogen dose not have neutron but other elements have. So, we cosider Hydrogen out of any equation, as it is always considered seperate of any group in the periodic table of elements. As for elements with atomic number 117 and 118 , a slight change in the slop of curve can be seen in figure 5a and 5b. If we consider equation 1 and place atomic numbers 117
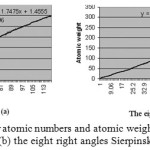 |
Figure 5: plot and equation for atomic numbers and atomic weights for (a) the periodic table of elements (b) the eight right angles Sierpinski triangles Click here to View figure |
Table 5: %Error in calculated Atomic Number and calculated Atomic Weight by seven period Sierpinski right angled triangles algorithm
|
Atomic Symbol |
% Error in Atomic Number |
%Error in Atomic Weight |
AtomicSymbol |
% Error in Atomic Number |
% Error in Atomic Weight |
Atomic Symbol |
% Error in Atomic Number |
% Error in Atomic Weight |
|
H |
0.0000 |
0.7877 |
Nb |
0.0476 |
0.0858 |
Tl |
0.1543 |
0.0446 |
|
He |
0.2350 |
0.1099 |
Mo |
1.0881 |
1.5326 |
Pb |
0.4573 |
0.0493 |
|
Li |
7.2900 |
0.0504 |
Tc |
0.3451 |
0.0935 |
Bi |
0.0000 |
0.4879 |
|
Be |
5.4675 |
0.1352 |
Ru |
1.0654 |
0.0607 |
Po |
0.1115 |
1.4296 |
|
B |
1.8740 |
0.0583 |
Rh |
0.1822 |
0.4430 |
At |
0.1102 |
0.9466 |
|
C |
5.2083 |
0.0408 |
Pd |
0.0935 |
2.6961 |
Rn |
0.5087 |
0.2752 |
|
N |
0.2257 |
5.4881 |
Ag |
0.3574 |
1.3183 |
Fr |
0.0584 |
0.0595 |
|
O |
4.6875 |
0.0937 |
Cd |
0.1708 |
0.0256 |
Ra |
0.2575 |
0.0069 |
|
F |
0.6944 |
0.1148 |
In |
0.8531 |
0.3492 |
Ac |
0.1932 |
0.0137 |
|
Ne |
3.5940 |
0.0486 |
Sn |
0.3282 |
0.0429 |
Th |
0.5512 |
0.2083 |
|
Na |
0.1773 |
0.1976 |
Sb |
0.3065 |
0.1019 |
Pa |
0.4508 |
0.0014 |
|
Mg |
2.8650 |
0.1465 |
Te |
0.7963 |
1.2014 |
U |
0.5094 |
0.6686 |
|
Al |
0.1500 |
1.0791 |
I |
0.5749 |
0.0736 |
Np |
0.2940 |
0.0066 |
|
Si |
2.9578 |
0.0598 |
Xe |
0.7089 |
0.0269 |
Pu |
0.4613 |
1.1559 |
|
P |
0.1300 |
1.7319 |
Cs |
0.1704 |
0.1843 |
Am |
0.2179 |
0.0289 |
|
S |
1.8069 |
0.0312 |
Ba |
0.7812 |
0.2961 |
Cm |
0.5046 |
0.3163 |
|
Cl |
0.1147 |
0.8312 |
La |
0.1644 |
0.0892 |
Bk |
0.2013 |
0.0063 |
|
Ar |
2.6478 |
2.8024 |
Ce |
0.7005 |
0.0524 |
Cf |
0.4504 |
0.0093 |
|
K |
0.1853 |
0.0217 |
Pr |
0.1589 |
2.4876 |
Es |
0.1381 |
0.0031 |
|
Ca |
0.0780 |
0.0187 |
Nd |
0.1562 |
0.1185 |
Fm |
0.4609 |
0.4195 |
|
Sc |
1.5252 |
0.0723 |
Pm |
0.5634 |
0.0805 |
Md |
0.3017 |
0.0061 |
|
Ti |
2.0241 |
0.0539 |
Sm |
0.3527 |
0.0227 |
No |
0.2680 |
0.0060 |
|
V |
1.8682 |
0.9960 |
Eu |
0.1487 |
2.4423 |
Lr |
0.4854 |
0.0000 |
|
Cr |
0.2604 |
0.1133 |
Gd |
0.4883 |
0.0512 |
Rf |
0.0376 |
0.0322 |
|
Mn |
0.7500 |
0.0389 |
Tb |
0.4328 |
0.0518 |
Db |
0.3720 |
0.0058 |
|
Fe |
1.7727 |
0.0623 |
Dy |
0.6156 |
0.3120 |
Sg |
0.0590 |
0.0043 |
|
Co |
0.9837 |
0.0521 |
Ho |
0.1398 |
1.2172 |
Bh |
0.4089 |
0.0057 |
|
Ni |
0.1257 |
6.1871 |
Er |
0.3216 |
0.0184 |
Hs |
0.4341 |
0.4152 |
|
Cu |
0.1886 |
0.6641 |
Tm |
0.2265 |
0.0683 |
Mt |
0.1004 |
0.0113 |
|
Zn |
0.2473 |
0.0440 |
Yb |
0.3124 |
0.0768 |
Ds |
0.4474 |
0.5227 |
|
Ga |
0.3781 |
0.0680 |
Lu |
0.0880 |
0.0203 |
Rg |
0.0352 |
0.2092 |
|
Ge |
0.1344 |
0.0423 |
Hf |
0.2604 |
0.0231 |
Cn |
0.4186 |
0.5702 |
|
As |
0.2367 |
0.0219 |
Ta |
0.5566 |
0.0371 |
Nh |
0.1866 |
0.0138 |
|
Se |
1.3785 |
0.0446 |
W |
0.1266 |
0.0051 |
Fl |
0.4112 |
0.6191 |
|
Br |
0.4128 |
0.0358 |
Re |
0.0833 |
0.0071 |
Mc |
0.1087 |
0.0054 |
|
Kr |
1.0200 |
0.0434 |
Os |
0.4934 |
0.0099 |
Lv |
0.0000 |
0.5119 |
|
Rb |
0.1162 |
0.1257 |
Ir |
0.5277 |
0.0320 |
Ts |
0.0000 |
0.4082 |
|
Sr |
0.5550 |
0.1003 |
Pt |
0.1201 |
0.0052 |
Og |
0.0000 |
0.0340 |
|
Y |
0.3305 |
0.0048 |
Au |
0.1186 |
1.9084 |
|||
|
Zr |
1.0450 |
0.3068 |
Hg |
0.1171 |
0.0665 |
And 188, the calculated atomic weights are, respectively , 296.0662 and 298.2122. The interesting point is these numbers are resulted by the eight right angled Sierpinski triangles method. We can assume that these two elements should have such weights but for they are the heaviest and also radioactive elements, some of their masses reduced and transformed to energy. To guess the atomic weights of eighth period, with considering the calculated weights of the elements 117 and 118 by the equation 2, we decided to make slightly change on one coefficient on the equation2. This change may be indicated as reduced mass released as radioactive energy. The resulted equation is
*y =-8 10-5×3 + 0.015×2 +1.7531x +1.4274 (Eq.3)
The atomic numbers of eighth period and their atomic weights which are calculated by the equation 3 (Eq.3) are listed in table 6. However the elements of the eighth period of the periodic table have not yet discovered, so we can not determine their errors, but we can assumed their atomic weights and by this resulted equation and hope that their correlation with their atomic weight will be a kind of Sierpinski triangle fractals . The R- squared value for the numbers in table 6 is 1 which shows a complete correlation between the atomic numbers and their calculated atomic weights. If a discovered element shows a weight more or less than what is calculated in the table 6, we may relate it to the amount of masses which are transformed to energy.
Table 6: The atomic numbers of eight period elements and their calculated atomic weights with equation 3
|
Atomic |
Atomic |
Atomic |
Atomic |
Atomic |
Atomic |
Atomic |
Atomic |
|
Number |
Weight |
Number |
Weight |
Number |
Weight |
Number |
Weight |
|
117 |
283.746 |
126 |
300.428 |
135 |
314.641 |
144 |
326.035 |
|
118 |
285.711 |
127 |
302.136 |
136 |
316.053 |
145 |
327.112 |
|
119 |
287.649 |
128 |
303.812 |
137 |
317.429 |
146 |
328.149 |
|
120 |
289.559 |
129 |
305.457 |
138 |
318.769 |
147 |
329.146 |
|
121 |
291.443 |
130 |
307.07 |
139 |
320.074 |
148 |
330.103 |
|
122 |
293.298 |
131 |
308.651 |
140 |
321.341 |
149 |
331.018 |
|
123 |
295.124 |
132 |
310.199 |
141 |
322.572 |
150 |
331.892 |
|
124 |
296.922 |
133 |
311.714 |
142 |
323.765 |
||
|
125 |
298.69 |
134 |
313.195 |
143 |
324.919 |
Conclusion
Fractal geometries are found in nature and the whole world around us . One of this fractals is Sierpinski triangle. In this paper, with help of softwares such as MATLAB and Ecxel , we show that there is a correlation between the atomic numbers and atomic weights of the periodic table of elements and it is as right angle Sierpinski triagle fractals type.With making more triangle on the hypotenuse of the initial Sierpinski triangle, %errors will be reduced and calculated numbers will be closer to real ones. With the equations obtained with Sierpinski triangle algorithm we may guess the atomic weights of future discovered elements.
References
- Layek, G.C. An introduction to dynamical systems and chaos, Chapter 13; Fractals, Springer India,. 2015.
- Lutz, Jack H.; Shutters, Brad. Approximate self-assembly of the Sierpinski triangle. Springer. 2011.
- Majewski, Mirek. A tutorial on the realistic visualization of 3D Sierpinski fractals .Comput.& Geaphics, 1998 , 22, .1,129-142.
- Sarkar, Rajarshi; Guo, Kai; Moorefield, Charles N.; Saunders, Mary Jane; Wesdemiotis, Chrys ; Newkome, George R.. One-Step Multicomponent Self-Assembly of a First-Generation Sierpinski Triangle: From Fractal Design to Chemical Reality. Angew. Chem. Int.Ed. 2014.53 , 1 –5.
- Frame, Michael ; Martino, William. Fractal and multifractal geometry: Scaling symmetry and statistics. Advanced review. 2012. 4. Wiley Periodicals, Inc.
- Lathrop, James I.; Lutz, Jack H.; Summers, Scott M.. Strict Self-assembly of Discrete Sierpinski Triangles. Springer, Berlin, B . 2007. LNCS 4497. 455–464,.
CrossRef - Kautz, S.M.; Lathrop, J.I.: Self-assembly of the Sierpinski carpet and related fractals. The Fifteenth International Meeting on DNA Computing and Molecular Programming. Lecture Notes in Computer Science, 2009. 5877. 78–87. Springer, Berlin
- Lathrop, J.I.; Lutz, J.H.; Summers, S.M.: Strict self-assembly of discrete Sierpinski triangles. Theor .Comput. Sci. 2009. 410, 384–405.
CrossRef - Olsen, L. Distribution of digits in integers: fractal dimension and zeta functions. Acta Arith. 2002.105(3), 253–277 .
- Singh, Amandeep; Singh, Surinder. A modified coaxial probe-fed Sierpinski fractal wideband and highgain antenna. Int. J. Electron. Commun. (AEÜ). 2015. 69. 6.884-889.
- Singh, Amandeep; Singh, Surinder. Design and optimization of a modified Sierpinski fractal antenna for broadband applications. Applied Soft Computing, 2016. 38 , 843-850.
CrossRef

This work is licensed under a Creative Commons Attribution 4.0 International License.









