Physical Chemistry Properties of Fe3O4 @ Cyclodextrin@ (12, 12) Swcnts as a Catalyst

Introduction

The great temperature shifts catalyst (HTS) of iron oxide^1-3 stabilized by chromium oxide^1-5. This chrome-iron alloys as a catalyst is diminished at chemical-reactor-start up for generating Fe₃O₄ from α-Fe₂O₃⁴ and Cr₂O₃⁵. Fe₃O₄ is one of the most important electrical conductors within conductivities considerably higher comparison to Fe₂O₃^3,4  and this is imputed for exchange electron between two parts of the Fe^(II) and Fe^(III) centers^1-3.

Fe₃O₄ family are ferromagnetic with remarkable curie temperature (858 K) and this ferromagnetism properties of Fe₃O₄ appears because the spin electron of the Fe^(II)  and Fe^(III)  ions are coupled together in the octahedral structures and the spin of the Fe^(III) ion are coupled (anti-parallel to the former^1-4) in a tetrahedral structure. Fe₃O₄ is used in the water gas shift reaction as a catalyst in the “Haber process”

Magnetite (Fe3O4) is structured in the inverse-cubic-spinel-crystal⁴. Each of cubic-spinel-cell contains “8” inter-penetrating oxygens within the tetrahedral sites^4,5 and has been occupied through “1/3” of the Fe atoms, such as diamond structures. The other iron atoms are placed at the octahedral situations with closest atoms arranged as string in six various directions^5-7 .

Fe₃O₄ structures consist of the cubic-close-packed arrays of oxides which all of the Fe⁽²⁺⁾ ions occupies “1/2” of the octahedral locations and the Fe⁽³⁺⁾ splits equally along the other octahedral and tetrahedral locations^1-7.

Cyclo-dextrin is extracted from the degradation⁵ of starch by Bacillusmacerans^5,6, which for the first one has been isolated in the late 9^th century^5-8. Its abilities for forming complexes with various organic molecules were discovered immediately there after^6-9. By developing the fields of Chemistry’s Supramolecular⁸, its complexation properties have been tightly studied^7-10 .Usage of cyclo-dextrin and its derivatives are desirable in various areas of chemistry^7-10, including the influencing of the organic molecules^8-14. By this study the catalysis’s properties of Fe3O4 nanoparticles @ Cyclodextrins @ (12, 12) SWCNTs for comparing in the area of chemical synthesizes^15-20 have been investigated.

CNT or carbon nanotubes are representatives of Nano materials. CNT is a cylindrically²¹ shaped- carbon-material²² with the Nano metric diameter^21-30. Their shapes which are in the structure of hexagonal-mesh^23-28,look like a graphite^26-30 and these sheets have wrapped and their two edges have attached together seamlessly^31-35.

Although it is a common-place material using in pencil-leads^31-33, their unique structures causes them for presenting a characteristic which had not observed with any other materials^30-35. SWCNTs is classified³³ into (1): single-walled of carbon-Nano- tubes (CNTs) , (2): double-walled carbon-Nano- tubes (CNTs), (3): multi walled carbon-Nano- tubes (CNTs)  according to the number³⁷ of the layers in a rolled-graphite^36-39.

The important attentions in this area are about the SWCNTs diameters, which are varying among (0.4 – 2) nanometer^35-40 while the lengths are in the order of microns(10^-6m)^32-40, but SWCNTs with the lengths in the order of centimeters have also been observed recently^41-44.

The extremities of the SWCNTs have been nearest with the lids⁴⁶ of the graphite sheets^45-50.

Computational Details

A section of our system for Fe3O4@Cyclodextrins nanoparticles and Fe3O4@ (12, 12) CNTs have been simulated with QM/MM methods and the optimization were carried out^51-55 via the Monte Carlo approaches. These investigations with differences in the force fields are illustrated through comparing^52-56 the energies by the force fields of AMBER⁵⁷ and OPLS⁵⁸. In addition, the software of Hyper-Chem professional version of 7.01 is used for further calculation.

In the noncovalent interaction of two parts of Fe3O4 and Cyclo-dextrin, the density functional methods such as B3LYP are not suitable for describing the van-der-Waals forces in medium⁵⁵ ranges interaction. So, the QM/MM such as ONIOM method with three classes of (1): high, (2): medium, and (3): low calculations, has been used in this studies between two parts of Fe3O4 and Cyclo-dextrin.

The ab-initio of DFT methods are used for the model of systems through definition of  ONIOM^53-56 layers and the various semi-empirical⁵⁵ methods such as pm6 within pseudo=lanl2⁵⁷ order and the Pm3MM⁵⁸ for the second and third  layers, respectively⁵⁹.

The most general of density-functional-theory are inexpressive to exhibit the correlation⁵⁶ and exchange⁵⁷ energies for medium-range of non-bonded systems correctly. In addition, some of the recent works have exhibited the inexactitude of the medium-ranges exchange energies lead to the large principled error in prognostication of the molecular properties^51-53.

Electronic structure calculations and geometry optimization have been performed using the m06-DFT. This Functional theories are based on an repetition solution of the Kohn&Sham equation^53,54 of DFT theory in the plane-wave sets including a projector-augmented-wave-pseudo potential^50-54. The PBE⁵⁵ (Burke, Ernzerh &Perdew), XC (exchange/correlation) of the GGA (generalized-gradient-approximation) are also has applied. The calculation of the lattice- constant⁵⁷ and the atomic coordinate is made by the minimized the systems for the total energies.

The charges transfer⁵⁶ of electrostatics potentials derived⁵⁷ charges were also estimated using MKS(Merz-Kollman-Singh) and Chelp or chelpG^56,57 . The charges calculation method based on electrostatic-potentials fitting or MESP are not well befit for remedy of the bigger system.

By these conditions, changes of the inner-most atomic-charge would not topped toward a remarkable changes of the MESP^50-56 for  the molecules, which means that the precise value for the inner-most atomic-charge is not well specified out-side molecules . The agent atomic charge for a molecule might be calculated as the intermediate value over a few molecular conformations^50-54.

In an overview of the effect of the basis sets and the “Hamiltonian” on the charges distributions would be found in the references^56-58 .The charges densities profile in this kind studies have been extracted from the first principle calculations via an intermediate processing as explained in the references^53,54. The interaction energies of these non-bonded interactions were calculated according to the equation as follows for all items:

Where the “ΔE_s ” are the stability energies.

Both electron densities of Laplacian and gradient, values of orbital-wave-functions, spin-electron densities, total potential of electrostatics (ESP), electrostatic potential from atomic charges of nucleus, ELF(localization-function for electron ), LOL (locator&orbital-localized), detailed by correlation hole, as well as the correlation &exchange densities, Becke & Tsirelson, correlation-  factor, and the expectation of ionization energies (local) using the Multifunctional^55-57 have also been applied in these kind  studies. The contour lines maps were also drawn using the Multi-wfn software^55-57. The contour lines corresponding to the VdW surfaces including of electron densities are defined by Bader and has been drawn in this study^55-57. That is clearly useful for analyzing of distributions for the electrostatics potentials on VdW surfaces. Those contour⁵⁵ lines have also been drawn in the gradient-lines⁵⁵ and vector-fields-maps⁵⁶ by the equal option^55-57. The relief⁶² maps were applied for presenting the height values at the points. Shaded-surface⁶¹ maps with and without a projection⁵⁶ is used in our representation⁵⁶ of height values at various situation^60-62.

Result and Discussion

Monte-Carlo Approaches

The section of ab-initio methods are given by computation that is yielded from principals of theory phenomenon, without inclusion of the experiment information^63,64. The important usual types of ab-initio optimization are called HF, while the primary approximations are called: central-field or CFA. An important method that eschews making the HF problems is popular as the name Quantum-Monte-Carlo^*. Also in contrast to the molecular dynamics methods which are totally definitive, the Monte Carlo simulation methods are based on using of stochastic significances. On those methods, the systems are included of M atoms which are given in a group of primary orients and interact together. Estimations of those primary configurations are then produced by this consecutive random displacement which works through variation of QMC^*, Green’s functions and diffusion approaches. Those methods work via wave-functions and have evaluated the numerical integrals. Although those optimization might be much more time consuming, these are seems the most precise and suitable ways which are known up to now. An ab-initio calculation gives high quality results and then might yields increasingly high quanty results.

There are 3 levels for accomplishing of any QM/MM optimization in the “Hyper-Chem version 8.0” packages. Firstly sets up the structures of the molecules with an appropriate starting geometry or coordinates. For the second step it should be chosen suitable optimization including its associated-choices^*. For the 3^rd step it should be selected a kind of optimization with the related options. The MC simulation detects a so-called important phase-space^* region that is of the lowest energies. Because of fault of the force fields, these lower energies basin usually (in most cases) does not equal to the normal states, so the rank of native structures produced by the force fields themselves is low-order.

By this work, differences in the force-fields are investigated with comparison the energies optimization using force fields among the Amber, MM+, and OPLS of charmm. In addition, we investigated the polar solvents and the temperature effect (from 260K to 400K) for the stability of single wall of CNTs bonded to CGA or CFA by the various solvent. The QM or quantum mechanics calculation was carried out with the “Hyper-Chem 8.0” program.

This work basically accomplished on the magnetic properties of Fe₃O₄ in the non-bonding systems of Cyclo-dextrin (and Fe3O4. The non-bonding interactions are exhibited in figs 1- 3. As it is cleared in tables 1-10, the electrical⁵⁵ property can be yielded from changing in a non-bonding interaction. Potential energy, electron density, ELF, energy density⁵⁵, Ellipticity, LOL, eta indexes and ECP of Fe3O4@Cyclodextrin (@ (12, 12) SWCNTs were calculated of each simulations (Table 1-10)^55-59.

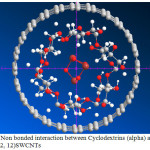Figure 1: Non bonded interaction between Cyclodextrins (alpha) and Fe3O4 Inside (12, 12)SWCNTs Click here to View Figure

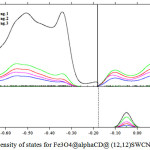Figure 2: Density of states for Fe3O4@alphaCD@ (12,12)SWCNNTS  Click here to View Figure

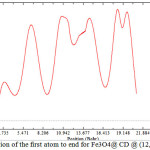Figure 3: position of the first atom to end for Fe3O4@ CD @ (12,12)SWCNNTs Click here to View Figure

 

Table 1: All Electron Densities of non-bonded interactions for Fe3O4- Cyclodextrin (α)@(12,12)SWCNTs

Atom(number)	Density of all electron (10-3)	Density of alpha (10-3)	Density of Beta (10-3)	Spin Density
Fe(1)	0.10	0.05	0.05	0.0
Fe(2)	0.20	0.10	0.10	0.0
Fe(3)	0.34	0.17	0.17	0.0
O(4)	0.30	0.15	0.15	0.0
O(5)	0.13	0.65	0.65	0.0
O(6)	0.36	0.18	0.18	0.0
O(7)	0.24	0.12	0.12	0.0

 

Table 2: All Electron Energies of non-bonded interactions for Fe3O4- Cyclodextrin (α)@(12,12)SWCNTs

Atom(number)	Lagrangian kinetic [G(r)] energy (10-3)	Hamiltonian kinetic [K(r)] energy (10-3)	Potential energy Density [U(r)] (10-3)
Fe(1)	0.24	0.45	-0.32
Fe(2)	0.28	0.6	-0.42
Fe(3)	0.12	0.26	-0.60
O(4)	0.26	-0.14	-0.32
O(5)	0.32	-0.20	-0.56
O(6)	0.28	-0.10	-0.22
O(7)	0.10	-0.20	-0.80

 

Table 3: Laplacian, ELF, LOL and Local information entropy of non-bonded interactions for Fe3O4- Cyclodextrin (α)@(12,12)SWCNTs

Atom (number)	Laplacian of electron density (10-1)	Electron localization function (ELF) (10-3)	Localized orbital locator (LOL) (10-1)	Local information entropy (10-4)
Fe(1)	-0.12	0.62	0.25	0.12
Fe(2)	-0.16	0.42	0.36	0.14
Fe(3)	-0.28	0.38	0.16	0.46
O(4)	0.42	0.26	0.24	0.26
O(5)	0.32	0.16	0.12	0.26
O(6)	0.56	0.18	0.22	0.34
O(7)	0.26	0.22	0.10	0.10

 

Table 4: Average local ionization energy, RDG and ESP of non-bonded interactions for Fe3O4- Cyclodextrin (α) @(12,12)SWCNTs

Atom (number)	Reduced density gradient (RDG) (10+1)	Average local ionization energy	ESP from nuclear charge (104)	ESP from electron charge (102)
Fe(1)	0.40	0.46	0.10	-0.42
Fe(2)	0.40	0.46	0.14	-0.48
Fe(3)	0.52	0.56	0.14	-0.42
O(4)	0.62	0.72	0.16	-0.42
O(5)	0.16	0.16	0.14	-0.42
O(6)	0.62	0.80	0.16	-0.42
O(7)	0.16	0.20	0.18	-0.64

 

Table 5: Lambada2, Wave function value, Ellipticity of electron density and Eta index of non-bonded interactions for Fe3O4- Cyclodextrin (α) @(12,12)SWCNTs

Atom(number)	Lambada2(10-3)	Wave function value (10-4)	Ellipticity of electron density	Eta index
Fe(1)	-0.16	0.42	0.48	-3.41
Fe(2)	-0.13	0.88	0.44	-2.54
Fe(3)	-0.15	0.67	0.23	0.53
O(4)	0.36	0.29	-0.46	1.41
O(5)	0.11	-0.43	-0.17	0.93
O(6)	0.34	0.33	-0.42	0.38
O(7)	0.23	-0.28	-0.17	0.76

 

Conclusion

Fe₃O₄ is Ferro-magnetic including a curie^* temperature of the 858+0.5 K and these Ferro-magnetism arises for “Fe3O4” because the spin of electrons for the Fe^III and Fe^II in the octahedral location are in a coupled situations together and those spins of the Fe^(III) ions in the tetrahedral locations are also coupled together but are in anti-parallel^* situations to the previous one. Fe₃O₄ is used in the water gas shift reaction as a catalyst in the “Haber process”. It has been emphasized this study have great potentials for developing the novel multi-functional catalysts with high selectivity and reactivity. The other amazing developments are using the (12,12) single wall Nano tube carbon over the magnetic nano-particles that causes useful removal of transition metals based catalyst in drug chemistry. These approaches should find relevant industrials applications in food additive, biopharmaceutical, fragrance and others.

References

1. Greenwood, Norman N.; Earnshaw, Alan, Chemistry of the Elements, 1997 (2nd ed.), Butterworth-Heinemann .
2. Ma, Ming; Zhang, Yu; Guo, Zhir4.ui; GU, Ning, Nanoscale Research Letters, 2013, 8 (1), 16.
   CrossRef
3. Massart, R.; IEEE transactions on magnetics, 17, 2, 1981, 1247–1248.
4. Schardinger, F.; Zentralbl. Bakteriol. Abt. II 1911, 29, 188-197; (b) Freudenberg, K.; Schaaf, E. Dumpert, G.; Ploetz, T. Naturwissenschaften, 1937, 27, 850-853.
5. Wenz, G. Angew. Chem. Int. Ed. Engl. 1994, 33, 803-822
   CrossRef
6.  Ueno, A. Supramol. Sci. 1996, 3, 31-36
   CrossRef
7. Monajjemi, M.  Biophysical Chemistry. 2015 207,114 –127
   CrossRef
8.  Bagheri,S.; Moosavi,M.S.; Moradiyeh,N.; Zakeri,M.; Attarikhasraghi,N.; Saghayimarouf,N.; Niyatzadeh,G.; Shekarkhand,M.; Mohammad S. Khalilimofrad, Ahmadin,H.; Ahadi,M.; Molecules 2015, 20, 21636–21657.
9. Monajjemi, M.  Theor Chem Acc, 2015, 134:77
   CrossRef
10.  Monajjemi, M.  Journal of Molecular Modeling , 2014, 20, 2507
    CrossRef
11. Lee, V.S.; Khaleghian, M.; B. Honarparvar, B.; F. Mollaamin, F. J. Phys.Chem C. 2010, 114, 15315
12. Whittembury G. J Gen Physiol.1960, 43, 43-56
    CrossRef
13. Valter, Ström; Richard T.; Olsson, K. V. Rao. J. Mater. Chem, 2010, 20, 4168-4175
14. Mei Fang, Valter Ström, Richard T. Olsson, Lyubov Belova, K. V. Rao, Rapid mixing: Appl. Phys. Lett.2011, 99, 222501
    CrossRef
15.  Villiers, A. Compt. Rend. 1891, 112, 536-539.
16. Monajjemi, M. Struct Chem. 2012, 23,551–580
    CrossRef
17. Monajjemi, M.;  Boggs, J.E.  J. Phys. Chem. A, 2013, 117, 1670 −1684
    CrossRef
18.  Monajjemi, M.; Khaleghian, M, Journal of Cluster Science. 2011, 22 (4), 673-692 318
19. Monajjemi, M. Chemical Physics. 2013, 425, 29-45
    CrossRef
20. Monajjemi, M.; Wayne Jr, Robert. Boggs, J.E.  Chemical Physics. 2014, 433, 1-11
21. Mahdavian, L.;  Mollaamin, F.; Honarparvar,B.; Fullerenes, Nanotubes and Carbon Nanostructures,2010, 18 (1), 45-55, 2010
22. Farmer RE.; Macey RI. BiochiBiophys Acta, 1970, 196, 53-65.
    CrossRef
23. Sidel,VW. Solomon AK. J Gen Physiol .1957, 41, 243-257.
    CrossRef
24. Monajjemi, M. Falahati, M.; Mollaamin, F.; Ionics, 2013, 19, 155–164.
    CrossRef
25. Tahan, A.; Mollaamin, F.; Russian Journal of Physical Chemistry A, 2009, 83 (4), 587-597
26. Ketabi, S.; Amiri, A. Russian Journal of Physical Chemistry, 2006, 80 (1), S55-S62
27. Monajjemi, M.; Baheri, H.; Mollaamin, F.  Journal of Structural Chemistry.2011 52(1), 54-59
    CrossRef
28. X.  Blasé.; A.  Rubio.; S.G. Louie.; M.L.  Cohen.; Europhys. Lett, 1994.28, 335.
29. N.G. Chopra.; A. Zettl.; Solid State Commun 1998, 105, 297.
    CrossRef
30. Monajjemi, M.; Heshmat, M.; Haeri, HH, Biochemistry (Moscow), 2006, 71 (1), S113-S122
    CrossRef
31. Honarparvar, B.; Nasseri, S. M. .; Khaleghian M. Journal of Structural Chemistry. 2009, 50, 1, 67-77
    CrossRef
32.  Monajjemi, M.; Honarparvar, B. H. ; Haeri, H. ; Heshmat ,M.;  Russian Journal of  Physical Chemistry C. 2006, 80(1):S40-S44CrossRef
33. Mollaamin, F.; Gharibe, S.; Int. J. Phy. Sci, 2011, 6, 1496-1500
34. Mollaamin, F.; Najafpour, J.; Ghadami, S.; Ilkhani, A. R.; Akrami, M. S,. Journal of Computational and Theoretical Nanoscience. 2014, 11 (5), 1290-1298
    CrossRef
35.  Monajjemi, M.; Mollaamin, F. Journal of Cluster Science, 2012, 23(2), 259-272
    CrossRef
36.  Monajjemi, M.; Khaleghian, M.; Mollaamin, F.   Molecular Simulation. 2010, 36, 11,  865– 870.
    CrossRef
37.  Mahdavian, L.; Mangkorntong, N. Fullerenes, Nanotubes and Carbon Nanostructures, 2009, 17 (5), 484-495
    CrossRef
38. J. Cumings.; A. Zettl, Solid State Commun.2004, 129, 661
    CrossRef
39. R. Ma.; Y. Bando.;  H. Zhu.; T. Sato, C. Xu, D. Wu, J. Am.Chem. Soc.2002, 124, 7672,
    CrossRef
40. Afsharnezhad, S, Jaafari, M.R..; Mirdamadi, S..; Mollaamin, F..; Monajemi, H. Chemistry .2008, 17 (1), 55-69
41. Mollaamin, F.; Monajjemi, M. Physics and Chemistry of Liquids .2012, 50,  5,  2012, 596–604
42. Chahkandi B, Zare K, Amiri A. Biochemistry (Mosc). 2005 ,70(3):366-76.
    CrossRef
43. Lee, V.S.; Nimmanpipug, P.; Mollaamin, F.; Kungwan, N.; Thanasanvorakun, S.; Russian Journal of Physical Chemistry A, 2009, 83, 13, 2288–2296
44. Jalilian,H.; Monajjemi, M. Japanese Journal of Applied Physics. 2015, 54, 8, 08510
45. Naderi, F.; Mollaamin, F.; Khaleghian, M.  J. Mex. Chem. Soc. 2012, 56(2), 207-211
46. Grimme, S. Angew Chem Int Ed, 2006, (45), 4460–4464, DOI: 10.1002/anie.200600448.
    CrossRef
47. Schreiner, P.R.; Fokin, A. A.; Pascal, R. A Jr.; de Meijere, A. Org. Lett, 2006, (8): 3635–3638.
    CrossRef
48. Zhao, Y.; Truhlar, D.G. Org. Lett, 2006, (8):5753–5755.
    CrossRef
49. Kohn, W.; Sham, LJ. Phys. Rev, 1965, (140) A: 1133-1138.
50.  Perdew, J .P. Burke, K.; Phys. Rev. Lett.1996, (77): 3865-3868.
    CrossRef
51. Besler, B.H.; Merz, K.M.; Kollman, P.A. J. comp. Chem, 1990, (11): 431-439,
52. Chirlian, L.E.; Francl, M.M. J.comp.chem, 1987, (8): 894-905, DOI: 10.1002/jcc.540080616
    CrossRef
53. Brneman, G.M, Wiberg, K.B. J. Comp Chem, 1990, (11): 361
54. Balderchi, A.; Baroni, S.; Resta, R. Phys. Rev. Lett, 1998, (61): 173.
55. Lu, T.; Chen, F. Acta Chim. Sinica, 2011, 69, 2393-2406.
56. Lu, T.; Chen, F J. Mol. Graph. Model, 2012, (38): 314-323.
    CrossRef
57. Lu, T.; Chen F. J. Comp. Chem. 2012, (33) 580-592.
58. Naghsh,F, oriental journal of chemistry, 2015, 31(1).,465-478
59. Chitsazan, A, oriental journal of chemistry, 2015, 31(1)., 393-408

---

This work is licensed under a Creative Commons Attribution 4.0 International License.