Optimization Central Composite Design for The Simultaneous Determination of Cd(II) Ions in Fruit and Vegetable Samples by Adsorptive Stripping Voltammetry

Introduction

Cadmium is known to be a hazardous environmental pollutant with toxic effects. Adverse effects of cadmium are produced not only because of its high toxicity in humans and animals, even at trace concentrations, but also due to bioaccumulation processes in almost all organs. The main target organs affected by cadmium are lungs, kidney, bones and teeth.

The concentration of cadmium in various samples is low, so sensitive  and selective methods for determination of cadmium in environmental samples are  required. Sensitive methods for  the determination of  trace amounts  of metal ions  in  natural samples have received much attention and many techniques have been employed.

Analysis of heavy metals at trace levels in fruit and vegetable samples are very important in the field of environmental analysis due to their important roles in life. For that, atomic absorption techniques have been usually used. However, they offer  many difficulties due to insufficient detection limits and/or matrix interferences of real samples and a preconcentration step is often required^1-4.

The   use   of  electroanalytical techniques  is  another alternative  widely employed, specially the stripping voltammetry. These methods are  well-established for trace metal analysis and adsorp- tive processes (AdSV) can further lower detection limits of stripping voltammetry to  the picomolar concentration levels. In  addition, these techniques are inexpensive, simple, quick and very useful for saline matrices like  seawater and estuarine water samples and for speciation studies^1-6.

The previous study, to find optimization in the determination of trace metals Cd, Cu, Pb and Zn^1-3 and  trace metals Fe, Co, Ni and Cr⁴ in both individual and simultaneous  by adsorptive stripping volt  ammetry (AdSV), carried out by observing the effect of one variable is changed, while the other variables are kept at a constant level. This optimization technique is called optimization of one variable or a factor at the current time.The main drawback of the results of the optimization of the factors that such optimization does not take into account the effect of the interaction between the variables studied. Therefore, this technique does not describe the full effect on the response parameter⁷. Another disadvantage of optimization of these factors is the increase in the number of trials required to do research, which leads to increased time and increased consumption of reagents and materials. To overcome this problem, an optimization technique of analytical procedures is by using multivariate statistical techniques^7-9.

The most relevant multivariate techniques used in analytical optimization is the Response Surface Method (RSM) with a Central Composite Design (CCD). RSM is a collection of mathematical and statistical techniques, which are used for modeling and analysis of problems in a response that is influenced by several variables, whose purpose is to optimize the response or optimize these variables to achieve the best system performance^7-11. The RSM was done using   Minitab.

Adsorptive stripping voltammetry is a highly sensitive technique¹², the response obtained in the form of the peak current (Ip) is influenced by variables (parameters) the following, namely:  calcon concentration, pH , accumulation potential and accumulation time. Therefore it is very important to determine the optimization of these parameters, which will affect the measurement of the peak flow in order to improve the quality of analytical results^8-10. The research design used in this study, as a tool for optimization was  central composite design with 4 variables, 3 level/degree and 31 a combination of treatments. The first step of 2k factorial design optimization are: provide the code, where the value of the highest level (+1), the lowest level (-1) and code (0) as the center point. Programs for statistical data processing Minitab 16 using Response Surface Methodology.

The purpose of this study was to obtain the optimum condition of cadmium, so it can be applied to the analysis of cadmium in fruit and vegetable samples.  To  achieve  these  objectives,  required  an  optimization technique  using  analytical  procedures  that RSM with a CCD^7-14. Some parameters were studied : variations of calcon concentration, pH, accumulation potential and   accumulation time.

Experimental  Section

Materials

Reagents were used in this study is a pure reagent, because stripping voltammetry is an ultra-sensitive method of analysis. The most important principle to remember is that an ultra-sensitive method of analysis, all chemicals must be pure (pa) and the equipment to be very clean and should be careful in its use. It aims to avoid or protect from contamination. Voltammetric measurements were carried out using a Metrohm 797 VA. Electrode stand with a multimode  electrode (MME)  operating in the HMDE mode. An  Ag/AgCl/KCl reference electrode and a platinum wire auxilary electrode were used. pH meter 80 models Griffin, Griffin & George Loughborough, England; and analytical balance Mettler AE 200, Toledo OH-USA; and glassware used in the laboratory

Work Procedure

To the vessel volammetry, put 10 mL of a mixture of standard solution of Cd (II), Cu (II), Pb (II) and Zn (II) 10 ug/L, added 0.2 mL and 0.2 mL of 0.1 M KCl kalkon in 20 ml, this variable is set constant during the experiment. Calkon concentration, pH, potential accumulation and time accumulation is set according to the experimental design of the Central Composite Design (CCD) in Table 1. From Table 1 is obtained peak current response of Cd, Cu, Pb and Zn ions.

Tabel 1: Optimization Cetral Composite Design (CCD)  for the

Simultaneous Determination of Cd, Cu, Pb, and Zn using calcon

Run	Factor				Peak current (nA)
	Calcon concentration (mM)	pH	Potential accumulation (V)	Time accumulation (s)	Cd	Cu	Pb	Zn
1	0.6	5	-0.7	40	21.75	129.74	52.22	57.58
2	0.6	5	-0.5	40	12.17	174.41	54.45	57.16
3	0.6	5	-0.7	80	37.35	178.61	105.90	43.44
4	0.6	5	-0.5	80	11.61	176.06	104.21	49.35
5	0.6	7	-0.7	40	16.36	266.66	40.21	87.60
6	0.6	7	-0.5	40	9.56	284.95	44.71	92.37
7	0.6	7	-0.7	80	23.61	269.02	38.17	77.73
8	0.6	7	-0.5	80	9.45	251.44	75.64	84.67
9	0.8	5	-0.7	40	25.11	180.35	41.40	61.13
10	0.8	5	-0.5	40	13.12	182.27	38.77	54.13
11	0.8	5	-0.7	80	48.71	191.26	79.17	54.13
12	0.8	5	-0.5	80	10.05	176.11	57.54	46.14
13	0.8	7	-0.7	40	92.35	295.00	39.16	83.35
14	0.8	7	-0.5	40	62.63	293.86	37.28	92.71
15	0.8	7	-0.7	80	101.69	313.50	40.20	90.03
16	0.8	7	-0.5	80	70.97	276.99	39.19	105.80
17	0.7	6	-0.6	60	104.33	221.07	80.86	101.49
18	0.7	6	-0.6	60	100.35	231.13	81.85	104.32
19	0.7	6	-0.6	60	105.21	232.14	80.86	105.29
20	0.7	6	-0.6	60	104.12	223.12	79.36	103.41
21	0.7	6	-0.6	60	103.13	222.07	83.14	103.43
22	0.7	6	-0.6	60	102.23	221.32	81.26	102.21
23	0.7	6	-0.6	60	104.12	222.04	81.26	101.21
24	0.532	6	-0.6	60	15.61	204.06	86.38	98.24
25	0.7	4.32	-0.6	60	19.67	201.89	74.87	92.89
26	0.7	6	-0.768	60	28.48	169.23	69.04	84.43
27	0.7	6	-0.6	26,4	12.25	123.32	33.70	88.11
28	0.868	6	-0.6	60	39.90	118.98	45.76	84.98
29	0.7	7.68	-0.6	60	78.77	117.77	69.87	97.65
30	0.7	6	-0.432	60	7.35	226.99	46.84	99.76
31	0.7	6	-0.6	93,6	12.72	186.71	87.97	83.61

 

Experimental design

The  CCD  system  is  an  effective  model  and  used  for  sequential experimentation which  provides information for testing ‘the goodness of fit’ and does not require unusual large number of design points thereby reducing the overall cost associated with the experiment. A four-factor central composite design (CCD) obtained by using Minitab 16 was  applied. The  four  factors considered to affect the peak current were calcon concentration, pH, potential accumulation and time accumulation. The level and ranges chosen for the factors are shown in Table 2.

Table 1 (a) : Level CCD variables for parameters independent (free) of a mixture of metal ions (Cd, Cu, Pb   and Zn)

Factor		Level  (Cd, Cu, Pb, Zn)
		–1	0	+1
Calcon concentration (mM)	C	0,6	0,7	0,8
pH	pH	5	6	7
Accumulation Potensial (V)	E	-0,7	-0,6	-0,5
Accumulation time (s)	T	40	60	80

 

Source  : level 0  diambil dari penelitian sebelumnya [1].

Sample Preparation

Vegetable samples were used in this study are: cauliflower, cabbage, eggplant and broccoli, while the fruit samples are used : apples, bananas kepok, melon and dragon fruit.

Vegetable and fruit samples before the specified metal content of Cd  are determined once the water content, then wet destruction with the addition of nitric acid and perchloric acid pa. Each sample weighed 0.5000 grams carefully dried and crushed, put in a flask digestion/kjeldahl flask. Furthermore, wet  destruction with the addition of 5 mL of concentrated nitric acid  and 0.5 mL of concentrated perchloric acid, shaked and left overnight. Onwards, heated at block digestor started with a temperature of 100^oC, after the yellow steam discharged elevated temperature up to 200 ^oC. Destruction ended when already out of white vapor and liquid in the flask remained about 0.5 mL, cooled and diluted with double destilation and matched into a 50 mL volume, shaken until homogeneous and left overnight and filtered with Whatman paper 41. The clear solution is ready determined metal content Cd with Voltammeter tools and Atomic Absorption Spectrophotometer. Determining the optimum conditions used in this study was the procedures that have been developed prior research team^1-2. The data processing is done with the help of software Minitab 16.

Results and  Discussion

Optimization  of  Cadmium Using One Variable.

The optimization of one  variable in the simultaneous determination of trace metal  cadmium  in the presence  of calcon has been done^1-3. The optimum condition as follow: calcon concentration  0.6 mM,  pH 6, accumulation potential -0.6 V,  accumulation time 60 seconds.  This technique does not describe the full effect on the response parameters and optimization of these factors is the increase in the number of trials required to do research, which leads to increased time and increased consumption of reagents and materials. Therefore to overcome this problem, an optimization technique of analytical procedures is by using Central Composite Design (CCD).

Optimization of Cadmium Using CCD

Analysis  of   CCD First-Order Model of Copper

The data processing was done  using  software Minitab 16, and the resuls can be seen in Table 2 the following :

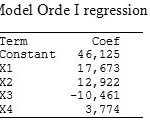Table 2: Model Orde I regression coefficient  Click here to View table

Based on Table 2,  regression equation of first-order model  was :

Ŷ = 46,125+17,673X1+12,922X₂-10,4610X₃+3,774X₄

Where X₁ = calcon concentration (µg/L),  X₂ = pH,   X₃ = accumulation potential (µg/L), X₄ = accumulation time (seconds), and  Ŷ = peak current (nA), whereas the results of  Analysis of Variance (ANOVA) of  first-order model   can be seen at  Table 3.

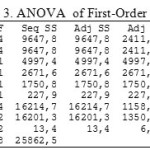Table 3: ANOVA  of First-Order Model of Copper   Click here to View table

 

Table 3 test procedure used to determine whether first-order models can be used or not. This hypothesis test was used to test the significance of regression models, which test whether there was a independent variable that significantly influence the response/dependent variable.

Ho:  βi = 0,

H1:  βi ≠ 0; i = 1,2,3,4

Based on Table 3, the test regression parameters simultaneously produce p-value of 0.138, meaning that the p-value is greater than the significance level used in the amount of α = 0.05. Thus it was decided not to reject Ho  and conclude that none of the independent variables that significantly influence the response variable, so the first-order model can not be used

Analysis CCD Second-Order Model of Copper

First-order model can not be used, then proceed with the second-order model by using a quadratic effect and interaction. Results of second-order model  data processing obtained (Table 4) the following results:

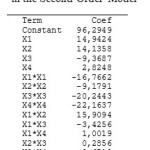Table 4: Regression Coefficients in the Second-Order Model Click here to View table

 

Based on Table 4, the model regression equation :

Ŷ = 96,2949+14,9424X₁+14,1358X₂-9,3687X₃+2,8248X₄-16,7662X₁²-9,1791X₂²-20,2443X₃²-22,1637X₄²+15,9094X₁X₂-3,4256X₁X₃ +1,0019X₁X₄+0,2856X₂X₃ -0,6719X₂X₄-3,1994X₃X₄

Where X₁ = calcon concentration (µg/L),  X₂ = pH,   X₃ = accumulation potential (µg/L),   X₄ = accumulation time (seconds), and Ŷ  = peak current (nA). Results of  ANOVA second-order model  data were presented in  Table 5.

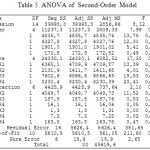Table 5: ANOVA of  Second-Order Model Click here to View table

Ho: βi = 0,

H1:  βi ≠ 0; i = 1,2,3, …, k

Based  on  Table  5  test  procedure against the  second-order model.  This  hypothesis test  was  used  to  test  the significance of regression models, which test whether there is a independent variable (including quadratic and interaction effects) significantly affects the response variable. Test regression parameters simultaneously produce p-value of 0.000, meaning that the p-value obtained is smaller than the significance level used in the amount of a = 0.05. Thus it was decided to reject Ho and conclude that there was a independent variable that significantly influence the response variable, so that the second-order model can be accepted.

Based on the regression coefficient values in Table 3 can be arranged matrix b and B as follows:

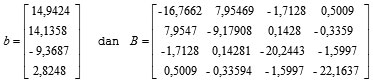
In order to obtain a stationary point as follows:

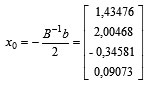
Thus, the solution in response to the stationary point is obtained as follows:

Furthermore, the stationary point can be restored to the true value, acquired conditions that provide the optimal solution (Table 6) was as follows:

Table 6: Optimal Value of cadmium

Variable	Optimal value   (with coding)	Optimal value (without coding)
X1	1,43476	0,8435
X2	2,00468	8,0047
X3	-0,34581	-0,6346
X4	0,09073	61,8146

 

Where X₁ = calcon concentration (µg/L),  X₂ = pH,   X₃ = accumulation potential (µg/L), and  X₄ = accumulation time (seconds). To get an idea of the characteristics of the surface of the response calculating eigen values ( λ) of the matrix B and obtained :

Because all four eigen values is negative, then the surface shape is the maximum response. It can be seen plot contour and response surface plot. By making constans two of the four factors were observed at a stationary point, then it may be possible to plot contour and response surface as shown in Figure 1.

Based on data analysis with CCD, it is concluded that the peak flow will reach its maximum value at the time of calcon concentration 0.8435 mM, pH 8.0047, accumulation potential -0.6346 Volt and accumulation time 81.85 seconds with a maximum peak current value of cadmium 61.8146 nA.

Contour and surface plot of  cadmium at stationary point By making constant two of the four factors used, then it can be shown that the shape and surface contour is the maximum response. The following will be presented contour plot and the surface on every possible pair of factors used.

Figure 1: Contour and surface plot of  cadmium Click here to View figure

 

Analysis of Real Samples

To evaluate the validity of the proposed method for real sample analysis, the proposed procedure was applied to various fruit  and  vegetable samples. The cadmium contents of  fruit and vegetable samples were determined by standard addition method using the recommended procedure under optimum conditions. The results in Tables 7 show that the method is good results with relative standard deviation of 0.84%, recovery 98.884%, the linear range up to 110 µg/L,  limit of detection 1.009 µg/L and LOQ  3.363 µg/L). Also, as it can be seen, the assay results for all the fruit and vegetable samples were in good agreement with the values that were obtained by standard atomic absorption spectroscopy.

Table 7 : Determination of Cd using  Adsorptive  stripping  voltammetry (AdSV)  and  Atomic absorption spectroscopy (AAS)

Sample	Cd (mg/L)
	AdSV	AAS
Broccoli (Brassica oleracea var. Italica)	3,340	0,926
Cauliflower (Brassica oleracea var. botrytis)	3,086	0,994
Eggplant (Salanim melongena)	2,357	1,080
Cabbage (Brassica juncea L)	5,761	1,126
Apple (Malus sieversii)	1,887	1.012
Banana kepok (Musa acuminata L)	6,591	0,824
Dragon fruit (Hylocereus undatus)	2,671	0,936
Melon (Cucumis melo L)	4,318	0,839

 

Conclusion

Based on data analysis with  central composite design, the simultaneous determination of cadmium obtained optimum conditions, namely: calcon concentration 0.8435 mM, pH 8.0047, accumulation potential -0.6346 Volt and accumulation time 81.85 seconds with a maximum peak current value of cadmium 61.8146 nA. The method has a very excellent  with relative standard deviation of 0.84%, recovery 98.884%, the linear range up to 110 µg/L,  limit of detection 1.009 µg/L and LOQ  3.363 µg/L. The central composite design can be applied to the determination of cadmium in fruit and vegetable samples quickly, effectively and efficiently.

Acknowlegment

The author would like to thank  to Ministry of  Research, Technology dan Higher Education, which has funded this study, in accordance with the Agreement on Implementation of Research Grant 2016.

References

1. Deswati;  Suyani, H. and Safni. Indo. J. Chem. 2012, 12(1) : 20 -27
2. Deswati;  Suyani, H; Safni;  Loekman, U and Pardi,H.  Indo. J. Chem.2013, 13(3) : 236-           241.
3. Deswati; Amelia, L; Suyani, H; Zein, R and Jin, J. Rasayan. J. Chem. 2015, 8(3) : 362- 372.
4. Deswati;  Munaf, E; Suyani, H; Loekman, U and Pardi,H. Res. J. Pharm, Biol. Chem. Sci. 2014, 5(4): 990-999.
5. Gholivand, M.B; Sohrabi, A and Abbasai, S.    Electroanalysis. 2007, 19,  319-322.
6. Deswati;  Munaf, E; Suyani, H; Zein, R and Pardi, H. Asian J. Chem. 2015, 27(11) : 3978- 3982.
7. Bezerra, M.A; Santelli, R.E; Oliveir, E.P; Villar, L.S and Escaleira, L.A. Talanta. 2008, 76 : 965 – 977.
   CrossRef
8. Deswati; Rahmi HG, I; Suyani, H; Zein, R and Alif, A. Rasayan J. Chem.  2016, 9(1) : 8-17
9. Rahmi HG, I; Deswati; Suyani, H and Zein, R. Res. J. Pharm, Biol. Chem. Sci. 2016, 7(3): 673-682
10. Deswati;  Suyani, H; Zein, R and Rahmi,I.  J. Chem. and Parm Res. 2015,  7(8) : 750-757.
11. Oramahi, H.A.Theory and aplication of Respon Surface Methodology, Publisher Ardana Media, Yogyakarta. 2008, 6 -12.
12. Ensafi, A.A; Abbasiand, S and Mansour, H.R. Anal. Sci. 2001, 17 : 609-612
    CrossRef
13. Paolicchi, I; Renedo, O.D; Lomillo, M.A.L and Martinez, M.A.A. Anal. Chem. Acta. 2004, 511: 223 – 229
    CrossRef
14. Dewi, A.K; Sumarjaya, I.W and Srinadi, I.G.A.M.  E-Journal of Math. 2013, 2(2) : 32-36.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.