Kinetics and Mechanism Investigation on Green and Three –Component One Spot Synthesis of 4H-Tetrahydrobenzo[B]Pyrans using Caffeine as A Facile and Green Catalyst

Introduction

In recent times, the development of environmentally benign and clean synthetic procedures has become the goal of organic synthesis ^1,2. The use of water and ethanol as a reaction medium exhibits a remarkable benefit because of its highly polarity and therefore immiscibility with the most organic compounds. Tetrahydrobenzo[b]pyrans are an important class of heterocyclic scaffolds in the field of drugs and pharmaceuticals. These compounds are widely used as anti-coagulant, diuretic, spasmolytic, anticancer and anti-anaphylactic agents ^3–5.

The simplest method involves one-pot, three-component condensation of malononitrile, an aldehyde and dimedone in different conditions ^3,6–14. Various catalysts ¹⁵ such as Na₂SeO₄, hexadecyldimethylbenzyl ammonium bromide ^16, NaBr ¹⁷, tetramethyl ammonium hydroxide (CH₃)₄ N⁺OH^–, ¹⁸ TEBA, ¹⁹ KF-montmorillonite ²⁰, KF-alumina ²¹, organocatalysts ²², acetic acid ²³, diammonium hydrogen phosphate ²⁴ and hexadecyltrimethyl ammonium bromide ²⁵ have been used in this synthesis.

However, most of the methods to prepare 4H-benzo[b]pyran suffer from certain drawbacks including long reaction times, unsatisfactory yields, higher temperatures and use of expensive non reusable catalyst. To avoid these limitations, the discovery of a mild and efficient catalyst with high catalytic activity, short reaction time, simple work-up procedure and recyclability of catalyst is still being actively pursued for the synthesis of 4H-benzo[b]pyrans ^26-36.

We focused our investigation to developing new synthetic methods for the preparation of tetrahydrobenzo[b]pyran using benzaldehydes 1, malononitrile 2 and dimedonein 3 in the presence of caffeine as catalyst in a mixture of (ethanol / water, 1:2 ) (Fig. 1).

Kinetic analysis often used to be studied to see what happens to the molecular level during a chemical reaction. In a kinetic study of an organic reaction, for instance, experimental results in confirm or rejection to a proposed mechanism may have compelled us to think of a more detailed chemical reaction. The purpose of any kinetic study is to form a quantitative relationship between the rate of a reaction and the concentration of reagents or catalysts [37]. Thus, the best solution to meet this aim is simply to follow the disappearance of the starting material or appearance of a product as a function of time. This can be done by measuring the rate of a reaction at various concentrations of reactants and catalysts in order to determine the kinetic order with respect to a particular reactant and to establish an overall function which represents the rate law of a behavior reaction with a known rate constant. Kinetics studies suggest many practical techniques to accomplish these measurements. The literature, experimental and theoretical kinetics studies and mechanism investigation have fully been discussed for various reactions such as ylides [38–50]. Herein, we were interested in studying the kinetics of the reaction and the details of our findings are reported in this paper, comprehensively.

 

Figure 1: Synthesis of tetrahydrobenzo[b]pyran in the presence of caffeine in a mixture of (water/ethanol, 2:1). Click here to View figure

Experimental

Chemicals and Apparatus used

All reagents and solvent were purchased from Merk and Aldrich and used without any purification. Rate constants are presented as an average of several kinetic runs (at least 6-10) and are reproducible within ± 3%. The overall rate of reaction is followed by monitoring absorbance changes of the products with time on a Varian (Model Cary Bio-300) UV-vis spectrophotometer with a 10 mm light-path cell. Temperature of the reaction is maintained to within ±0.1 °C at various temperatures by circulating water a mixture of water at ethylenglycol bath.

 Kinetics

To achieve more information about the mechanism of synthesizing of tetrahydrobenzo[b]pyrans, a kinetics study of the reaction between benzaldehyde 1, malononitrile 2 and dimedone 3 in the presence of caffeine in a mixture of (water/ethanol, 2:1) was undertaken by UV-vis spectrophotometry technique. Firstly, it is essential to find an appropriate wavelength in order to follow the kinetic study of the reaction. In this regard, in the first experiment, 10^-2 M solution of each reactant 1, 2, 3 and 2×10^-3 M solution of caffeine were prepared in a mixture of a mixture of (water/ethanol, 2:1) as solvent. Approximately 3 mL aliquot from each reactant was pipetted into a 10 mL light path quartz spectrophotometer cell and the relevant spectrum of each compound at 25°C was recorded over the wavelength range 200-600 nm. In the second experiment, 0.2 mL aliquot of 8×10^-3 M solution of caffeine and 0.2 mL aliquot of 4×10^-2 M solution of reactants 1 and 3 were pipetted into a quartz spectrophotometer cell, then 0.2 mL aliquot of 4×10^-2 M solution of reactant 2 was added to the mixture according to stoichiometry of each reactant in the overall reaction. The reaction was monitored by recording scans of the entire spectra with 20 minute intervals during the whole reaction time at the ambient temperature (Fig. 2). As can be seen in Fig. 2, the appropriate wavelength was detected to be 385 nm (corresponding mainly to the product 4). Since at this wavelength, reactants 1, 2, 3 and caffeine have relatively no absorbance value, it gave us the chance to find the practical conditions that allows kinetics and a mechanistic investigation of the reaction. It’s important to note that, the concentration range was measured over (10^-4M ≤ M product ≤10^-2M) to prove a linear relationship between the absorbance and concentrations values.

In the third experiment, under the same concentration (10^-2 M) of 1, 2 and 3 in the presence of caffeine (2×10^-3 M) in a mixture of (water/ethanol, 2:1) at 25℃, the reaction kinetics was followed by indicating the UV absorbance measurements as a function of time (Fig. 2.).

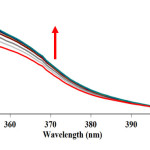Figure 2: The UV-vis spectra of the reaction between benzaldehyde 1 (10-2M), malononitrile 2 (10-2 M) and dimedone 3 (10-2M) in the presence of caffeine (2×10-3 M) as a catalyst in a mixture of (water/ethanol, 2:1) as reaction proceeds into a 10 mm light-path cell. Herein, the upward of direction of the arrow indicate that the progress of product versus times. Click here to View figure

 

The infinity absorbance (A_∞) was sampled every 2 minutes for an overall time span of 20 minutes as reported in Fig. 3. With respect to this value, zero, first or second curve fitting could be drawn automatically for the reaction by the software associated [51] with the UV instrument. A second order fit curve (solid line) was obtained from the absorbance data versus time provided at 380 nm that precisely described the experimental curve (dotted line) as reported in Fig. 3. It is obvious that the reaction is second order. Thus, overall order of reaction is α + β + γ = 2. Therefore the second-order can be reported (k_over = 7.93 min^-1.M^-1)

In this case, rate law can be written as:

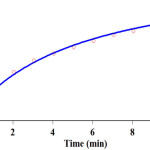Figure 3: The experimental absorbance change (dotted line) along with the fit curve (solid line) against time for the reaction between benzaldehyde 1 (10-2 M), malononitrile 2 (10-2 M), and dimedone 3 (10-2 M) in the presence of caffeine (2×10-3 M) in a mixture of (water/ethanol, 2:1) at 380 nm and 35.0°C  Click here to View figure

Effect of Solvents and Temperature

Temperature and the solvent environment has their effects on the rate of reaction so, both of them were investigated through various experiments under different conditions of temperatures and the solvents, but, under the same condition as the earlier experiments.

Because the transition state (Step 1, Fig. 9) in reaction carries a dispersed charge, solvents with higher dielectric constant speed up reaction rate (Table 1) by stabilizing the species at the transition state more than reactants, and therefore E_a would be made lower.

 Table 1 : k_obs (M^-2min^-1) for the reaction between 1 (10^-2 M), 2 (10^-2M) and 3 (10^-2 M) and caffeine (2×10^-3 M) in different solvent media and temperatures.

^a: dielectric constant (D)

^b: standard deviation (SD).

In the investigation range of the temperature, the relation of the second order rate constant (ln k₁) of the reactions on reciprocal temperature confirms Arrhenius equation. This manner is indicated in (Fig. 4). The activation energy, for the reaction between 1, 2 and 3 was acquired forming the slope of (Fig. 4).

On the basis of Eyring equations (2) and (3) the activation parameters H^‡ (activation enthalpy) and S^‡ (activation entropy) were determined using the intercept and slope, respectively (Figs 5 and 6).

That k_B is Boltzmann’s constant, T is temperature, h is Planck’s constant and R is universal gas constant.

From the Eyring equation it is concluded that the standard errors of ΔS^‡ and ΔH^‡ correlate as the following equation:

 

 

Where T_av is the center of the temperature range used in this experiment. It follows that in most solution phase studies σ ( ≈  × 0.003 K^-1. This correlation has been mentioned elsewhere [52-54]. The standard errors for activation parameters have been calculated and they have been reported along with these parameters in both Table 2.

Furthermore, ΔG^‡ (Gibbs free energy) was determined using the equation (5):

According to equation (22), k₁ is proportional to the general reaction rate, hence, the activation parameters which include ΔG^‡, ΔS^‡ and ΔH^‡ can now be computed for the first step (rate determining step, k₁), as an elementary reaction. Obtained activation parameters for two solvents are given in Table 2.

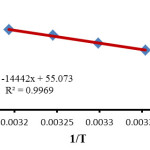Figure 4: The dependence of the second order rate constant (lnk) on reciprocal temperature for the reaction between 1, 2 and 3 in the presence of caffeine measured at a wavelength of 380 nm in a mixture of (water/ethanol, 2:1), according to the Arrhenius equation. Click here to View figure

 

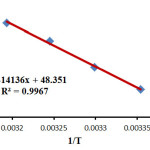Figure 5: Eyring plots according to equation (2) for the reaction between 1, 2 and 3 in the presence of caffeine in a mixture of (water/ethanol, 2:1).  Click here to View figure

 

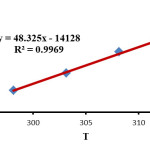Figure 6: Eyring plots in accordance with equation (3) for the reaction between 1, 2 and 3 in the presence of caffeine in a mixture of (water/ethanol, 2:1).  Click here to View figure

 

Table 2: Activation parameters for the reaction between compounds 1, 2, 3 and caffeine measured in different solvent media.

solvent	DHǂ ( kJ mol-1 )	DSǂ ( Jmol-1 )	DGǂ ( kJ mol-1 )	Ea ( kJ ⁄ mol )
water/ethanol (2:1) (58.6)a	117.46 ± 1.61	204.23 ± 5.29	56.56 ± 3.19	119.93 ± 1.61b	120.07 ± 1.61c
ethanol (24.3)a	153.45 ± 2.31	311.87 ± 7.55	60.47 ± 4.56	155.84 ± 2.31b	155.93 ± 2.31

a: dielectric constant (D)

b: according to this equation: Ea = DHǂ + RT

c: in accord with the Arrhenius equation

It’s understood from the high value of E_a that the reactant is in need of higher amount of energy to increase its temperature to transition state. The value of activation enthalpy (DH^ǂ) and free energy of activation (DG^ǂ) are positive and have rather large values which suggest that the energy required for the reaction is relatively high. A positive value for entropy of activation DS^ǂindicates that the transition state is highly disordered compared to the ground state. Looking at detail, the activation enthalpy is lower in solvent with high dielectric constant (water/ethanol, 2:1) with respect to lower dielectric constant (ethanol) at same temperature, and this give rise to lower activation energy for reaction in solvent with high dielectric constant because E_a is directly proportional to the activation enthalpy( E_a = DH^ǂ + RT). Moreover, the positive value of DG^ǂis a sign for the reaction to be spontaneous.

Effect of concentration

Obviously, concenteration factor plays an important role in kinetical study, spetially for finding partial order of reactant 3 under pseudo-order condition, in a separate experiment (fourth experiment), same procedure was employed with these concentrations [(10^-2 M, reactant 1), (10^-2 M, reactant 2)], [(5×10^{-3 M, reactant 3)] and caffeine (2×10-3} M). For obtaining equation (6), the rate law can be expressed:

 

In this work, the original experimental absorbance versus time data reported a second-order behavior as a function of time. This is demonstrated as the full line at 380 nm that is roughly coincident with the experimental result (Fig. 7).additionally, The observed rate constant (k_obs) was automatically calculated by the software associated with UV/vis instrument (k_obs=7.80)

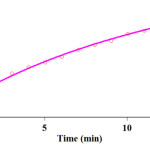Figure 7: Pseudo-second order fit curve (solid line) along with the original experimental curved (dotted) for the reaction between dimedone 3 (5×10-3 M), malononitrile 2 (10-2 M) and benzaldehyde 1 (10-2 M) in the presence of caffeine (2×10-3 M) at 380 nm and 35.0°C in a mixture of (water/ethanol, 2:1). Click here to View figure

 

Fig. 7. Pseudo-second order fit curve (solid line) along with the original experimental curved (dotted) for the reaction between dimedone 3 (5×10^-3 M), malononitrile 2 (10^-2 M) and benzaldehyde 1 (10^-2 M) in the presence of caffeine (2×10^-3 M) at 380 nm and 35.0°C in a mixture of (water/ethanol, 2:1).

The experimental data displayed that the observed pseudo-second order rate constant (k_obs = 7.80, fourth experiment, pseudo-order condition) is identical with second order rate constant, (k_obs = 7.93, secend experiment) which implies that probably γ = 0 in equation (6).

In the fifth experiment, for evaluating a partial order of reaction in relevant to benzaldehyde 1, pseudo-order condition was defined for the reaction between the 2 (10^-2 M), 3 (10^-2 M) and 1 (5×10^{-3 M) in the presence of caffeine (2×10-3} M) in a mixture of (water/ethanol, 2:1). According to the fifth experiment, the rate law can be expressed as:

The original experimental absorbance versus time (full line) at 380 nm well fits the experimental data (circles), shown in Fig. 8.

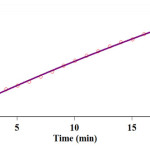Figure 8: Pseudo- First order fit curve (solid line) accompanied by the original experimental curve (dotted line) for the reaction between 1 (10-3 M), 2 (10-2 M) and 3 (10-2 M) in the presence of caffeine (2×10-3 M) at 380 nm and 35.0°C in a mixture of (water/ethanol, 2:1). Click here to View figure

 

Fig. 8. Pseudo- First order fit curve (solid line) accompanied by the original experimental curve (dotted line) for the reaction between 1 (10^-3 M), 2 (10^-2 M) and 3 (10^-2 M) in the presence of caffeine (2×10^-3 M) at 380 nm and 35.0°C in a mixture of (water/ethanol, 2:1).

From Fig. 8, it is sensible to say that the partial order of reactant 1 with respect to equation 3 is one (a = 1). As results of UV/vis experiments have shown, α + β + γ = 2 from the third experiment so that, γ is found to be zero from the fourth experiment. Then, the value of α = 1 is calculated in fifth experiment, finally, this parameters lead to β = 1 in the whole UV/vis experiments. So the rate law can be expressed as:

To investigate which steps of the proposed mechanism is a rate-determining step, the rate law was written using the final step of reaction:

The steady-state approximation can be employed for [I₁] that yields the equation (10) in the following:

 

The value of [I₄] can be replaced in equation (9) to attain this equation:

For attaining the intermediate concentration [I₃] the following equation is yielded by applying the steady state approximation:

By substituting equation (13) in (12) and some straight forward math the following equation is emerged:

The steady state approximation can then be applied for attaining the concentration of [I₂] which is represented in the following formula:

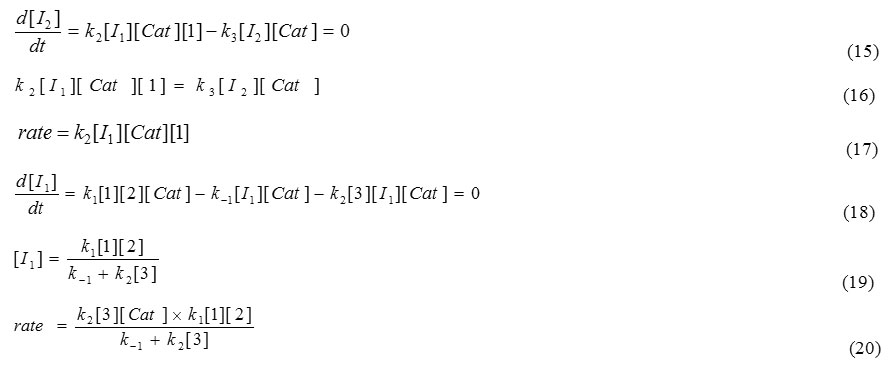
k₄, k₅ and k₃ are not attained in equation (20), therefore this rate constants have no chance to be a rate determining step, but step 1 (k₁) and step 2 (k₂) have a good opportunity to be a rate determining step.

If k₂ is rate determining step, so the following speculation is reasonable: k₂ [3] << k_-1

The new equation can be presented:

This equation is not compatible with the experimental rate law (equation 4), because the presented equation (21) is a third-order reaction with respect to compounds 1, 2 and 3, while the obtained results from the UV experiments indicate that overall order of reaction is two.

If k₁ is a rate determining step, the following assumption is logical: k₂ [3]  >> k_-1

So the new generation of the rate law can be expressed:

 

The last equation (22) is the same as the rate law that obtained from the UV experiment (equation 4). It is obvious that the original order of the reaction is two. In addition, the order of the reaction with respect to each reactant (1, 2 and 3) is 1, 1 and zero, respectively. Also, because of the presence of k₁ in the rate law (22), it becomes clear that the first step (k₁) is a rate determining step.

Utilizing the above results a speculative mechanism containing five steps to be proposed in accord with knoevenagal condensation between benzaldehyde 1, malononitrile 2, for generation of 2-benzylidenemalononitrile I₁, Michael addition of I₁ with dimedone 3 producted I₂ which subsequently followed tautomerization and cyclization afforded the corresponding product 4 (Fig. 9).

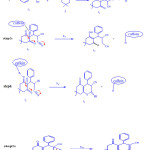Figure 9: A proposed mechanism of the reaction between 1, 2 and 3 in the presence of caffeine for synthesis of 2-amino-5,6,7,8-tetrahydro-7,7-dimthyl-4-(phenyl)-5-oxo-4H-chromene-3-carbonitrile 4 in a mixture of (water/ethanol, 2:1). Click here to View figure

Fig. 9. A proposed mechanism of the reaction between 1, 2 and 3 in the presence of caffeine for synthesis of 2-amino-5,6,7,8-tetrahydro-7,7-dimthyl-4-(phenyl)-5-oxo-4H-chromene-3-carbonitrile 4 in a mixture of (water/ethanol, 2:1).

A simplified scheme of the proposed reaction mechanism (Fig. 9) is shown in Fig. 10.

Fig.10. A simplified Scheme for the proposed reaction mechanism

Figure 10: A simplified Scheme for the proposed reaction mechanism Click here to View figure

Conclusion

In summary, kinetic investigation of later reactions was done using UV spectrophotometry and the results are declared in the following terms. The overall order of reaction for the formation of a 4H-tetrahydrobenzo[b]pyran in the presence of caffeine followed second-order kinetics. The partial orders with respect to benzaldehyde 1, malononitrile 2 and dimedone 3 were one, one and zero, respectively. It is understood from the result that the rate of reaction speeds up in a solvent with high dielectric constant (water/ethanol, 2:1) in comparison to those with lower dielectric constant (ethanol) at all temperatures. In the studied temperature range, the second-order rate constant of the reaction was inversely proportional to the temperature, which was in agreement with the Arrhenius equation. From the temperature and solvent studies, the activation energy (E_a) and the related kinetic parameters (ΔG^‡, ΔS^‡ and ΔH^‡) are calculated. It’s obvious that the large positive value of activation parameters leads to a stiff reaction progress. Therefore, the first step of proposed mechanism was identified as a rate-determining step (k₁) and this was confirmed based on the steady-state approximation.

Acknowledgement

Authors sincerely thank Sistan and Baluchestan University for providing the financial support of this work.

References

1. Grieco, P. A. Organic Synthesis in water. Thomson Science, London, 1998.
   CrossRef
2. Li, C. J. Chem Rev. 2005, 105, 3095.
   CrossRef
3. Andreani, L. L.; Lapi, E. Boll. Chim Farm. 1960, 99, 583.
4. Singh, K.; Singh, J.; Singh, H. Tetrahedron. 1996, 52, 14273.
   CrossRef
5. Bonsignore, L.; Loy, G.; Secci, D.; Calignano, A. Eur. J Med Chem. 1983, 28, 517.
   CrossRef
6. Wang, X. S.; Shi, D. Q.; Tu, S. T.; Yao, C. S. Synth Commun. 2003, 33, 119.
   CrossRef
7. Tu,S. J.; Gao,Y.; Guo, C.; Shi, D.; Lu, Z. Synth Commun. 2002, 32, 2137.
   CrossRef
8. Li, J. T.; Xu, W. Z.; Yang, L. C.; Li,T. S. Synth Commun. 2004, 34, 4565.
   CrossRef
9. Jin,T. S.; Wang, A. Q.; Wang, X.; Zhang, J. S.; Li, T. S. Synlett. 2004, 11, 871.
   CrossRef
10. Shi,D. Q.; Zhang, S.; Zhuang,Q. Y.; Tu, S. J.; Hu, H. W. Chin. J Org Chem. 2003, 23, 877.
11. Penjg, Y.; Song, G. Catal Commun. 2007, 8, 111.
    CrossRef
12. Hekmatshoar, R.; Mojedi, S.; Bakhtiari, Kh. Catal Commun. 2008, 9, 307
    CrossRef
13. Balalaie, S.; Sheikh-Ahmadi, M.; Bararjanian, M. Catal Commun. 2007, 8, 1724.
    CrossRef
14. Lian,X. Z.; Huang, Y.; Li, Y. Q.; Zheng, W. J. Monatsh. 2008, 139, 129.
    CrossRef
15. Hekmatshoar, R.; Majedi, S.; Bakhtiari, K. Catal Commun. 2008, 9, 307.
    CrossRef
16. Jin, T. S.; Wang, A. Q.; Shi,F.; Han, L. S.; Liu, L. B.; Li, T. S. ARKIVOC. 2006, 78.
17. Devi, I.; Bhuyan, P. J. Tetrahedron Lett. 2004, 45, 8625.
    CrossRef
18. Balalaie, S.; Sheikh-Ahmadi, M.; Bararjanian, M. Catal Commun. 2007, 8, 1724.
    CrossRef
19. Rong, L.;Li, X.;Wang, H.;Shi, D.;Tu, S.;Zhuang, Q. Synth Commun. 2006, 36, 2363.
    CrossRef
20. Zhuang, Q. Y.; Wu, N.; Shi, D. Q.; Tu, S. J.; Wang, X. S. Chin J Org Chem. 2006, 26, 1217.
21. Wang, X S.; Shi, D Q.; Tu, S J and Yao,C S. Synth Commun. 2003, 33, 119.
    CrossRef
22. Lian, X. Z.; Huang, Y.; Li, Y. Q.; Zheng, W. J. Monatshefte fur Chemie. 2008, 139, 129.
    CrossRef
23. Kamaljit, S.; Jasbir, S.; Harjit, S. Tetrahedron. 1996, 52, 14273.
    CrossRef
24. Balalaie, S.; Bararjanian, M.; Sheikh-Ahmadi, M.; Hekmat, S.; Salehi, P. Synth Commun. 2007, 37, 1097.
    CrossRef
25. Gao,S.; Tsai, C. H.;Tseng C and Yao, C. F. Tetrahedron. 2008, 64, 9143.
    CrossRef
26. Parveen, A.; Ahmed, M. R. S.; Shaikh, K. A.; Deshmukh, S. P.; Pawar, R. P. ARKIVOC. 2007, 16, 12.
27. Breck, D. W. Zeolite Molecular Sieves, Wiley, New York, 1974.
28. Ramesh, K.; Karnakar, K.; Satish, G.; Nageswar, Y. V. D. Chin Chem Lett. 2012, 23, 1331.
    CrossRef
29. Hazeri,N.; Maghsoodlou, M. T.; Mir, F.; Kangani, M.; Saravani, H.; Mollashahi, E. Chin J Catal. 2014. 35(3), 391-395.
    CrossRef
30. Grieco, P. A. (Ed.), Blackie, London, 1998.
31. Shinde, S.;Rashinkar, G.; Salunkhe, R. Journal of Molecular Liquids, 2013, 178, 122.
    CrossRef
32. Hazeri, N.; Sajadikhah, S. S.; Maghsoodlou, M. T. J Chem Res, 2013, 37, 550.
    CrossRef
33. Kangani, M.; Hazeri, N.; Maghsoodlou, M.; Salahi, S. Res Chem Intermed. 2013, 23, 2365-2369.
34. Mousavi,M. R.; Hazeri, N.; Maghsoodlou, M. T.; Salahi, S.; Habibi-Khorassani, S. M. Chin Chem Lett. 2013, 24, 411.
    CrossRef
35. Mousavi, M. R.; Aboonajmi, J.; Maghsoodlou, M. T.; Hazeri, N.; Habibi-Khorassani ,S. M.; Safarzaei, M. Lett Org Chem. 2013, 10, 171.
    CrossRef
36. Noorisadeh, F.; Maghsoodlou, M.T.; Hazeri, N.; Kangani,M. Res Chem Intermed. 2014, 29, 236-239.
37. Carey, F. A.; Sundberg, R. J. Kluwer Academic Press, New York, 2000.
38. Shaharaki, M.; Habibi-Khorassani, S. M.; Ebrahimi, A.; Maghsoodlou, M. T.; Paknahad, A. Prog React Kinet Mech, 2009, 37, 321.
    CrossRef
39. Shahraki, M.; Habibi-Khorassani, S. M.; Dehdab, M. RSC Adv. 2015, 5(65), 52508-52515.
    CrossRef
40. Shahraki, M.; Habibi‐Khorassani, S. M. J Phys Org Chem. 2015, 28 (6), 396-402.
    CrossRef
41. Dehdab, M.; Habibi-Khorassani, S.; Shahraki, M., Catal Lett. 2014, 144(11), 1790-1796.
    CrossRef
42. Habibi-Khorassani S. M.; Shahraki, M.; Dehdab, M.; Poorshamsoddin, M. A. J Solution Chem. 2015, 44, 2154.
    CrossRef
43. Pourpanah, S. S.; Habibi-Khorassani, S. M.; Shahraki, M. Chinese J Catal. 2015, 36(5), 757-763.
    CrossRef
44. Habibi-Khorassani, S. M.; Maghsoodlou, M. T.; Ebrahimi, A.; Zakarianejad, M.; Mohammadzadeh, P.; Shahraki, M. Int J Chem Sci. 2008, 6, 647.
45. Khorassani, S. M.; Ebrahimi., A.; Maghsoodlou, M. T.; Shahraki, M.; Price, D. Analyst. 2011, 136(8), 1713-1721.
46. Habibi-Khorassani, S.M.; Maghsoodlou, M.T.; Shahraki, M.; Poorshamsoddin, M.A.; Karima, M.; Abbasi ,M. Iranian journal of Catalysis. 2015, 5, 79-87.
47. Habibi-Khorassani, S.M.; Maghsoodlou, M.T.; Shahraki, M.; Hashemi-Shahri, M.; Aboonajmi, J.; Zarei, T. Iranian journal of Catalysis. 2015, 4, 241-246.
48. Habibi-Khorassani, S.H.; Maghsoodlou M., Ebrahimi A., Zakarianejad, M.; Mohammadzadeh, P.; Shahraki, M. Orient J Chem. 2008, 24, 73.
49. Yaghoubian, H.; Habibi-Khorassani, S.M.; Ebrahimi, A. Orient J Chemistry, 2015, 31(4), 2107-2113.
50. Yogananth, A.; Sheik Mansoor, S. Orient J Chem. 2015, 31(1), 17-23.
51. Schwartz, L. m.; Gelb, R. I. Anal. Chem. 1978, 50, 1592.
    CrossRef
52. Lente, G.; Fabian, I.; Poe, A. J. New J Chem. 2005, 29, 759.
    CrossRef
53. Espenson, J. H. McGraw-Hill, New York, 1995.
54. Poe, A. J.; Twigg, M. V. Plenum Prss, New York.1994.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.