Three-dimensional free vibration analysis of carbon nanotube reinforced composites annular plates

Introduction

In recent years astonishing advances in science and technology have motivated researchers to work on new structural materials possessing high strength to weight ratio. Carbon nanotube (CNT) reinforced polymer composites are one of these advanced materials, having many attractive applications in mechanical, chemical, electrical, optical, aeronautics, astronautics, and biomechanical industries.

A review of existing literature on the mechanical properties of CNT reinforced polymer composites demonstrates that many studies have been done recently e.g., ^1–11. Significant improvements in mechanical properties of polymeric matrixes have been reported by adding a few weight-percents (wt%) of CNTs.

Although a lot of parameters such as dispersion methods, type of CNTs, weight percentage of CNTs relative to matrix, etc., can affect the mechanical properties of composites; all in all it has been quite evident that added stiffness versus added mass unit is undeniably exceptional, which is very interesting for free vibration analysis. Technically speaking, composites annular plates are widely used in industrial structural elements. There are large number of research papers and reviews on the free vibration analyses of isotropic annular plates ^12-19. A few researchers have analyzed vibration and static behavior of nanocomposites plates ^20-23.

During the last decade, several research groups have presented theoretical models to predict mechanical properties of CNT reinforced polymer composites. An excellent survey of the research work on the different modeling techniques as proposed for predicting the mechanical behavior of polymer composites has been published by Valavala and Odegard ²⁴. The micromechanical model is one of the renowned methods extensively used to predict elastic properties of CNT/polyimide composites in lot of articles ^25-28. Mechanical properties of high density polyethylene composites reinforced with CNTs were presented by Kanagaraj et al. ²⁹. They employed both the Halpin-Tsai model and a modified form of the rule of mixture model to make a comparison between theoretical and experimental results. Bokobza ³⁰ used the Guth and the Halpin-Tsai predictions to compare her experimental values obtained for the Young’s modulus of MWCNTs/elastomeric composites with those predicted by the models. All proposed models (e.g. micromechanical, Halpin-Tsai and rule of mixture) used, for instance, in refs ^25-30, are valid only for low wt% of CNTs, where the variation of the Young’s modulus of CNT/polymer composites versus wt% of CNTs is almost linear. However, it is well known that there exists a nonlinear relationship between mechanical properties of CNT/polymer composites and volume fraction of CNTs. According to a comprehensive survey of literature, various authors have found that relatively little work is available on new micromechanics models, enabling us to properly predict the mechanical properties of CNT/polymer composites for both low and high wt% of CNTs. M. Omidi et al. ³¹ investigated the effect of MWCNT content on the mechanical properties of epoxy composites. They modified the rule of mixture model by introducing a length efficiency parameter, orientation efficiency factor and waviness parameter to the model. This model predicted the mechanical properties of nanocomposites for both low and high wt% of CNTs.

In this paper, a three-dimensional (3-D) free vibration analysis of CNT-reinforced composite annular plates with different combinations of boundary conditions at the inner and outer edges of the annular plate is presented on the basis of the Chebyshev-Ritz method. In order to achieve more reliable and precise results, the mechanical properties of the nanocomposites were obtained through a modified rule of mixtures theory ³¹. The validity and the range of applicability of the results obtained based on the other well-known theories (such as: Micro-Mechanical, Halpin Tesai and etc.) were studied by comparing them with those obtained by the modified rule of mixtures. Moreover, the influence of the CNT type (single wall or multi wall), structures (zigzag or armchair), diameter, shape factor, density and volume fraction on the frequency parameters of the plate was also studied.

Theoretical formulation

Consider a thick composite annular plate with outer radius, inner radius and thicknesses as depicted in Fig. 1. The plate geometry and dimensions were defined in an orthogonal cylindrical co-ordinate system (r,θ,z).

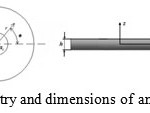Figure 1: Geometry and dimensions of an annular plate  Click here to View figure

 

Theory of fiber reinforced composite materials

Micromechanical Mori–Tanaka equations

A rather simple and accurate micromechanics method is Mori–Tanaka method ³². It assumes each inclusion in the infinite pristine matrix loaded by an effective stress that equals the average stress over the matrix. The effective moduli of inclusion-dispersed composites may be easily derived with good accuracy even for a high volume fraction of inclusions. For a composite reinforced by nanoparticles, this method leads to the effective Young’s modulus E_c, bulk modulus K_c and shear modulus G_c as:

 

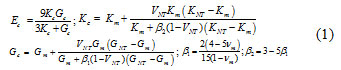
where  υ_m  the Poisson’s ratio of the matrix and, K and G denote the bulk modulus and the shear modulus, the subscripts ‘‘m” and ‘‘NT” stand for matrix and nanoparticulate, respectively.

The Halpin-Tsai equations

One of the equations which is frequently used for modeling the mechanical behavior of nanocomposites is the Halpin-Tsai equation which can be written as equation (2).

 

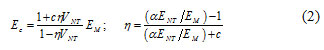
In which c=2(l/d) is a constant shape factor related to the aspect ratio of the reinforcement length l and diameter d. Also, E_M , E_NT , and V_NT are the modulii of matrix, CNT, and the volume fraction of nanotubes, respectively. Parameter α is an orientation factor which was later introduced by Cox ³³. For the random oriented in two dimensions α =1/3, and for the random oriented in three dimensions α =1/6.

The rule of mixtures equations

For a composite with uniaxial reinforcement and under constant strain conditions, the dependence of the elastic modulus on the long fiber like CNTs volume fraction can be estimated by the rule-of-mixture as follows:

E_c/M= (_K∫E_NT/M^-1) V_NT, (3)

Where E_C|_M= (E_c-E_M)| and E_NT|M =E_NT|E_M- takes a value between 0 and 1, and can be determined by:

 

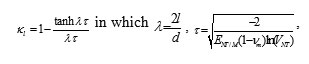
where λ is the CNT aspect ratio. The parameter  approaches 1 for large volume fractions of high aspect ratio CNTs.

The modified rule of mixtures theory

According to the experimental data reported in the literature ^31-40, when the volume fraction of CNTs takes larger values a nonlinear trend for the elastic modulus can be seen. As a consequence, the new form of the rule of mixtures can be expressed as

 

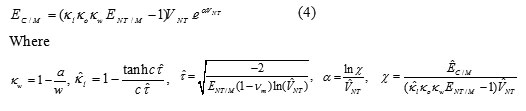
and È_C|M = (È_c– E_M)/E_M. Note that each parameter having the hat ^ should experimentally be determined by a tensile test for a given wt% of CNTs. In other words, the value of the parameter α is determined by testing only one tensile CNT composite specimen ³¹.

Energy and frequency equations

The constituent equation for the circular plate is:

[σ]= {S}[ε]   (5)

Where σ, S, and ε represent the stress tensor, compliance tensor, and strain tensor, respectively. Eq. 5 shows the relationship between stress and strain.

For free vibrations, the displacement components of a three-dimensional elastic body may be expressed as:

 

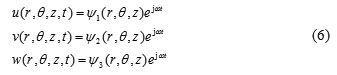
Where t is the time, ω denotes the natural frequency of vibration and j= √-1. Also, u, v, and w are referred to displacement components along the radial, tangential, and axial directions, respectively. ψ₁, ψ₂ and ψ₃ are unknown displacement functions in the r, θ, and z directions, respectively.

Considering the cylindrical symmetry of the circular plate about the coordinate θ, the displacement amplitude functions can be written as:

 

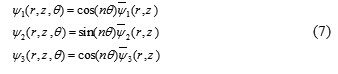
Where the non-negative integer n represents the circumferential wave number of the corresponding mode shape. It is obvious that n=0 leads to an axisymmetric vibration. Rotating the symmetry axes by π/2, another set of free vibration modes can be obtained, corresponding with an interchange between cos (nθ) and sin (nθ) in Eq. (7); however, in such a case, n=0 represents a torsional vibration.  is the displacement function in the r and z coordinates.

To simplify the equations, the following dimensionless parameters are introduced:

 

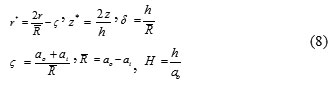
Using the displacement field given in equation (6), the strain components ε_ij (i,j=r,θ,z) for small deformations are defined as follows:

 

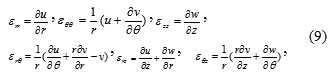
The strain (potential) energy V of a three-dimensional elastic circular plate undergoing free vibration in circumferential coordinates is expressed in terms of the strains (ε_ij) and the stress (σ_ij) as:

 

And the kinetic energy for free vibration is:

 

The Lagrangian energy functional (Π) of the plate is defined as:

 

The displacement amplitude functions may be assumed in the form of a double series of Chebyshev polynomials multiplied by boundary functions as follows:

 

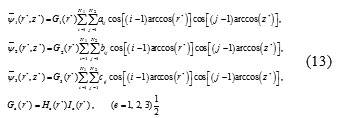
In which a_ij, b_ij and c_ij are the undetermined coefficients; i and j are integers; N₁ and N₂ are the highest degrees taken in the polynomial terms, and   G_e (r^*); (e=1, 2, 3) are functions depending upon the geometric boundary conditions to be enforced. It should be emphasized that in the Chebyshev–Ritz method, the displacement functions u, v and w should satisfy the geometric boundary conditions of the plate. The boundary function components in outer edge       I_e (r^*) and inner edge H_e (r^*); (e=1, 2, 3) of annular plate corresponding to different combinations of boundary conditions.

To obtain natural frequencies, the eigenvalue problem is formulated by minimizing the Lagrangian energy functional with respect to the arbitrary coefficients a_ij, b_ij and c_ij Thus we have:

 

which in turn leads to the following eigenfrequency equation in matrix form as:

 

and

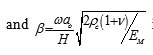
is the frequency parameter. Parameter H is plate thickness.

Solving the eigenvalue Eqs. (14)- (16) yield the frequency parameters β.

Numerical results and discussion

The properties of the carbon nanotubes and matrix which were used in this article are presented in Figs. 2 and Table 1.

Table 1: Mechanical properties of the carbon nanotubes and matrix [31]

Mechanical properties	SWNTs	MWNTs	Matrix (LY-5052)
Diameter (nm)	10	25	–
(GPa)	1200	1000	3.11
(GPa)	6.63	15.58	3.11
(GPa)	442	320	1.2
(GPa)	17	4.1	1.2
	0..20	0.25	0.35
(kg/m3)	1350	1250	1100

 

According to Fig. 2(a), a strong linear relationship between the nanotube diameter and wall thickness can be observed [39]. From the measurement of inside and outside diameter, the nanotube density per unit length can be calculated by assuming that the graphite layers of the tube shell have the density of fully dense graphite (ρ_g = 2.25 g/cm³). The nanotube density as a function of diameter is shown in Fig. 2(b), where the curved line is obtained directly from the straight line in Fig. 2(a). The morphology of a carbon nanotube is determined by the orientation and magnitude of the chiral vector in a graphene sheet, which is wrapped up to form the single-walled carbon nanotube (SWCNT). The two configurations are armchair and zigzag nanotubes. The Young’s modulus as function of nanotube diameter, obtained by using molecular structural mechanics (Li and Chou [34]), tight-binding molecular dynamics (Hernandez et al. [35]), and experimental data (Krishnan et al. [37]) are presented in Fig. 2(c). For molecular structural mechanics, the results are sensitive to nanotube diameter and nanotube structure at small diameter. The axial Young’s modulus approaches to 1.03 TPa for diameters 1.0 nm.

Numerical solutions for the 3-D vibration analysis of nanocomposites annular plates for various geometry and boundary condition were computed. The vibration frequency β was expressed in terms of a non-dimensional frequency parameter.

 

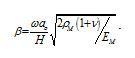
In order to check the stability of the proposed approach as well as to validate the accuracy of that, some convergence tests and comparison studies were performed.

For the convergence study, the first four frequency parameters (e.g. nanocomposite annular plate) of completely free nanocomposites annular plate with inner-outer radius ratio a_i/a _o= 0.6 different thickness-radius ratio H, κ_o = 0.2, κ_w = 0.4, E_NT/M = 321.5, C = 2000, α = -11.83, ρ_NT/M = 1 and MWCNT volume fraction V_NT = 0.5% and 4% were performed, with results listed in Table 2. Four groups of series terms were taken into account, as shown in Table 2, where N₁ means the number of terms used in the radial direction and N₂ means those used in the thickness direction for each displacement component. From the frequency parameters presented in Table 2, it can be observed that when the used terms were set to be N₁= 10 and N₁= 10 to five significant figures.

Figure 2: Variation in: (a) nanotube wall thickness with nanotube diameter and (b) density with nanotube diameter [39]. (c) Diameter sensitivity of elastic modulus predicted by molecular structural mechanics (Li and Chou [34]), tight-binding molecular dynamics (Hernandez et al. [35]) and experimental data (Krishnan et al. [37]).  Click here to View figure

 

The three-dimensional free vibrations of a thick annular plate with different boundary conditions, thickness ratio, and inner-outer radius ratio, V_NT = 0 and υ_m = 0.3 are presented in Table 3 together with the published values of  Liew and Yang [15] and Hosseini Hashemi et al. [17]. From Table 3, it is found that the present results were in close agreement with both Liew and Yang [15] and Hosseini Hashemi et al. [17].

Table 2: Convergence of the first six frequency parameters of completely free nanocomposites annular plate when κ_o = 0.2, κ_w = 0.4, E_NT/M = 321.5, C = 2000, α = -11.83, a_i/a _o= 0.6, ρ_NT/M = 1

H	VNT	N1×N2	Mode sequence number
			1	2	3	4
0.1	0.5	7×7	2.4101	6.7018	6.8045	7.8216
		10×10	2.4100	6.7017	6.8045	7.8216
		14×14	2.4100	6.7017	6.8045	7.8216
		21×21	2.4100	6.7017	6.8045	7.8216
	4	7×7	3.0467	8.4727	8.6018	9.8878
		10×10	3.0466	8.4726	8.6018	9.8878
		14×14	3.0466	8.4726	8.6018	9.8878
		21×21	3.0466	8.4726	8.6018	9.8878
0.4	0.5	7×7	1.6944	1.9580	3.9905	4.2921
		10×10	1.6944	1.9580	3.9905	4.2921
		14×14	1.6944	1.9580	3.9905	4.2921
		21×21	1.6944	1.9580	3.9905	4.2921
	4	7×7	2.1420	2.4754	5.0460	5.4258
		10×10	2.1420	2.4754	5.0460	5.4258
		14×14	2.1420	2.4754	5.0460	5.4258
		21×21	2.1420	2.4754	5.0460	5.4258

 

Figure 3(a) shows comparison of the experimental data and theoretical prediction models for the Young’s modulus of MWCNT/epoxy composites as a function of CNT content [31]. The previous micromechanical models (Micro-Mechanical Mori-Tanaka, Halpin-Tsai method, and rule of mixtures) reported in the literature failed with the increase of the wt% of MWCNTs. Since the frequency parameter is completely depend on the Young’s modulus, the previous micromechanical models (Micro-Mechanical Mori-Tanaka, Halpin-Tsai method, and rule of mixtures) cannot calculate the frequency parameter correctly.

Table 3: Comparison of the first six frequency parameters resulted from the presented study by Liew and Yang [15] and Hosseini Hashemi et al. [17] when V_NT = 0 and υ = 0.3

H	ai/a o	Source of results	Mode sequence number
			1	2	3
An annular plate with both outer and inner edges free (F-F)
0.20	0.3	Ref a	2.2079	3.7727	5.3255
		Authors	2.2079	3.7727	5.3255
0.35	0.1	Ref b	2.2901	3.7086	4.8676
		Authors	2.2901	3.7086	4.8676
An annular plate with simply supported outer edge and free inner edge (S-F)
0.20	0.3	Ref a	2.1698	5.3719	6.0898
		Authors	2.1698	5.3719	6.0898
0.35	0.1	Ref b	2.1789	3.3439	5.3938
		Authors	2.1789	3.3439	5.3938
An annular plate with clamped outer edge and free inner edge (C-F)
0.20	0.3	Ref a	4.9934	7.6593	12.258
		Authors	4.9934	7.6593	12.258

^aLiew and Yang [15]

^bHosseini Hashemi et al. [17

Figure 3: (a) Comparison of the experimental data and theoretical predicting models for the Young’s modulus of CNT/epoxy composites [31]. The first frequency parameter of the annular plate with free outer edge and clamped inner edge (F-C) versus CNT volume fraction (VNT) by using the different theory when H =0.3, ai/a o= 0.5, κo = 0.2, C = 2000 (b) MWNT κw = 0.6, ENT/M = 321.5, ρNT/M = 1.9. (c) SWNT κw = 0.6, ENT/M = 354.43, ρNT/M = 1.1    Click here to View figure

 

To validate the other well-known theories (rule of mixtures, Micro-Mechanical and Halpin Tsai) results with respect to the change of the CNT volume fraction (V_NT),   the curves of the frequency parameter β versus V_NT are shown in Figs. 3 (b) and (c) for the modified rule of mixtures and the three other theories for a thick annular plate ((a_i/a _o)→ 0.5)  with free outer edge and clamped inner edge (F-C) boundary conditions, thickness ratio H = 0.3,  and C = 2000. As shown in Fig. 3, when CNT volume fraction (V_NT) takes the values larger than 1%, as less the other theories give incorrect results. This is due to the fact that the variation of mechanical properties of CNT/polymer composites against CNT loading is nonlinear, whereas in these well-known theories the relationship between mechanical properties of CNT/polymer composites and CNT loading is assumed to be almost linear. This assumption is acceptable within the low wt% of CNTs (e.g. in ref. [31] wt% ≤ 1.5%).

The effect of CNT type, structures, diameter, shape factor and density on the vibration behavior of the annular plates are shown in Figs. 4-7, in which the variation of the frequency parameters plotted against the CNT volume fraction (V_NT) where ((a_i/a _o)→ 0.5)  and .

The first frequency parameter of the completely free annular plate versus CNT volume fraction (V_NT) for the zigzag and armchair structures of both MWNTs and SWNTs is shown in Fig. 4. It can be seen that CNT structural form (zigzag or armchair) of SWNT has a stronger effect on frequency parameter than MWNTs.

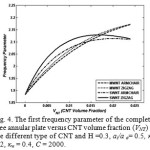Figure 4: The first frequency parameter of the completely free annular plate versus CNT volume fraction (VNT) for the different type of CNT and H =0.3, ai/a o= 0.5, κo = 0.2, κw = 0.4, C = 2000.  Click here to View figure

 

Figure 5 depicts the effect of CNT diameter on the first frequency parameter of the completely free annular plate. In Fig. 5(a) the MWNT diameter value was varied from 10 nm to 50 nm, while for Fig. 5(b) the SWNT diameter value was varied from 0.8nm to 1.1nm. As can be clearly seen, increasing of either MWNT and SWNT values had a decreasing effect on the first frequency parameter, but, in comparison, the MWNT had a stronger influence on the frequency changes that for the SWNT which were nearly increasing diameters of independent of diameter changes.

Figure 5: The first frequency parameter of the completely free composite plate versus CNT volume fraction (VNT) for the different value of CNT diameter when H =0.3, κo = 0.2, C = 2000, ai/a o= 0.5. (a) MWNT κw = 0.4, ENT/M = 321.5, α = -11.83 (b) SWNT κw = 0.6, ENT/M = 354.43, α = -7.63 [31]  Click here to View figure

 

The influence of the CNT shape factor parameter (c) on the first frequency parameters of the completely free annular plate for the different values of c from 200 to 20,000 is shown in Fig. 6. An increase in parameter c had resulted in an increase of the frequency parameter, especially in the middle of the domain where V_NT was 5% for both the MWNT and SWNT cases.

Figures 7 a and b show the first frequency parameter of the completely free annular plate versus CNT volume fraction (V_NT) for ρ_NT/M changes from 0.25 to 2 for the two cases, MWNT and SWNT, respectively. As they show, an increse in parameter ρ_NT/M  had a decreasing effect on the frequency parameter for both MWNT and SWNT cases, but the MWNT samples were more affected by ρ_NT/M changes, increasing up to 20, than SWNT where it grew up to 16 for a maximum of ρ_NT/M equaled to 2, especially at the middle of the figures where V_NT  equals 5% for both MWNT and SWNT cases.

Figure 6: The first frequency parameter of the completely free annular plate versus CNT volume fraction (VNT) for the different value of CNT shape factor when. H =0.3, κo = 0.2, κw = 0.6, ai/a o= 0.5. (a) MWNT ENT/M = 321.5, (b) SWNT ENT/M = 354.43 [31] Click here to View figure

 

Figure 7: The first frequency parameters of the annular plate with free outer edge and clamped inner edge (F-C) versus CNT volume fraction (VNT) for the different value of   when H =0.3, κo = 0.2, κw = 0.6, ai/a o= 0.5. (a) MWNT ENT/M = 321.5, (b) SWNT ENT/M = 354.43. Click here to View figure

 

Conclusions

Based on the 3-D elasticity theory, a comprehensive study of the three-dimensional vibration analysis of carbon nanotube (CNT) reinforced composites annular plates with different combinations of free, simply-supported, and clamped boundary conditions at the inner and outer edges was investigated. The Chebyshev–Ritz method was applied to derive the eigenvalue. Due to the cylindrical nature of the annular plate geometry, the formulation was carried out in cylindrical polar coordinates.

In order to obtain precise results, a new form of the rule of mixtures, including an exponential shape function, length efficiency parameter κ_l, orientation efficiency factor κ_o, and waviness parameter κ_w was applied to have a proper prediction of the mechanical properties of CNT reinforced composites [31].

The validity and the range of applicability of the results was obtained based on other well-known theories (e.g., Halpin-Tsai, etc.) were studied by comparing results obtained using them with those obtained by our modified rule of mixtures. Moreover, the influence of the CNT type, structures, diameter, shape factor, density and volume fraction on the frequency parameter of the plate was also studied.  Finally, we suggest the results presented in this paper can serve as benchmark results for researchers to validate their numerical methods and also for engineers to use such plates in their structures in the future.

Reference

1. Allaoui, A.; Bai, S.; Cheng, H.M.; Bai, J.B. Compos. Sci. Technol. 2002, 62, 1993-1998
   CrossRef
2. Azizian, J.; Hekmati, M.; Dadras, O. G. Orient. J. Chem. 2014, 30(2), 667-673
   CrossRef
3. Baniasadi, L.; Omidi, M.; Amoabediny, G.; Yazdian, F.; Attar, H.; Heydarzadeh, A.; Zarami, A.S.H.; Sheikhha, M.H. Enzyme Microb. Technol. 2014, 63, 7-12
   CrossRef
4. Ardjmand, M.; Omidi, M.; Choolaei, M. Orient J Chem., 2015, 31(4), 2291-2301
5. Omidi, M.; Malakoutian, M.A.; Choolaei, M.; Oroojalian, F.; Haghiralsadat, F.; Yazdian, F. Chin. Phys. Lett. 2013, 30(6), 068701.
   CrossRef
6. Omidi, M.; Amoabediny, G.; Yazdian, F.; Habibi-Rezaei, M. Chin. Phys. Lett. 2015, 32(1), 018701.
   CrossRef
7. Soleymani, R.; Torkashvand, F.; Farsi-Madan, S.; Bayat, M. Orient J Chem., 2012, 28(2), 733-740
8. Rokni, H.; Milani, A.S.; Seethaler, R.J.; Omidi, M. Int. J. Compos. Mater. 2013, 3(A), 45-57.
9. Andrews R, Weisenberger MC. Curr Opin Solid St Mat Sci 2004, 8, 31
   CrossRef
10. Ci L, Bai JB. Compos Sci Technol 2006, 66, 599
    CrossRef
11. Yeh MK, Hsieh TH, Tai NH. Sci Eng A 2008, 483, 289
    CrossRef
12. J. So, A.W. Leissa, J Sound Vibrat 1998, 209, 15
    CrossRef
13. K.M. Liew, B. Yang, Int J Solids Struct 2000, 37, 7689
    CrossRef
14. Taher, H.R.D.; Omidi, M.; Zadpoor, A.A.; Nikooyan, A.A.  J. Sound. Vib. 2006, 296(4), 1084-1092
    CrossRef
15. K.M. Liew, B. Yang, Int J Solids Struct 2000, 37, 7689
    CrossRef
16. D. Zhou, F.T.K. Au, Y.K. Cheung, S.H. Lo, Int J Solids Struct 2003, 40, 3089
    CrossRef
17. Hashemi, S.H.; Taher, H.R.D.; Omidi, M. J. Sound. Vib.  2008, 311(3), 1114-1140
    CrossRef
18. Hashemi, S.H.; Omidi, M.; Taher, H.R.D. Eur. J. Mech. A Solids 2009, 28(2), 289-304
    CrossRef
19. W. Lessia, NASA SP 160, Vibration of Plates, 1969
20. Omidi, M.; Alaie, S.; Rousta, A. Meccanica 2012, 47, 817-833
    CrossRef
21. Hedayati, H., and B. Sobhani Aragh. Appl Math Comput 2012, 218, 8715
    CrossRef
22. Zhu, Ping, Z. X. Lei, and K. M. Liew. Compos Struct 2012, 94, 1450
    CrossRef
23. Pouresmaeeli, S., E. Ghavanloo, and S. A. Fazelzadeh. Compos Struct 2013, 96, 405
    CrossRef
24. Valavala PK, Odegard GM. Rev Adv Mat Sci 2005, 9, 34
25. Odegard GM, Gates TS, Wise KE, Park C, Siochi EJ. Compos Sci Tech 2003, 63, 1671
    CrossRef
26. Seidal GD, Lagoudas DC. Mech Mat 2006, 38, 884
    CrossRef
27. Anumandla V, Gibson RF. Compos part A 2006, 37, 2178
    CrossRef
28. Shao LH, Luo RY, Bai SL, Wang J. Compos Struct 2009, 87, 274
    CrossRef
29. Kanagaraj S, Varanda RF, Zhil’tsova VT, Oliveira ASM, Simoes OAJ. Compos Sci Technol 2007, 67, 3071
    CrossRef
30. Bokobza L. Polym 2007, 45, 4907
    CrossRef
31. Omidi, M.; DT, H.R.; Milani, A.S.; Seethaler, R.J.; Arasteh, R. Carbon 2010, 48(11), 3218-3228
    CrossRef
32. Mori T., Tanaka K. Acta Metal 1973, 21, 571
    CrossRef
33. Cox HL. Br J Appl Phys 1952, 3, 72
    CrossRef
34. Li CY, Chou TW. Int J Solids Struct 2003, 40, 2487
    CrossRef
35. Hernandez E, Goze C, Bernier P, Rubio A. Phys Rev Lett 1998, 80, 4502
    CrossRef
36. Lu JP. Phys Rev Lett 1997, 79, 1297
    CrossRef
37. Krishnan A, Dujardin E, Ebbesen TW, Yianilos PN, Treacy MMJ. Phys Rev B 1998, 58, 14013
    CrossRef
38. Erik T. Thostenson, Chunyu Li, Tsu-Wei Chou. Compos Sci Tech 2005, 654, 91
39. Thostenson ET, Chou TW. J Phys D: Appl Phys 2003, 36, 573
    CrossRef
40. Yeh MK, Tai NH, Liu JH. Carbon 2006, 44, 1
    CrossRef

---

This work is licensed under a Creative Commons Attribution 4.0 International License.