Density of state (DOS) for Zig-Zag, Chiral and Armchair SWCNTs and DWBNNTs: In viewpoint of Electronics and Structure

Introduction

Control and designing of nanotube diameter is needed for developing nanotube growth methods. Nanotubes with a diameter of less than 10 angstrom provide the ideal nano space in one-dimension. Twenty years ago, it was been suggested that the size of the growth catalyst used in metal^[1] catalyzed chemical vapor deposition (CVD) can define the diameter of as-grown carbon nanotubes ^[2]. This idea has been confirmed by the observation that catalytic particles at the ends of CVD-grown nanotubes have sizes proportionate with the nanotubes diameters ^[3].

Small-diameter carbon nanotubes exhibit many exotic properties such as anisotropic optical absorption spectra ^[4] and superconductivity originated from a Peierls distortion ^[5].

These findings have stimulated much interest in study of small nanotubes both experimentally and theoretically

Boron nitride nanotube (BNNT), which firstly predicted and synthesized by Rubio and Chopra respectively ^[6], has a structural analogy to CNT but, contrary to the CNT being metallic (semiconductor) depending on chirality. BNNTs are usually can be an insulator regardless of their helicity, tube diameters and number of tube walls ^[7].

Besides, the study on double-walled BNNTs (DBNNTs) has demonstrated an interesting variation in their electronic properties when compared with those of freestanding component of BNNTs ^[8]. So it is also important to see the inter-wall coupling behavior and interaction energies associated with the small BNNTs.

Boron nitride nanotubes possess a large band gap [ 6) eV)] irrespective of the number of walls, diameters, electronic properties and chirality ^[9] In addition, they are so stable in viewpoint of chemical and mechanical structures ^[10]. Therefore, thin single-wall BNNTs (SWBNNs) can widely be used as an ideal nanotube for nano science to produce special materials such as atomic wires, capacitors and semiconductors. In our study the SWBNNs is a suitable material as an insulator to produce nano-cylindrical capacitors.

They used arc-grown SWCNTs (with a diameter distribution of 1.4  0.1 nm) as a template to synthesize thin SWBNNTs. The uniform diameter distribution of SWCNT-templates is essential to realize a diameter selective synthesis of BNNTs (diameter of 0.7  0.1 nm has expected for thin SWBNNTs by them)

In this work we have calculated our systems based on the various distribution diameters of SWBNNTs and SWCNTs .The effects of these doping on the electrostatic properties of the inner and outer tubes can also be calculated for any further comparison and discussion.

Monajjemi and coworkers have simulated a large range of the nanotube carbons and other molecules via a wide range of methods and basis sets [11-127]

Zigzag BNNTs (n, 0) are expected to have direct band gap. On the other hand, armchair BNNTs (m, m) will have indirect band gap [128]. Because of their large band gap of (~5 eV), experiments using BNNTs as the conduction channel for field-effect transistors (FETs) showed that BNNTs allowed transport through only the valence band.

Another important feature about the band gaps of BNNTs is that they are tunable by doping with carbon , radial deformation ,or by applying a transverse electric field across the BNNT “so-called giant stark effect” [129].

Theoretical band structure calculations suggested that SWBNNT can either be p-type or n-type semiconductors by controlling the composition of carbon into SWBNNTs. Carbon impurities on the boron sites result in electron carriers while on the nitrogen sites result in hole carriers [130].

On the other hand, the band-gap modification by radial deformation in BNNTs was predicted through first-principles pseudo-potential density-functional calculations.

In zigzag BN nanotubes, radial deformations due to transverse pressures of about 10 GPa decrease the direct band gap of BNNTs from 5 to 2 eV, allowing for optical applications in the visible range [130].However, the band gaps of armchair BNNTs are found to be insensitive to radial deformations. Finally, theory indicates that the band gap of BNNTs can be reduced and even completely removed by the application of transverse electric field onto BNNTs and simultaneously probing the electronic properties.

In this study we exhibited that the piezoelectricity for BNNTs causes to increase the capacity of BNNTs @ X doped-CNTs capacitor compare to CNTs @ CNTs. This phenomenon theoretically originated from the deformation effect due to the rolling of the planar hexagonal BN networks to form tubular structures [131]. Nakhmanson and coworkers showed that BNNT could be excellent piezoelectric systems [132]. As an example of calculations, piezoelectric constant for different zigzag BNNTs was found to increase along with the decrease of the radius of BNNTs [132] Experimentally, Bai et al. have shown that under in situ elastic bending deformation at room temperature inside a 300-kV high-resolution transmission electron microscope, a normally electrically insulating MW-BNNT may transform to a semiconductor [133].

One of the main purposes in this study of explaining the capacitor model is concerning the interaction between SWCNTs and SWBNTs is both of electronic transport properties and energy analysis. Although there are many data and a novel method for electronic transport reports for the double-wall carbon nanotubes, for BNNTs @ WCNTs there are not significant works, spatially the subject of this work for BNNTs @ X-doped-WCNTs is completely new.

Based on previous works, we simulated our model in viewpoint of various diameters and chirality by considering the SWCNTs and SWBNNTs.

The electronic structure

The electron density has been defined as p(r) = ηi |Φi(r)|²= |Σ_iη_i |Σ_iC_∫,iXi(r)|²    (1) [134-136] Where  ηi is occupation number of orbital(i) Φ is orbital wave functionχ, c is basis function and C is
coefficient matrix, the element of i_th row j_th column corresponds to the expansion coefficient of orbital j respect to basis function i. Atomic unit for electron density can be explicitly written as e/Bohr³. 

The kinetic energy density is not uniquely defined, since the expected value of kinetic energy operator

formula5<Φ|-(1/2)>Relative to K(r), the local kinetic energy definition given below guarantee positivizes everywhere; hence the physical meaning is clearer and is more commonly used. The Lagrangian kinetic energy density, “G(r)” is also known as positive definite kinetic energy density.

K(r) and G(r) are directly related by Laplacian of electron density

Becke and Edgecombe noted that spherically averaged likespin conditional pair probability has direct correlation with the Fermi hole and then suggested electron localization function (ELF) [135]. ELF(r)

 

Savin et al. have reinterpreted ELF in the view of kinetic energy, which makes ELF also meaningful for Kohn-Sham DFT wave-function or even post-HF wave-function. They indicated that D(r) reveals the excess kinetic energy density caused by Pauli repulsion, while D0(r) can be considered as Thomas-Fermi kinetic energy density. Localized orbital locator (LOL) is another function for locating high localization regions likewise ELF, defined by Schmider and Becke in the paper. We have calculated the Hamiltonian kinetic energy and density Electron localization function of lithium in diffusion model for several of SWBNNTs, SWCNTs and WBNNTs @ SWCNTs

The Total electrostatic potential (ESP) measures the electrostatic interaction between a unit point charges placed at r and the system of interest. A positive (negative) value implies that current position is dominated by nuclear (electronic) charges. Molecular electrostatic potential (ESP) has been widely used for prediction of nucleophilic and electrophilic sites for a long time.

It is also valuable in studying hydrogen bonds, halogen bonds, molecular recognitions and the intermolecular interaction of aromatics. The ESP evaluated under default value is accurate enough in general cases.

Computational details

Calculations were performed using Gaussian 09 and GAMESS-US packages [137]. In this study, we have mainly focused on getting the optimized results for each tube from HF and DFT methods including the B3lyp and Blyp. Extendedhuckel calculations using Gaussian program have done for the non-bonded interaction between BNNTs and X-doped-SWNTs which are monotonous through the comparison between different situations.

Geometry optimizations and electronic structure calculations for tubes have been carried out using the 6-31g and 6-31g* basis sets.

A  fixed BNNT geometry with B-N bond  lengths of 1.445 Å, and B-H and N-H bond lengths  of  1.185  Å  and  1.05  Å,  respectively,  are  chosen  with  no  further  geometry optimization. The outer ring,  initially placed at  the center of  the  inner  tube,  is  rigidly axially  shifted  and  rotated  around  the  fixed  inner  shell.

The charge transfer and electrostatic potential-derived charge were also calculated using the Merz-Kollman-Singh [138], chelp [139] or chelpG [140] the charge calculation methods based on molecular electrostatic potential (MESP) fitting are not well-suited for treating larger systems whereas some of the innermost atoms are located far away from the points at which the MESP is computed.

In such a condition, variations of the innermost atomic charges will not lead towards a significant change of the MESP outside of the molecule, meaning that the accurate values for the innermost atomic charges are not well-determined by MESP outside the molecule. This approach (CHELPG) is shown to be considerably less dependent upon molecular orientation than the original CHELP program. The results are compared to those obtained by using CHELP.

In the CHELPG (Charges from Electrostatic Potentials using a Grid based method), atomic charges are fitted to reproduce the molecular electrostatic potential (MESP at a number of points around the molecule. The MESP is calculated at a number of grid points spaced 3.0 pm apart and distributed regularly in a cube. Charges derived in this way don’t necessarily reproduce the dipole moment of the molecule. CHELPG charges are frequently considered superior to Mulliken charges as they depend much less on the underlying theoretical method used to compute the wave function (and thus the MESP)[141-142].

Result and Discussion

The results are shown in Figs 1-7 and tables1. The system has been modeled with Armchair, Zigzag and Chiral as an impurity among the atoms of the outer nanotube layer. The total energy contains three terms including the band structure energy of the inner and outer tubes and the electrostatic energy of the layers charge distribution. In this model, the SWBNNTs compare to SWCNTs tubes have been chosen by various diameters, therefore, as the SWNTCs, the boron atom also undergoes the sp² hybridization. Due to the relatively similar size of C and B, no significant distortion in 3-D structure of tube is expected, except for the change in adjoining the bond length. By doping the boron atoms in SWNTCs, the Fermi level shifts significantly below the Dirac point resulting in a p-type doping. This would break the symmetry of tubes into two sub layers due to presence of the B atoms which would eventually lead towards a change of the behavior of tubes from semimetal to conductor.

It is shown that the buckling rapidly increases with decreasing the tube diameter but is nearly independent of the chirality. This result is consistent with the reported trend revealed by tight-binding and ab initio calculations. The wall buckling is driven by different hybridizations related with the B and N atoms.

Two physical effects act in concert to segregate most of the holes onto the outer nanotube. First, the band gaps of the smaller diameter tubes tend to be larger, so they empty last. Second, the cylindrical geometry preferentially raises the electrostatic potential at the inner tube. Only the charge on the inner tube affects the potential difference between the two layers. Figures 1 shows the results of the energy minimization. The stability of small BNNTs encapsulated in a larger x-doped CNT is confirmed by this work. As the total energies of the small BNNTs are higher than those of their uncurled states, examination the behavior of the small BNNTs inside a larger BNNT should be necessary. It is apparent that the small BNNTs become globally stable in their energy favorable outer shells. Encapsulation induced enhancement in stability should be able to extend into other small BNNTs. The electronic properties of SWCNTs and SWBNNTs are listed in table1.

We will call the lowest π*  state as singly degenerate state hereafter for all the small BNNTs. In BNNTs, the π* states are mainly distributed on the B atoms from the pz orbitals perpendicularly to the tube wall. So it can be imagined that a shorter B-B distance along the circumference will be more favorable for an overlapping of the singly degenerate state inside the tube, thus enhancing the π* -σ* hybridization. With increasing chiral angle of the BNNT, there are two primary variations that could significantly affect such overlapping: (i) Increasing nearest B-B distance along the circumference.

Besides, we also note that the repulsion between the NFE and π* bands becomes increasingly significant from the (2, 2) to (4, 0) BNNTs, indicating that the NFE-π* hybridization becomes stronger with decreasing chiral angle as well. This phenomenon gives us a hint that the amplitude of NFE-π hybridization is proportional to that of π*σ* hybridization. On the other hand, it is found that the nearest B-B distance along the circumference can also be reduced by decreasing the tube diameter, which is decreased to 2.16 Å in the (3, 0) BNNT. That is why the energy gap displays apparent diameter dependence in the small zigzag BNNTs.

The data of Density of all electron, Density of electron, Density of electron, Potential energy density, Hamiltonian,  kinetic energy, Hamiltonian  kinetic Energy, LOL, local Entropy, ellipticity, ELF, eta index of several atoms in nanotube have listed in table1. For calculation the electron spin density from the difference between alpha and beta density, we have used p^s(r) = pα(r)- p^β(r) then the spin polarization parameter function will be returned instead of spin density ξ(r)=p^α(r)-p^β(r)/pα(r)+p^β(r). The kinetic energy density, Lagrangian kinetic energy density, and the electrostatic potential from nuclear / atomic charges can be calculated as the 1-5 eqs. 

The larger the electron localization is in a region, the more likely the electron motion is confined within it. If electrons are completely localized, then they can be distinguished from the ones outside. Bader found that the regions which have large electron localization must have large magnitudes of Fermi hole integration. However, the Fermi hole is a six-dimension function and  thus difficult to be studied visually.

Since D0(r) from eqs. 5-10 is introduced into ELF as reference, what the ELF reveals is actually a relative localization. ELF is within the range of [0, 1]. A large ELF value means that electrons are greatly localized, indicating that there is a covalent bond, a lone pair or inner shells of the atom involved. ELF has been widely used for a wide variety of systems, such as organic and inorganic small molecules, atomic crystals, coordination compounds, clusters, and for different problems, such as the revealing atomic shell structure, classification of chemical bonding, verification of charge-shift bond, studying aromaticity.

LOL has similar expression compared to ELF. Actually, the chemically significant regions that highlighted by LOL and ELF are generally qualitative comparable, while Jacobsen pointed out that LOL conveys more decisive and clearer picture than ELF, Obviously LOL can be interpreted in kinetic energy way as for ELF; however LOL can also be interpreted in view of localized orbital. Small (large) LOL value usually appears in boundary (inner) region of localized orbitals because the gradient of orbital wave-function is large (small) in this area. The value range of LOL is identical to ELF, namely [0, 1].

Figure 1: Various SWCNTs and SWBNNTs inside together to produce DWBNNTs &DWCNTs  Click here to View figure

 

Figure 2: Density of state for SW (4, 4) BNNTs@ (10, 10) SWBNNTs  Click here to View figure

 

Figure 3: Counter map of (5,5)SWBNNTs  Click here to View figure

 

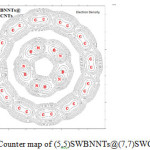Figure 4: Counter map of (5,5)SWBNNTs@(7,7)SWCNNTs  Click here to View figure

 

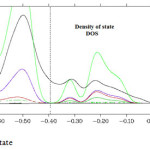Figure 5: Density of state  Click here to View figure

 

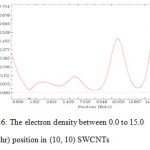Figure 6: The electron density between 0.0 to 15.0 (Bohr) position in (10, 10) SWCNTs  Click here to View figure

 

Table 1: Density, energy, Electron localization function (ELF), Localized orbital locator (LOL) and Local Entropy for C, B and N in various SWBNNTs and SWCNTs&nbsp

Atom

No.Density of all electron

 (10^-4)Density of electron

 (10^-4)Density of electron

 (10^-4)Potential energy density

( 10^-3J)Hamiltonian  kinetic

Energy

( 10^-4J)LOL

 

 

10^-3Local

Entropy

 

10^-6EllipticityELF

 

 

10^-7Eta

indexC(10)0.280.140.14-0.20-0.100.150.50-0.450.410.15B(20)0.200.100.10-0.22-0.140.130.59-0.330.400.13N(21)0.240.120.12-0.26-0.120.230.51-0.330.420.14C(4)0.260.130.13-0.22-0.140.210.55-0.260.410.15B(6)0.320.160.16-0.28-0.150.260.47-0.490.350.11N(7)0.360.180.18-0.24-0.170.210.41-0.190.310.12

References

1. M. Topsakal, S. Ciraci, Phys. Rev. B 85, 045121. (18-20) (2012)
2. Dai, H. J.; Rinzler, A. G.; Nikolaev, P.; Thess, A.; Colbert, D. T.; Smalley, R. E. Chem. Phys. Lett. 260, 471, (1996)
3. Sinnott, S. B.; Andrews, R.; Qian, D.; Rao, A. M.; Mao, Z.; Dickey, E. C.; Derbyshire, F. Chem. Phys. Lett. 315, 25, (1999)
4. Chin Li Cheung, Andrea Kurtz, Hongkun Park, and Charles M. Lieber, Diameter-Controlled Synthesis of Carbon Nanotubes , J. Phys. Chem. B, 106, 2429 2433, (2002)
5. Z. M. Li, Z. K. Tang, H. J. Liu, N. Wang, C. T. Chan, R. Saito, S. Okada, G. D. Li J. S. Chen, N. Nagasawa, and S. Tsuda, Phys. Rev. Lett. 87, 127401 (2001)
6. A. Rubio, J. L. Corkill, and M. L. Cohen, Phys. Rev. B 49, 5801 (1994).
7. S. Okada, S. Saito, and A. Oshiyama, Phys. Rev. B 65, 165410 (2002).
8. Xiang, H., Yang, J., Hou, J. & Zhu, Q. Phys. Rev. B 68, 035427 (2003).
9. Chen, Y., Zou, J., Campbell, S. J. & Le Caer, G. Appl. Phys. Lett. 84, 2430–2432, (2004)
10. Kitaura, R. et al. Angew. Chem. Int. Ed. 48, 8298–8302, (2009)
11. Monajjemi, M.; Lee, V.S.; Khaleghian, M.; B. Honarparvar, B.; F. Mollaamin, F. J. Phys.Chem C. 2010, 114, 15315
12. Monajjemi, M. Struct Chem. 2012, 23,551–580
13. Monajjemi, M.; Chegini, H.; Mollaamin, F.; Farahani, P.  Fullerenes, Nanotubes, and Carbon Nanostructures. 2011, 19, 469–482
14. Monajjemi, M .; Afsharnezhad ,S.; Jaafari , M.R.; Abdolahi ,T.; Nikosade ,A.; Monajemi ,H.; Russian Journal of physical chemistry A, 2007, 2,1956-1963
15. Monajjemi, M.; Baei, M.T.; Mollaamin, F. Russian Journal of Inorganic Chemistry. 2008, 53 (9), 1430-1437
16. Monajjemi, M.; Rajaeian, E.; Mollaamin, F.; Naderi, F.; Saki, S. Physics and Chemistry of Liquids. 2008, 46 (3), 299-306
17. Monajjemi, M.;  Boggs, J.E.  J. Phys. Chem. A, 2013, 117, 1670 −1684
18. Mollaamin, F.; Monajjemi, M, Journal of Computational and Theoretical Nanoscience. 2012, 9 (4) 597-601
19. Monajjemi, M.; Khaleghian, M, Journal of Cluster Science. 2011, 22 (4), 673-692
20. Mollaamin, F.; Varmaghani, Z.; Monajjemi, M, Physics and Chemistry of Liquids. 2011, 49 318
21. Nafisi, S.; Monajemi, M.; Ebrahimi, S. Journal of  Molecular Structure. 2004,705 (3) 35-39
22. Fazaeli, R.; Monajjemi, M.; Ataherian, F.; Zare, K. Journal of Molecular Structure: THEOCHEM.2002, 581 (1), 51-58
23. Monajjemi, M.;  Razavian, M.H.;  Mollaamin,F.;  Naderi,F.;  Honarparvar,B.; Russian Journal of Physical Chemistry A , 2008 , 82 (13),  2277-2285
24. Monajjemi, M.; Seyed Hosseini, M.; Mollaamin, F. Fullerenes, Nanotubes, and Carbon Nanostructures. 2013, 21, 381–393
25. Monajjemi, M.; Faham, R.; Mollaamin, F. Fullerenes, Nanotubes, and Carbon Nanostructures, 2012 20, 163–169
26. Mollaamin, F.; Najafi, F.; Khaleghian, M.; Khalili Hadad, B.; Monajjemi, M.  Fullerenes, Nanotubes, and Carbon Nanostructures, 2011 19, 653–667
27. Mollaamin, F.;  Baei, MT.;  Monajjemi, M.; Zhiani, R.;  Honarparvar, B.;
28. Russian Journal of Physical Chemistry A, Focus on Chemistry, 2008, 82 (13), 2354-2361
29. Monajjemi, M. Chemical Physics. 2013, 425, 29-45
30. Monajjemi, M.; Heshmat, M.; Aghaei, H.; Ahmadi, R.; Zare, K. Bulletin of the Chemical Society of Ethiopia, 2007, 21 (1)
31. Monajjemi, M.; Honarparvar, B. H. ; Haeri, H. ; Heshmat ,M.;  Russian Journal of  Physical Chemistry C. 2006, 80(1):S40-S44
32. Monajjemi, M.; Ketabi, S.; Amiri, A. Russian Journal of Physical Chemistry, 2006, 80 (1), S55-S62
33. Yahyaei, H.; Monajjemi, M.; Aghaie, H.; K. Zare, K. Journal of Computational and Theoretical Nanoscience. 2013, 10, 10, 2332–2341
34. Mollaamin, F.; Gharibe, S.; Monajjemi, M. Int. J. Phy. Sci, 2011, 6, 1496-1500
35. Monajjemi, M.; Ghiasi, R.; Seyed Sadjadi, M.A. Applied Organometallic Chemistry,2003, 17, 8, 635–640
36. Monajjemi, M.; Wayne Jr, Robert. Boggs, J.E.  Chemical Physics. 2014, 433, 1-11
37. Monajjemi, M.; Sobhanmanesh, A.; Mollaamin, F. Fullerenes, Nanotubes, and Carbon Nanostructures, 2013, 21 47–63
38. Monajjemi, M.; Mollaamin, F. Journal of Computational and Theoretical Nanoscience, 2012, 9 (12) 2208-2214
39. Monajjemi, M.; Honarparvar, B.; Nasseri, S. M. .; Khaleghian M. Journal of Structural Chemistry. 2009, 50, 1, 67-77
40. Monajjemi, M.; Aghaie, H.; Naderi, F. Biochemistry (Moscow).2007, 72 (6), 652-657
41. Ardalan, T.; Ardalan, P.; Monajjemi, M. Fullerenes, Nanotubes, and Carbon Nanostructures, 2014, 22: 687–708
42. Mollaamin, F.; Monajjemi, M.; Mehrzad, J. Fullerenes, Nanotubes, and Carbon Nanostructures. 2014, 22: 738–751
43. Monajjemi, M.; Najafpour, J.; Mollaamin, F. Fullerenes, Nanotubes, and Carbon Nanostructures. 2013, 21(3), 213–232
44. Monajjemi, M.;  Karachi, N.; Mollaamin, F.  Fullerenes, Nanotubes, and Carbon Nanostructures, 2014, 22: 643–662
45. Yahyaei, H.; Monajjemi, M. Fullerenes, Nanotubes, and Carbon Nanostructures.2014, 22(4), 346–361
46. Monajjemi, M. Falahati, M.; Mollaamin, F.; Ionics, 2013, 19, 155–164
47. Monajjemi, M.; Mollaamin, F. Journal of Cluster Science, 2012, 23(2), 259-272
48. Tahan, A.; Monajjemi, M. Acta Biotheor, 2011, 59, 291–312
49. Lee, V.S.; Nimmanpipug, P.; Mollaamin, F.; Kungwan, N.; Thanasanvorakun, S..; Monajjemi, M.  Russian Journal of Physical Chemistry A, 2009, 83, 13, 2288–2296
50. Monajjemi, M.; Heshmat, M.; Haeri, HH, Biochemistry (Moscow), 2006, 71 (1), S113-S122
51. Monajjemi, M.; Yamola, H.; Mollaamin, F. Fullerenes, Nanotubes, and Carbon Nanostructures, 2014, 22, 595–603
52. Mollaamin, F.; Layali, I.; Ilkhani A. R.; Monajjemi, M.  African Journal of Microbiology Research .2010, 4(24) 2795-2803
53. Mollaamin, F.; Shahani poor, p K. .; Nejadsattari, T.  ; Monajjemi, M. African Journal of Microbiology Research. 2010, 4(20) 2098-2108
54. Monajjemi, M.; Ahmadianarog, M. Journal of Computational and Theoretical Nanoscience. 2014,   11(6), 1465-1471
55. Monajjemi, M.; Jafari Azan, M.; Mollaamin, F. Fullerenes, Nanotubes, and Carbon Nanostructures.2013, 21(6), 503–515
56. Mollaamin, F.; Monajjemi, M. Physics and Chemistry of Liquids .2012, 50,  5,  2012, 596–604
57. Monajjemi, M.; Khosravi, M.; Honarparvar, B.; Mollaamin, F.; International Journal of Quantum Chemistry, 2011, 111, 2771–2777
58. Khaleghian, M.; Zahmatkesh, M.; Mollaamin, F.; Monajjemi, M.  Fullerenes, Nanotubes, and Carbon Nanostructures, 2011, 19(4): 251–261
59. Monajjemi, M.; Baheri, H.; Mollaamin, F.  Journal of Structural Chemistry.2011 52(1), 54-59
60. Mahdavian, L.; Monajjemi, M.; Mangkorntong, N. Fullerenes, Nanotubes and Carbon Nanostructures, 2009, 17 (5), 484-495
61. Monajjemi, M., Mahdavian, L., Mollaamin, F. Bull. Chem. Soc. Ethiop. 2008, 22(2), 277-286
62. Monajjemi, M.; Afsharnezhad, S, Jaafari, M.R..; Mirdamadi, S..; Mollaamin, F..; Monajemi, H. Chemistry .2008, 17 (1), 55-69
63. Monajjemi, M.; Mollaamin, F.; Gholami, M. R.; Yoozbashizadeh, H.;  Sadrnezhaad, S.K.; Passdar, H.;  Main Group Metal Chemistry, 2003, 26, 6, 349-361
64. Monajjemi, M.; Azad ,MT.; Haeri, HH.; Zare, K.; Hamedani, Sh.; JOURNAL OF CHEMICAL RESEARCH-S.2003, (8): 454-456
65. Monajjemi, M.; Najafpour, J. Fullerenes, Nanotubes, and Carbon Nanostructures, 2014, 22(6): 575–594
66. Monajjemi, M.; Noei, M.; Mollaamin, F. Nucleosides, Nucleotides and Nucleic Acids. 2010 29(9):676–683
67. Ghiasi, R.; Monajjemi, M.  Journal of Sulfur Chemistry .2007, 28, 5, 505-511
68. Monajjemi, M.; Ghiasi, R.; Abedi, A. Russian Journal of Inorganic Chemistry.2005, 50(3), 382-388
69. Monajjemi, M. .; Naderi, F.; Mollaamin, F.; Khaleghian, M.  J. Mex. Chem. Soc. 2012, 56(2), 207-211
70. Monajjemi, M.; Farahani, N.; Mollaamin, F.  Physics and Chemistry of Liquids, 2012, 50(2) 161–172
71. Monajjemi, M.; Seyed Hosseini, M. Journal of Computational and Theoretical Nanoscience .2013, 10 (10), 2473-2477
72. Monajjemi , M.;  Honaparvar , B.; Khalili Hadad ,B.; Ilkhani ,AR.; Mollaamin, F. African Journal of Pharmacy and Pharmacology .2010, 4(8), 521 -529
73. Monajjemi, M.  Theor Chem Acc, 2015, 134:77 DOI 10.1007/s00214-015-1668-9
74. Monajjemi, M.  Journal of Molecular Modeling , 2014, 20, 2507
75. Monajjemi , M.; Honarparvar, B.; Monajemi, H.;. Journal of the Mexican Chemical Society, 2006, 50 (4), 143-148
76. Monajjemi, M.; Khaleghian, M.; Mollaamin, F.   Molecular Simulation. 2010, 36, 11,  865–
77. Ilkhani, Ali R.; Monajjemi, M. Computational and Theoretical Chemistry.2015 1074, 19–25
78. Monajjemi, M.  Biophysical Chemistry. 2015 207,114 –127
79. Monajjemi, M., Moniri, E., Panahi, H.A , Journal of Chemical and Engineering Data.2001, 1249-1254.
80. Mollaamin, F.; Najafpour, J.; Ghadami, S.; Ilkhani, A. R.; Akrami, M. S.; Monajjemi, M. Journal of Computational and Theoretical Nanoscience. 11 (5), 1290-1298
81. Monajjemi, M.; Ghiasi, R.; Ketabi, S.; Passdar, H.; Mollaamin, F. Journal of Chemical Research . 2004, 1, 11.
82. Monajjemi, M.; Heshmat, M.; Haeri, H.H. Biochemistry (Moscow).2006, 71, 113-122
83. Monajjemi, M.; Heshmat, M.; Aghaei, H.;Ahmadi, R.; Zare, K. Bulletin of the Chemical Society of Ethiopia. 2007, 21, 111–116
84. Monajjemi, M., Kharghanian, L., Khaleghian, M., Chegini, H. Fullerenes Nanotubes and Carbon Nano structures.2014, 22, 8, 0.1080/1536383X.2012.717563
85. Sarasia, E.M.; Afsharnezhad, S.; Honarparvar, B.; Mollaamin, F.; Monajjemi, M. Physics and Chemistry of Liquids. 2011, 49 (5), 561-571
86. Amiri, A.; Babaeie, F.; Monajjemi, M. Physics and Chemistry of Liquids. 2008, 46, 4, 379-389
87. Monajjemi, M.; Heshmat, M.; Haeri, H.H.; Kaveh, F. Russian Journal of Physical Chemistry A, 2006, 80, 7, 1061-1068
88. Monajjemi, M.; Moniri, E.; Azizi, Z.; Ahmad Panahi, H. Russian Journal of Inorganic Chemistry. 2005, 50, 1, 40-44
89. Jalilian,H.; Monajjemi, M. Japanese Journal of Applied Physics. 2015, 54, 8, 08510
90. Mollaamin, F.; Monajjemi, M. Journal of Computational and Theoretical Nanoscience. 2015, 12, 6, 1030-1039
91. Felegari, Z.; Monajjemi, M. Journal of Theoretical and Computational Chemistry. 2015, 14, 3, 1550021
92. Shojaee, S., Monajjemi, M. Journal of Computational and Theoretical Nanoscience. 2015, 12, 3, 449-458
93. Esmkhani, R.; Monajjemi, M. Journal of Computational and Theoretical Nanoscience. 2015. 12, 4, 652-659
94. Monajjemi, M., Seyedhosseini, M., Mousavi, M., Jamali, Z. Journal of Computational and Theoretical Nanoscience. 2015 , 23 (3), 239-244
95. Ghiasi, R.; Monajjemi, M.; Mokarram, E.E.; Makkipour, P. Journal of Structural Chemistry. 2008, 4 , 4, 600-605
96. ahdavian, L.; Monajjemi, M. Microelectronics Journal. 2010, 41(2-3), 142-149
97. Monajjemi, M.; Baie, M.T.; Mollaamin, F. Russian Chemical Bulletin.2010, 59, 5, 886-889
98. Bakhshi, K.; Mollaamin, F.; Monajjemi, M. Journal of Computational and Theoretical Nanoscience. 2011, 8, 4, 763-768
99. Darouie, M.; Afshar, S.; Zare, K., Monajjemi, M. journal of Experimental Nanoscience.2013, 8, 4, 451-461
100. Amiri, A.; Monajjemi, M.; Zare, K.; Ketabi, S. Physics and Chemistry of Liquids. 2006, 44, 4, 449-456.
101. Zonouzi, R.;Khajeh, K.; Monajjemi, M.; Ghaemi, N. Journal of Microbiology and Biotechnology. 2013, 23, 1 ,7-14
102. Ali R. Ilkhani .; Majid Monajjemi, Computational and Theoretical Chemistry.2015, 1074 19–25
103. Tahan, A.; Mollaamin, F.;  Monajjemi, M. Russian Journal of Physical Chemistry A, 2009, 83 (4), 587-597
104. Khalili Hadad, B.;  Mollaamin, F.;  Monajjemi, M, Russian Chemical Bulletin,2011, 60(2):233-236\
105. Mollaamin, F.;  Monajjemi, M.;  Salemi, S.;  Baei, M.T. Fullerenes Nanotubes and Carbon Nanostructures, 2011, 19, 3, 182-196
106. Mollaamin, F.;  Shahani Pour.;  K., Shahani Pour, K.; ilkhani, A.R.;  Sheckari, Z., Monajjemi, M Russian Chemical Bulletin , 2012 , 61(12), 2193-2198
107. Shoaei, S.M.; Aghaei, H.; Monajjemi, M.; Aghaei, M. Phosphorus, Sulfur and Silicon and the Related Elements. 2014, 189, 5; 652-660
108. Mehrzad, J., Monajjemi, M., Hashemi, M , Biochemistry (Moscow).2014 , 79 (1), 31-36
109. Moghaddam, N.A., Zadeh, M.S., Monajjemi, M. Journal of Computational and Theoretical Nanoscience , 2015 , Vol. 12, No. 3, doi:10.1166/jctn.2015.3736
110. Joohari, S.; Monajjemi, M , Songklanakarin Journal of Science and Technology , 2015 , 37(3):327
111. Rajaian, E., Monajjemi, M., Gholami, M.R, Journal of Chemical Research – Part S ,2002, 6, 1, 279-281
112. Ghassemzadeh, L., Monajjemi, M., Zare, K , Journal of Chemical Research – Part S, 2003, 4, 195-199
113. Maryam Mehdizadeh Barforushi, Soodeh Safari, and Majid Monajjemi J. Comput. Theor. Nanosci. 12, 3058-3065 (2015)
114. Fatemeh Mollaamin, Alireza Ilkhani, Neda Sakhaei, Behnaz Bonsakhteh, Afsaneh Faridchehr, Sogand Tohidi, and Majid Monajjemi J. Comput. Theor. Nanosci. 12, 3148-3154 (2015)
115. Hassan Rahmati and Majid Monajjemi J. Comput. Theor. Nanosci. 12, 3473-3481 (2015)
116. Roghieh Tarlani Bashiz and Majid Monajjemi J. Comput. Theor. Nanosci. 12, 3808-3816 (2015)
117. Akbar Mehrabi Nejad and Majid Monajjemi J. Comput. Theor. Nanosci. 12, 3902-3910 (2015)
118. Majid Monajjemi *, Samira Bagheri, Matin S. Moosavi, Nahid Moradiyeh, Mina Zakeri, Naime Attarikhasraghi, Nastaran Saghayimarouf, Ghorban Niyatzadeh, Marzie Shekarkhand, Mohammad S. Khalilimofrad, Hashem Ahmadin and Maryam Ahadi, Molecules 2015, 20, 21636–21657; doi:10.3390/molecules201219769
119. Elham Shabanzadeh and Majid Monajjemi, J. Comput. Theor. Nanosci. 12, 4076-4086 (2015)
120. Akbar Elsagh, Hamidreza Jalilian, Elham Kianpour, Hediyeh Sadat Ghazi Mokri, Mostafa Rajabzadeh, Matin Sadat Moosavi, Fateme Ghaemi Amiri, and Majid Monajjemi J. Comput. Theor. Nanosci. 12, 4211-4218 (2015)
121. Afsaneh Faridchehr, Abdolhossein Rustaiyan, and Majid Monajjemi J. Comput. Theor. Nanosci. 12, 4301-4314 (2015)
122. Sogand Tohidi, Majid Monajjemi, and Abdolhossein RustaiyanJ. Comput. Theor. Nanosci. 12, 4345-4351 (2015)
123. Mahsa Ali Akbari Zadeh, Hadi Lari, Leyla Kharghanian, Ebrahim Balali, Ramona Khadivi, Hooriye Yahyaei, Fatemeh Mollaamin, and Majid Monajjemi J. Comput. Theor. Nanosci. 12, 4358-4367 (2015)
124. Sahar Dezfooli, Hadi Lari, Ebrahim Balali, Ramona Khadivi, Farand Farzi, Nahid Moradiyeh, and Majid Monajjemi J. Comput. Theor. Nanosci. 12, 4478-4488 (2015)
125. Hamidreza Jalilian, Masoumeh Sayadian, Akbar Elsagh, Farand Farzi, Nahid Moradiyeh, Neda Samiei Soofi, Somayeh Khosravi, Nayyer T. Mohammadian, and Majid Monajjemi J. Comput. Theor. Nanosci. 12, 4785-4793 (2015)
126. Farand Farzi, Samira Bagheri, Mostafa Rajabzadeh, Masoumeh Sayadian, Hamidreza Jalilian, Nahid Moradiyeh, and Majid Monajjemi J. Comput. Theor. Nanosci. 12, 4862-4872 (2015)
127. Majid Monajjemi and Nayyer T. Mohammadian J. Comput. Theor. Nanosci. 12, 4895-4914 (2015)
128. Monajjemi, M., Chahkandi, B. Journal of Molecular Structure: THEOCHEM, 2005, 714 (1), 28, 43-60.
129. A. Loiseau, F.  Willaime, N. Demoncy, G. Hug and  H. Pascard  , Phys.  Rev.  Lett. 76 4737, (1996)
130. K. H. Khoo, M.  S.  C. Mazzoni and S. G. Louie, Phys. Rev. B 69, 201401R, (2004)
131. Y. Miyamoto, A. Rubio , M.L. Cohen and S. G. Louie, Phys. Rev. B 50   , 4976, (1994)
132. E. J. Mele and P. Kral, Phys.  Rev. Lett. 88, 56803, (2002)
133. S. M. Nakhmanson, A. Calzolari,V. Meunier, J. Bernholc and M. B. Nardelli  Phys.  Rev. B 67, 235406, (2003)
134. X. Bai, D. Golberg, Y. Bando, C. Zhi, C. Tang, M. Mitome and K. Kurashima  Nano Lett. 7 632, (1997)
135. Lu T, Chen F (2011), Acta Chim. Sinica, 69, 2393-2406
136. Lu T, Chen F (2012) , J. Mol. Graph. Model (38): 314-323
137. Lu T, Chen F (2012) Multiwfn: A Multifunctional Wavefunction Analyzer, J. Comp. Chem. (33) 580-592
138. M.W.Schmidt, K.K.Baldridge, J.A.Boatz, S.T.Elbert, M.S.Gordon, J.H.Jensen, S.Koseki, N.Matsunaga, K.A.Nguyen et al 14(11) 1347–1363, (2004)
139. L.E. Chirlian , M.M. Francl, J.comp.chem.8 ,894, (1987)
140. Brneman GM, Wiberg KB, J. Comp Chem (11): 361, (1990)
141. Martin F, Zipse H Charge distribution in the water molecule–a comparison of methods. J Comp Chem. (26): 97 – 105, (2005)
142. Naghsh,F, orient.j.chem, 2015, 31(1).,465-478
143. Chitsazan, A, orient.j.chem, 2015, 31(1).,393-408

---

This work is licensed under a Creative Commons Attribution 4.0 International License.