Structure and Nonlinear Optical Properties Study of  2-amino-5-chlorobenzophenone: A Spectroscopic Approach

Introduction

Benzophenone, an aromatic ketone (diphenylketone), is an important compound in organic photochemistry which is used as a constituent of synthetic perfumes and as a starting material for the manufacture of dyes, pesticides and drugs and also used as a photo initiator of UV-curing applications in inks, adhesive and coatings, optical fiber as well as in printed circuit boards.  It has been the object of many spectral, structural and theoretical investigations because of its interesting chemical and physical properties. Further, the crystals of benzophenones are found to be useful materials for the fabrication of nonlinear optical devices ^1,2. A number of benzophenone derivatives show significantly high second harmonic generation conversion efficiency ^3-5.

The present study deals with the vibrational analysis of 2-amino-5-chlorobenzophenone (2A-5CB) using density functional theory (DFT) calculations ⁶ to elucidate the correlation between the molecular structure, nonlinear optical (NLO) property, charge transfer interactions, and first-order hyperpolarizability.

Materials and Methods

The commercially available 2A-5CB (C₁₃H₁₀ClNO) was purified by repeated recrystallization process using ethanol. Since the solubility of 2A-5CB is high (10.65 gm/100 ml of ethanol at 35°C) in ethanol, it is easy to grow good quality single crystal. The seed crystals were obtained after three days, among them the defect free and perfectly shaped ones with high transparency were used as the seed crystals for further growth experiment. The seed crystals were first seasoned in the mother solution taken in the Mason jar crystallizer using nylon thread and then allowed to grow into bigger size. The jar was covered with perforated lid to facilitate the slow evaporation of the solvent at a constant temperature of 305K. Single crystals of size 14 x 6 x 5 mm³ are grown in a period of 50-60 days. The crystals tend to grow as needles and appear dark gold in color with good transparency.

The room temperature  FTIR spectra of the title compound was recorded  in the region 4000-400 cm^–1 at a resolution of ±1 cm^–1, using Bruker IFS 66V vacuum Fourier transform spectrometer, a KBr beam splitter and  globar source. The FT-Raman spectra were recorded on the same instrument with FRA 106 Raman accessories in the region 3500-50 cm⁻¹. Nd:YAG laser operating at 200 mW power with 1064 nm excitation source.

DFT performed using Gaussian’09 program ⁷ at the B3LYP level ^8,9, with 6-31G(d) basis set has been used to compute molecular structure and vibrational wave numbers. For the plots of simulated IR and Raman spectra, pure Lorentzian band shapes were used with full width at half maximum band width of 10 cm^-1. The calculated Raman activities were converted to relative Raman intensities using the following relationship derived from the basic theory of Raman scattering ^10,11.

where,  ν_o is the exciting frequency (in cm^-1), ν_i the vibrational wavenumber of the i^th normal mode, h, c and k, the universal constants and f  is the suitably chosen common  scaling factor for all the peak intensities.

Results and Discussion

Molecular geometry study

The optimized molecular structure of 2A-5CB was calculated at B3LYP/6-31G(d) level of theory. The optimized molecule structure is shown in Fig. 1. The geometrical parameters are tabulated in Table 1.

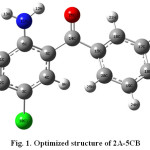Figure 1: Optimized structure of 2A-5CB   Click here to View figure

 

Table 1: The optimized geometrical parameters of 2A-5CB at DFT level of theory

Bond length (Å)		Bond angles (º)		Dihedral angles (º)
Parameters	value	Parameters	value	Parameters	value
C1-C2	1.383	C1-C2-C3	119.6	C1-C2-C3-C4	1.2
C2-C3	1.400	C2-C3-C4	120.2	C2-C3-C4-C5	-0.25
C3-C4	1.383	C3-C4-C5	121.3	C3-C4-C5-C6	-1.87
C4-C5	1.459	C4-C5-C6	118.8	C3-C2-C1-H7	179.16
C5-C6	1.410	C2-C1-H7	119.6	C4-C3-C2-H8	-179.61
C1-H7	1.087	C3-C2-H8	120.0	C2-C3-C4-H9	-178.69
C2-H8	1.085	C3-C4-H9	119.3	C1-C2-C3-Cl10	-178.55
C4-H9	1.082	C2-C3-Cl10	119.7	C4-C5-C6-N11	-179.26
C3-Cl10	1.762	C5-C6-N11	121.9	C5-C6-N11-H12	18.51
C6-N11	1.365	C6-N11-H12	116.3	C5-C6-N11-H13	168.67
N11-H12	1.013	C6-N11-H13	118.2	C3-C4-C5-C14	-178.62
N11-H13	1.009	C4-C5-C14	120.6	C4-C5-C14-C15	-20.89
C5-C14	1.483	C5-C14-C15	120.9	C5-C14-C15-C16	145.84
C14-C15	1.502	C14-C15-C16	117.8	C14-C15-C16-C17	176.83
C15-C16	1.403	C15-C16-C17	120.5	C15-C16-C17-C18	-1.55
C16-C17	1.391	C16-C17-C18	120.1	C16-C17-C18-C19	0.05
C17-C18	1.398	C17-C18-C19	119.9	C17-C18-C19-C20	1.05
C18-C19	1.395	C18-C19-C20	120.1	C18-C17-C16-H21	178.33
C19-C20	1.395	C17-C16-H21	120.8	C19-C18-C17-H22	179.55
C16-H21	1.085	C18-C17-H22	120.1	C16-C17-C18-H23	-179.51
C17-H22	1.086	C17-C18-H23	120.1	C17-C18-C19-H24	-178.79
C18-H23	1.086	C18-C19-H24	120.2	C18-C19-C20-H25	-178.94
C19-H24	1.086	C19-C20-H25	119.7	C16-C15-C14-O26	-34.25
C20-H25	1.085	C15-C14-O26	117.7
C14-O26	1.237

 

The dihedral angle C₅-C₆-N₁₁-H₁₂ of the amino group with the phenyl ring 1 shows a deviation of 18.51° from the plane of the ring. The internal bond angle at the carbon atom to which amino group attached (C₁-C₆-C₅=118.286 Å) is consistently smaller than the normally adopted internal bond angle of the phenyl ring. The tri-substituted benzene ring appears a little distorted with C₅-C₆ and C₁-C₆ bond lengths 1.43118 and 1.41395 Å,  respectively exactly at the amino group substitution which are longer than C₃-C₄, C₂-C₃ and C₁-C₂ bond lengths 1.3831, 1.40 and 1.3853 Å, respectively. These indicate the resonance effect between the amino group and the phenyl ring1. The bond angle of carbon atom attached to the chlorine atom (C₂-C₃-C₄=120.24 Å) exceeds the normal value 120^o. This is due to the electron donating nature of the chlorine atom.

Conjugation of carbonyl group with the phenyl rings would favour a planar conformation, but the steric repulsion between the two ortho hydrogen atoms H₉ and H₂₅ prevents the attainment of co-planarity ¹². The two phenyl rings of 2A-5CB are non-planar with C₆-C₅-C₁₄-C₁₅ (162.42 Å) and C₅-C₁₄-C₁₅-C₁₆ (145.84 Å) dihedral angles. This behaviour has been observed in many structural and spectroscopic studies of diphenyl compounds ¹³. The C₅-C₁₄ (1.483) and C₁₄-C₁₅ (1.5027 Å) are slightly larger than other C-C bonds, indicating negligible conjugation interaction between the two phenyl ring systems. The short inter-atomic distance N_11-H₁₂^…O₂₆ reveals the possibility of intramolecular hydrogen bonding.

Potential energy surface scan study

In order to reveal the minimum energy conformation of the compound, the detailed potential energy surface scan of the dihedral angle C₅-C₁₄-C₁₅-C₁₆ is performed. The scan has been carried out by minimizing the potential energy in all geometrical parameters by changing the torsion angle for every 10° for a 360° rotation. The shape of the potential energy as a function of the dihedral angle is illustrated in Fig. 2.

Figure 2: Potential energy surface scan curve for the dihedral angle C5-C14-C15-C16   Click here to View figure

 

The structural studies of tri-substituted benzophenone show approximately equal twist angles of each ring in the range of 20-35°. Hence, a subsequent geometry optimization calculation was carried out by allowing the rotation around the two phenyl rings. From the Fig. 2, it can be shown that the global minimum is observed at 30°. The global minimum energy obtained to be -1091.61 kJ mol^-1.

Natural bond orbital analysis

The natural bond orbital (NBO) analysis provides a description of the structure of a conformer by a set of localized bond, antibonds and Rydberg extra valence orbitals. Stabilizing interactions between filled and unoccupied orbitals and destabilizing interactions between filled orbitals can also be obtained from this analysis ^14-16. Therefore, NBO theory is a valuable complement to the energetic and structural data. DFT level computation is used to investigate the various second order interactions between the filled orbitals of one subsystem and the vacant orbitals of another subsystem, which is a measure of delocalization or hyperconjugation ¹⁷. The main natural orbital interactions were analyzed with the NBO 3.1 program ¹⁸. The hyperconjugative interaction energy was deduced from the second-order perturbation approach.

 

where, <σ|F|<σ², or F²_ij is the Fock matrix element between i and j NBO orbitals, ε_s andε_s*  are the energies of s and σ* NBO’s, and σ_s is the population of the donor s orbital.  NBO theory can also be used to identify the hydrogen bonding.

The lowering of orbital energy due to the interaction between doubly occupied orbitals and unoccupied ones is a convenient guide to interpret the molecular structure in the electronic point of view. In energetic terms, hyperconjugation is an important effect in which an occupied Lewis-type natural bond orbital is stabilized by overlapping with a non Lewis-type orbital (either one-center Rydberg or two-center antibonding NBO). This electron delocalization can be described as a charge transfer from a Lewis valence orbital (donor), with a decreasing of its occupancy, to a non-Lewis orbital (acceptor). NBO analysis of 2A-5CB has been performed in order to elucidate the bond effect, intramolecular N-H^…O hydrogen bonding and hyperconjugative interaction and the results are shown in the Tables 2 and 3.

Table 2: NBO result showing the formation of Lewis and non-Lewis orbitals by the valance hybrids corresponding to the intramolecular N-H^…O

Bond(A-B)	ED (a.u)	EDA%	EDB %	NBO	S%	P%
π C18-C19	1.6527 -0.2495	49.18 –	50.82 –	0.7013(sp1.00)C 0.7129(sp1.00)C	0.00 0.00	99.96 99.96
π C16-C17	1.6559 -0.2481	48.56 –	51.44 –	0.7081(sp1.81)C 0.7061(sp1.83)C	35.58 35.26	64.38 64.70
π C15-C20	1.6450 -0.2499	51.86 –	48.14 –	0.7202(sp99.99)C 0.6938(sp99.99)C	0.01 0.03	99.96 99.93
π C14-O26	1.9691 -0.3686	31.44 –	68.56 –	0.5607(sp99.99)C 0.8280(sp99.99)O	0.03 0,04	99.80 99.68
π C5-C6	1.5731 -0.2473	58.78 –	41.22 –	0.7667(sp99.99)C 0.6420(sp1.00)C	0.01 0.00	99.98 99.96
π C1-C2	1.7277 -0.2608	53.90 –	46.10 –	0.7342 (sp1.00)C 0.6790(sp1.00)C	0.00 0.00	99.96 99.94
π C3-C4	1.7225 -0.2702	56.06 –	43.94 –	0.7488(sp1.00)C 0.6628(sp1.00)C	0.00 0.00	99.98 99.95
π*C3-C4	0.3687 0.0194	43.94 –	56.06 –	0.6628(sp1.00)C -0.7488(sp1.00)C	0.00 0.00	99.98 99.95
π*C1-C2	0.3039 0.0282	46.10 –	53.90 –	0.6790 (sp1.00)C -0.7342 (sp1.00)C	0.00 0.00	99.96 99.94
π*C5-C6	0.4642 0.0191	41.22 –	58.78 –	0.6420(sp99.99)C -0.7667(sp1.00)C	0.01 0.00	99.98 99.96
π*C16-C17	0.2970 –  0.0363	51.44	48.56	0.7172 (sp1.00)C -0.6969 (sp1.00)C	0.00  0.00	99.95 99.96
π*C15-C20	0.3658 0.0313	48.14 –	51.86 –	0.6938(sp99.99)C -0.7202(sp99.99)C	0.01 0.03	99.96 99.93
π*C14-O26	0.2133 0.0092	68.56 –	31.44 –	0.8280 (sp99.99)C -0.5607(sp99.99)O	0.03 0.04	99.80 99.68
π*C18-C19	0.3213 0.0319	50.82 –	49.18 –	0.7129 (sp1.00)C -0.7013 (sp1.00)C	0.00 0.00	99.96 99.96
π*N11-H12	0.03183	26.84	73.16	0.5181 (sp2.3)N	30.3	69.64

 

The N-H^…O hydrogen bonding, in NBO terms, corresponds to the oxygen lone pair and the electron transfer from LP oxygen to the antibonding (N-H) orbital. The energy lowering corresponding to the interaction between a filled orbital (i) and an antibonding orbital (j*), is deduced from the second-order perturbation of the filled orbital. Among the most energetic donor–acceptor NBO interactions are those involving the p-type lone pair of the oxygen atom, LP₂O₂₆ with vicinal σ*(N₁₁-H₁₂) antibonds having energy contribution 32.3 kJ mol^-1 of hyperconjugative interaction is weak, these E(2) values and the low value electron density (0.5181e) are chemically significant and can be used as a measure of the intramolecular delocalization. The energy values corresponding to the charge transfer in the molecules are formed by hydrogen bonding.

Table 3: Second order perturbation theory analysis of Fock matrix in NBO basis

Donor NBO (i)	ED (i) e	Acceptor NBO (j)	ED (j) e	E(2) kJ/ mola	E(j)-E(i) kJ/ mola	F (i,j) kJ/ mola
π (C1-C2)	1.7277	π* (C3-C4)	0.36870	62.5	735.1	154.9
		π*(C5-C6)	0.46418	90.9	735.1	191.7
π (C3-C4)	1.7225	π*(C1-C2)	0.30394	92	787.7	191.7
		π*(C5-C6)	0.46418	52.1	761.4	147
π (C5-C6)	1.5731	π*(C1-C2)	0.30394	58.7	735.1	149.7
		π*(C3-C4)	0.36870	113.2	708.9	202.2
π (C15-C20)	1.6450	π*(C14-C26)	0.21333	59.5	682.6	147
		π*(C16-C17)	0.29702	82.2	761.4	178.5
		π*(C18-C19)	0.32134	79.9	735.1	173.3
π (C16-C17)	1.6559	π*(C15-C20)	0.36582	81.3	735.1	173.3
		π*(C18-C19)	0.32134	88.6	735.1	181.2
π (C18-C19)	1.6527	π*(C15-C20)	0.36582	89.8	735.1	183.8
		π*(C16-C17)	0.29702	77.2	761.4	173.3
LP1 N11	1.7538	π*(C5-C6)	0.46418	180.7	761.4	275.7
LP2 O26	1.8851	σ*(C5-C14)	0.05521	62.8	1916.6	249.4
		σ*(C14-C15)	0.05987	77.9	1837.9	273.1
		σ*(N11-H12)	0.03183	32.3	1995.4	183.8
LP3 Cl10	1.9427	π*(C3-C4)	0.36870	46.52	866.6	154.9

^aE(2) means energy of hyperconjugative interactions (stabilization energy)

^bEnergy difference between donor and acceptor i and j NBO orbitals

^cF(i, j) is the Fock matrix element between i and j NBO orbitals

The intramolecular hyperconjugative interactions are formed by the orbital overlap between π(C-C) and π*(C-C) bond orbitals, which results in intramolecular charge transfer (ICT) causing stabilization of the system. These interactions are observed as an increase in ED in C-C anti-bonding orbital that weakens their respective bonds. The ED at the six conjugated π(C-C) bonds (1.6-1.7e) and π* bonds (0.213-0.464e) of the phenyl rings clearly demonstrate strong delocalization of electrons leading to a stabilization of energy (80-90 kJ mol^-1). This is due to intramolecular charge transfer interaction inside the ring. Among the most energetic donor-acceptor NBO interactions are those involving the p-type lone pair of the oxygen atom, LP₁N₁₁ with π*(C₅-C₆) antibonds and, LP₃Cl₁₀ with π*(C₃-C₄) having energy contributions 180.71 and 46.52 kJ mol^-1, respectively of hyperconjugative interaction are chemically significant and can be used as a measure of the intramolecular delocalization. A strong interaction has also been observed between the p type orbital containing the lone electron pair of O₂₆ and the neighbourhood anti-bonding orbitals σ*(C₅-C₁₄) and σ*(C₁₄-C₁₅), respectively. This interaction is responsible for hyperconjugation between O₂₆ and the ring. These ICT results support the nonlinear optical activity of the molecule.

Vibration spectral analysis                                

The observed and calculated wavenumbers together with the calculated IR and Raman intensities are assigned based on potential energy distributions (PED) using VEDA4 program ¹⁹, which are given in table 4. The observed and simulated vibrational spectra are presented in Figs. 3 and 4. The spectra consists of  vibrational  patterns originating from the mono and tri-substituted benzene rings and also the spectral lines corresponding to CO, NH₂ and CCl group vibrations that are discussed.

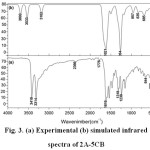Figure 3: (a) Experimental (b) simulated infrared spectra of 2A-5CB  Click here to View figure

 

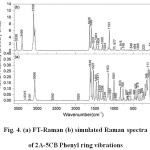Figure 4: (a) FT-Raman (b) simulated Raman spectra of 2A-5CB   Click here to View figure

 

Phenyl ring vibrations

2A-5CB consists of an asymmetrically tri-substituted (Ph₁) and a mono-substituted benzene ring (Ph₂). The various normal modes of vibrations of these rings are assigned according to Wilson’s numbering convention ^20,21 which are well shown in the calculated DFT level.

An asymmetric tri-substituted aromatic system (Ph₁) has two adjacent and one isolated C-H moieties. The hetero aromatic structure shows the presence of C-H stretching vibrations in the region 3100-3000 cm^-1, which is the characteristic region for the ready identification of C-H stretching vibration which are 2, 20a and 20b modes. Only ring mode 2 is observed in Raman as a weak band at 3191 cm^-1 (PED 99%). The bands 20a and 20b are absent or mixed with other bands and cannot be distinctly observed. These wavenumbers do not correlate with the experimental band position and can be substituted to the intermolecular non bonded interactions. Also ring modes are found to be sensitive to other interactions and the shifting of band position of these modes can be observed. In the case of mono-substituted phenyl ring (Ph₂), there are five C-H stretching vibrations active. They are 2,7a,7b,20a and 20b, which fall in the region 3120-3010 cm^{-1 22}. The weak shoulder band in IR at 3063 cm^-1 and the strong band at 3066 cm^-1 in Raman are assigned to the 20a mode, the PED being 87%. Several C-H stretching modes are found to be weak, which are due to the charge transfer between the hydrogen atoms and the carbon atoms ²³.

Table 4: Vibrational assignments of 2A-5CB based on potential energy distribution method

Assignment with PED (%)c
	υcal cm-1	Relative Intensity		υIR cm-1	υRaman cm-1
IR		Raman
3538	63	2	3418 vs	–	NH2 asy str(100)
3396	94	5	3314 vs	3315m	NH2 sym str(100)
3117	1	1	–	3191w	mode 2 of ring 1(99)
3098	7	4	–	–	mode 2e of ring2(95)
3097	7	5	–	–	mode 2 of ring 1(95)
3092	12	3	–	–	mode20a of ring 2(80)
3083	29	3	–	–	mode 20a of ring 2(87)
3073	10	4	–	–	mode 7b of ring 2(88)
3063	0	1	3063 w sh	3066vs	mode 20a of ring 2(87)
3061	16	3	–	–	mode 20a of ring 1 (95)
1638	110	18	1616 vs	1617vs	NH2 sci(11),C=Ostr(69)
1609	202	4	–	–	mode 8a of ring 1(44),NH2 sci(25)
1594	8	21	–	1596vs	mode 8a of ring 2(61)
1574	116	1	–	1575sh	NH2 rocking(22),mode 8b of ring 2(16)
1570	98	2	–	–	mode 8b of ring 2(24)
1534	112	9	1536 vs	1537vs	mode 19b of ring 1(27)
1479	3	1	–	–	mode 19a of ring 2(73)
1459	59	11	1466 w	1464s	mode 19a of ring 1(45)
1434	10	1	–	–	mode 19a of ring 2(63)
1398	17	6	1405 m	1410s	mode 14 of ring 1(59)
1326	11	3	–	1359m	mode 14 of ring 1(69)
1314	3	0	1318 s	–	mode 3 of ring 2(79)
1300	26	7	–	–	mode 3 of ring 1(63)
1295	17	1	1291 sh	1296m	mode 3 of ring 2(42),mode 3 of ring 1(29)
1275	89	1	–	–	mode 3 of ring 1(50)
1228	337	2	1238 s	1237w	C4-C5 str(11), C5-C14 str(29),H9-C4-C5 bend(22)
1167	23	1	1181 m	–	mode 9a of ring 2(89)
1149	4	3	–	–	mode 15 of ring 1(56),  mode 15 of ring 2(12)
1148	29	2	1150 m	1153 vs	mode 9b of ring 1(56),mode 9a of ring 2(66)
1123	30	26	–	–	C5-C14 str(19),mode 19a of ring 2(11),mode 19a of ring1(16)
1082	12	2	–	1097m	mode 18b of ring 1(69)
1072	6	0	–	–	mode15 of ring 2(78)
1039	6	1	–	1029m	H12- N11-C6 bend(44)
1016	3	6	–	1001s	mode 18a of ring 2(82)
979	2	10	–	–	mode 12 of ring 2(60)
965	0	0	–	–	mode 5of ring 2(81)
943	3	0	946 w	951w	mode 5 of ring 2(93)
926	46	1	–	925w	mode 17b of ring 1 (42),mode 17b of ring 2(15)
917	0	0	–	–	mode 17a of ring 1(82)
910	10	1	–	–	mode 10b of ring 2(56),mode 10b of ring 1(11)
884	12	1	889 w	888w	mode 10a of ring 1(78)
834	3	2	826s	833s	mode 10a of ring 2(87)
817	21	9	–	–	mode 10a of ring 1(36)
797	30	1	801  w	801w	mode 6 of ring 1(66)
786	10	1	762  w	766s	mode 10a of ring 1(20),mode 10a of ring 2(12), O26-C5-C15-C14 out(31)
743	36	7	–	743w	mode 10a of ring1(13)
723	18	1	–	–	mode 10a of ring 2(27)
686	30	1	700 w	–	mode 11 of ring 2(84)
671	5	0	660 w	666m	mode 6b of ring 1(32),mode 6b of ring 2(13),O26-C5-C15-C14 out(12)
648	37	3	644 w	648w	mode 6a of ring 1(11),mode 6a of ring 2(23)
636	20	1	–	618w	mode 6a of ring 1(43),C3-Cl10 str(10)
608	0	3	–	–	mode 6b of ring 2(83)
591	69	2	–	562m	H12-N11-C6-C1 tor(75)
546	8	5	–	–	mode 4 of ring 1(22),mode 4 of ring 2(11)
513	17	1	520 m	–	mode 16b of ring 1(62)
454	8	4	468 w	467m	N11-C6-C1  bend(60)
437	13	0	–	–	mode 16b of ring 1(49)
421	4	3	–	426m	mode 16b of ring1(33)
403	3	3	–	408sh	mode 16a of ring 2(86)
385	50	5	–	–	C2-C3-C4 bend(36)
371	123	7	–	378m	C3– Cl10str(17), H13-N11-C6-C5 tor(42)
358	53	8	–	–	C3-Cl10 str (26), H13-N11-C6-C5 tor(25)
312	4	1	–	323m	mode 16b of ring 1(60)
301	7	3	–	–	Cl10-C3-C4 bend(60)
255	0	3	–	265m	C5-C14 str(39)
218	1	10	–	227m	C4-C5-C14– C15 tor(12), C4-C3– Cl10(48)
175	1	9	–	190m	Cl10-C3-C4 bend(18),C14-C16-C20-C15 out(11),C4-C5-C14 bend(29)
129	3	9	–	149s	C14-C16-C20-C15 out(66)
115	1	6	–	111vs	C1-C2-C3-C4 tor(79)
73	0	36	–	82 s	C14-C16 -C20-C15 out(38),C4-C3-Cl10 bend(30)
54	0	100	–	–	C4-C5-C14-C15 tor(60),C4-C3-Cl10 bend(12)
39	1	34	–	–	C1-C2-C3-C4 tor(82)

vs-very strong; s-strong; m-medium; sh-shoulder; w-weak; vw-very weak; ring-phenyl ring; str-stretching; bend-bending; tor-torsion; sci-scissoring; wag-wagging; sym-symmetric; asy- asymmetric; out – out-of-plane bending

^COnly PED values greater than 10% are given.

Normal vibrations 8a, 8b, 19a, 19b and 14 are categorized as C-C stretching vibrations in phenyl ring ²⁴. The mode 8a of the mono-substituted ring vibrations usually appears in the region 1614-1575 cm^-1 and 8b mode extends around 1597-1562 cm^-1. The normal mode 8a is found at higher wavenumber than 8b and appears as a strong band in Raman at 1596 cm^-1 (PED 61%). The mode 8b of the mono-substituted ring Ph₂ is also observed in Raman as a weak shoulder band at 1575 cm^-1. The vibrational modes 19b, 19a and 14 of ring1 are computed at 1534, 1459 and 1398 cm^-1, respectively and the band at 1326 cm^-1 also has contribution from mode 14. The mode 19b is found to be a strong band at 1536 in IR and at 1537 cm^-1 in Raman while for 19a, a weak band at 1466 cm^-1 in IR and a strong band at 1464 cm^-1 are observed. Vibration 14 can be observed as a medium band in IR at 1405 cm^-1 and as a strong band in Raman at 1410 and a medium band at 1359 cm^-1. The simultaneous appearance of the ring C-C stretching bands in both IR and Raman modes of 19a, 19b and 14 evidence for the charge transfer interactions ^25,26.

The in-plane CH bending vibrations allowed by the asymmetrically tri-substituted phenyl rings are 3, 9b, 18b and 15 which are computed at 1295, 1148, 1082 and 1148 cm^-1, respectively which are in accordance with the previously reported vibrational assignments ²⁷. The wavenumbers of the above mentioned vibrational modes correlate with the experimental values except the mode at 1148 cm^-1. The mode 3 is found to be a medium band in Raman at 1296 cm^-1 and that in IR as a shoulder band at 1291 cm^-1. The mode 9b of ring1 is found to be strong in Raman at 1153 cm^-1 and that in IR as a medium band at 1150 cm^-1 (PED 56%) . The mode 18b of the ring1 is found only in Raman as a medium band at 1097 cm^-1. The normal modes 3, 9a, 5, 18a and 18b are classified as CH in-plane bending vibrations in mono-substituted benzene rings. The bands observed at 1291 cm^-1 in IR and that at 1296 cm^-1 in Raman are assigned to the mode 3 of Ph₂. The vibrational mode 9a is observed as a medium band in IR at 1150 cm^-1 and Raman at 1153 cm^-1 (PED 66%) as a strong band. The mode 18a occurs as a strong band in Raman at 1001 cm^-1 (PED 82%).

The C-H out-of-plane bending of phenyl ring 1 are computed at 925 and 743cm^-1 for 17b and 11 modes, respectively and the computed values correlate well with the experimental band positions showing that the C-H out-of-plane bending modes are less influenced by intermolecular interactions. The out-of-plane skeletal mode 6a of ring1 and 2 are found at 644 in IR and 648 cm^-1 in Raman as weak bands. The C-H out-of-plane bending (5,10a, 10b, 11,17a), radial skeletal (1,12, 6a and 6b) and the out-of-plane skeletal (4,16a and 16b) of Ph2 vibrations are also listed in table 4.

C=O vibrations

The benzophenone skeleton forms the tripod that has C=O bond as one branch and other two branches are formed from phenyl rings. Because of the different electro-negativities of carbon and oxygen atoms, the bonding electrons are not equally distributed between the two atoms. The lone pair of electrons on oxygen also determines the nature of the carbonyl group ²⁸. In the vibrational assignments of aromatic and aryl aliphatic ketones, Kolev ²⁹ observed the bands of ν(C=O) for 14 different aromatic and aryl aliphatic ketones. The C=O stretching vibrations give rise to the characteristic bands in IR and Raman and the intensity of these bands can increase owing to the conjugation or formation of hydrogen bonds. The C=O stretching of ketones are expected in the region 1760-1730 cm⁻¹. A strong intense and well defined peak observed in Raman at 1617 cm^-1 is due to the C=O stretching vibration of the carbonyl group. Similarly a highly intense band is observed at 1616 cm^-1 in IR also due to C=O stretching (PED 69%). The lowering of C=O stretching wavenumber is due to the conjugation between the carbonyl group and the aromatic ring and also due to the formation of hydrogen bonding.

Amino group vibrations

The amino group is generally referred to as an electron donating substituent in aromatic ring system. The asymmetric interaction between the amino group and the aromatic ring produce a small displacement of the N-atom out of the benzene ring.  In the region 3700-3300 cm^-1, only two bands are observed. The higher wavenumber band which is intense in the IR spectrum (3418 cm^-1) has been assigned to asymmetric stretching (PED100%) in amino group vibration. The intense band in IR spectrum (3314 cm^-1) and the medium band in Raman (3315 cm^-1) have been assigned to symmetric stretching (PED100%) of amino group vibrations. These assignments find support from the work of other researchers in the case of related molecules ³⁰. These wavenumbers and the ratio of intensities of the two bands are characteristic of NH₂ stretching mode. The lowering of NH stretching wavenumber is due to intermolecular N-H^…O interaction. The red-shifting of wavenumber in the NH bond order value is occurring due to donor-acceptor interactions.  The NH₂ stretching vibrations show the characteristic wavenumber shift caused by the halogen substituent also. Due to the low symmetry of the molecule, several internal coordinates also contribute to each normal mode. The NH scissoring deformation of amino groups appear around 1610-1630 cm⁻¹ and the rocking deformation around 1070-1050 cm^{-1 22}. The bands observed at 1617 and 1616 cm^-1 in Raman and IR were assigned to the scissoring modes of NH₂ group. The band identified at 1575 cm^-1 in Raman was assigned to the rocking mode.

CCl vibrations

The vibrations belonging to the bond between the ring and the halogen atoms are worth to discuss here, since mixing of vibrations are possible due to the lowering of the molecular symmetry and the presence of heavy atoms on the periphery of the molecule ³¹. The assignments of CCl stretching and deformation vibrations have been made by comparison with similar molecules, para-bromophenol ³² and the halogen-substituted benzene derivatives ³³ assigned vibrations of C-X group (X=Cl, Br and I) in the wavenumber range of 1129-480 cm^-1. Normally the CCl stretching bands are expected around 1060-395 cm^{-1 34}. In the 2A-5CB a weak Raman band at 618cm⁻¹ is assigned to CCl stretching vibration. A medium band at 227 cm⁻¹ (PED 48%) and a strong Raman band at 82 cm⁻¹ (PED 30%) are assigned to CCl bending vibrations, which are coupled with C-C-C vibrations.

Nonlinear optical property analysis

Polarizability characterizes the ability of an electric field to distort the electronic distribution of a molecule. Higher order polarizabilities (hyperpolarizabilities β,γ) which describe the nonlinear response of atoms and molecules are related to a wide range of phenomenon from nonlinear optics to intermolecular forces, such as the stability of chemical bonds as well as the conformation of molecules and molecular aggregates ³⁵. These studies led to the fact that ab initio calculations of polarizabilities and hyperpolarizabilities have become available through the strong theoretical basis for analyzing molecular interactions. They made possible for the determination of the elements of these tensors from derivatives of the dipole moment with respect to the electric field. Since polarizabilities and hyperpolarizabilities are derivatives of the molecular energy with respect to the strength of the applied electric field, their theoretically calculated values may be sensitive to basis-sets and the levels of theoretical approach employed and the electron correlation can change the values of hyperpolarizabilities ^36-40. Even order hyperpolarizabilities are zero, vanishing for systems with inversion symmetry. However, in the present case the situation differs since, 2A-5CB is a non-centrosymmetric molecule possessing a permanent dipole moment, where the polarization response to an external electric field of fixed strength dominated by the π-electrons found that the origin of the nonlinearity is to be sought not only in the independent bonds formed by the σ electrons which contribute linearly, but in the delocalized π electron cloud.

The static hyperpolarizability (b₀) and it’s related properties (b, a₀ and Da) have been calculated on the basis of the finite-field approach. In the presence of an applied electric field the first-order hyperpolarizability is a third rank tensor that can be described by a 3 x 3 x 3 matrix. The components of b are defined as the coefficients in the Taylor series expansion of the energy in the external electric field. When the external electric field is weak and homogeneous, the expansion becomes.

E = E⁰ – μαFα- 1/2aαβFαFβ- 1/6βα_βγFαFβFγ+…                                                      ————— (3)

where, E⁰ is the energy of the unperturbed molecules, Fα is the field at the origin μα _, α_αβ  and βαβγ are the components of dipole moment, polarizabilityand the first-order hyperpolarizability, respectively. From this, the first-order hyperpolarizability (β₀) using the x, y, z component is defined as

 

The calculated first-order hyperpolarizability of 2A-5CB is 1.53 x 10^-30 e.s.u.,which is 6 times greater than that of urea. From the computation, the high values of the hyperpolarizabilities of 2A-5CB are probably attributed to the charge transfer existing between the phenyl rings within the molecular skeleton. This is the evidence for nonlinear optical property of the molecule. The analysis of the wave function indicates that the electronic absorption corresponds to the transition from the ground to the first excited state and is mainly described by one-electron excitation from the highest occupied molecular orbital (HOMO) to the lowest unoccupied molecular orbital (LUMO). The atomic orbital compositions of the frontier molecular orbitals are sketched in Fig. 5. The HOMO energy=-8.19 eV, LUMO energy=-5.92 eV and HOMO-LUMO energy gap=2.2 eV. In addition, the decrease in HOMO and LUMO energy gap explains the eventual charge transfer interaction taking place within the molecule which is responsible for the NLO activity.

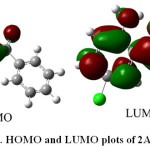Figure 5: HOMO and LUMO plots of 2A-5CB   Click here to View figure

 

Analysis of organic molecules having conjugated π-electron systems and large hyperpolarizability using IR and Raman has been evolved as a subject of recent research ⁴¹. The potential applications of 2A-5CB in the field of nonlinear optics demands the investigation of its structural and bonding features contributing to the hyperpolarizability enhancement by analyzing the vibrational modes using the IR and Raman spectra. The selection rule predicts the splitting of vibrational mode 19 (19a and 19b) in substituted phenyl rings. The modes 19a, 19b and 14 are active in both IR and in Raman simultaneously and their relative intensities are comparable which gives the evidence of the charge transfer from the donor to the acceptor group via the conjugated path, inducing charge variations in dipole moment and polarizability.

The C=O stretching vibrations give rise to the characteristic bands in the IR and Raman , and intensity of these bands can increase owing to the conjugation of formation of hydrogen bonds. The lowering of carbonyl stretching wavenumber is also contributed  by the  electron releasing effect of the C=O bond in the acceptor unit owing to intramolecular charge transfer as  reported earlier ⁴² in addition to the intermolecular effect and π-conjugation. Electron releasing effect  in the C=O double bond causes polarizability change  during vibration, making the Raman band  also strong whose intensity is comparable to that of IR band.

Conclusion

The red-shift of the NH stretching wavenumber in the infrared spectrum indicates the presence of N-H^…O bonding, resulting in proton transfer which increases the molecular hyperpolarizability of the material. The N-H^…O hydrogen bonding network and the intramolecular charge transfer interaction has been analyzed using NBO analysis. The π-electron delocalization over the carbazone moiety is responsible for the nonlinearity of the molecule. The simultaneous activation of the mode19 supports the charge transfer interaction. The calculated first-order hyperpolarizability of 2A-5CB is to be 1.53 x 10^-30 e.s.u.The enhancement of hyperpolarizability value and the lowering of HOMO-LUMO energy gap confirms charge transfer interaction arise in the molecule.

Acknowledgement

Prof. Michał H. Jamróz, Institute of Nuclear Chemistry and Technology, Warsaw, Poland for providing VEDA4 program.

References

1. Vul, E.B.; Lobanova, G.M. Kristallografiya. 1967, 12, 411-413.
2. Fleischer, E.B.; Sung, N.; Hawkinson, S. J. Phys. Chem. 1968, 72, 4311-4312.
   CrossRef
3. Babu, G.A; Thirupugalmani, K.; Jayaprakasan, M.; Ramasamy, P. J. Cryst. Growth. 2009, 311, 1607-1611.
   CrossRef
4. Babu, G.A.; Ramasamy, P. Mater. Chem. Phys. 2010, 119, 533-538.
   CrossRef
5. Genbo, S.; Shouwu, G.; Feng, P.; Youping, H.; Zhengdong, L. J. Phys. D: Appl. Phys. B. 1993, 26, 236-237.
   CrossRef
6. Rauhut, G.; Pulay, P. J. Phys. Chem. 1995, 99, 3093-3100.
   CrossRef
7. Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb, M. A.; Cheeseman, J. R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G. A.; Nakatsuji, H.; Caricato, M.; Li, X.; Hratchian, H. P.; Izmaylov, A. F.; Bloino, J.; Zheng, G.; Sonnenberg, J. L.; Hada, M.; Ehara, M.; Toyota, K.; Fukuda, R.; Hasegawa, J.; Ishida, M.; Nakajima, T.; Honda, Y.; Kitao, O.; Nakai, H.; Vreven, T.; Montgomery, J. A., Jr.; Peralta, J. E.; Ogliaro, F.; Bearpark, M.; Heyd, J. J.; Brothers, E.; Kudin, K. N.; Staroverov, V. N.; Kobayashi, R.; Normand, J.; Raghavachari, K.; Rendell, A.; Burant, J. C.; Iyengar, S. S.; Tomasi, J.; Cossi, M.; Rega, N.; Millam, J. M.; Klene, M.; Knox, J. E.; Cross, J. B.; Bakken, V.; Adamo, C.; Jaramillo, J.; Gomperts, R.; Stratmann, R. E.; Yazyev, O.; Austin, A. J.; Cammi, R.; Pomelli, C.; Ochterski, J. W.; Martin, R. L.; Morokuma, K.; Zakrzewski, V. G.; Voth, G. A.; Salvador, P.; Dannenberg, J. J.; Dapprich, S.; Daniels, A. D.; Farkas, Ö.; Foresman, J. B.; Ortiz, J. V.; Cioslowski, J.; Fox, D. J. Gaussian, Inc., Wallingford CT, 2009.
8. Becke, A.D. J. Chem. Phys. 1993, 98, 5648.
   CrossRef
9. Lee, C.; Yang, W.; Parr, R.G. Phys. Rev. B. 1998, 37, 785-789.
   CrossRef
10. Keresztury, G.; Chalmers, J.M.; Griffith, P.R. (Eds.), Raman Spectroscopy: Theory, in: Hand Book of Vibrational Spectroscopy, John Wiley and Sons Ltd., New York, 2002.
11. Keresztury, G.; Holly, S.; Varga, J.; Besenyei, G.; Wang, A.Y.; Durig, J.R. Spectrochim. Acta A 1993, 49, 2007-2026.
    CrossRef
12. Hoffmann, R.; Swenson, J.R.; J. Phys. Chem. 1970, 74, 415-420.
    CrossRef
13. Akalin, E.; Akyüz, S. J. Mol. Struct. 1999, 482, 175-181.
    CrossRef
14. Reed, A.E.; Curtiss, L.A.; Weinhold, F. Chem. Rev. 1988, 88, 899-926.
    CrossRef
15. Foster, J.P.; Weinhold, F. J. Am. Chem. Soc. 1980, 102, 7211-7218.
    CrossRef
16. Weinhold, F.; Landis, C.R. Valency and Bonding: A Natural Bond Orbital Donor-Acceptor Perspective, Cambridge University Press, New York, 2005.
    CrossRef
17. Thompson, H.W.; Torkington, P. J. Chem. Soc. 1945, 640-645.
    CrossRef
18. Glendening, E.D.; Badenhoop, J.K.; Reed, A.E.; Carpenter, J.E.; Bohmann, J.A.; Morales, C.M.; Weinhold, F. NBO 3.1, Theoretical Chemistry Institute, University of Wisconsin, Madison, 2001.
19. Jamróz, M.H., Vibrational Energy Distribution Analysis VEDA4, Warsaw, 2004.
20. Wilson, E.B. Phys. Rev. 1934, 45, 706-714.
    CrossRef
21. Wilson, E.B.; Decius, J.C.; Cross, P.C. Molecular Vibrations: The Theory of Infrared and Raman Vibrational Spectra, Dover Publications, Inc., New York, 1955.
22. Varsanyi, G., Vibrational spectra of benzene derivatives, Academic Press, New York, 1969.
23. Ravikumar, C.; Hubert Joe, I.; Sajan, D. Chem. Phys. 2010, 369, 1-7.
    CrossRef
24. Anjaneyulu, A.; Ramana Rao, G. Spectrochim. Acta A. 1999, 55, 749-760.
    CrossRef
25. Ravikumar, C.; Hubert Joe, I.; Jayakumar, V.S. Chem. Phys. Lett. 2008, 460, 552-558.
    CrossRef
26. Ravikumar, C.; Hubert Joe, I.Phys. Chem. Chem. Phys. 2010, 12, 9452-9460.
    CrossRef
27. Green, J.H.S.; Harrison, D.J. Spectrochim. Acta A 1976, 32, 1265-1277.
    CrossRef
28. Sathyanarayan, D.N., Vibrational spectroscopy-theory and applications, New age International (P) Ltd., New Delhi, 2004.
29. Kolev, T. J. Mol. Struct., 1995, 349, 381-384.
    CrossRef
30. Rostkowska, H.; Nowak, M.J.; Lapinski, L.; Bretner, M.; Kulikowski, T.; Leimage, A.; Adamowicz, L. Spectrochim. Acta A, 1993, 49, 551-565.
    CrossRef
31. Yadav, R.A.; Sing, I.S. Indian J. Pure Appl. Phys. 1985, 23, 626-631.
32. Zierkiewicz, W.; Michalska, D.; Huyskens, T.Z.  J. Phys. Chem. A, 2000, 104, 11685-11692.
    CrossRef
33. Varsanyi, G., Assignments for vibrational spectra of seven hundred benzene derivatives, Adam Hilger, Mooney, 1974.
34. Colthup, N.B.; Daly, L.H.; Wiberley, S.E., Introduction to Infrared and Raman Spectroscopy, Academic Press, London, 1964.
35. Stephens, P.J.; Jalkanen, K.J. J. Chem. Phys. 1989, 91, 1379-1382.
    CrossRef
36. Calaminici, P.; Jug, K.; Köster, A.M. J. Chem. Phys. 1998, 109, 7756-7759.
    CrossRef
37. Colwell, S.M.; Murray, C.W.; Handy, N.C.; Amos, R.D. Chem. Phys. Lett. 1993, 210, 261-268.
    CrossRef
38. McDowell, S.A.C.; Amos, R.D.; Handy, N.C. Chem. Phys. Lett. 1995, 235, 1-4.
    CrossRef
39. Hermann, J. P.; Ricard, D.; Ducuing, J. Appl. Phys. Lett. 1973, 23, 178-181.
    CrossRef
40. Tommasini, M.; Castiglioni, C.; Del Zoppo, M.; Zerbi, G. J. Mol. Struct. 1999, 480, 179-188.
    CrossRef
41. Nakano, M.; Shigemoto, I.; Yamada, S.; Yamaguchi, K. J. Chem. Phys. 1995, 103, 4175-4181.
    CrossRef
42. Delgado, M.C.R; Hernández, V.; Casado, J.; Navarrete, J.T.L.; Raimundo, J.-M.; Blanchard, P.; Roncali, J. J. Mol. Struct., 2003, 651, 151-158.
    CrossRef

---

This work is licensed under a Creative Commons Attribution 4.0 International License.