Comparative Study of Molecular Interactions in Binary Liquid Mixtures of 4 –Methyl-2-pentanoneWith Butan-2-One, Furfuraldehyde, Cyclohexanone At 308 K

Introduction

The dielectric [1] and ultrasonic studies [2-4] have beenprovided many data in precisely understanding the molecular interactions and the structural behavior of molecules and their mixtures. During the last two decades, ultrasonic study of liquid mixtures due to its non-destructive nature wascarried out in different branches of science to measure the different properties to predict the nature of molecular interactions. The formation of molecular clusters and network structures due to strong intermolecular interactions through H-bonds in alcohols results in their complicated molecular structures in liquid state. The complexities in the H-bonded alcohol structures at the molecular level changes significantly in ternary mixtures of various characteristics of H-bonded liquids due to the breaking of their homogeneous structure and simultaneously the formation of H-bonded heterogeneous structures. The conformations of binary of industrial and biologically useful H-bonded liquids, particularly Ketenes, are the challenging problems in liquid state physics and chemistry. In the present work, ultrasonic velocity measurements on the ternary mixtures of 1- alkanets were carried out, in order to get ideas about some of the universal rules in the structural variation and formation of the H-bonded structure over the entire concentration variation of the mixture constituents.

Experimental Details 

Experimental techniques

Aspects in Theoretical

Adiabatic compressibility (β)

The adiabatic compressibility is the fractional decrease of volume per unit increase of pressure, when no heat flows in or out. These changes are related to the compressibility of the medium by thermodynamic relation.

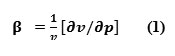
It can also be calculated from the speed of sound (U) and the density of the medium (ρ) using the equation of Newton Laplace as

 

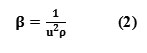
Intermolecular free length

The adiabatic compressibility of a liquid can be expressed in terms of the intermolecular free length which is the distance between the surfaces of the neighboring molecules and is given by the relation,

 

Where K_T is the temperature dependent constant.

Free Volume (V_f)

Free volume is one of the significant factors in explaining the variations in the physic-chemical properties of liquids and liquid mixtures. The free space and its dependent properties have close connection with molecular structure and it may show interesting features about interactions, which may occur when two or more liquids are mixed together. This molecular interactions between like and unlike molecules are influenced by structural arrangements along with shape and size of the molecules. A liquid may be treated as if it were composed of individual molecules each moving in a volume V_f in an average potential due to its neighbors. That is, the molecules of a liquid are not quite closely packed and there are some free spaces between the molecules for movement and the volume V_f is called the free volume [24].Eyring and Kincaid [25] defined the free volume as the effective volume in which particular molecule of the liquid can move and obey perfect gas laws Free volume in terms of Ultrasonic velocity (U) and the Viscosity of the liquid (η) as

 

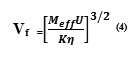
Where M_eff  is the effective molecular weight

 

in which m_i and X_i are the molecular weight and the mole fraction of the individual constituents respectively). K is a temperature independent, constant which is equal to 4.28×10⁹ for all liquids.

Internal Pressure (π_i)

The measurement of internal pressure is important in the study of the thermodynamic properties of liquids. The internal pressure is the cohesive force, which is a resultant of force of attraction and force of repulsion between the molecules [26].Cohesion creates a pressure within the liquid of value between 103 and 104  atmosphere. Internal pressure also gives an idea of the solubility characteristics. Dissolved solutes exist under the internal pressure of the medium and their interactions with the solvent arise through hydrogen bonding, charge transfer, Columbic (or) Vanderwaal’s interaction. The term a/v² in Vanderwaal’s [27] equation being the measure of attractive force of the molecule is called the cohesive (or) internal pressure.

The internal pressure is the single factor which varies due to all type of solvent-solute, solute-solute and solvent-solvent interactions. A general method of measuring the internal pressure based on the Maxwell’s equation of thermodynamics [5] is

 

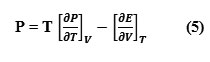
On the basis of statistical thermodynamics, expression for the determination of internal pressure by the use of free volume concept as given by

 

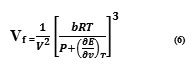
As (ςE/av)is the internal pressure and neglecting P which is insignificantly  small  to π_i

 

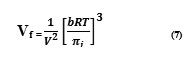
The final equation for the evaluation of internal pressure can be obtained by combining and rearranging the equations (6) and (7)

 

Where K is a constant, T the absolute temperature, η , the viscosity in NSm-2, U, the

ultrasonic velocity in ms-1, ρ, the density in kgm-3 of the liquid.

Relaxation time (τ)

Relaxation time is the time taken for the excitation energy to appear as translational energy

and it depends on temperature and on impurities.

The dispersion of the ultrasonic velocity in binary mixture reveals information about the characteristic time of the relaxation process that causes dispersion. The relaxation time (τ) can be calculated from the relation.

 

Acoustic Impedance (Z)

The Specific acoustic impedance is given by

Z =Uρ                             (10)

Where U and ρ are velocity and density of liquid respectively.

Gibb’s Free Energy (ΔG*)

The relaxation time for a given transition is related to the activation free energy. The Variation of KTwith temperature can be expressed in the form of Eyring salt process theory.

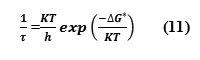
The above equation can be rearranged as,

 

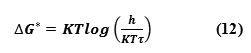
Where K is the Boltzmann constant and h is plank’s constant. The excess values are calculated using the formula,

Where, Aid = ΣAiXi, where Ai is any acoustical parameter and Xi is the mole fraction of liquid component.

Experimental

Density Measurement

The density of pure liquids and mixtures are measured using a 10ml specific gravity bottle.

The specific gravity bottle with the experimental liquid is immersed in a temperature

Controlled water bath. The densities of pure liquids thus obtained are found to be in good

Agreement with standard values. The measured density was measured using the formula,

 

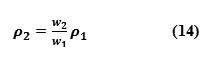
Where,

W₁ is the weight of the distilled water.

W₂, is the weight of the experimental liquid

p1 is the density of water.

p2 is  the density of experimental liquid.

Viscosity measurement

The viscosity of the pure liquids and liquid mixtures are measured using an Ostwald’s Viscometer

calibrated with doubly distilled water. The Ostwald’s Viscometer with the experimental liquid is

immersed in a temperature controlled water bath. The time of flow was measured using a Racer stopwatch with an accuracy of 0.1 sec. Viscosity was determined using the relation

 

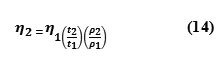
Where,

n₂ is the Viscosity of water

t₁ , is the time of flow of water

p₁  is the density of water.

n₁ is the viscosity of the experimental liquid.

t₂ is the time of flow of the experimental liquid.

p₂ is the density of the experimental liquid.

Velocity Measurement

The velocity of ultrasonic waves in the liquid mixture have been measured using an ultrasonic interferometer (Mittal Enterprises, New Delhi) working at a fixed frequency of 2MHZ with a tolerance of ± 0.005%. The measuring cell is a specially designed double walled vessel with provision for temperature constancy. The high frequency generator excites a quartz crystal fixed at the bottom of the measuring cell, at its resonant frequency. The capacity of the measuring cell is 12cc. A fine micrometer screw, with a least count of 0.01mmat the top of the cell, can be raised (or) lowered the reflector plate in the liquid through a known distance. The measuring cell is connected to the output terminals of the high frequency generator through a shielded cable. Ultrasonic  waves, normal to quartz crystal, is reflected from the reflector plate. Stationary waves are formed in the region between reflector plate and the quartz crystal. The micrometer is slowly moved till a number of maximum readings (n) of the anode current is passed. The total distance moved by the micrometer is noted (d).The wavelength of the ultrasonic waves in the liquid is λ =2d/n. The velocity of ultrasonic waves in the liquid U = λf .Where f is the frequency of the generator.

System:-1   4 –Methyl-2-Pentanone + Butan-2-One

 Table 1: Mole fraction of first component (X₁),    Mole fraction of second component(X₂), Density(ρ), viscosity(η), ultrasonic  velocity(U), acoustic impedance(Z), Leonard’s Jones potential(LJP) and Molecular interaction parameter(χ_u)values at different mole fraction of  IBMK + butan-2-one at 308 K.

MOLE FRACTION		ρ (Kg/m3)	η *10-5(NpM-2)	U(m/s)	Z*10-3 (Kgm-2s-1)	LJP	χu*10-3 (m/s)
X1	X2
0	1	977.5	5.27	1414	13.82	6	23.17
0.0829	0.9171	959.7	4.48	1363	13.08	6	19.07
0.1506	0.8494	946.8	4.35	1334	12.63	6	16.81
0.2371	0.7629	930.4	4.14	1305	12.14	6	14.62
0.3871	0.6129	902.5	3.94	1268	11.44	6	11.96
0.4641	0.5359	888.2	3.52	1246	11.07	6	10.32
0.6312	0.3688	867.4	3.17	1224	10.62	6	9.01
0.6448	0.3552	856.7	2.81	1220	10.45	6	8.71
0.7789	0.2211	832.6	2.59	1202	10.01	6	7.62
0.8846	0.1154	813.2	2.20	1191	9.69	6	7.04
1.0000	0.0000	977	5.2	1324	8.86	6	6.54

 

βs*10-3 (T.Pa)-1	τ10-4 (s)	Vf (ml/mole)	πi (atm)	CE*10-2 (KJ/mole)	α/f2103 (NPm-1s2)	Lf*10-3 A0	ΔG#10-20(KJ/mole)
5.12	7.18	4.6321	747.46	41.47	0.3718	0.115	0.005
5.61	6.23	7.39193	672.27	39.24	0.3617	0.117	0.005
5.94	6.12	8.20345	646.57	37.89	0.3554	0.119	0.005
6.31	5.94	9.73763	611.44	36.43	0.3484	0.121	0.005
6.89	5.82	12.1499	562.63	34.33	0.3383	0.124	0.005
7.25	5.29	17.4198	517.53	33.20	0.3327	0.126	0.0050.005
7.70	4.87	26.5732	462.24	31.85	0.3258	0.130
7.84	4.37	38.3794	430.28	31.36	0.3233	0.130	0.0050.005
8.31	4.14	53.1831	391.74	30.02	0.3164	0.133
8.67	3.61	92.127	346.46	29.06	0.3112	0.136	0.0050.005
8.69	6.63	18.2302	439.19	28.66	0.3091	0.138

 

SYSTEM:-1     4 –Methyl-2-Pentanone +BUTAN-2-ONE

Table 2: Adiabatic compressibility(β), relaxation time(τ), free volume(V_f), internal pressure(π_i), cohesive force(CE), absorption co-efficient(α/f²), free length(L_f)& activation energy(ΔG^#)  values at different mole fraction of chlorobenzene+ IBMKat  308K.

βs*10-3 (T.Pa)-1	τ10-4 (s)	Vf (ml/mole)	πi (atm)	CE*10-2 (KJ/mole)	α/f2103 (NPm-1s2)	Lf*10-3 A0	ΔG#10-20 (KJ/mole)
5.12	7.18	4.6321	747.46	41.47	0.3718	0.115	0.005
5.61	6.23	7.39193	672.27	39.24	0.3617	0.117	0.005
5.94	6.12	8.20345	646.57	37.89	0.3554	0.119	0.005
6.31	5.94	9.73763	611.44	36.43	0.3484	0.121	0.005
6.89	5.82	12.1499	562.63	34.33	0.3383	0.124	0.005
7.25	5.29	17.4198	517.53	33.20	0.3327	0.126	0.005

System:-2    4 –Methyl-2-Pentanone +Cyclohexanone

 Table 1:  Mole fraction of first component (X₁),    Mole fraction of second component(X₂), Density(ρ), viscosity(η), ultrasonic  velocity(U), acoustic impedance(Z), Leonard’s Jones potential(LJP) and Molecular interaction parameter(χ_u)values at different mole fraction of  IBMK + Aniline at 308 K.

 

MOLE FRACTION		ρ (Kg/m3)	η *10-5(NpM-2)	U(m/s)	Z*10-3 (Kgm-2s-1)	LJP	χu*10-3 (m/s)
X1	X2
0.0000	1.0000	939	9.62	1366.00	12.83	41	-3.87
0.0727	0.9273	929.4	9.04	1402.00	13.03	48	-0.23
0.1115	0.8885	922.6	8.34	1378.00	12.71	43	-1.35
0.1713	0.8287	912.6	7.70	1356.00	12.37	39	-2.01
0.2916	0.7084	894.4	6.78	1327.00	11.87	35	-2.26
0.3583	0.6417	884.6	6.15	1304.00	11.54	32	-2.92
0.4853	0.5147	865.8	5.46	1289.00	11.16	31	-2.03
0.5485	0.4515	856.4	4.84	1267.00	10.85	29	-2.69
0.6949	0.3051	835.9	4.30	1249.00	10.44	27	-1.67
0.8435	0.1565	815.6	3.63	1224.00	9.98	26	-1.13
0.9179	0.0821	800.6	3.21	1220.00	9.77	25	-0.15
1.0000	0.0000	939	9.62	1204.00	12.83	24	-3.87

SYSTEM:-2  4 –Methyl-2-pentanone +CYCLOHEXANONE

Table 2: Adiabatic Compressibility(Β), Relaxation Time(Τ), Free Volume(V_f), Internal Pressure(Π_i), Cohessive Force(CE), Absorption Co-Efficient(Α/F²), Free Length(L_f)& Activation Energy(ΔG^#)  Values At Different Mole Fraction Of IBMK + Aniline  At  308 K.

βs*10-3 (T.Pa)-1	τ10-4 (s)	Vf (ml/mole)	πi (atm)	CE*10-2 (KJ/mole)	α/f2103 (NPm-1s2)	Lf*10-3 A0	ΔG#10-20(KJ/mole)
0.57	73.23	0.1857	399.46	4.18	0.017	0.120	0.003
0.55	65.97	0.2126	378.87	4.01	0.014	0.119	0.003
0.57	63.50	0.2339	365.06	3.89	0.012	0.120	0.003
0.60	61.15	0.2582	350.37	3.78	0.011	0.122	0.003
0.63	57.40	0.3034	327.07	3.61	0.009	0.124	0.003
0.66	54.48	0.3431	311.35	3.48	0.008	0.126	0.003
0.70	50.60	0.4044	290.07	3.32	0.007	0.128	0.003
0.73	46.93	0.4731	273.05	3.16	0.006	0.130	0.003
0.77	43.95	0.5556	254.16	3.03	0.005	0.132	0.003
0.82	39.60	0.6979	231.27	2.83	0.003	0.135	0.003
0.84	35.92	0.8366	214.82	2.68	0.003	0.137	0.003
0.57	73.23	0.6026	399.46	4.18	0.017	0.120	0.003

 

SYSTEM:-3  4 –Methyl-2-pentanone +FURFURALDEHYDE

 Table 1:  Mole fraction of firstcomponent (X₁),    Mole fraction of second component(X₂), Density(ρ), viscosity(η), ultrasonic  velocity(U), acoustic impedance(Z), Leonard’s Jones potential(LJP) and Molecular interaction parameter(χ_u)values at different mole fraction of  IBMK + N,N-Dimethyl Aniline at 308 K.

MOLE FRACTION		ρ (Kg/m3)	η *10-5(NpM-2)	U(m/s)	Z*10-3 (Kgm-2s-1)	LJP	χu*10-3 (m/s)
X1	X2
0	1	1147.7	8.25	1372	1574.6444	42.1053	0
0.0581	0.9419	1119	7.19	1380	1544.22	43.6364	0.0130
0.094	0.906	1101.7	6.59	1368	1507.1256	41.3793	0.0087
0.1442	0.8558	1078.2	6.09	1376	1483.6032	42.8571	0.0209
0.2533	0.7467	1030.2	5.30	1379	1420.6458	43.4389	0.0373
0.3077	0.6923	1008	4.92	1330	1340.64	35.5556	0.0073
0.4325	0.5675	962.3	4.37	1272	1224.0456	29.2683	-0.0210
0.4941	0.5059	938.5	3.93	1256	1178.756	27.9070	-0.0256
0.6501	0.3499	888	3.47	1228	1090.464	25.8065	-0.0275
0.8028	0.1972	844.1	2.99	1216	1026.4256	25	-0.0171
1	0	793.7	3.95	1204	955.6148	24.2424	0

 

βs10 -12 (T.Pa)-1	τ10-5 (s)	Vf (ml/mole)	πi (atm)	CE (gJ/mole)	α/f210 3 (NPm-1s2)	Lf (T.Pa)-1	ΔG#10 -20 (Gj/mole)
46.2875	0	0.1438	3785	487	21.5812	118	2.90369
46.9258	-204.66	0.1625	3645	467	18.6268	119	2.88907
48.5025	-211.53	0.1888	3471	444	15.5316	120	2.87196
48.9851	-189.07	0.2163	3321	424	13.1346	121	2.85616
51.0446	-164.03	0.2447	3193	407	11.5736	124	2.84382
56.0836	-166.69	0.2805	3054	389	9.6677	124	2.82689
64.2267	-160.18	0.3155	2942	373	8.8179	128	2.81786
67.5439	-169.98	0.3342	2888	366	8.4674	130	2.8138
74.6776	-162.6	0.3731	2830	350	7.6573	131	2.79929
80..119	-164.11	0.4181	2727	337	6.7979	134	2.78794
86.9142	0	0.5096	2535	316	5.3504	136	2.76818

 

SYSTEM:-3  4 –Methyl-2-pentanone +FURFURALDEHYDE

Table:-2    Adiabatic Compressibility(Β), Relaxation Time(Τ), Free Volume(V_f), Internal Pressure(Π_i), Cohesive Force(CE), Absorption Co-Efficient(Α/F²), Free Length(L_f)& Activation Energy(ΔG^#)  Values At Different Mole Fraction Of IBMK + N,N-Dimethyl Aniline At  308 K.

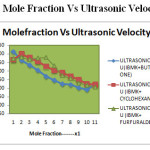Figure 1: Mole Fraction Vs Ultrasonic Velocity  Click here to View figure

 

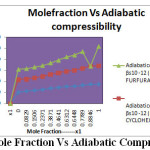Figure 2: Mole Fraction Vs Adiabatic Compressibiliy  Click here to View figure

 

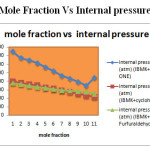Figure 3: Mole Fraction Vs Internal pressure   Click here to View figure

 

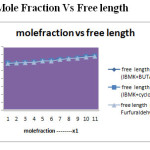Figure 4: Mole Fraction Vs Free length   Click here to View figure

 

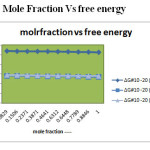Figure 5: Mole Fraction Vs free energy   Click here to View figure

 

Results and Discussion

From the tables 1 ,4 &7,it is noted that the density decreases with increase in mole fraction for 4–Methyl-2-pentanone+buyan-2-one, 4–Methyl-2-pentanone+cyclohexanone and 4–Methyl-2-pentanone+furfuraldehyde. Ultrasonic velocity and viscosity decreases with increase in mole fraction of the solute in 4–Methyl-2-pentanone+buyan-2-one, 4–Methyl-2-pentanone+cyclohexanone and 4–Methyl-2-pentanone+furfuraldehyde.

From the tables 1 ,3&5. The corresponding plots are given in Figs-2and 4.it is noted that the decrease in velocity is due to the increase in free length and adiabatic compressibility.The decrease in velocity is due to the increase in free length and adiabatic compressibility of the liquid mixtures  system 4–Methyl-2-pentanone+buyan-2-one, 4–Methyl-2-pentanone+cyclohexanone and 4–Methyl-2-pentanone+furfuraldehyde.. It is observed that for a given concentration as the number of CH group or chain length increases, the sound velocity increases.

From the tables 2,4 and 6, The corresponding plots are given in Figs- 2 and 4. It is noted that the adiabatic compressibility and free length increases with increase of mole fraction in system 4–Methyl-2-pentanone+cyclohexanone and 4–Methyl-2-pentanone+furfuraldehyde.  This may lead to the presence of specific molecular interaction between the molecules of the liquid mixture. The adiabatic compressibility and free length are the deciding factors of the ultrasonic velocity in liquid systems. The internal pressure decreases and free volume increases with increasing mole fraction.

The internal pressure free volume values are tabulated in 2,4 and 6.The corresponding plots are given in Figs-3 and4.  it is noted that the internal pressure may give information regarding the nature and strength of forces existing between the molecules. The decrease in free volume shows that the strength of interaction decreases gradually with the increase in solute concentration. It represents that   there is weak interaction between the solute and solvent molecules.

When two liquids are mixed, there is a molecular attraction between the molecules of components and hence the cohesive energy is high. The cohesive energy and absorption coefficient  values are decreased  with increases  in mole fractions  in all the systems which may be due to weak induced dipole-induced dipole interactions in all systems..

From the tables 1,3 and 5.Acoustic impedance decreases with increase of mole fraction in all the three systems. The relaxation time (τ) decreases with increasing concentration for all the three systems.

The dispersion of the ultrasonic velocity in the system should contain information about the characteristic time τ of the relaxation process that causes dispersion.

The relaxation time which is in the order of 10^-12 sec is due to structural relaxation process [28] and in such a situation it is suggested that the molecules get rearranged due to co-operative process[29].

The Gibb’s Free energy more or less same  with increasing mole fraction for  all the systems.

From the table1,3&7. The corresponding plots are given in Figs- 3, 13, 23.It is seen that the molecular interaction parameters values are more negative in system 4–Methyl-2-pentanone+cyclohexanone and 4–Methyl-2-pentanone+furfuraldehyde than 4–Methyl-2-pentanone+butan-2-one. It is suggested that dipole-dipole interactions stronger than induced dipole-induced dipole interactions.

From the table2,5&8. The corresponding plots are given in Figs- 6, 16,26. The Gibb’s Free energy decreases with increasing mole fraction of all the systems. This may be due to the intermediate compound formation between binary liquids. It is observed generally free energy decrease favors the formation of products from reaction. This Observation confirms the formation of hydrogen bonding in binary mixtures.

Hence from these factors, there is  less intermolecular hydrogen bond formation and less dipole-dipole interaction in 4–Methyl-2-pentanone+cyclohexanone and 4–Methyl-2-pentanone+furfuraldehyde than 4–Methyl-2-pentanone+butan-2-one.

Acknowlodgement

The author thanks to Dr. kesavaswamy,Dr.muthu vijayan Enoch and also  Dr.Ranghanath, principal of Adhiyamann College of engineering, Hosur-635 109, India.

Conclusion

The computed acoustical parameters and their values point to the presence of specific molecular interaction in the liquid mixtures 4–Methyl-2-pentanone+cyclohexanone and 4–Methyl-2-pentanone+furfuraldehyde than 4–Methyl-2-pentanone+butan-2-one. at 308 K. Hence it is concluded that the association in these mixtures is the result of strong Hydrogen bonding between the molecules & strong Dipole-Dipole interactions 4–Methyl-2-pentanone+cyclohexanone and 4–Methyl-2-pentanone+furfuraldehyde than 4–Methyl-2-pentanone+butan-2-one.  in Binary liquid mixtures.

The proportional studies of divergence in these systems are given by cumulative order. 4–Methyl-2-pentanone+cyclohexanone and 4–Methyl-2-pentanone+furfuraldehyde than 4–Methyl-2-pentanone+butan-2-one. These parameters will be useful in pharma and perfumes industries for handling &mixing process.

Reference

1. Tabhane V A and Patki B A, Acostica, 1982, 52, 44.
2. Tabhane V A, Acoustic letters, 1988, 6, 8.
3. Marvin B L and Bhat S N, Acostica1987, 64, 155.
4. Johari G K and Misra R C Indian J Pure &ApplPhys, 1987, 29,155.
5. Nikam P S and Hirey, Indian J Pure &ApplPhys, 1991, 29,155.
6. Gruenberg L and Nissan, Nature 1946,164, 799.
   CrossRef
7. Manohar Murthi N and Nagbhushnam, Indian J chem., 1984, 23, 510.
8. Khasare S B, Indian J Pure &ApplPhys, 1987, 25, 182.
9. Jacobson B, Acta chem., 1985, 6, 148.
10. Bhatti S S and Singh D P, Indian J Pure &ApplPhys1983, 21, 506.
11. Sheshadri A T and subramanyam B, J Physconds matter, 1990, 2, 7353.
12. Manohar Murthi N, Shivkumar K V, Rajgopal E and subramanyam S V, Acostica1981, 48 , 341.
13. Miyanga Stamura K and Murakami S, Jchem.Thermodynamics,1992,48,1767.
14. P Vigourex, Ultrasonics, Chapman and hall, London, 1952.
15. Rajgopal K and Chenthilnath, Indian J Pure &ApplPhys, 2010, 48, 326.
16. Hirschfelder J O, Kurtiss C F and Bird R B ,Molecular theory of gases and Liquids (John Willy, New York-01, 1954,256).
17. Sumathi T and Uma Maheswari, Indian J Pure &ApplPhys, 2009, 47, 782.
18. Rajedren V, Indian J Pure &ApplPhys1996, 34, 52.
19. Shanti N, Subrathinam P L and Emayavayramban M, 2010, 7, 648.
20. Bhatti S S, Vivek J S and Singh D P, Acoustica, 1982, 50, 291.
21. Palaniappan L and Thiyagarajan R, Indian J chem., 2008, 47B, 1906.
22. Hyderkhan, V.andSubramanyam, S.V., Tras. Parad Soc. (GB) 67,2282, (1971).
23. Temperley, H.N.V., Rawlinson, J.S. and Rush brooke, G.S., Phys. of simple liquids(John wiley,Newyork), (1968).
24. Glasstone, S., Laidler, K.J., and Erying, H., Theory of Rate Processes.
25. Mc. Graw – Hill, Newyork, 478, 479, (1950). Erying, H.and Kincaid, J.F.J.Chem.Phy.,6,520,(1938).
26. Richards, T.W., Chem. Rev., 2,315, (1925).
    CrossRef
27. Vanderwaals, J.d., Essay on the continuity of the gaseous and liquid States London (1873).
28. Glasstone, S., Thermodynamic for chemist, D. van Mostrand Co., Inc., Newyork, 62, (1947).
29. Ali, A., Hyder, S. and Nain, A.K., Ind.J. Phys. 74 B, 63 (2000).

---

This work is licensed under a Creative Commons Attribution 4.0 International License.