Ab initio and DFT Studies of Be(BH₄)₂

Introduction

Metal borohydrides are fascinating compounds because they show a remarkable variety in bonding characteristics ranging from ionic salts of alkali metals (e.g., LiBH₄ and NaBH₄) to volatile covalent compounds; in these compounds, hydrogen bridge bonds link boron to the metal. Among the covalent compounds, Al(BH₄)₃ is believed to have a planar trigonal skeletal structure with double hydrogen bridges [1, 2], while Zr(BH₄)₄, U(BH₄)₄ are all thought to have tetrahedral Td structures with triple bridges [3]. The borohydrides are among the most volatile compounds of the latter heavy metals; this characteristic is often used in their commercial purification.

They are observed in many shapes according to the bonding between borohydride groups with the central atom occurred as in Figure 1. To understand the bonding between the metal and the borohydride group BH₄, calculations of Molecular orbital (MO) are conducted to quantify that quantitative in formations including the interference energy and the exchange mechanism between bridge and terminal hydrogen atoms. This is very important for better understanding of bonding in those compounds [4]. To obtain these informations from the calculations of molecular orbital, Beryllium borohydride Be(BH₄)₂ was used as a typical compound to study similar transition elements compounds. This compound contains M-BH₄ bond which is not efficient as in the case of NaBH₄ and LiBH₄ [5], while the vibrational spectra is the best way used for obtaining an important information that may determine the optimized geometries for many compounds of Tetrahydroborate Ion [6, 7].

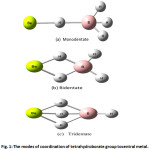Figure 1: The modes of coordination of tetrahydroborate group tocentral metal. Click here to View figure

 

In some cases, it was found that the vibrational spectra of the double bond or triple bond are very different in wide area of B-H, and this group can be determined in addition to the vibrational spectra. The determination of the kind of hydrogen bridge in these compounds essentially depends on the use of an experimental method such as X-ray diffraction and electron diffraction. Although it is easy to distinguish the hydrogen bonds in tetra borohydride group (double or triple bonds) in many compounds by X-ray diffraction, the determination is sometimes difficult in the presence of metals. This is because of the scattering force of hydrogen atoms to the x-ray and the electrons [7]. Several experiments were performed on Beryllium borohydride to conduce its composition in gas phase without any convenient results thus the molecular structure of Beryllium borohydride is one of the problems utnil now [8-11].

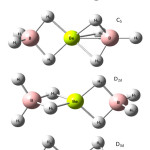Figure 2: Various possible structures of Be(BH4)2. Click here to View figure

 

Computational details

The optimized geometries, energy and vibrational frequency of the fundamental modes for the Beryllium borohydride Be(BH₄)₂ were computed of four different structures of Be(BH₄)₂ as in Figure 2. Three methods were used to approximate the energy and its Hartre – Fock (HF), Moller-plesset perturbation theory (MP2) and Becke- style 3 Parameter Density functional theory (B3LYP) with 6-31G(d), 6-311G(d,p), 6-311+G(d,p) and 6-311++G(d,p) basis sets using GAUSSIAN 03W program package [12].

Results and Discussion

Potential Energy Calculations

The relative energies (kcal/mol) have been calculated for each of the four structures of Beryllium borohydride by using the three methods, for the basis sets 6-31G(d), 6-311G(d,p), 6-311+G(d,p) and 6-311++G(d,p).Table 1 outlines the values of energy at these levels. In general, the structure of D_2d kind is more stable. The results of the relative values of energy assure that the structure D_2d is the most stable, while the the structure D_3d is less stable. This is consistent with the experimental result that was reached in a previous study [13]. It is clear that the difference in energy between the structures D_3d, C_s, C_3v at all levels is very small. This means that both C_s, C_3v are in agreement with the structure D_3d.

These results substantiated the values of bond lengths for both C_3v, C_s which are identical to that of the structure D_3d. The values of Torques for both structures are very close to zero and this assures that these two structures converge to the structure D_3d and this assure with old studies [14].

Table 1: Total relative energies (kcal/mol) for Be(BH₄)₂.

 

The studying of electron diffraction (ED) by Bauer for Beryllium borohydride assure the structure of D_3d while the previous diffraction proved that the structure D_2d is the stable shape for Berilium borohydride and thus the structure D_2d is the best [15].

When we compared the calculated bonds for Be(BH₄)₂that we obtained in table 2 with the bond lengths of identical borohydrides obtained from of studies [16-19], we find that these compounds tend to have ionic property more than covalent property because the lengths of bonds for these compounds is near to the values of length of ionic borohyaridesbonds like LiBH₄, NaBH₄Table 3.

Table 2: Geometrical Parameters in Aͦ of Be(BH₄)₂.

 

Table 3: Geometrical parameters in Aͦ for M(BH₄)_n.

	M-B	M-Hb	B-Hb	B-Ht
NaBH4	2.2100	2.1600	1.2600	1.1600
LiBH4	2.2230	2.1730	1.2560	1.1700
Al(BH4)3	2.1430	2.0100	1.2830	1.1960
Zr(BH4)4	2.1000	1.7400	1.9200	1.1950

 

Vibrational Spectra

After calculating wave numbers, infrared intensities and Raman scattering activities for D_2d, D_3d, Cs and C_3v for the vibrational fundamentals of Be(BH₄)₂ at all levels were calculated by using the same basis sets. We obtained the best results at the B3LYP/6-311++G(d,p) level as explained in the Table 4. From these results, we observe that vibrations with high energy of Tetra borohydride are vibrational tensions to the bond between Boron atom and terminal hydrogen atom. This bundle appears in the IR spectra at (2647 cm^-1). While it appears in Raman spectra at (2605 cm^-1), these results agree with results of Nibler for Beryllium borohydrides. The tension bundle appeared in IR spectra at (2627 cm^-1) [20, 21].

From Table 4, we observe that the position of bundle in IR spectra and Raman spectra which we obtained by using Ab initio methods at B3LYP/6-311++G(d,p) level have very near values. This is primarily due to the nature of the structure of borohydrides which contain two identical BH₄ groups and this leads to the appearance of vibrational motion in reverse (op) in IR spectra and the vibrational motion in the same phase (ip) in Raman spectra.

The vibrational bundles which appear in the region (2100-1400 cm^-1) are due to the stretching of hydrogen tied bonds in ring shape (bridging hydrogen); it is found that if the compound is more ionic, the bands move gradually outside this region and some of them take higher values gradually outside this area and become (stretching vibration). Furthermore, the other take lower values and become deformation vibration [22] and this agrees with the results which are studied before these bands appear in IR spectra of B₂H₆ at (1990-1850 cm^-1) and (1600 cm^-1) and incase of Be(BH₄)₂ it will appear at (2165- 1985 cm^-1) and (1530 cm^-1) . As in the case of B₂H₆, the bands are clearer in spectrum with higher intensity. This is because of the bridging hydrogen considered as a base for the decrease of electrons and the shifted atoms in this region are able to make large dipole [22].

The theoretical results of vibrational motion are obtained in this study by using Ab initio methods and the two stretch bands which are the result of the vibrational bond B- H_b appeared in IR spectra at (2573 cm^-1) and (2574 cm^-1); the first is characterized by symmetric stretching and the second is characterized by the asymmetric stretching. In Raman spectra, the two bands appear at (2573 cm^-1) and (2575 cm^-1) in the symmetric stretching and asymmetric stretching consequently. This agrees with the results of previous studies [21]. The bending of B- H_b bond at (351 cm^-1) in IR spectrum and (353 cm^-1) in Raman spectrum is identical to the experimental results which are obtained in previous studies for the same compound.

This band appears in IR spectra at (287 cm^-1) for Be(BH₄)₂ [20]and in another study [21]and at (368 cm^-1) for the same compound. Two bands appear in the region B-M-B; the first is for the Stretching Vibration of B-M-B bond and appears at (600 cm^-1) and the other is a bending to this bond and appears at (400 cm^-1). In this study, we found that the band of Stretching Vibration of B-Be-B bond appears at (550 cm^-1) while the bending of the bond give a band at (421 cm^-1) and these values are in agreement with the experimental studies that made before [20].

The band of BH wag appears at (1622 cm^-1), (1666 cm^-1) in IR and Raman spectra consequently by using the basic sets 6-311++G(d,p) at the level B3LYP from the theory.

Vibrational bond B- H_b deformation appear at (1169 cm^-1) and (1283 cm^-1). The first is vibration symmetric deformation and the second involves vibration form asymmetric deformation at in the same phase (ip). This shows both bands at (1173 cm^-1) and (1236 cm^-1) to symmetric deformation and asymmetric deformation at the same phase (op) respectively using the basic sets 6-31++G(d,p) at the level B3LYP from the theory.

Table 4: frequencies and Infrared Intensities Calculated for the Vibrational Fundamentals of Be(BH₄)₂ Using Gaussian at the B3LYP/6311++G(d,p) level.

Vibrational modes	frequencies (cm-1)	IR Intensities	Raman scattering activities	Approximate modedescription
E
ν1	421.1826	14.0137	0.0000	B-Be-B bend
ν2	351.5320	13.8284	0.0000	BHb asym bend
ν3	1173.8077	3.4603	0.0000	BHb sym deform (op)
ν4	1622.5912	0.8385	0.0000	BH wag (op)
ν5	2574.4237	3.4556	0.0000	BHb asym str (op)
ν6	2573.0759	96.0812	0.0000	BHb sym str (op)
ν7	2647.6727	75.2938	0.0000	BHt str (op)
A1
ν8	550.3760	0.0000	16.9146	B-Be-Bsym str
ν9	353.2426	0.0000	17.5656	BHb sym bend
ν10	1169.2697	0.0000	14.4690	BHb sym deform (ip)
ν11	2575.7881	0.0000	100.1102	BHb asym str (ip)
ν12	2605.7573	0.0000	316.0911	BHt str (ip)
B1
ν13	545.0395	0.6523	0.0000	B-Be-B asym str
ν14	1236.9411	34.3443	0.0000	BHb asym deform (op)
B2
ν15	1666.0020	0.0000	0.1855	BH wag (ip)
ν16	1283.5967	0.0000	38.0773	BHb asym deform (ip)
ν17	2573.6717	0.0000	72.0237	BHb sym str (ip)
A2
ν18	1130.1214	0.0000	0.0000	BH4 torsion

 

Conclusion

From the theoretical result on beryllium borohydride Be (BH₄)₂ which are obtained, we can conclude that

1. The structure D_2d which contains two identical groups of double bridging hydrogen has low energy at all levels of study so we consider it as the most stable structure for Be(BH₄)₂.
2. Both two structures C_S, C_3V have the structure of D_3d kind at all levels. The values of bond lengths for these two structures are identical for the bond lengths to the structure D_3d kind assure this theory.
3. The theoretical results of IR and Raman spectra which are obtained by using different methods to approach the energy of the system with basic different showed that the best results are groups obtained at the level B3 LYP with using the basic set 6-311++G(d,p) and all these results prove that the structure D_2d is for Be(BH₄)₂.

References

1. Almenningen, A.; Gundersen, G.; Haaland, A. Acta Chem. Scand. 1968, 22, 328.
   CrossRef
2. Coe, D. A.; Nibler, J. W. Spectrochim. Acta 1973, 29A, 1789.
   CrossRef
3. Plato, V.; Hedberg K. Inorg. Chem. 1971, 10, 590.
   CrossRef
4. Mancini, M.; Bougeard, P.; Burns, R. C.; Mlekuz, M.; Sayer, B. G.; Thompson, J. I.; McGlinchey, M. J. Inorg. Chem. 1984, 23, 1072.
   CrossRef
5. Hori, K.; Saito, G.;Teramae, H. J. Phys. Chem. 1988, 92(13), 3796.
   CrossRef
6.  Marks, T. J.; Kolb, J. R. Chem. Rev. 1977, 77, 263.
   CrossRef
7. Marks, T. J.; Kennelly, W. J.; Kolb, J. R.; Shimp, L. A. J. Inorg. Chem. 1972, 11, 2540.
   CrossRef
8. Ortiz, J. V.; Lipscomb, W. N. In AIP Conference Proceedings (American Institute of Physics) New York, 1986.
9. Ahlrichs, R. Chem. Phys. Lett. 1973, 19, 174.
   CrossRef
10.  Stanton, J. F.; Lipscomb, W. N.; Bartiett, R. J. J. Chem. Phys. 1988, 88(9), 5726.
    CrossRef
11.  Marynick, D. S.; Lipscomb, W. N. J. Am. Chem. Soc. 1973, 95(22), 7244.
    CrossRef
12. Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb, M. A.; Cheeseman, J. R.; Montgomery, J. A., Jr.; Vreven, T.; Kudin, K. N.; Burant, J. C.; Millam, J. M.; Iyengar, S. S.; Tomasi, J.; Barone, V.; Mennucci, B.; Cossi, M.; Scalmani, G.; Rega, N.; Petersson, G. A.; Nakatsuji, H.; Hada, M.; Ehara, M.; Toyota, K.; Fukuda, R.; Hasegawa, J.; Ishida, M.; Nakajima, T.; Honda, Y.; Kitao, O.; Nakai, H.; Klene, M.; Li, X.; Knox, J. E.; Hratchian, H. P.; Cross, J. B.; Adamo, C.; Jaramillo, J.; Gomperts, R.; Stratmann, R. E.; Yazyev, O.; Austin, A. J.; Cammi, R.; Pomelli, C.; Ochterski, J. W.; Ayala, P. Y.; Morokuma, K.; Voth, G. A.; Salvador, P.; Dannenberg, J. J.; Zakrzewski, V. G.; Dapprich, S.; Daniels, A. D.; Strain, M. C.; Farkas, O.; Malick, D. K.; Rabuck, A. D.; Raghavachari, K.; Foresman, J. B.; Ortiz, J. V.; Cui, Q.; Baboul, A. G.; Clifford, S.; Cioslowski, J.; Stefanov, B. B.; Liu, G.; Liashenko, A.; Piskorz, P.; Komaromi, I.; Martin, R. L.; Fox, D. J.; Keith, T.; Al-Laham, M. A.; Peng, C. Y.; Nanayakkara, A.; Challacombe, M.; Gill, P. M. W.; Johnson, B.; Chen, W.; Wong, M. W.; Gonzalez, C. and Pople, J. A. Gaussian 03, Revision B.04; Gaussian, Inc.: Pittsburgh, PA 2003.
13. Gilliard Jr. Robert J.; Abraham, Mariham Y.; Wang, Yuzhong; Wei, Pingrong; Yaoming, Xie; Quillian, Brandon; Schaefer III, Henry F.; Schleyer, Paul v. R.; Robinson, Gregory H.  J. Am. Chem. Soc 2012, 134, 9953.
14. Baranov, L. Ya.; Boldyrev, A. I. Chem. Phys. Lett. 1983, 96, 218.
    CrossRef
15. Bauer, S. H. J. Am. Chem. Soc. 1950, 72, 622.
    CrossRef
16. Barone, V.; Dolcetti, G.; Lelj, F.; Russo, N. J. Inorg. Chem. 1981, 20(6), 1687.
    CrossRef
17. Defrees, D. J.; Raghavachari, K.; Schlegel., H. B.; Pople, J. A.; Schleyer, P. V. R. J. Phys. Chem. 1987, 91, 1857.
    CrossRef
18. Charkin, O. P., Musaev, D., G. and Klimenko, M. N. Koord. Khim 1985, 11, 409.
19. Barone, V.; Minichino, C.; Lelj, F.; Russo, N. J. Comput. Chem. 1988, 9(5), 518.
    CrossRef
20. Nibler, J. W. J. Am. Chem. Soc. 1972, 94(10), 3349.
    CrossRef
21. Nibler, J. W.; Shriver, D. F.; Cook, T. H. J. Chem. Phys. 1971, 54(12), 5257.
    CrossRef
22. Rice, W. C. J. Chem. Phys. 1949, 17(11), 1044.
    CrossRef

---

This work is licensed under a Creative Commons Attribution 4.0 International License.