Isolobal Series of Chemical Fragments
Enos Masheija Kiremire
Department of Chemistry and Biochemistry University of Namibia, Private Bag 13301, Windhoek, Namibia. Corresponding Author Email: kiremire15@yahoo.com
DOI : http://dx.doi.org/10.13005/ojc/31.Special-Issue1.07
Article Received on :
Article Accepted on :
Article Published : 10 Sep 2015
During the study of carbonyl clusters using 14n and 4n rules, it was discovered that fragments and atoms could be categorized. This paper presents the categorization of isolobal fragments, molecules and ions using the 14n and 4n rules. In the process of categorization, the conventional periodic table was recreated. A new method of categorizing clusters using fragments and series has been introduced for the first time and this immensely simplifies the categorization of clusters from simple to more complex ones including boranes, carboranes, transition metal carbonyls and metalloboranes. The paper also introduces a simple algebra of cluster series.
KEYWORDS:carbonyl clusters; metalloboranes; Isolobal Series;
Download this article as:| Copy the following to cite this article: Kiremire E. M. Isolobal Series of Chemical Fragments. Orient J Chem 2015;31(Special Issue1). |
| Copy the following to cite this URL: Kiremire E. M. Isolobal Series of Chemical Fragments. Orient J Chem 2015;31(Special Issue1). Available from: http://www.orientjchem.org/?p=10740 |
Introduction
The arrival of Hoffman’s isolobal principle greatly assisted the advancement of chemical knowledge of linking up the inorganic, organic and organometallic fields1-2.. A combination of isolobal principle and Wade-Mingos rules3-4 laid a strong base for cluster chemistry of boranes, carboranes and transition metal carbonyls. It has recently been found that the organic, and many inorganic and organometallic compounds and clusters follow the 4n and 14n series5-6. In continuing to examine the application of the series in analyzing chemical structures, it has been discovered that the isolobal principle also follows the 4n and 14n series. This revelation is presented in this paper.
Results and Discussion
In the study of osmium carbonyl clusters7, it was found that some of the series follow a pattern in which one carbonyl ligand is removed at every step until a given cluster is completely stripped naked. In the Hoffmann’s isolobal principle the initial fragment molecule used is methane, CH4. The stripping off one H atom creates CH3 fragment. The next stages produce the fragments CH2, CH and finally the naked C is the final product. Using the 4n rule of classification1-2 the CH4 molecule or fragment belongs to 4n+4 series, while the CH3 belongs to 4n+3 series, CH2 is a member of 4n+2 series, CH is a member of 4n+1 series and C belongs to 4n series. The series give the value of the electron content of the fragment. For example in CH4 , n = 1, the series value S = 4n+4 = 4×1+4 = 8, CH3, S = 4n+3, n =1, S = 7, CH2 , S = 4n+2, n= 1, S = 6, CH, S = 4, and C, S=4. In terms of series, what is found interesting is that these values correspond to the respective valence content of the fragments. The CH3 fragment was found to be isolobal with Mn(CO)5 fragment. Also applying the 14n rule of classification, Mn(CO)5 fragment belongs to 14n + 3 series. The 14n +3 series and 4n+3 series while they are not identical, they are similar. If n =1 for the fragment Mn(CO)5, then S = 14n+3 = 14×1+3 =17, the valence content of the fragment (7+5×2=17). When 10 n is subtracted from 14n+3 it becomes 4n+3. This means if 10n = 10×1 = 10 is removed from 17, then 7 is left which is the same as the valence content of CH3. Thus, the two fragments CH3 and Mn(CO)5 are interrelated by series. Accordingly, the fragments are truly isolobal CH3 ⥈ Mn(CO)5. In this paper, 14n + q and 4n+q will be used interchangeably as needed.
 |
Table 1: Classification of Isolobal Fragments into Series Click here to View table |
The Recreation of the Periodic Table
What is fascinating and exciting is that the use of 14n and 4n rule the Periodic Table of Elements and Fragments has been created. For the ordinary elements of the periodic table they have been placed precisely into their usual places while the isolobal fragments have been classified and placed side by side with the ordinary elements into equivalent periodic groups. This table has implications. For example, if CH fragment may be regarded as equivalent to N atom, it implies that the H atom acted as an electron donor to the the carbon atom(C) making it have 5 valence electrons in the (CH) fragment like the nitrogen atom (N) and hence placing it into group 5 or 15 like the nitrogen atom. In the same manner, in the fragment [Cr(CO)] when the CO ligand donates the two electrons to Cr which is in group 6 of the transition elements it makes it behave as if it is an iron atom(Fe) atom of group 8. On the basis of the series, it appears that the basis of the isolobal principle is the electron content of the sum valence electrons around the skeletal atom. In the case of CH3 fragment, the carbon has 4 valence electrons and the three hydrogen atoms donate three more electrons making the carbon atom have a surrounding environment of 7 valence electrons. Thus, it acquires the status of a group 7 element such as fluorine. Group 7 has other family members such as Cl, Br, and I. Moving along the period from C the next element is nitrogen atom(N). The addition of 2H atoms converts it NH2 which also has a total valence content of 7. The NH2 fragment will also be isolobal to CH3. Since N is in group 5, other family members namely, PH2, AsH2, SbH2, and BiH2 will also be isolobal to CH3. In case of group 17, those elements with carbonyls will also be isolobal to CH3. Since we are actually comparing parallel series 14n+3 with 4n+3, if we remove 10n from 14n+3 we will convert the carbonyl series to main group series of 4n+3. Futhermore, since we are dealing with a single skeletal element, then 10n is equivalent to 10×1 = 10. Hence, if we subtract 10 from 17 we will get 7 the valence electron content of CH3 fragment and group 7 elements. The carbonyl fragments include the hypothetical and real ones such as V(CO)6, Nb(CO)6, Ta(CO)6, Mn(CO)5, TcCO)5, Re(CO)5, Co(CO)4, Rh(CO)4, Ir(CO)4, Cu(CO)3, Ag(CO)3 and Au(CO)3. The fragments from the main group elements and transition metal fragments which are isolobal to CH2 and CH fragments corresponding to 6 and 5 valence electrons can similarly be identified. Again the removal of 10 electron units from the carbonyl fragments will yield the corresponding 6 and 5 valence electron contents. It should be pointed out that the hydrogen atom can be replaced by an alkyl group, R or aryl group Ar. The selected isolobal extended family members are indicated in Tables 2 to 4. In searching for possible isolobal fragments for CH3 from main group elements, numbers could act as a guide. For example since we are looking for seven valence electrons, we may use sets such as (4+3) this can lead us to group 4 elements combined with 3 hydrogen atoms. Hence, we generate, CH3, SiH3, GeH3, SnH3, and PbH3. In the case of transition metals, we want to generate 17 electron systems. The set of numbers we may need for example could include (5+12). This set will give us the carbonyl fragments such as V(CO)6, Nb(CO)6, and Ta(CO)6, while the set (7+10) could give us the carbonyls M(CO)5, M = Mn, Tc, and Re. The combination (9+8) will generate M(CO)4 where M = Co, Rh, and Ir. The other possible combination of numbers to give 17 is (8+5+4). This set will generate the fragments such M(Cp)(CO)2 where M = Fe, Ru and Os and Cp = η5-C5H5.
| Table 2: Selected CH3 Isolobal Family | ||||||||
| GROUP 17 | GROUP 7 | |||||||
| 14n+3 SERIES | 4n+3 SERIES | |||||||
| Cu(CO)3 | Co(CO)4 | Mn(CO)5 | V(CO)6 | CH3 | CH3 | NH2 | OH | F |
| Ag(CO)3 | Rh(CO)4 | Tc(CO)5 | Nb(CO)6 | SiH3 | PH2 | SH | Cl | |
| Au(CO)3 | Ir(CO)4 | Re(CO)5 | Ta(CO)6 | GeH3 | AsH2 | SeH | Br | |
| SnH3 | SbH2 | TeH | I | |||||
| PbH3 | BiH2 | |||||||
| 11+6 =17 | 9+8 = 17 | 7+10 =17 | 5+12 =17 | 4+3 =7 | 5+2 =7 | 6+1 = 7 | 7 | |
| 17-10 =7 | 17-10 = 7 | 17-10 =7 | 17-10 = 7 | |||||
Table 3: Selected CH2 Isolobal Family
| GROUP 16 | GROUP 6 | ||||||
| 14n+2 SERIES | 4n+2 SERIES | ||||||
| Zn(CO)2 | Ni(CO)3 | Fe(CO)4 | Cr(CO)5 | CH2 | CH2 | NH | O |
| Cd(CO)2 | Pd(CO)3 | Ru(CO)4 | Mo(CO)5 | SiH2 | PH | S | |
| Hg(CO)2 | Pt(CO)3 | Os(CO)4 | W(CO)5 | GeH2 | AsH | Se | |
| 12+4 =16 | 10+6 =16 | 8+8 = 16 | 6+10 =16 | SnH2 | SbH | Te | |
| PbH2 | BiH | ||||||
| 16-10 =6 | 16-10 = 6 | 16-10 = 6 | 16-10 = 6 | 4+2 = 6 | 5+1 = 6 | 6 | |
| Table 4: Selected CH Isolobal Family | |||||
| GROUP 15 | GROUP 5 | ||||
| 14n+1 SERIES | 4n+1 SERIES | ||||
| Cu(CO)2 | Co(CO)3 | Mn(CO)4 | CH | CH | N |
| Ag(CO)2 | Rh(CO)3 | Tc(CO)4 | SiH | P | |
| Au(CO)2 | Ir(CO)3 | Re(CO)4 | GeH | As | |
| 11+4 = 15 | 9+6 = 15 | 7+8 =15 | SnH | Sb | |
| 15-10 =5 | 15-10 = 5 | 15-10 = 5 | PbH | Bi | |
| 4+1 = 5 | 5 | ||||
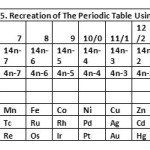 |
Table 5: Recreation of The Periodic Table Using Series Click here to View table |
Arising from the arranging isolobal fragments and elements according to series as indicated in Table 1, it became apparent that the 14n and 4n series were in fact recreating the Periodic Table of Elements as is currently known. A portion of this is portrayed in Table 5. Since we are considering one skeletal element in this case, n = 1 and this generates the numbers in the first row of the table. These findings are fascinating.
Assembling the Fragments
As can be seen from Table 1, atoms and fragments can be categorized according to series. In actual fact, what has happened in Table 1, the 14n and 4n series have created or reproduced a Periodic Table of elements and fragments. Just as atoms can be assembled according to valence rules to produce molecules, fragments can do the same. Scheme 1 gives some few illustrative examples. Fragments can be combined to generate molecular structures. Let us illustrate this concept starting with the simplest fragment CH3. This fragment belongs to 4n+3 series. Adding two of these fragments is equivalent to 2[CH3(4n+3)] = C2H6 (4n+6). Thus, the multiplication affects the digit component of the series (2×3 = 6) but not the 4n component. In actual fact the 4n represents the number of the valence electrons contributed by the carbon skeletal atoms and the digital part represents the hydrogen atoms contribution to the valence account. In this result, when n =2, the value of the series S= 4n+6 = 4×2+6 = 14, which the sum of the valence electrons of C2H6.. This means that in series, the rule is that the the addition or multiplication does not affect the (4n) component of the series. The digit portion is the one to be added or subtracted whatever the case maybe. This makes sense because 4n for n =1 gives us 4 while 4n for n =2 gives us 8. This gives us a simple algebraic rule of adding series. Let us take CH2 fragments for illustrating the concept combining series. The fragment CH2 belongs to 4n+2 series.
 |
Scheme 1: Combination of two Isolobal Fragment Click here to View scheme |
The value k =2n-x where = 0, 1, 2,3, 4 and son comes from a simple correlation of the empirical observation of the number of skeletal atoms involves and the corresponding digit of the molecular fragment series formed. Thus, in the case of C2H6, we know it has a single C-C bond and 2 skeletal atoms. In order to create a simple mathematical relationship of a single bond with the series S = 4n+6, it is common sense that k = 2n-3. The digit 3 is just one half of 6 and n represents the number of the skeletal atoms. Naturally for N2 with S = 4n+2, the k value is given by 2k-1 =3, the triple bond of dinitrogen as we know it. In this way, a simple mathematical relationship between skeletal bonds or linkages and the corresponding number of skeletal atoms is developed. Let us try one example to illustrate the concept of assembling fragments. We can combine 4 fragments of Ir(CO)3 as follows.
4[Ir(CO)3] = Ir4(CO)12.
4[14n+1, n = 1] = 14n+4 (n = 4); k = 2n-2 = 2×4-2 = 6.
4[14X1+1 =15] = 14X4+4 = 60 = V. This the number of valence electrons of the cluster and k =6 is the cluster number
in this case. It also corresponds to the number of linkages of the skeletal atoms which have a tetrahedral geometry (Td) as sketched in Figure 1. Since the 14n series run parallel to the 4n series, the removal of 10 n electrons from V = 60 will give us the number of valence electrons characteristic to corresponding cluster of the main group elements. In this case 60-10×4 = 20. This number of valence electrons can give us a (CH)4 , P4 or (BH)4 cluster with the ideal Td symmetry.
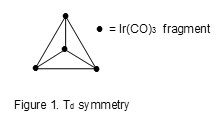
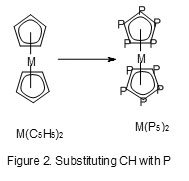
Isolobal fragments may be considered to contain the same number of valence electrons and hence can be substituted in similar chemical species. A typical example is Ir(CO)3 0↔CH. Complete substitution of Ir(CO)3 by CH will produce a Td geometry as in Figure 1. In C5H5 = (CH)5, the CH may be replaced by P to produce P5 fragment. Therefore C5H5― C0↔ P5―. This implies that M(C5H5)2 equivalent clusters M(P5)2 where M represents a metal atom such as Fe or Ru may be synthesized. The result is depicted in Figure 2.
Unique Simplification And Structure Prediction Using Isolobal Principle And Series
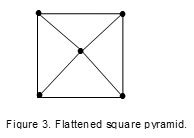
The most fascinating and exciting aspect of isolobal principle in combination with series is the way they can simplify an apparently imposing cluster to a bare simple number from which its structure (shape) can be predicted with high accuracy. Let us consider the carbonyl cluster, Ru5(C)(CO)15 which has a square pyramid geometry8. Applying the isolobal principle and series, we can split up the cluster into simpler mono-skeletal fragments as follows. The splitting of molecule into fragment, the nature of monoskeletal fragments produced does not matter as long as you can readily work out their corresponding fragmental series. Let us represent the molecular formula with F = Ru5(C)(CO)15 = 5[Ru(CO)3] + C. For Ru(CO)3 fragment; V = 8 +3×2 = 14 valence electrons, and n =1, hence 14n =14. Therefore the fragment belongs to S = 14n +0 series. The approach is to determine the overall cluster series (SF) of the formula F. If regard the C atom as a donor of its valence electrons and not part of the skeletal cluster fragment, then the overall series of the formula F is obtained in a straight forward manner. 5[Ru(CO)3] → SF = 5[14n+0] + 4 = 14n +4 where n = 5. Therefore the series SF = 14n +4 tells us that the cluster is a member of the NIDO family. A nido structure is just one step awy from being a closo (the ideal of full or standard) geometry. In this case,an M-5 skeletal fragment is one step away from an ideal M-6 octahedral (closo) symmetry. For the main group elements, this series is the same as that of SF = 4n+4. Furthermore, it also gives us the valence content of the cluster if we substitute n =5 in the formula series. Just like the 4n+4 series, the cluster k value is obtained from k =2n-2 = 2×5-2 = 8. This implies that an M-5 skeletal cluster with k = 8 has a characteristic shape of a square pyramid sketched in Figure 3. The shape is flattened for ease of visibility. The borane cluster B5H9 is known to have an ideal square pyramid shape6. We can readily determine its series by splitting up into mono-skeletal fragment as we please and deduce the series of each fragment. Then finally sum up the series to get the formula series of B5H9. This is illustrated below.
B5H9 = [BH]+ 4[BH2]
[BH] , V = 3+1 = 4, n = 1, 4n = 4, S = 4n + 0
[BH2] , V = 3+2 = 5, n = 1, 4n = 4, S = 4n +1.
4[BH2], V = 4[4n+1] = 4n + 4 .
SF = (4n+0)+4(4n+1) = 4n+4, for n = 5, S = 24, the number of valence electrons of B5H9. The k value = 2n-2 = 2×5-2 = 9. Hence , this is an M-5 cluster with k=8, and with an ideal square pyramid shape as is already known.
Let us now tackle the [(Cp)Co][B4H8] cluster. The cluster can be split into fragments as follows.
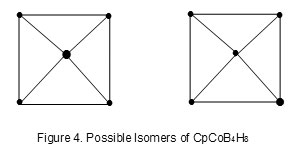
[(Cp)Co][B4H8] = [CpCo][BH2]X4; [CpCo], V = 5+9 = 14, n = 1, 14n = 14. Hence, S = 14n+0 = 4n+0. [BH2], V = 3+2 = 5, n =1, 4n +1. Hence, 4[BH2] = 4[4n+1, n =1] = 4n+4 (n =4). SF = (4n+0) +(4n+4) = 4n+4 (n =5). Therefore the formula, for the series SF = 4n+4 (n =5) = 24 if Co is regarded as main group element. Since the main group skeletal elements are more than the coordinated metal atoms in the metalloborane complexes,it is best to regard to consider them as if they belong to the main group elements. With SF = 4n+4 for the [(Cp)Co][B4H8] cluster, then k = 2n-2 = 2×5-2 = 8. Since the cluster has 5 skeletal elements M-5 and has k = 8, its ideal shape will be a square pyramid. The presence of a metal atom, makes it possible for the M-5 cluster to have two possible isomers as sketched in Figure 4. Again the square pyramid geometry has been flattened to allow a better visibility. The larger point in the sketch represent CpCo fragment and Cp = C5H5.
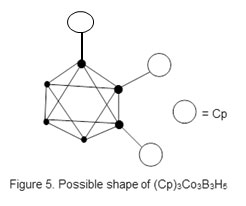
Let us try a few more examples to demonstrate the power of fragments and series in predicting the geometry by considering the example (Cp)3Co3B3H5 cluster8. The cluster can be fragmented into 3[CpCo]+[BH]+ 2[BH2] units. The series for each fragment can be worked out and the total series for the cluster easily obtained. This is shown in Scheme 2. With a cluster of M-6 and k =11 belonging to the 4n+2 series (CLOSO), the geometry is predicted to be an octahedral which is the case. A possible skeletal shape is sketched in Figure 5.
 |
Scheme 2: Example for Determining Cluster Series Using Fragments Click here to View scheme |
Consider the cobalt cluster (CpCo)2(C2B6H8)8. Its structure can readily be deduced by use of fragments and series approach. The formula of the cluster can be re-written as follows (CpCo)2(CH)2(BH)6. The [CpCo] fragment with 14 electrons belong to 14n ( = 4n+0) series. The 6 BH fragments also belong to the 4n series. However the two CH fragments contribute 2[4n+1] = 4n+2 towards the series. The net series of the cluster SF = 2[4n+0] + 6 [4n+0] +2[4n+1] = 4n+2 series for n =10. Hence, the final series is SF =4n+2. This means the cluster belongs to CLOSO series. Since n =10, it will have a shape similar to that of B10H102―.This skeletal structure is given in Figure 6 with two of the ten atoms being cobalt atoms carrying the Cp (C5H5) rings. Since, the use of series to predict shapes is not common, let us briefly restate them. The S = 4n+2 is closo, 4n+4 (nido), 4n+6(arachno), 4n+8(hypho). 4n+10 (klapo) and so on. But for 4n+0 (monocapped), 4n-2(bicapped), 4n-4(tricapped), 4n-6(tetracapped) and so on. In the case of the capped series the k value takes a positive number after the n, thus k = 2n+1 for bicapped series, k = 2n+2 for tricapped series and so on.
 |
Figure 6,7 Click here to View figure |
 |
Scheme 3 Click here to View scheme |
Revisiting the Rudolph Correlation System of Clusters
A lot of work has been done on boranes and its relatives mainly carboranes, and metalloboranes as well as transition metal carbonyl clusters1-2,. The prediction of shapes of these clusters is based mainly on the well known Rudolph correlation system also based on known shapes 12-13. For example, if an M-5 skeletal system is an arachno, then it is traced to an M-7 closo system whose shape is known (pentagonal bipyramid) in order to derive its shape by correlation. However, if M-5 system is a Nido one, it is related to the next M-6 (octahedral) closo system. This correlation system is presented in formula form in Table 6. It is quite clear that the Rudolph correlation system is a DECAPPING SYSTEM which is characterized by change in k value by 3. For example from B6H62−(B6H8) of k =11 to B5H9( k= 8) to B4H10( k = 5). On the other hand if we know the k-value of a given M-x cluster, we can use that as a guide to predict the shape. For instance B5H11 (M-5) with k =7 and of 4n+6 series, will be a Nido and with a shape deduced from the k value or correlation with k =11 an octahedral closo shape. On the other hand if B5H9(M-5, k =9). This predicted to be a trigonal bipyramid. It must be pointed out that the 4n+2 series are known to exist in ionic form. For example, B5H7 exists as B5H52−and B6H8 as B6H62−. If the type of cluster series of a given formula is known, then the k value is readily calculated. For instance, B9H13 if we write it as (BH2)4(BH)5 fragments, we can readily deduce its series. Thus; 4[BH2]+5[BH] = 4[4n+1] +5[4n+0] = 4n+4. In the algebra of series, the 4n remains constant regardless of the multiplier. What changes is the value of the digit after 4n (or 14n). Also additions of 4n do not change it. Hence, 4[4n+1] simply becomes 4n+4 as the multiplier (4) does not affect it. However, the multiplier affects the digit and so we get, 4×1 =4. Similarly, 5[4n+0] becomes 4n+0 as the multiplier 5 does not affect 4n and 5×0 = 0. When (4n+4) is added to (4n+0), the result becomes 4n+4 as the addition does not affect the 4n term but the digits 4+0 = 4. The net result is S = 4n+4 the series for B5H9 borane cluster. If n = 5 for a 5-skeletal cluster, the value of S becomes S = 4×5+4 = 24. This the sum of valence electrons for B5H9. This can be verified from 5×3+9 = 24 as derived from the formula. In order to get more familiar with the power of deducing the series of a given molecular formula , let us take B6H10 cluster. There are several ways of splitting it up into fragments. But let us consider one of them given in Scheme 4. The B6H10 cluster was split into (BH)2(BH2)4 and then the series of each fragment was determined. Hence, the overall series of the cluster easily deduced. It is amazing and delightful to see how the combination of fragments and series work together to readily decompose a seemingly complex formula into its family of series. Once the cluster series has been deduced, it becomes quite easy to predict it shape in the usual way. The ideal skeletal shape of B6H10 is shown in Figure 7.
| Table 6: Rudolph Correlation Scheme | ||||
| 4n+2 | 4n+4 | 4n+6 | ||
| k=2n-1 | k =2n-2 | k = 2n-3 | ||
| CLOSO | NIDO | ARACHNO | ||
| B2H4(3) | BH5 | |||
| B3H5(5) | B2H6(2) | BH7 | ||
| B4H6(7) | → | B3H7(4) | → | B2H8(1) |
| B5H7(9) | → | B4H8(6) | → | B3H9(3) |
| B6H8(11) | → | B5H9(8) | → | B4H10(5) |
| B7H9(13) | → | B6H10(10) | → | B5H11(7) |
| B8H10(15) | → | B7H11(12) | → | B6H12(9) |
| B9H11(17) | → | B8H12(14) | → | B7H13(11) |
| B10H12(19) | → | B9H13(16) | → | B8H14(13) |
| B11H13(21) | → | B10H14(18) | → | B9H15(15) |
| B12H14(23) | → | B11H15(20) | → | B10H16(17) |
| Scheme 4: Using Fragments and their Series to Categorize B6H10 into its Family Series | ||||
| B6H10 | ||||
| FRAGMENT | 4n( n = 1) | VALENCE ELECTRONS | SERIES | |
| 4X1 =4 | ||||
| BH | 4 | 3+1 = 4 | 4n+0 | |
| BH | 4 | 3+2= 5 | 4n+0 | |
| BH2 | 4 | 3+ 2= 5 | 4n+1 | |
| BH2 | 4 | 3+ 2= 5 | 4n+1 | |
| BH2 | 4 | 3+ 2= 5 | 4n+1 | |
| BH2 | 4 | 3+ 2= 5 | 4n+1 | |
| FINAL SERIES (SF) = | 4n+4 | |||
| CONCLUSION = NIDO SERIES | ||||
| k = 2n -2 = 2(6)-2 = 10 | ||||
| SHAPE = PENTAGONAL PYRAMID | ||||
Conclusion
This paper is a climax of intense efforts in an attempt to fully understand and be able to explain structures of clusters of the main group elements and transition metal carbonyls in much simpler way than is currently presented. The work started with the introduction of cluster number (k value ) which led to the establishment of 14n and 4n rules14-15. It was demonstrated that clusters could easily be categorized by using the 14n and 4n rules5-6. Further investigations into the nature of carbonyl clusters with respect to capping series led to the revelation that molecules, fragments, atoms could be categorized by 14n and 4n rules7. This sparked great interest in applying the 14n and 4n rules to Hoffmann’s isolobal fragments. This has proved a tremendous success as it was discovered that isolobal fragments, molecules were interlinked by 14n and 4n rules and that they could be categorized in the same way as elements in the periodic table. Furthermore, what is interesting was that the placement of fragments and elements resulted in recreating the modern periodic table. It became easier to appreciate why a fragment such as Os(CO)4 of a transition behaved like CH2 of the main group elements. The reason being Os(CO)4 fragment has a CH2 fragment belongs to the 4n system. If 10 electrons are removed from 16 electrons of the Os(CO)4 fragment the remainder is 6 electrons corresponding to those of the CH2 fragment. It is as if another CH2 fragment is hiding within Os(CO)4 fragment. Finally, when the concept of fragments and series are applied to clusters they are easily reduced to simple series from which cluster structure can be predicted in the usual way. What is much more heart- warming and pleasant was that not only does the 14n and 4n rules reproduce Mandeleev’s periodic table of elements, categorize Hoffmann’s fragments into their positions in the periodic table, but it also provides us with the basis for OCTET RULE AND EIGHTEEN ELECTRON RULES that have played vital roles in science. If we look carefully at Table 1 column 18//8, we can discover all those fragments listed there possess an element that obeys either octet rule or 18-electron rule. For instance, HF, OH2, NH3,CH4, and BH5 obey the octet rule while Ne, Cr(CO)6, Mo(CO)6, W(CO)6, Fe(CO)5, Ru(CO)5, Os(CO)5, Ni(CO)4, Zn(CO)3 and Cd(CO)3 in principle obey the 18-electron rule. Since atoms, fragments and molecules can be categorized into series and they can also be combined to produce other fragments and molecules and in turn can be split up into fragments, this implied that the corresponding series of fragments can somehow also be maneuvered. Indeed a simple algebra of series has briefly been introduced to simplify the categorization of clusters. In the author’s reflections and meditations, seeing the beauty and smooth flow of using simple numbers to generate these results with no heavy computational calculations, D. Mendeleev(1834-1907), I. Langmuir(1881-1957), G.N. Lewis(1875-1948) and even R. Hoffmann (1937-) would smile broadly at how nature is so wonderful. This work complements the existing knowledge on clusters whose skeletal elements obey the 18 or 8 electron rules.
Acknowledgement
The author wishes to acknowledge the financial and material resources provided towards this work, the NAMSOV company, Namibia for its generous funding and my wife Merab Kambamu Kiremire for her tireless encouragement to write this paper.
References
- Hoffmann, R., Angew. Chem. Int. Edition, 1981, 21(10), 711-724.
- Miessler, G. L., Fischer, P. J., Tarr, D. A., ‘Inorganic Chemistry’, 5th Edition, Pearson, New York, 2014.
- Wade, K. ,J. Chem. Soc., Dalton, 1971, 792-793.
- Mingos, D. M. P., Nature Physical Science, 1972, 236, 99-102
- Kiremire, E. M., Orient. J. Chem., 2015, 31(1), 293-302.
- Kiremire, E.M., Orient. J. Chem., 2014, 30(4), 1475-1485.
- Kiremire, E. M. , ‘Beads, Necklaces, Chains and Strings in Capping Carbonyl Clusters’ submitted to Oriental, Journal of Chemistry.
- Cotton, F. A., Wilkinson, G., ‘Advanced Inorganic Chemistry’, 4th Edition, John Wiley & Sons, New York, 1980.
- Greenwood, N. N., Pure and Applied Chemistry, 1983, 55(9), 1415-1430.
- Lipscomb, W. N., Chemistry, 1976, 224-245.
- Hawthorne, M. F. , Pure and Applied Chemistry, 2003, 75, 1157-1164.
- Rudolph, R. W.,Accounts Chem. Res., 1976, 9(12), 446-452.
- Welch, A. J. Chem. Soc., Chem. Comm., 2013,49, 3615-3616.
- Kiremire, E. M. R., Kiremire, E. B. B., Materials Science Research India, 2007, 4(1), 09-18.
- Kiremire, E. M. R. Orient. J. Chem., 2007, 32(2), 809-812.

This work is licensed under a Creative Commons Attribution 4.0 International License.









