Batch, Kinetic and Equilibrium Studies of Chromium (Vi) From Aqueous Phase Using Activated Carbon Derived From Lantana Camara Fruit.

Introduction

Chromium as a toxic heavy metal often exists in the waste streams from various industries such as mining, tannery, metal cleaning, plating, dyeing and metal processing. According to the World Health Organization (WHO) drinking water guidelines, the maximum allowable limit for total chromium is only 0.05 mg/L. Hexavalent form is more toxic than trivalent and it requires more concern. Cr (VI) is found to be more toxic and highly soluble in water, whereas Cr (III) is less toxic and less soluble. Strong exposure to Cr (VI) causes cancer in digestive tract and lungs and may cause epigastric pain, nausea, vomiting, severe diarrhea and hemorrhage. Hence chromium removal from wastewater before disposal has become mandatory [1, 2].

The traditional physico-chemical processes used to eliminate heavy metals from the liquid effluents, such as chemical precipitation, ion exchange, and reverse osmosis treatments, are not usually viable from the economic and energy consumption point of view, especially when the concentrations of heavy metals are low [3].  Hence finding a suitable alternative treatment to overcome all these limitations is of great significance. Biosorption is one such low cost treatment which uses dead biomass for the removal of heavy metal pollutants from the aquatic environment[4]. This technique also shows better performance even at lower concentrations without the generation of any toxic byproducts.

Commercial activated carbon also has been widely used as one of the adsorbent in the treatment of heavy metals due to its exceptionally high surface areas, well-developed internal micro-porosity structure and wide spectrum of surface functional groups [5, 6]. But they exhibit higher efficiency only for specific metals and also found to be highly expensive .Hence there is a growing need to research also on extracting activated carbon from naturally available materials. There were several studies reported in the recent past on the development of low cost activated carbon derived from natural materials to remove heavy metals from aqueous solutions. However the problems associated with these adsorbents are the regeneration and recovery processes, which made them unattractive for wider commercial applications. This calls for a research effort to develop an industrially viable, cost effective and environmentally compatible technology for the removal of chromium from wastewater [7].

Lantana camara is a global weed which poses major threat to environment in and around Mudumalai Tiger reserve. Henceforth the biosorbent prepared from the fruit of this weed has been chosen to study the biosorption of hexavalent chromium. Preliminary studies showed better performance on activated carbon derived from Lantana camara fruit than the raw biosorbent and hence batch level experiments has been carried out using Lantana camara fruit derived activated carbon.

Material and Methods

Experimental Procedures

The batch mode biosorption studies were carried out from stock solution containing 1000 mg/L of Cr (VI) ions prepared using potassium dichromate salt. Sample solutions of desired concentrations (50 – 500 mg/L) were made from the prepared stock solution by series of dilutions. 50 ml volume of these solutions of various concentrations were collected in different Erlenmeyer flasks and was subjected to shaking with the required amount of adsorbent at a speed of 160 rpm until it reaches its equilibrium at a room temperature of 29⁰C.

The supernatant was filtered out using Whatman filter paper and a red violet coloured complex was obtained after the addition of 1,5-diphenylcarbazide to the acidified solution of known concentration. The prepared complex was analysed for chromium ions determination using UV-VIS spectrophotometer (Shimadzu) at a wavelength range of 540 nm. All the acidic range pH modifications were performed using 0.1N HCl in systronic digital pH meter. Throughout the experiment speed of agitation, volume of solution and temperature were maintained to be 160 rpm, 50 ml and 29⁰C respectively.

The un-adsorbed chromium ion was estimated by UV-VIS spectrophotometer and the equilibrium adsorption capacity of the adsorbent was determined according to the following equation:

 

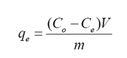
C_{o –} Initial metal ion concentration in mg/L, Ce_– equilibrium metal ion concentration in mg/L, q_e – adsorption capacity in mg/g,  m- mass of the bio-sorbent in grams, V – volume of the aqueous solution in litres.

The percentage removal of chromium was found using equation:

 

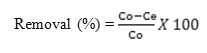
Adsorbent Preparation

Lantana camara fruit was collected from in and around Masinagudi ,Nilgris district, Tamilnadu, India. The fruits were washed several times with deionised water to remove dust and to remove any unwanted impurities followed by air drying. They were then powdered homogenously and treated with concentrated sulfuric acid in a ratio of 2:1. The powdered material were put in the muffle furnace in the presence of steam flow and carbonized at 300 ⁰ C for 9 hours.  Finally, they were sieved to obtain a uniform size of 150 µm and then stored in an air tight container for further use.

Batch Experiments and Process Parameters

Maximum adsorption capacity and adsorption efficiency were determined by conducting batch scale studies on varying initial chromium ion concentration, adsorbent dosage, pH and contact time.

Effect of Contact Time

To determine the equilibrium time, adsorption studies were carried out at different time intervals for several chromium ion concentrations ranging from 50 to 300 mg/L with an optimum dosage of 0.2 grams and a required pH of 1.

Effect of Initial Metal Ion Concentration

To study the effect of concentration on biosorption efficiency various chromium ion concentrations ranging from 50 to 500 mg/L were studied which was equilibrated for 75 minutes at an optimal pH of 1. The adsorbent dosage was maintained to be 0.2 grams for 50 ml of solution.

Effect of pH

The effect of pH on adsorption was studied for 50 mg/L chromium ion concentration solution with a biomass loading rate of 0.2 grams. As most of the literature supports acidic pH for favourable adsorption the study was done only for acidic range pH varying from 1 to 6 for a contact time of 75 minutes.

Effect of Adsorbent Dosage

The influence of biomass dosages on adsorption was investigated by varying the adsorbent doses from 0.05 to 0.45 grams at a pH of 1 for chromium ion concentrations 50, 150 and 300 mg/L respectively for a contact time of 75 minutes. Different chromium ions concentrations were studied to understand whether optimum dosage varies for different concentrations or remains the same.

Based on the results obtained optimized adsorption parameters were calculated and the influence of these factors in determining maximum metal uptake capacity was studied.

Isotherm and Kinetic Studies

Isotherm studies were performed to check the validity of Langmuir and Freundlich model for the given biosorbent and to determine maximum adsorption capacity. The chromium concentrations selected for this study range from 150 to 500 mg/L. The optimum pH of the solution was maintained to be 1 with an adsorbent dosage of 0.2 grams. To understand the rate of adsorption and to provide valuable insights on sorption mechanisms, kinetic studies were also performed using pseudo first-order and second-order models at 50, 100, 150, 200 and 250 mg/L chromium concentrations respectively. The optimum pH and adsorbent dosage was retained to be 1 and 0.2 grams respectively.

Result and Discussion

Effect of Initial Metal Ion Concentration

Based on the investigations on varying chromium concentrations between 50 – 500 mg/L the uptake capacity increased from 12.5 mg/g to 65 mg/g. The removal efficiency was found to be very higher reaching almost 99% at 50 mg/L as shown in figure 1. At lower concentrations, as more and more active binding sites are available, most of the chromium ions are adsorbed leading to higher removal efficiency. But at higher concentrations the efficiency was found to be only around 52%, which could be because of the presence of very fewer numbers of available sites for biosorption. As the metal ion/adsorbent ratio increases it results in the decrease of adsorption efficiency [8]. These findings indicate that the biomass is effective in dilute metal solutions and also the ratio of sorptive surface of the biomass to metal availability is high [9].  Based on these results the optimum concentration for further studies was fixed to be 50 mg/L.

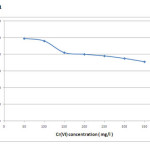Figure 1: Effect of initial metal ion concentration on adsorption efficiency  Click here to View figure

 

Effect of Contact Time and Concentration

The influence of contact time and its effect on the removal efficiency of chromium is as shown in figure 2. This study was performed at an optimum pH of 1 and the metal ion concentrations range from 50 – 300 mg/L at room temperature. The equilibrium time was determined to be 75 minutes with gradual increase in sorption capacity and removal efficiency for every five minutes. This equilibrium time is independent of initial metal ion concentration and hence it remains the same for all the concentrations studied. The equilibrium adsorption capacities were found to be 12.3, 24, 30.8, 40, 48.75 and 56.3 mg/g for concentrations 50, 100, 150, 200, 250 and 300 mg/L respectively. The uptake capacity is very rapid in the beginning and later exhibits slower rate of adsorption. The initial rapid phase may involve physical adsorption or ion exchange at cell surface and the subsequent slower phase may involve other mechanisms such as complexation, micro-precipitation or saturation of binding sites [10]. The later slow adsorption rate of the curve may also be due to the electrostatic hindrance caused by already adsorbed negatively charged adsorbate species and the slow pore diffusion of the ions [11, 12].   Hence an equilibrium time of 75 minutes has been chosen for carrying out further experiments.

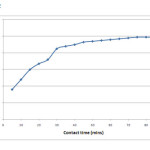Figure 2: Effect of contact time and concentration on adsorption efficiency  Click here to View figure

 

Effect of Adsorbent Dosage

The effect of adsorbent dosage, varying from 0.05 to 0.45 grams on chromium removal efficiency was investigated at a desirable pH of 1.  The doses of biosorbent were varied until 99% removal is obtained.  The study was carried out, at an equilibrium time of 75 minutes for chromium concentrations 50, 150 and 300 mg/L respectively. Figure 3 – depicts the increase in adsorption efficiency with increase in biomass dosage which later reaches saturation. The figure also shows that with increase in metal ion concentration, optimum dosage values also increases dramatically. Improved adsorption with an increase in biosorbent for each concentration of Cr (VI) is related to an increase in the ratio of adsorbent to adsorbate, which increases the surface area and the number of sites available for adsorption.  Saturation stage is attained because of the aggregation of solid particles at higher dosage levels of biomass which further reduces the surface area of the biosorbent [13, 14]. But the relationship between uptake capacity and biomass loading rates show a different trend, which decreases with increase in biosorbent dosage. This could be attributed to the fact that at high biosorbent dosages the available metal ions are insufficient to cover all the exchangeable sites on the biosorbent, usually resulting into low metal uptake [15, 16, 17]. The optimum dosage value obtained was not the same for all the concentrations studied. The optimum dosage of chromium concentrations 50, 150 and 300 mg/L were found to be 0.2 g, 0.25g, and 0.45 g respectively.

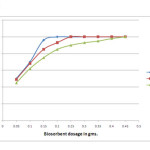Figure 3: Effect of adsorbent dosage on biosorption efficiency  Click here to View figure

 

Effect of pH of Solution

The study of influence of the pH is very significant in any batch studies on biosorption. Once necessary pH is achieved, biosorption shows a remarkable progress. The study on the effect of pH on biosorption efficiency was done at an equilibrium dosage of 0.2 grams at 50 mg/L initial chromium ion concentration. The pH of the solution was varied ranging from 1 to 6 for a contact time of 75 minutes. The adsorption advances at acidic ranges and maximum removal efficiency of up to 99% was obtained at a pH of 1 as shown in figure 4. At lower pH the biosorbent textures are positively charged and electrostatic force of attraction occurs with HCrO₄ ^–.  But at higher pH values, the biosorbent surface was negatively charged resulting in repulsive force between the biosorbent and CrO₄^2-, Cr₂O₇ ^2- [18, 19]. The decrease in percentage adsorption of chromium at higher pH also could be due to the high number of hydroxyl ions which causes hindrance to the diffusion of chromate ions [20]. Based on the results obtained, an optimum pH of 1 was chosen for carrying out rest of the experiments.

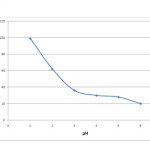Figure 4: Effect of pH of solution on adsorption efficiency  Click here to View figure

 

Adsorption Isotherm Models

Langmuir and Freundlich models were used to determine the relation between the equilibrium concentrations of the adsorbate in liquid phase and in the solid phase. The Langmuir isotherm model is valid for monolayer adsorption onto surface containing finite number of identical sorption sites and the Freundlich equation is applicable for sorption on heterogeneous surfaces.

Freundlich Adsorption Model

The Freundlich model habitually gives a better fit particularly for adsorption from liquids and can be expressed as:

 

In this model, the mechanism and the rate of adsorption are functions of the constants 1/n and K (L g−1). For a good adsorbent,0.2 < 1/n < 0.8, and a smaller value of 1/n indicates better adsorption and formation of rather strong bond between the adsorbate and adsorbent [21]. Based on the linear plot of log qe versus log Ce obtained from the experimental data as shown in figure 5, the Freundlich equilibrium constants were calculated.

Langmuir Adsorption Model

The Langmuir adsorption isotherm [22, 23] is given by the following equation:

 

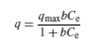
In this model, q_max (mg g−1) is the amount of adsorption corresponding to complete monolayer coverage, i.e., the maximum adsorption capacity and b (L mg−1) is the Langmuir constant. For Langmuir type adsorption process, to determine if the adsorption is favorable or not, a dimensionless separation factor is defined as [24]:

 

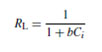
If R_L > 1, the isotherm is unfavorable, R_L = 1, the isotherm is linear, 0 < R_L < 1, the isotherm is favorable, R_L = 0, the isotherm is irreversible. The values of q_m and K_L can be determined from the linear plot of 1/q_e versus 1/C_e as shown in figure 6.

The results of Langmuir and Freundlich isotherms parameter are shown in table 1. Coefficient of determination values calculated from the adsorption isotherm studies confirms that the data fits well to Langmuir (R² = 0.97) isotherm than the Freundlich adsorption isotherm (R² = 0.85) representing monolayer adsorption. The R_L value 0.18 which lies between 0 and 1 show that the biosorbent selected for the present study exhibits favourable adsorption. The maximum monolayer adsorption capacity was found to be 86 mg/g which defines the total capacity of biosorbent in binding hexavalent chromium. A very low K_L value of 0.02151 L/mg represents the higher affinity for biosorption of chromium ions.

The Freundlich constants K_f and n were calculated from the plot and found to be 11.78 mg/g and 2.978 respectively. As 1/n value of 0.335 falls between 0.2 and 0.8, it indicates better adsorption potential and formation of rather strong bond between the adsorbate and adsorbent, which confirms that the selected biosorbent has more promising features in metal binding.

Table 1: Langmuir and Freundlich isotherm parameters

Parameters derived from Langmuir Isotherm	Parameters derived from Freundlich Isotherm
qm = 86 mg/gKL = 0.02151 L/mgR2 = 0.97	KF = 11.78 mg/gn= 2.978R2 = 0.85

 

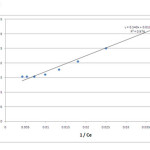Figure 5: Langmuir isotherm for Cr (VI) biosorption  Click here to View figure

 

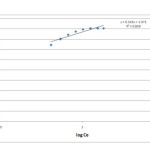Figure 6: Freundlich isotherm for Cr (VI) biosorption  Click here to View figure

 

Adsorption Kinetics

Pseudo-first-order and pseudo-second order models were used to check the validity of the experimental values. These models were tested at different concentrations and at various intervals of time. The uptake of heavy metal ions by seaweeds has often been observed to occur in two stages; an initial rapid uptake due to surface adsorption on cell walls and a subsequent slow uptake due to membrane transport of the metal ions on the cytoplasm of the cells[21]. Similar trend was obtained for the selected biosorbent with initial rapid sorption followed by slower rate of adsorption.

The following equation was used to check the validity of the pseudo-first-order model.

 

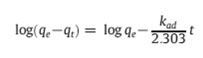
where q_t is the adsorption capacity at time t (mg/g) and k_ad (min⁻¹) is the rate constant of the pseudo-first order adsorption. The rate constant, k_ad and correlation coefficients of the Cr (VI) under different concentrations were calculated from the linear plots of log (q_e−q_t) versus time (figure 7).

The basic equation and the modified equation to obtain linearity are given below that check the applicability of the pseudo-second-order model which assumes to follow second order chemisorption

 

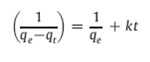
k is the rate constant of pseudo-second-order adsorption (g mg⁻¹ min⁻¹).

 

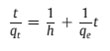
where h=kq_e² (mg g⁻¹ min⁻¹) can be regarded as the initial adsorption rate as t→0. The plot of t/q_t versus time (figure 8) should give a straight line if pseudo-second-order kinetics is applicable and q_e, k and h can be determined from the slope and intercept of the plot, respectively [25].

The result of pseudo first order and second order model is shown in table 2. Higher R² values were obtained for pseudo second order model than the first order model. The fitness of experimental data to a pseudo second order model implies that the adsorption is likely controlled by chemisorption [26] including the sharing or exchanging of ions between the metal ion and adsorbent.  Similar results were also reported in[27]. The model also supposes that that rate of occupation of adsorption sites is proportional to the squares of number of unoccupied sites [28].

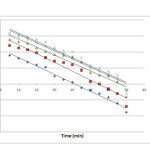Figure 7: Pseudo first-order kinetics at different Cr (VI) concentrations  Click here to View figure

 

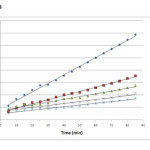Figure 8: Pseudo second-order kinetics at different Cr (VI) concentrations  Click here to View figure

 

Table 2: Kinetic and experimental values for pseudo first order model and second order model

Kinetic model	Parameters	Adsorbate Concentration
Pseudo-first-order model		50 (mg/L)	100(mg/L)	150(mg /L)	200(mg /L)	250(mg /L)
	kad (min−1)	0.06057	0.0638	0.0569	0.0589	0.0589
	qe,cal (mg/g)	12.23	32.09	44.38	64.09	70.42
	R2	0.98	0.95	0.94	0.94	0.96
Pseudo-second-order model	k (g mg−1 min−1)	0.0055	0.0018	0.00068	0.00038	0.00040
	qe,cal (mg/g)	14.45	29.67	44.44	62.89	71.9
	R2	0.99	0.99	0.98	0.97	0.96

 

Conclusions

The batch level experimental results obtained conclude that the selected biosorbent exhibit a very high metal uptake capacity of 86 mg/g with enhanced efficiency. This biosorbent shows a better performance even at very low concentrations of 50 mg/L with almost 99% removal.  Even at higher concentrations of 500 mg/L, 50% removal has been obtained with 0.2 grams of biosorbent which may be increased with higher dosages. Biosorption data showed a better fit with Langmuir isotherms, indicating the likelihood of monolayer sorption. The kinetics data best fitted to pseudo-second-order rate model than the pseudo first order kinetics which shows the involvement of chemical bonding in the binding mechanism of chromium. Hence batch studies on aqueous solution indicate that the selected biosorbent has a scope to remove hexavalent chromium from industrial wastewater for both higher and lower concentrations. Further work is planned to investigate on the applicability of this biosorbent in treating electroplating and tannery wastewater and scaling up of batch system to continuous mode operations.

References

1. Srividya, K.; Mohanty, K.; Chem. Eng. J. 2009, 155, 666-673.
2. Carmona, M. E. R.; da Silva, M. A. P.; Leite, S. G. F.; Echeverri, O. H. V.;  Ocampo-López, C.; J. Taiwan Inst. Chem. E. 2012, 43, 428-432
3. Bermúdez, Y. G.; Rico, I. L. R.; Guibal, E.; de Hoces, M. C.; Martín-Lara, M. Á.; Chem. Eng. J. 2012, 183, 68-76.
4. Volesky B., Biosorption of Heavy Metals, CRC Press, Inc. Florida, (1990)
5. Chingombe, P.; Saha, B.; Wakeman, R. J.; Carbon. 2005, 43, 3132-314
6. Yin, C. Y.; Aroua, M. K.; Daud, W. M. A. W.; Sep. Purif. Technol. 2007, 52, 403-415
7. Manjuladevi, M.; S. Manonmani.; Orient j. chem. 2015, 31, 531-539
8. Nordiana, J.; Dhir, B.; Kumar, R.; Int. J. Environ. Res. 2013, 4, 427-432
9. Santuraki, A. H.; Barminas, J. T.; IJSTR. 2015, 5, 1-8
10. Gupta, V. K.; Rastogi, A. J.; Hazard Mater. 2009, 163, 396-402
11. Goswami, S.; Ghosh, U. C.; Water SA. 2006, 31, 597-602
12. Pandey, P. K.; Sharma, S. K.; Sambi, S. S.; Int. J. Environ. Sci. Tech. 2010, 7, 395-404
13. Bansal, M.; Singh, D.; Garg, V. K.; .J. Hazard Mater. 2009, 171, 83-92
14. Moussavi, G.; Barikbin, B.; Chem. Eng. J. 2010, 162, 893-900
15. Vijayaraghavan, K.; Palanivelu, K.; Velan, M.; Bioresource Technol.2006, 97, 1411-1419
16. Fourest, E.; Roux, J. C.; Appl. Microbiol. Biot.1992, 37, 399-403
17. Babalola, J. O.; Babarinde, N. A. A.; Oninla, V. O.; Popoola, O. A.; PJST. 2008, 9, 610-620
18. Rangabhashiyam, S.; Selvaraju, N.; J. Taiwan Inst. Chem. E.  2015, 47, 59-70
19. Kapur, M.; Mondal, M. K.; Chem. Eng. J. 2013, 218, 138-146
20. Olayinka, K. O.; Alo, B. I.; Adu, T.; J. Appl. Sci. 2007, 7, 2307-2313
21. Basha, S.; Murthy, Z. V. P.; Jha, B.; Chem. Eng. J. 2008, 137, 480-488
22. Langmuir, I.; J. Am. Chem. Soc. 1916, 38, 2221-2295
23. Langmuir, I.; J. Am. Chem. Soc. 1917, 39, 1848-1906
24. Hall, K. R.; Eagleton, L. C.; Acrivos, A.; Vermeulen, T.; Ind. Eng. Chem. Fund. 1966, 5, 212-223
25. SenthilKumar, P.; Ramalingam, S.; Sathyaselvabala, V.; Kirupha, S. D.; Sivanesan, S.; Desalination. 2011, 266, 63-71
26. Wang, X. S.; Chen, L. F.; Li, F. Y.; Chen, K. L.; Wan, W. Y.; Tang, Y. J.; J. Hazard Mater. 2010, 175, 816-822
27. Sarı, A.; Tuzen, M.; J. Hazard Mater. 2008, 160, 349-355
28. Karthikeyan, S.; Balasubramanian, R.; Iyer, C. S. P.; Bioresource Technol. 2007, 98, 452-455

---

This work is licensed under a Creative Commons Attribution 4.0 International License.