DFT investigation of Li⁺complexation of novel boron nitride 12-crown-4 ethers: Gas, Water and Benzene phases study

Introduction

Macrocyclicpolyethers or crown ethers have an interesting property to accommodate selectively many different ions into their cavities to form stable complexes. They originally prepared by Pedersenat Du Pont in 1967[1]. Since that the field of molecular recognition has received aconsiderable amount of interest[2-6].Crown ethers have been proposed as separation agents for removing metal like Cs⁺ and Sr²⁺ from mixed nuclear and chemical wastes[7-9]. They also found widespread applications many areas of science [10-14]. Due to this fact that crown ethers may be imagined as the simplest representatives of enzymes in the interaction with cations, computational chemists are also interested in them. Theoretical investigations has been a powerful method to clarify the mechanism of selective capture and transportation of metal ionsby crown ethers and their derivatives[15-18]. At present, for their pre-organized geometries, crown ethers are a favorite molecular platform for architecting novel receptors[19]. The scope of molecular recognition is currently inquired about highly diversified structural component[20]. It is worth mentioning that due to their generally good solubility requirement in a variety solvents,simple crown ethers are still noteworthy materials to investigate. Liu and co-workers synthesized novel crown ether porphyrin[21]. The porphyrinappended with four crown ether units at meso-positions via an acetylene bridge. They demonstrated that the novel structure makes stable complex with Cs⁺and K⁺. In a theoretical investigation by DFT, the complexes of 12-Crown-4 and its heterocyclic derivatives containing N, P, and S atoms with Be²⁺ studied [22]. They applied B3LYP functional with 6-31+G** basis set to perform the calculations. The results verified aza-12-crown-4 as the host with highest metal binding selectivity. Armentrout and his research group conducted a study on interactions of alkali metal cations with 12-Crown-4[23]. In the computational part they used B3LYP and MP2(full) levels of theory with HW*/6-311+G(2d,2p) and def2-TZVPPD basis sets. They studied relative energies, and BEDs of complexes of Na⁺, K⁺, Rb⁺, and Cs⁺ with 12C4 crown ether.In the present paper,for the first time we have performed a density functional theory investigation on 12C4 and six novel boron nitride 12C4 crown ethers with Li⁺with the Gaussian 98 program[24]. The study carried out in water and benzene phases besides gas phase. We obtain the binding energies, and various thermodynamic parameters of free ligands, and complexes. The stability constants and partition constants of all complexes in water and benzene phases studied by polarized continuum model, IEF-PCM. The NBO analysis carried out on all complexes to obtain the efficient donor-acceptor molecular orbitals in the Li-complexes.

Computational Details

B3LYP hybrid functional of density functional theory [25]was applied to optimize the geometries of free ligands, and their complexes. The mentioned functional has been used for Hessian calculations to analyze frequencies, solvation studies, and NBO calculations as well. To model molecular orbitals of structures all electron correlated 6-311+G(d,p) basis set[26] has been used. It is a standard valence triple zeta basis set augmented with diffuse functions. The diffuse functions are present to describe barely bound electrons in complexes. Calculations were performed without imposing any symmetry restriction during geometry optimizations.

The true stationary structures were tested by the absence of any imaginary vibrational frequency through hessian calculations. Hessian calculations were also used for the estimation of various thermodynamic parameters at temperature of 298.15 K and pressure of 1.00 atm.

Inaddition, the natural bond orbital (NBO) analysis [27] were calculated for all the stable structures of all crown ethers binding with Li⁺. The NBO calculations performed using NBO 3.1 program as implemented in the Gaussian 98 package [24]at the DFT/B3LYP level with 6-311++G(d,p) [26] large basis set to understand various second-order interactions between the filled molecular orbitals of one subsystem and vacant molecular orbitals of another subsystem,which is a measure of the delocalization or hyper conjugation[28].

To model the structures in water and benzene solutions we chose a specific continuum model called the integral equation formalism polarizable continuum model (IEF-PCM).This model presents good accuracy, reliability, adaptability,and a reduced computational effort in describing solvent effects [29-33]. All calculations were performed with Gaussian 98 suite of programs [24].

Results and Discussions

The novel boron nitride 12C4 crown ethers (Figs. 1-7) were chosen from a previous work on novel BN 12C4 crown ethers [34]. We picked the BN 12C4 ethers with equal number of boron and nitrogen atoms to increase the chance of finding some non-polar novel BN crown ethers like 12C4. The candidates were selected among those structural isomers with the most favorable total electronic energy and/or with a molecular dipole moment of zero (like 12C4).

We have performed geometry optimizations of 12C4, all free boron nitride crown ethers and their Li⁺ complexes (Figs. 1-7) at the B3LYP [25] level of theory along with 6-311+G(d,p) standard basis set [26]. Symmetries of optimized structures, the number of imaginary frequencies, total electronic energies including zero-point energies, and molecular dipole moments of free crown ethers and their complexes with lithium cation in water and benzene phases are presented in Table 1.

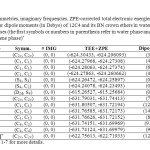Table1: Symmetries, imaginary frequencies, ZPE-corrected total electronic energies (in Hartree) and molecular dipole moments (in Debye) of 12C4 and its BN crown ethers in water and benzene phases (the first symbols or numbers in parenthesis refer in water phase and the seconds refer to benzene phase)*  Click here to View table

 

For the symmetries we applied the approximate higher-order point groups with cutoff level of 0.1 to make the probable structural changes of the crown ethers sensible in water and benzene. As Table 1 shows, with the mentioned criterion among free ligands only isomer 6 and 12C4 have different symmetries in water and benzene phases. The observation for the crown ether complexes is different. In this set only [5…Li]⁺ complex has the different point groups in water (C₄) and benzene phases (C₂). According to the symmetries in Table 1 and based on the explained symmetry criterion 12C4 shows D_2d and S₄ symmetries in water and benzene phases, respectively.

The Table also shows that the calculated vibration frequencies of the complexes are all positive. It means there are no imaginary frequencies for relaxed geometries indicating that these complexes were located at the minima points of the potential energy surfaces. For all structures, total electronic energies in water solution are more favorable than those benzene solution (Table 1) even for non-polar structures. The observation might be explained based on lone pair of electrons of oxygen atoms which make energetically favorable interactions with polar molecules of water phase. Total electronic energies in water phase is more favorable that benzene phase in all crown ethers and their complexes.

Among free ligands, isomer 4 has the largest electronic energy difference (11.3 kcal/mol) while for the Li⁺-complexes, [2…Li]⁺ shows the largest electronic energy difference (52.2 kcal/mol). In general water-benzene electronic energy differences for Li⁺-complexes are much larger than free ligands.

The overall trend in dipole moments (Table 1) of studied crown ethers and their complexes in water and benzene phases were the same, as well. It means the molecular dipole moments of the crown ethers were larger in water than benzene. However, there were structures like [4…Li]⁺ and [5…Li]⁺ that the dipole moments in water were smaller than that of in benzene. The Table also reveals that isomers 5 and 6 of BN 12C4 crown ethers have non-polar geometries like 12C4 in both water and benzene solutions. The dipole moment of the most polar complex, [3…Li]⁺ (14.2 D) did not undergo change in  water or benzene phase.

Structural analysis of crown ethers and their complexes with Li⁺

The optimized structures of 12C4, six BN 12C4 crown ethers, and all Li⁺-complexes are shown in Figs. 1-7. The NBO analysis showed that unlike 12C4 crown ether which has no double bonds, all BN 12C4 crown ethers have fourπ bonds. The location of these double bonds in BN crown ethers, and their complexes were the same. So we displayed them only on Li⁺-complexes of crown ethers. In all BN 12C4 crown ethers and their Li⁺-complexes there were four boronnitride double bonds as presented in Figures 1-4. The exceptions are isomers 3 and 4 which have an additional B-O double bond in their free structures. These double bonds are shown on Figures 4 and 5 on the related free crown ethers structures. The B-O double bonds did not stand in their Li⁺-complexes. The results showed that binding Li⁺ with BN 12C4 ligands did not affect the BN double bonds. However, in the BN 12C4 structures which showed B-O double bonds, the B-O π bond opened in favor of binding the oxygen atom with Li cation.

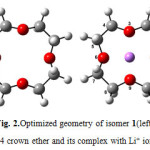Figure1: Optimized geometry of 12C4crown ether (left) and its complex with Li+ ion (right)  Click here to View figure

 

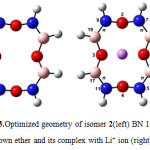Figure2: Optimized geometry of isomer 1(left) BN 12C4 crown ether and its complex with Li+ ion (right)  Click here to View figure

 

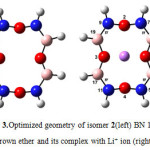Figure3: Optimized geometry of isomer 2(left) BN 12C4 crown ether and its complex with Li+ ion (right)  Click here to View figure

 

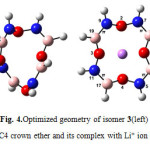Figure4: Optimized geometry of isomer 3(left) BN 12C4 crown ether and its complex with Li+ ion (right)  Click here to View figure

 

Table 2 collects the most important geometrical parameters of free crown ether ligands and their complexes with Li⁺ in water, and benzene phases. According to the geometric parameters of 12C4 (Fig. 1) listed in Table 2, the bond lengths (C-O and C-C) of the free ligand did not undergo significant changes after binding oxygen atoms of ligand with Li⁺. The trend is the same for both water and benzene phases. On the other hand, the marked changes in geometrical characteristics appeared in bond angles which observed more considerable than bond lengths (Table 2). It means interaction of 12C4 with Li⁺clearly reflects on bond angles of its structure.

Table2: Significant bond lengths and nonbonding distances (in angstroms, Å) andbonding angles (in degrees, °) of 12C4 and its BN crown ethers and their Li+-complexes in water and benzene phases*  Click here to View table

 

The mention trends for bond lengths, and angles as we discussed above, generally followed in the novel BN 12C4 crown ether and their complexes. The bond lengths did not change significantly in BN 12C4 crown ethers but in isomers 3 and 4 (Figs. 4 and 5) B-O π bond opened after interaction of the BN crown ether with Li⁺(as we discussed earlier). This was the only dramatic change in chemical bond frame of isomers 3 and 4 complexes.

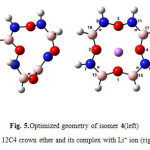Figure5: Optimized geometry of isomer 4(left) BN 12C4 crown ether and its complex with Li+ ion (right)  Click here to View figure

 

At first glance one can find that all structures of BN crown ethers turn to a nearly flat geometry after binding with Li⁺(Figs. 1-7). Considering chemical bonds and angles in Table 2 reveals the mentioned geometrical changes were due to changes in bond angles. The Table also shows that the largest changes of bond angles of BN crown ethers occurs in isomer 5 (Fig. 6) with average changes in bond angles of about 9° in water (and also in benzene). The smallest changes of bond angles belongs to isomers 3(with average changes of about -0.3° in water) (Fig. 4) and 6 (with average changes of about 0.6° in benzene) (Fig. 7).

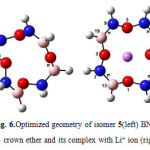Figure6: Optimized geometry of isomer 5(left) BN 12C4 crown ether and its complex with Li+ ion (right)  Click here to View figure

 

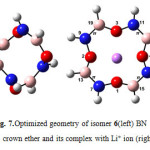Figure7: Optimized geometry of isomer 6(left) BN 12C4 crown ether and its complex with Li+ ion (right)  Click here to View figure

 

Another important geometric parameters of the crown ethers complexes are the distances between oxygen donor atoms and lithium ion. As Table shows O…Li distances are in the range of 1.94-2.62 Å. The Table also shows that O…Li distances are slightly shorter in benzene solutions than water solutions for all crown ether complexes. While the O…Li distances of novel BN 12C4 crown ethers present slight difference from those of 12C4; the O…Li…O angles were more different (Table 2).  As Table shows there are no steady trend comparing these angles in BN 12C4 crown ether complexes with 12C4. The only general observation is that O…Li…O angles were smaller in water phase than benzene in all cases, and the differences is considerable. This means in benzene solution the cation displays an increased tendency to be pulled toward the cavity of crown ethers.

Second-order interaction energies from NBO calculations

One of the ways to elucidate the different selectivity of crown ethers towards a metal ion, is NBO analysis. In NBO analysis, the values of stabilization energies (the second-order interaction energies E_ij⁽²⁾) are closely related to the strength of binding interactions. A complex will generally be more stable if it has larger corresponding stabilization energy E_ij⁽²⁾.

We gathered the four most efficient donor-acceptor stabilization energies in Table 3. These interactions selected from the interactions of donor molecular orbital of the crown ethers with lithium cation acceptor molecular orbitals. As it is clear from Table 3 in 12C4 and all BN 12C4 the first four efficient donor molecular orbitals are lone pairs/pairs of oxygen atoms. The exceptions are complexes of isomers2 and 4 (Figs. 3 and 5). In these two BN 12C4 crown ether complexes one σ(BO) molecular orbital acts as a donor molecular orbital to interact with unoccupied molecular orbital of Li⁺. The NBO analysis showed that nitrogen atoms in novel BN 12C4 crown ether complexes are not able to interact with acceptor molecular orbitals of Li⁺ because the lone pairs of all nitrogen atoms are totally engaged in π chemical bonds.

Table3: Selected stabilization interaction E2 (kcal/mol) of 12C4 and BN 12C4 crown ethers complexes with Li+cation in water and benzene phases*  Click here to View table

 

According to the energy of interactions of crown ethers with Li⁺(Table 3) the average stabilization energies in benzene phase are larger than that of in water. It might be related to the unfavorable interaction between polar Li⁺ and/or studied crown ethers, and non-polar benzene molecules. The differences are in the range of 2.3-3.7 kcal/mol. The smallest differences refers to the structures with a molecular dipole moment equal to zero namely 12C4, isomers 5complex (Fig. 6) and 6 complex(Fig. 7).

Based on interaction between Lewis-type NBOs (donor) and non-Lewis NBOs (acceptor) 12C4 with the largest average stabilization energies (15.1 kcal/mol in water and 17.8 kcal/mol in benzene) shows the best selectivity for lithium cation. Following the same reasoning, among the novel BN 12C4 crown ethers, isomer 6 complex (Fig. 7) with the largest average stabilization energy (8.2 kcal/mol in water and 10.5 kcal/mol in benzene) shows the best selectivity for Li⁺ in comparison with the other BN 12C4 crown ethers.

Binding Energies

The most important property for metal cations selectivity with crown ether is the binding energy (ΔE_ele). Binding energy also is a simple way to predict the strength of interaction between host–guest species. The selectivity of 12C4 and novel BN 12C4 crown ethers for Li⁺complexation have been studied in gas phase (Figs. 1-7). The calculated binding energies, enthalpies and Gibbs free energies of M⁺/L complexes, based on the reaction (1).

Ligand + Li⁺ → Complex   (1)

The binding energy of Li⁺-ether complex is defined by the following general relation:

ΔE_ele = E_ele(Complex)→E_ele(Li⁺) + E_ele(Ligand)     (2)

The binding energy in the mentioned form is D_e. It is clear that D₀ is true binding energy due to the principle that all molecules have vibrations even at zero absolute temperature. Therefore, we added zero-point vibrational energy to ΔE_ele in order to improve the binding energy.

The calculated binding energies, binding enthalpies and Gibbs free energies are given in Table 4. As is comes from Table 4, among BN 12C4 crown ethers isomer 6 and 5complexes with the most negative ΔE_ele of -88.23 and -86.44 kcal/mol predicted to form the most stable complexes with Li⁺ in gas phase. Based on the same criterion the complex of isomer 4(Fig. 5) with lithium cation appeared to be the most unstable one. It is clear that one cannot compare the stability of 12C4 complex with any BN 12C4 crown ethers based on ΔE_ele of complexation reaction due to different types of atoms available in 12C4 and BN 12C4 crown ethers.

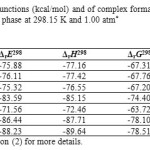Table4: Thermodynamic functions (kcal/mol) and of complex formation between Li+ and studied crown ethers in gas phase at 298.15 K and 1.00 atm*  Click here to View table

 

Calculated values of thermodynamic parameters binding enthalpy, free energy of complexation and entropy of complexation (ΔS) are also listed in Tables 4. These thermodynamic functions provide information about the relative stability of studied crown ether complexes as well. Formation of lithium ion complexes is exothermic according to the values of ΔH given in Table 4. As Table shows isomer 6 (Fig. 7) of BN 12C4 crown ether with a change of enthalpy of -89.64 kcal/mol (which is much more favorable than 12C4) had the best value for complexation with Li⁺ among studied crown ethers. The calculations also predicted isomers 5(Fig. 6) and 3(Fig. 4) better choices for binding with Li⁺ than 12C4 due to more negative change of enthalpy of complexation. The entropy change for the complexation reaction was slightly negative. However, entropy in complex formation is low, and enthalpy changes are effective driving forces for complex formation. From the Gibbs free energy of complexation it is found that Li⁺–crown ether complexes were spontaneously formed and stable.

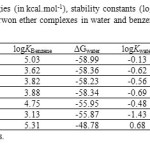Table5: Solvation free energies (in kcal.mol-1), stability constants (logK), and partition constants (logP) of studied crwon ether complexes in water and benzene at 298.15 K and 1.00 atm*  Click here to View table

 

Prediction of stability and partition constants in water and Benzene

In order to calculate the stability constants of complexes, Gibbs free energy of reactants (crown ethers and Li⁺) and product ([Li…ether]⁺ complex) in solution phases (benzene and water) are needed. The Gibbs free energy solution-phase can be calculated by connecting gas-phase Gibbs free energy and solvation free energy by a simple thermodynamic cycle which is known as Born–Haber cycle (Fig. 8). The thermodynamic cycle method is the most significant and extensively used simulation method [6].In this paper, solvation free energies of chemical species in reaction (2) are predicted by IEF-PCM model [29-33]. Table 5 collects solvation free energies in water and benzene phases, stability constants and partition constants of complexes using thermodynamic cycle of Fig. 8.

Figure8: Simple thermodynamiccycle to link gas-phase free energy to solution-phase free energy  Click here to View figure

 

As Table 5 shows, solvation free energies in benzene for 12C4 is -29.57 kcal/mol. The negative value of ΔG_benzene predicts solvation process of 12C4 spontaneous at 1.00 atm and 298.15 K. This is true for all novel BN 12C4 crown ethers (Figs. 1-7) as well. They all have negative changes of free energies of solvation in benzene. Among BN crown ethers, isomer 2 (Fig. 3) with a ΔG_benzene of -31.14 kcal/mol has the largest negative change of free energy for solvation in benzene phase. Comparing ΔG_benzene and ΔG_watervalues in Table 5 shows that all solvations of the crown ether complexes in water are also spontaneous. The values of ΔG_water is more negative for all ethers than ΔG_benzene. It might be interpreted based on high electric dipole moments of [Li…ether]⁺ complexes (see Table 1 for molecular dipole moments).

The stability constants in benzene shows that isomer 6 complex(Fig. 7) has the largest stability constant in benzene. Evaluating the stability constants in water reveals that only isomer 6 complex has positive stability constant like that of in benzene. This makes [Li…6]⁺ complex (Fig. 7) the most stable complex among all studied crown ethers in water. The negative signs of logK in water for 12C4 and isomers 1 to 5 (Figs. 2-6) interpret the unstable nature of these crown ethers with Li⁺ in water phase. The most unstable complex is [Li…5]⁺ (Fig. 6) with a logK of -1.43 based on this criterion.

Figure 9  Click here to View figure

 

The partition constants in Table 5 clearly reflect the difference in solubility of studied crown ether complexes in benzene and water phases. As Table shows the complex of isomer 4(Fig. 5) among BN 12C4 crown ethers with a partition constant of 26.01 has the largest value of the quantity. This partition constant is close to that of 12C4 crown ether (25.64). This might be an evident of better distribution of isomer 4 complex (Fig. 5) in comparison with 12C4 complex when two phases are benzene and water. The other BN 12C4 crown ether isomers all have smaller partition constants than 12C4 for benzene/water immiscible phases.

Conclusions

DFT study of selected novel boron nitride 12C4 crown ethers with Li⁺have been studied in the gas, benzene and water phases. The results of B3LYP and IEF-PCM calculations contained useful clues for extraction of lithium cation between benzene/water phases. Evaluations showed that with applying approximate higher-order point groups to crown ethers 12C4 and isomer 6 and [5…Li]⁺ possess different symmetries in water and benzene phases. The optimized geometries of all novel BN crown ethers refer to minima points of the potential energy surfaces due to lack of imaginary frequencies in water and benzene.

Total electronic energies in water phase are more favorable than those benzene solution for studied crown ethers and their complexes even for non-polar structures. In general, the molecular dipole moments of the crown ethers were larger in water than benzene phase (the exceptions are [4…Li]⁺ and [5…Li]⁺). The non-polar structures, isomers 5 and 6 of BN 12C4 crown ethers have electric dipole moment of zero in both water and benzene phases. The most polar structure do not show change of its dipole moment in water and benzene.

All studied BN 12C4 crown ethers have four BN π bonds. Isomers 3 and 4 have one more BO π bond which vanishes after binding these isomers with Li⁺. However, BN π bonds remain intact in all crown ethers. The significant structural changes occurs in bond angles and all structures of BN crown ethers turn to a nearly flat geometry after binding with Li⁺.

The O…Li distances are slightly shorter in benzene solutions than water solutions for all crown ether cpmplexes. The O…Li…O angles in crown ether complexes were smaller in water phase than with a considerable value. This means in benzene solution the cation displays an increased tendency to be pulled toward the cavity of crown ethers.

NBO analysis of efficient donor-acceptor stabilization energies show that the first four efficient donor molecular orbitals are lone pairs/pairs of oxygen atoms except for isomers 2 and 4. In these two BN 12C4 crown ethers a σ(BO) molecular orbital is among the four efficient donor molecular orbitals. The NBO analysis also shows that the average stabilization energies in benzene phase are larger than that of in water.

Based on interaction between donor NBOs and acceptor NBOs after 12C4, isomer 6 among the novel BN 12C4 crown ethers with the largest average stabilization energy shows the best selectivity for Li⁺ both in water and benzene.

The calculated binding energies show that isomer 6 and 5 with the most negative change of electronic energies form the most stable complexes with Li⁺in gas phase. Formations of lithium ion complexes are exothermic and spontaneous in gas phase. The most exothermic complexation belongs to isomer 6. Based on negative change of enthalpy of complexation isomers 5 and 3 are better choices for binding with Li⁺ than 12C4 in gas phase.

The IEF-PCM predictions in solution phases show spontaneous solvation processes for 12C4 and all BN 12C4 crown ethers at 1.00 atm and 298.15 K. All solvation processes of the crown ethers are also spontaneous in water. The values of ΔG_water is more negative for all ether complexes than ΔG_benzene showing greater tendencies of the complexes to be solved in water due to their high molecular electric dipole moments. Isomer 6 complex has the largest stability constant in benzene and is the one that has positive stability constant in benzene. Based this observation, [Li…6]⁺ complex is the most stable complex among all studied BN crown ether complexes in water. The negative signs of stability constants in water for complexes of 12C4 and isomers 1 to 5 interpret the unstable nature of these crown ethers with lithium cation in water phase. The most unstable complex is isomer 5 based on calculated stability constant criterion in water.

The calculated partition constants show that complex of isomer 4 with Li⁺has the largest value of partition constant. This observation makes isomer 4 complex with a better distribution than 12C4 between two benzene and water phases. As results show the other BN 12C4 crown ether isomers all have smaller partition constants than 12C4 for benzene/water immiscible phases.

Acknowledgments

This work was funded by Islamic Azad University,Boroujerd branch. The authors also gratefully acknowledge the computing time provided bythe Iranian High Performance Computing Center(http://www.iranhpc.com/) for performing all the research computations.

References

1. Pedersen, C. J. J. Am. Chem. Soc.1967, 89, 7017-7036.
2. Cram, D. J. Angew. Chem. Int. Ed.1988, 27, 1009-1020.
3. Cram, D. J. Angew. Chem. Int. Ed.1986, 25, 1039-1057.
4. Cram, D. J.; Katz, H. E. J. Am. Chem. Soc.1983, 105, 135-137.
5. Lybrand, T. P.; McCammon, J. A.; Wipff, G. Proceedings of the National Academy of Sciences1986, 83, 833-835.
6. Tembre, B. L.; Mc Cammon, J. A. Comput. Chem.1984, 8, 281-283.
7. Schulz, W.; Bray, L. Sep. Sci. Technol.1987, 22, 191-214.
8. Moyer, B. A.; Birdwell Jr, J. F.; Bonnesen, P. V.; Delmau, L. H. In Macrocyclic Chemistry; Springer, 2005, p 383-405.
9. Horwitz, E. P.; Dietz, M. L.; Fisher, D. E. Solvent Extr. Ion Exch.1991, 9, 1-25.
10. Kozak, R. W.; Waldmann, T. A.; Atcher, R. W.; Gansow, O. A. Trends Biotechnol.1986, 4, 259-264.
11. Chiarizia, R.; Horwitz, E.; Dietz, M. Solvent Extr. Ion Exch.1992, 10, 337-361.
12. Bourgoin, M.; Wong, K.; Hui, J.; Smid, J. J. Am. Chem. Soc.1975, 97, 3462-3467.
13. Macdonald, C. L.; Bandyopadhyay, R.; Cooper, B. F.; Friedl, W. W.; Rossini, A. J.; Schurko, R. W.; Eichhorn, S. H.; Herber, R. H. J. Am. Chem. Soc.2012, 134, 4332-4345.
14. Dubonosov, A. D.; Minkin, V. I.; Bren, V. A.; Shepelenko, E. N.; Tsukanov, A. V.; Starikov, A. G.; Borodkin, G. S. Tetrahedron2008, 64, 3160-3167.
15. Bultinck, P.; Goeminne, A.; Van de Vondel, D. THEOCHEM1999, 467, 211-222.
16. Hill, S. E.; Feller, D. Int. J. Mass spectrom.2000, 201, 41-58.
17. Bagatur’yants, A.; Freidzon, A. Y.; Alfimov, M.; Baerends, E.; Howard, J.; Kuz’mina, L. THEOCHEM2002, 588, 55-69.
18. Okano, K.; Tsukube, H.; Hori, K. Tetrahedron2004, 60, 10877-10882.
19. Sukwattanasinitt, M.; Rojanathanes, R.; Tuntulani, T.; Sritana-Anant, Y.; Ruangpornvisuti, V. Tetrahedron Lett.2001, 42, 5291-5293.
20. Lehn, J. M. Angew. Chem. Int. Ed.1990, 29, 1304-1319.
21. Liu, Y.-C.; Kuo, M.-C.; Lee, C.-W.; Liang, Y.-R.; Lee, G.-H.; Peng, S.-M.; Yeh, C.-Y. Tetrahedron Lett.2008, 49, 7223-7226.
22. Diao, K.-S.; Wang, H.-J.; Qiu, Z.-M. THEOCHEM2009, 901, 157-162.
23. Armentrout, P.; Austin, C.; Rodgers, M. Int. J. Mass spectrom.2012, 330, 16-26.
24. Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb, M. A.; Cheeseman, J. R.; Zakrzewski, V. G.; Montgomery, J. A. J.; Stratmann, R. E.; Burant, J. C.; Dapprich, S.; Millam, J. M.; Daniels, A. D.; Kudin, K. N.; Strain, M. C.; Farkas, O.; Tomasi, J.; Barone, V.; Cossi, M.; Cammi, R.; Mennucci, B.; Pomelli, C.; Adamo, C.; Clifford, S.; Ochterski, J.; Petersson, G. A.; Ayala, P. Y.; Cui, Q.; Morokuma, K.; Malick, D. K.; Rabuck, A. D.; Raghavachari, K.; Foresman, J. B.; Cioslowski, J.; Ortiz, J. V.; Baboul, A. G.; Stefanov, B. B.; Liu, G.; Liashenko, A.; Piskorz, P.; Komaromi, I.; Gomperts, R.; Martin, R. L.; Fox, D. J.; Keith, T.; Al-Laham, M.; Peng, C. Y.; Nanayakkara, A.; Gonzalez, C.; Challacombe, M.; Gill, P. M. W.; Johnson, B.; Chen, W.; Wong, M. W.; Andres, J. L.; Gonzalez, C.; Head-Gordon, M.; Replogle, E. S.; Pople, J. A. Gaussian 98, revision A.7. ; Gaussian, Inc.: Pittsburgh, PA, 1998.
25. Becke, A. D. J. Chem. Phys.1993, 98, 5648-5652.
26. Krishnan, R.; Binkley, J. S.; Seeger, R.; Pople, J. A. The J. Chem. Phys.1980, 72, 650-654.
27. Reed, A. E.; Curtiss, L. A.; Weinhold, F. Chem. Rev.1988, 88, 899-926.
28. Chocholoušová, J.; Špirko, V.; Hobza, P. Phys. Chem. Chem. Phys.2004, 6, 37-41.
29. Miertuš, S.; Scrocco, E.; Tomasi, J. Chem. phys.1981, 55, 117-129.
30. Miertus, S.; Tomasi, J. Chem. phys.1982, 65, 239-245.
31. Pascual‐Ahuir, J.; Silla, E.; Tomasi, J.; Bonaccorsi, R. J. Comput. Chem.1987, 8, 778-787.
32. Cances, E.; Mennucci, B.; Tomasi, J. J. Chem. Phys.1997, 107, 3032-3041.
33. Cancès, E.; Mennucci, B. J. Math. Chem.1998, 23, 309-326.
34. Zeighami, N.; Boshra, A.; Oliaey, A. R. J. Phys. Theor. Chem.2014 10, 171-187

 

 

---

This work is licensed under a Creative Commons Attribution 4.0 International License.