Classification of Transition Metal Carbonyl Clusters Using the 14n Rule Derived from Number Theory

1

Classification of Transition Metal Carbonyl Clusters Using the 14n Rule Derived from Number Theory

Volume 31, Number 2

Enos Masheija Kiremire

Department of Chemistry and Biochemistry, University of Namibia, Private Bag 13301, Windhoek, Namibia

kiremire15@yahoo.com

DOI : http://dx.doi.org/10.13005/ojc/310201

Article Publishing History
Article Received on :
Article Accepted on :
Article Published : 09 Jun 2015

Article Metrics

ABSTRACT:

This paper introduces a method of classifying clusters of the transition metal carbonyls and main group elements based on the 14n and 4n rules. The two rules are interrelated. They were derived from close analysis of the relationship between the number of skeletal atoms, valence electrons and eighteen electron rule in the case of transition elements, and octet rule for main group elements and the known bonds or linkages of simple clusters. The analysis reveals that there is an infinite range of carbonyl clusters some of which are yet to be discovered. These clusters occur in an orderly manner in of clusters pertaining to definite series. In addition to the categorization of clusters, tentative structures of some clusters especially the simple ones can be predicted. Furthermore, the method can identify the INNER CORE NUCLEAR CLUSTER of some large carbonyl clusters. The method is simple and enjoyable to use.

KEYWORDS:

Classification; Transition; Derived

Download this article as:

Copy the following to cite this article:

Kiremire E. M. Classification of Transition Metal Carbonyl Clusters Using the 14n Rule Derived from Number Theory. Orient J Chem 2015;31(2).

Copy the following to cite this URL:

Kiremire E. M. Classification of Transition Metal Carbonyl Clusters Using the 14n Rule Derived from Number Theory. Available from: http://www.orientjchem.org/?p=9151

Introduction

Transition metal carbonyl clusters have stimulated immense interest for several decades largely due to their vast and intriguing structural architecture,numerous potential industrial applications and challenging bonding properties.In this regard, the work by Wade and Mingos^1-2as well as Jemmis^3-4has contributed tremendously towards understanding of clusters. Subsequently, other research groups such as those headed by King, Teo,Zanello, and Slovokhotov^5-9have expanded the knowledge especially on the large carbonyl clusters. The polyhedral skeletal electron pair theory (PSEPT) which uses mainly the 4n, 5n and 6n rules has classified clusters as closo, nido, arachno, hypho and some klapo¹⁰. However on closer scrutiny of the structures and formulas of the simple boranes, hydrocarbons, carboranes and transition metal carbonyl clusters reveals that these clusters both simple and complex ones belong to a wide range of an infinite series. The series are formed according to definite numerical sequences reminiscent of the atomic number of elements.

An infinite Universe of Cluster Series

Transition metal carbonyl clusters like boranes portray an infinite number of series¹¹.The series were deduced from the cluster table series generated using the cluster number (k-value)¹². For small clusters, the k value corresponds to the number of bonds linking up the skeletal atoms that obey the 8-electron rule or the 18-electron rule. The cluster number is calculated using a simple empirical formula given by k = ½ (E-V) where E is the sum of octet electrons in case of main group elements or eighteen electrons in case of transition metals. This is summarized in Tables 1 and 2.

On closer analysis of cluster tables further revealed that the clusters portray an infinite number of clusters series based on 14n and 4n as bases for transition metals and main group elements respectively and these are shown in a selected short Table 3. Looking at table 3, it is quite clear that the series increase by steps of 2 as you go down the table or decrease in steps of 2 as you go up the table. Further scrutiny of the cluster tables^11-12 indicated that the cluster number k is related to the corresponding clusters series by 2n plus or minus one-half a multiple of 2. For instance if the series S = 14n + 8 the corresponding k value will be 2n-4 while for the S = 14n-30, the k value will be 2n+15. The k values for the transition metal cluster will be the same as the corresponding main group element cluster. Selected examples showing the calculation of a cluster number using the cluster series are given in Tables 4 and 5 for main group element and transition metal carbonyl clusters.

Table1: The sample showing selected main group elements for illustrating the basis for the empirical formula k = ½ (E-V)

Cluster	Observed number of skeletal bonds	number of skeletal elements (n)	E = 8n	Total Valence electrons (V)	k = ½ (E-V)
N₂	3	2	16	10	3
O₂	2	2	16	12	2
F₂	1	2	16	14	1
C₂H₂	3	2	16	10	3
C₂H₄	2	2	16	12	2
Cyclic C₃H₆	3	3	24	18	3
Cyclic C₄H₄	6	4	32	20	6
Cyclic C₆H₆	9	6	48	30	9
P₄	6	4	32	20	6
Bi₅³⁺	9	5	40	22	9

Table 2: The sample showing selected Transition metal elements for illustrating the basis for the empirical formula k = ½ (E-V)

Cluster Complex

Observed number of bonds

number of skeletal elements (n)

E = 18n

Total Valence electrons (V)k = ½ (E-V)Mn₂(CO)₁₀1236341Tc₂(CO)₁₀1236341Re₂(CO)₁₀1236341Co₂(CO)₈1236341Rh₂(CO)₈1236341Ir₂(CO)₈1236341Fe₂(CO)₉1236341Fe₃(CO)₁₂3354483Ru₃(CO)₁₂3354483Os₃(CO)₁₂3354483Co₄(CO)₁₂6472606Rh₄(CO)₁₂6472606Ir₄(CO)₁₂6472606Fe₄(C)(CO)₁₂²^―5472625Os₄(CO)₁₆4472644Os₅(CO)₁₆9590729Fe₅(C)(CO)₁₅8590748Rh₆(C)(CO)₁₅²^―96108909Os₆(CO)₁₈1261088412

Table 3: Portion of Cluster Series for Main Group Elements and Transition Metal Carbonyl Clusters

TRANSTION METAL CARBONYL CLUSTER SERIES(14n)	MAIN GROUP CLUSTER SERIES(4n)	k SERIES	REMARKS
14n-20	4n-20	2n+10
14n-18	4n-18	2n+9
14n-16	4n-16	2n+8
14n-14	4n-14	2n+7
14n-12	4n-12	2n+6
14n-10	4n-10	2n+5	Hexacapped Series(C⁶C)
14n-8	4n-8	2n+4	Pentacapped Series (C⁵C)
14n-6	4n-6	2n+3	Tetracapped Series(C⁴C)
14n-4	4n-4	2n+2	Tricapped Series(C³C)
14n-2	4n-2	2n+1	Bicapped Series (C²C)
14n	4n	2n	Monocapped Series(C¹C)
14n +2	4n+2	2n-1	Closo Series(C)
14n +4	4n+4	2n-2	Nido Series(N)
14n +6	4n+6	2n-3	Arachno Series(A)
14n +8	4n+8	2n-4	Hypho Series(H)
14n +10	4n+10	2n-5	Klapo Series( H-1)
14n +12	4n+12	2n-6
14n +14	4n+14	2n-7
14n +16	4n+16	2n-8
14n +18	4n+18	2n-9
14n +20	4n+20	2n-10

Table 4: Selected simple clusters showing Relationship between the Cluster k value and the corresponding Series for Main Group Elements

Cluster	Number of Skeletal elements(n)	4n	Valence electrons(V)	Series(S)	k-series	k value
N₂	2	8	10	4n+2	2n-1	3
O₂	2	8	12	4n+4	2n-2	2
F₂	2	8	14	4n+6	2n-3	1
C₂H₂	2	8	10	4n+2	2n-1	3
C₂H₄	2	8	12	4n+4	2n-2	2
P₄	4	16	20	4n+4	2n-2	6
Bi₅³⁺	5	20	22	4n+2	2n-1	9

Table 5: Relationship between the Cluster k value and the corresponding Series for carbonyl clusters

Cluster	Number of Skeletal elements(n)	14n	Valence electrons(V)	Series(S)	Cluster Type	k-series	k value
Mn₂(CO)₁₀	2	28	34	14n+6	Arachno	2n-3	1
Fe₃(CO)₁₂	3	42	48	14n+6	Arachno	2n-3	3
Co₄(CO)₁₂	4	56	60	14n+4	Nido	2n-2	6
Fe₄(C)(CO)₁₂²^―	4	56	62	14n+6	Arachno	2n-3	5
Os₄(CO)₁₆	4	56	64	14n+8	Hypho	2n-4	4
Os₅(CO)₁₆	5	70	72	14n+2	Closo	2n-1	9
Fe₅(C)(CO)₁₅	5	70	74	14n+4	Nido	2n-2	8
Os₆(CO)₁₈	6	84	84	14n	Monocapped	2n	12

Classification of Transition metal Carbonyls Using the 14n Rule

The 14n rule is extremely useful in categorization of a cluster into its series given the formula of the cluster. This method is exceedingly simple and rapid. The idea is to compare the reference value (14n) with the total valence electrons(V) of the cluster. If 14n is less than V, then the shortfall must be added to the 14n value to be equal to V value. On the other hand if 14n value is greater than V value, the excess must be subtracted to balance the V value. In so doing a cluster series of the complex is derived. It may be represented as S = 14n ± q, where S represents the cluster series, n the number of skeletal cluster atoms, and q is a multiple of 2. This concept is illustrated in scheme 1.

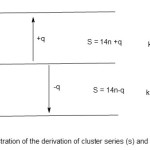Scheme 1

Click here to View scheme

A cluster number is given by k = 2n± q/2. The k value formula applies to both main group elements which obey the octet rule and transition metal skeletal elements which obey the 18-electron rule.The following selected examples are utilized for illustrations.

For example, Os₃(CO)₁₂: n = 3, 14n = 14×3 = 42. The number of valence electrons(V) = 8×3+2×12 = 48. The baseline reference 14n is less than V by 6. Hence the cluster series for the complex is S = 14n+6 and the cluster k value is k = 2n-3 = 6-3=3. The osmium atom form a triangular shape(k =3). Furthermore, the cluster belongs toArachnoseries(see Table 3). Consider OS₄(CO)₁₄; n = 4, 14n = 56, V = 60. Hence, S = 14n+4. This means that the cluster belong to the Nido series(see Table 3) and its cluster number k = 2n-2 = 6. The osmium skeletal atoms form a tetrahedral shape. Os₅(CO)₁₆; n = 5, 14n = 70 and V = 72. The cluster belongs to the series S= 14n+2. This is a member of Clososeries(see Table 3). The cluster number k = 2n-1 = 9. This corresponds to a trigonalbipyramidal geometry. For Os₅(CO)₁₉; n =5, 14n = 70 and V = 78. This gives us the series S = 14n +8 (Hypho series). The cluster number k = 2n-4 = 6. The shape of the osmium skeletal atoms is two edge-linked triangles. Consider Co₆(CO)₁₅(C)²^― cluster, n = 6, 14n = 84 and V = 90. Hence, S = 14n+6. This cluster belongs to an Arachno series with cluster number k = 2n-3 = 9. This is expected to have a trigonal prism shape as is observed⁷. Take another example Ru₆C(CO)₁₇; n = 6, 14n = 84 and V = 86. Therefore the cluster belongs to the cluster series S = 14n+2. This a member of Closo series with k = 2n-1 = 11. This is expected to have an octahedral shape as is reported.

The Capping Process and Capping Series:-The Presence of a Nuclear Cluster Inner Core

Using the series approach, the capped clusters can also easily be identified. For instance in the case of Os₆(CO)₁₈, n = 6, 14n = 84, V = 84. Hence S= 14n = C¹C which belongs to mono-capped series. The cluster number k = 2n = 12. Since it has six skeletal elements, it means the capping will be on the remaining five atoms. In this coding, this is expressed as C¹C[M-5]. The symbol M-5 corresponds to B₅H₅²^―closoborane ion which has a trigonalbipyramid geometry. The analysis of the series, reveals that the capping process involves a change in one skeletal atom and cluster number by 3 (∆k = 3) and valence electrons by 12. This is expressed as (1, 3, 12). In case of osmium, this is equivalent to changing a cluster by Os(CO)₂ fragment since Os donates 8 valence electrons and the two CO ligands donate 4. According to the coding system we designed in our study of clusters*, the complex Os₆(CO)₁₈ can be expressed as M-6-12-84 where 6 denotes the number of cluster elements M, 12 denotes the cluster number k and 84 the number of cluster valence electrons. The capping in Os₆(CO)₁₈ cluster can be traced in a decreasing or increasing manner. This is summarized in scheme 2. The gradual increase in capping fromOs₆(CO)₁₈ cluster is shown in scheme 3. Some of the clusters shown in the scheme may not be known as this is a hypothetical model. Hence the capping from Os₆(CO)₁₈ upwards may be represented as C¹C[M-5]→C²C[M-5]→C³C[M-5]→C⁴C[M-5]→C⁵C[M-5] and so on. Since, in principle, the capping of [M-5] inner core can go from 1 to 2, 3, 4, 5, 6 and so on, the inner cluster in this case [M-5] may be regarded as the Nuclear Cluster Inner Core of the complex. Many inner core cluster units have been revealed using the series number theory. Selected cluster complexes with inner core clusters are given in Table 6.

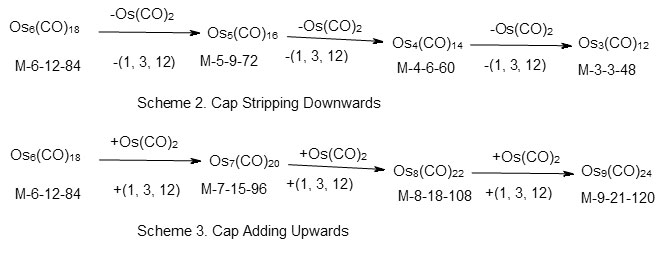
Scheme 2

Capping the Octahedral [M-6]Clusters

Let us consider the capping of an octahedral complex. One of the well known octahedral cluster is B₆H₆²^―. For this cluster of the main group element, n =6, 4n =24 and V = 26. Hence S = 4n+2. This means the cluster is a member of the Closo series. The six boron atoms arrange themselves in an octahedral shape (O_h). The cluster number is given by k = 2n-1 = 11 and the cluster code is M-6-11-26. The corresponding osmium cluster complex is Os₆(CO)₁₈^2―. In this case also, n =6, 14n = 84 and V = 86. Thus, S = 14n +2 which places the complex into the category of Closo series. The osmium skeletal atoms occupy an octahedral geometry (O_h) and the cluster number is given by 2n-1 = 11. Hence the cluster code is M-6-11-86. Comparing the cluster series (14n+2) of transition metal cluster with that of the corresponding main group series (4n +2), the difference in the number of valence electrons is 10n. Thus, (14n+2-10n = 4n +2). In the case of the six transition metal skeletal elements we can subtract (6×10 =60) from 86 valence electrons and we arrive at 26 electrons. This removal of 10 electrons from each of the 6 skeletal osmium elements is as if each osmium atom has lost a d¹⁰ electrons in so doing the cluster is transformed into that of the main group elements. Hence, M-6-11-86 removal of 60 electrons becomes M-6-11-26 and resembles the boranecloso cluster B₆H₆^2―. Alternatively, we can add 10n to the 26 electrons and get 86. This is summed up in scheme 4.

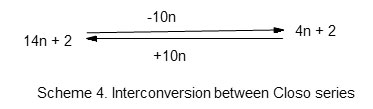
Scheme 4

Interconversion among other corresponding series of the main group elements and transition metal carbonyl clusters can be done in the same way. This relationship is what is also expressed in Table 3. As discussed earlier, the capping step-wise constant can numerically be represented as (1, 3,12). Hence, the octahedral capping on Os₆(CO)₁₈²^―[M-6-11-86] can be expressed as M-6-11-86 +(1,3,12)→M-7-14-98. This will give us the mono-capped cluster as observed in Os₇(CO)₂₁. In theOs₇(CO)₂₁ cluster, n = 7, 14n =98 and V= 98. Hence the cluster series S = 14n . The cluster capping will be given by C_p = C¹C. Since one of the seven skeletal atoms will get involved in capping, the rest will constitute the inner core and the symbol C¹C[M-6] can be used to represent a mono-capped cluster and k = 2n =14 and the cluster code becomes M-7-14-98. Continuing the process of capping, M-7-14-98 +(1,3,12)→M-8-17-110. This is a bi-capped cluster. A representative example is Os₈(CO)₂₂²^―; n =8, 14n = 112, V = 110. Hence S =14n-2 and C_p =C¹+C¹ = C²C. Since 14n represents the first capped series, for every (-2) added represents an additional capped series. Hence S= 14n-2 series symbolically corresponds toC_p= C¹+C¹ = C²C. This is a bi-capped series. Since 2 atoms of the 8 osmium atoms are used to form caps, the remaining six may be regarded to constitute the INNER CLUSTER CORE [M-6]. The symbol for the bi-capped octahedral cluster in this article may

be represented asC_p =C²C[M-6]. For ease of identifying cluster series including those which involve capping, it is deemed fit to use the capping symbol as C^xC[M-n] where x = 1,2, 3,4, 5,6,.. , M – represents the cluster element and n the number of the cluster elements in the nucleus. In fact, on deeper analysis of the series, the symbol [M-n] corresponds to a closoborane cluster. For instance, [M-4] Ξ B₄H₄²^―, [M-5] Ξ B₅H₅²^―, [M-6] Ξ B₆H₆²^― and so on.

Let us illustrate this approach to cluster categorization on some more examples for illustration. For example Os₉H(CO)₂₄^― cluster, n =9, 14n = 126, V = 122. The cluster series S =14n-4. This the same as{14n-2(2)}. According to cluster series symbol, this equivalent toC_p= C¹+C² = C³C[M-6]. Therefore, it is a tri-capped complex based on an octahedral nuclear core.In the case of Rh₁₀(CO)₂₁²^― cluster, n = 10, 14n = 140, V = 134. Therefore S = 14n-6→{14n-3(2)}. This gives us C_p = C¹+C³ = C⁴C[M-6]. This means this is a tetra-capped cluster with an octahedral nuclear cluster inner core. This applies the same forOs₁₀(CO)₂₆²^―comple;, n = 10, 14n = 140 and V= 134. Hence S = 14n-6. Symbolically in terms of cluster series, this corresponds to {14n-3(2)} andC_p = C¹ + C³ = C⁴C[M-6]. This is a tetra-capped cluster on an octahedral cluster nucleus. We can take another illustration on another example, Pd₆Ru₆(CO)₂₄²^―; n =12, 14n = 168 and V= 158. Hence S = 14n -10. In cluster series, symbolically, this corresponds to {14n-5(2)} and C_p = C¹ + C⁵ = C⁶C[M-6]. Thus, the cluster is a hexa-capped octahedral as reported in literature*. An amazing result is obtained when the method is applied to Ni₃₈Pt₆(CO)₄₈H⁵^― carbonyl cluster. In this case, n = 44, 14n = 616, V = 542. Hence S = 14n-74. This can be expressed as {14n-37(2)}. According to cluster series, this translates into C_p= C¹+ C³⁷ = C³⁸C[M-6]. This means that the cluster has an octahedral nuclear cluster core. The result is

indeed fascinating as an octahedral nuclear cluster comprising of six platinum atom are observed by x-ray structural analysis⁸.

Due to the simplicity of the method, a large number of clusters were categorized using the 14n rule. These results are given in Table 7, The table includes some of the clusters which have been categorized on the basis of their type of cluster nuclear core given in Table 6.In forming series,│∆k│ = 2 and │∆V│ = 14. In case of osmium carbonyl clusters, this corresponds to the fragment [Os(CO)₃ →8+6 = 14]. However in forming capping series, │∆k│ = 3 and │∆V│ = 12. This corresponds to the fragment [Os(CO)₂ →8+4 = 12]. On the basis of this information, a constructed series of osmium carbonyl clusters have been generated and are shown in Table 8. Johnsonetalhave generated similar clusters of ruthenium carbonyls in their EDESI-MS studies¹³.

Table6: Selected Capped Custer with Nuclear Inner cluster cores from M-2 to M-14

CLUSTER INNER CORE	CLUSTER	CLUSTER SERIES (S)	CLUSTER k VALUE	CAPPING SERIES (C_p)

M-2	Ru₈Pt(CO)₁₉²^―	14n-12	2n+6	C⁷C[M-2]
	Os₁₇(CO)₃₆²^―	14n-28	2n+14	C¹⁵C[M-2]
	Pd₃₅(CO)₂₃L₁₅	14n-64	2n+32	C³³C[M-2]

M-4	RuOs₅(CO)₁₄(C₆H₆)	14n-2	2n+1	C²C[M-4]
	Cu₂Ru₆(C)(CO)₁₆L₂	14n-6	2n+3	C⁴C[M-4]
	Pt₁₉(CO)₂₂⁴^―	14n-28	2n+14	C¹⁵C[M-4]
	Pd₂₃(CO)₂₀L₈	14n-36	2n+18	C¹⁹C[M-4]
	Pd₂₈Pt₁₃L₁₃H₁₂(CO)₂₇	14n-72	2n+36	C³⁷C[M-4]

M-5	Os₆(CO)₁₈	14n	2n	C¹C[M-5]
	Au₃Ru₄(CO)₁₂L₃H	14n-2	2n+1	C²C[M-5]
	Os₆Pt₂(CO)₁₆(COD)₂, COD =2e donor	14n-4	2n+2	C³C[M-5]
	Rh₉(CO)₁₉³^―	14n-6	2n+3	C⁴C[M-5]
	Os₇(CO)₁₉Au₂L₂ L₂ = Ph₂PCH₂CH₂PPh₂	14n-6	2n+3	C⁴C[M-5]
	Ru₈Pt₂(CO)₂₃H₂	14n-8	2n+4	C⁵C[M-5]
	Ru₇Pt₃(CO)₂₂H₂	14n-8	2n+4	C⁵C[M-5]
	Rh₁₄(CO)₂₅⁴^―	14n-16	2n+8	C⁹C[M-5]
	Rh₁₅(CO)₂₇³^―	14n-18	2n+9	C¹⁰C[M-5]

M-6	Os₇(CO)₂₁	14n	2n	C¹C[M-6]
	Re₇(C)(CO)₂₁³^―	14n	2n	C¹C[M-6]
	Rh₇(CO)₁₆³^―	14n	2n	C¹C[M-6]
	Os₇H₂(CO)₂₀	14n	2n	C¹C[M-6]
	Re₇(C)(CO)₂₁³^―	14n	2n	C¹C[M-6]
	Os₆Pt₂(CO)₁₇L₄	14n-2	2n+1	C²C[M-6]
	Os₈(CO)₂₂²^―	14n-2	2n+1	C²C[M-6]
	Ru₈H₂(CO)₂₁²^―	14n-2	2n+1	C²C[M-6]
	Os₈H(CO)₂₂^―	14n-2	2n+1	C²C[M-6]
	Os₈(C)(CO)₂₁	14n-2	2n+1	C²C[M-6]
	Re₈(C)(CO)₂₄²^―	14n-2	2n+1	C²C[M-6]
	Os₉(CO)₂₄²^―	14n-4	2n+2	C³C[M-6]
	Os₉H(CO)₂₄^―	14n-4	2n+2	C³C[M-6]
	Rh₉(CO)₁₉³^―	14n-4	2n+2	C³C[M-6]
	Pt₃Ru₆(C)(CO)₁₆L₄	14n-4	2n+2	C³C[M-6]
	PtRh₈(CO)₁₉²^―	14n-4	2n+2	C³C[M-6]
	Ru₁₀(C)(CO)₂₄²^―	14n-6	2n+3	C⁴C[M-6]
	Os₁₀(CO)₂₆²^―	14n-6	2n+3	C⁴C[M-6]
	Os₁₀(C)(CO)₂₄²^―	14n-6	2n+3	C⁴C[M-6]
	Os₁₀(H)₄(CO)₂₄²^―	14n-6	2n+3	C⁴C[M-6]
	Rh₁₀(CO)₂₁²^―	14n-6	2n+3	C⁴C[M-6]
	Pd₆Ru₆(CO)₂₄²^―	14n-10	2n+5	C⁶C[M-6]
	Ir₁₂(CO)₂₄²^―	14n-10	2n+5	C⁶C[M-6]
	Rh₁₃H₃(CO)₂₄²^―	14n-12	2n+6	C⁷C[M-6]
	Rh₁₃H₂(CO)₂₄³^―	14n-12	2n+6	C⁷C[M-6]
	Rh₁₃H(CO)₂₄⁴^―	14n-12	2n+6	C⁷C[M-6]
	Ir₁₄(CO)₂₇²^―	14n-14	2n+7	C⁸C[M-6]
	Os₁₀(C)(CO)₂₄Au(AuL)₃, L=PPh₃	14n-14	2n+7	C⁸C[M-6]
	Pd₁₆Ni₄(CO)₂₂L₂²^―, L=PPh₃	14n-26	2n+13	C¹⁴C[M-6]
	Os₁₂Rh₉(Cl)(CO)₄₄	14n-28	2n+14	C¹⁵C[M-6]
	Pd₂₃(CO)₂₀L₁₀, L=PEt₃	14n-32	2n+16	C¹⁷C[M-6]
	Pt₂₄(CO)₃₀²^―	14n-34	2n+17	C¹⁸C[M-6]
	Pt₂₆(CO)₃₂²^―	14n-38	2n+19	C²⁰C[M-6]
	Pd₂₉(CO)₂₈L₇²^―	14n-44	2n+22	C²³C[M-6]
	Pt₃₈(CO)₄₄²^―	14n-62	2n+31	C³²C[M-6]
	Pd₃₃Ni₉(CO)₄₁L₆⁴^―	14n-70	2n+35	C³⁶C[M-6]
	Ni₃₈Pt₆(CO)₄₈H⁵^―	14n-74	2n+37	C³⁸C[M-6]

M-7	Ir₉(CO)₂₀³^―	14n-2	2n+1	C²C[M-7]
	Ru₆Pt₃(CO)₂₁H₄	14n-2	2n+1	C²C[M-7]
	Ir₉(CO)₁₉H⁴^―	14n-2	2n+1	C²C[M-7]
	Ir₃Ni₆(CO)₁₇³^―	14n-2	2n+1	C²C[M-7]
	Os₆Pt₄(CO)₂₂L₂	14n-4	2n+2	C³C[M-7]
	Os₁₁(C)(CO)₂₇²^―	14n-6	2n+3	C⁴C[M-7]
	Rh₁₁(CO)₂₃³^―	14n-6	2n+3	C⁴C[M-7]
	Ru₆Pt₃(AuL)₂(CO)₂₁H₂	14n-6	2n+3	C⁴C[M-7]
	Rh₁₂(CO)₂₅H₂	14n-8	2n+4	C⁵C[M-7]
	Os₁₁(C)(CO)₂₇(CuL)^―, L =NCMe	14n-8	2n+4	C⁵C[M-7]
	Fe₆Pd₆(CO)₂₄H³^―	14n-8	2n+4	C⁵C[M-7]
	Pt₃Ru₁₀(C)₂(CO)₂₆²^―	14n-10	2n+5	C⁶C[M-7]
	Ni₁₄Pt₁₀(CO)₃₀⁴^―	14n-32	2n+16	C¹⁷C[M-7]
	Ni₂₄Pt₁₄(CO)₄₄⁴^―	14n-60	2n+30	C³¹C[M-7]

M-8	Ru₁₀(C)(CO)₂₄²^―	14n-2	2n+1	C²C[M-8]
	Ir₁₂(CO)₂₆²^―	14n-6	2n+3	C⁴C[M-8]
	Pd₂₃(CO)₂₂L₁₀, L = PEt₃	14n-28	2n+14	C¹⁵C[M-8]


M-9	Ni₁₁(C)₂(CO)₁₅⁴^―	14n-2	2n+1	C²C[M-9]
	Co₃Ni₉(C)(CO)₂₀³^―	14n-4	2n+2	C³C[M-9]
	Ni₁₂(C)₂(CO)₁₆²^―	14n-4	2n+2	C³C[M-9]
	Co₂Ni₁₀(C)(CO)₂₀²^―	14n-4	2n+2	C³C[M-9]
	Co₁₃(C)₂(CO)₂₄³^―	14n-6	2n+3	C⁴C[M-9]
	Rh₁₄(N)₂(CO)₂₅²^―	14n-8	2n+4	C⁵C[M-9]
	Rh₁₅(C)₂(CO)₂₈^―	14n-10	2n+5	C⁶C[M-9]
	Pd₁₃Ni₁₃(CO)₃₄⁴^―	14n-32	2n+16	C¹⁷C[M-9]

M-10	Rh₁₂(C)₂(CO)₂₃⁴^―	14n-2	2n+1	C²C[M-10]
	Rh₁₂(C)₂(CO)₂₄²^―	14n-2	2n+1	C²C[M-10]
	Rh₁₂(C)₂(CO)₂₅	14n-2	2n+1	C²C[M-10]
	Ag₁₃Fe₈(CO)₃₂³^―	14n-20	2n+10	C¹¹C[M-10]

M-11	Fe₆Ni₆(N)₂(CO)₂₄²^―	14n	2n	C¹C[M-11]
	Os₁₈Hg₂(C)₂(CO)₄₂⁴^―	14n-16	2n+8	C⁹C[M-11]
	Rh₂₈(N)₄(CO)₄₁H₄⁴^―	14n-32	2n+16	C¹⁷C[M-11]
	Au₆Ni₃₂(CO)₄₄⁶^―	14n-52	2n+26	C²⁷C[M-11]

M-13	Co₁₄(N)₃(CO)₂₆³^―	14n	2n	C¹C[M-13]
	Rh₁₅(C)₂(CO)₃₀³^―	14n-2	2n+1	C²C[M-13]
	Rh₁₇(S)₂(CO)₃₂³^―	14n-6	2n+3	C⁴C[M-13]

M-14	Rh₂₃(CO)₃₈(N)₄³^―	14n-16	2n+8	C⁹C[M-14]

Table 7: Selected examples of carbonyl clusters categorized using the 14n rule

14n +8 (HYPHO); k = 2n-4	14n +6 (ARACHNO); k =2n-3	14n +4 (NIDO); k =2n-2
Mn₃(CO)₁₄^―(50, 2)

Os₅(CO)₁₉(78, 6)

Co₆(P)(CO)₁₆^―(92, 8)

Ni₈L₆(CO)₈(120, 12), L = PPh₃Mn₂(CO)₁₀(34, 1)

Ni₂(C_p)₂(CO)₂(34, 1)

Os₃(CO)₁₂(48, 3)

Fe₄(C)(CO)₁₃(62, 5)

Rh₆(C)(CO)₁₅²^―(90, 9)

Ni₈(C)(CO)₁₆²^―(118, 13)Rh₂(C_p)₂(CO)₂(32, 2)

Co₄(CO)₁₂(60,6)

Fe₅(C)(CO)₁₅(74, 8)

Os₆Pt(CO)₁₈H₈(102, 12)

Ni₉(C)(CO)₁₇²^―(130, 16)14n+2 (CLOSO); k = 2n-114n(C¹C) MONOCAP; k = 2n14n-2(C²C) BICAP; k =2n+1Re₂(C_p)₂(CO)₃(30, 3)

Ru₄(CO)₁₂H₂(58, 7)

Os₅(CO)₁₆(72, 9)

Os₆(CO)₁₈²^―(86, 11); O_hmingos

Os₇H₂(CO)₁₉(110, 13)

Co₇(N)(CO)₁₅²^―(100, 13)

Rh₈(C)(CO)₁₉(114,15)

Rh₁₀(S)(CO)₂₂²^―(142, 19)

Rh₁₂(Sb)(CO)₂₇³^―(170, 23)Ru₄(CO)₁₂H₄(56, 8)

Os₆(CO)₁₈(84, 12)

Cu₃Fe₃(CO)₁₂³^―(84, 12)

Os₇(CO)₂₁(98, 14)

Rh₇(CO)₁₆³^―(98, 14)

Pt₂Ru₅(C)(CO)₁₅²^―(98,14)

Co₁₁N₂(CO)₂₁³^―(154, 22)

Fe₆Ni₆N₂(CO)₂₄²^―(168, 24)

Rh₁₂C₂(CO)₂₄²^―(168, 24)

Pt₃Ru₁₀C₂(CO)₃₁²^―(182, 26)

Pt₃Os₄(CO)₁₁L₆(96,15), L =2e donor

Os₈(CO)₂₂²^―(110, 17)

Re₈(C)(CO)₂₄²^―(110,17)

Os₆Pt₂(CO)₁₇L₄(110,17)

Ru₈H₂(CO)₂₁²^―(110, 17)

Ir₉(CO)₂₀³^―(124, 19)

Ru₆Pt₃(CO)₂₁H₃^―(124, 19)

Ru₁₀C₂(CO)₂₄²^―(138,21)

Co₃Ni₇C₂(CO)₁₅³^―(138, 21)

Rh₁₂(CO)₂₅C₂(166, 25)

14n-4 (C³C) TRICAP; k = 2n +214n-6 (C⁴C) TETRACAP; k =2n+314n-8 (C⁵C) PENTACAP; k =2n+4

14n-10 (C⁶C) HEXACAP; k = 2n+5	14n-12 (C⁷C); k =2n+6	14n-14 (C⁸C) ; k =2n+7
Ir₁₂(CO)₂₄²^―(158, 29)

Pt₃Ru₁₀C₂(CO)₂₆²^―(172, 31)

Rh₁₅C₂(CO)₂₈^―(200,35)

Rh₁₃(CO)₂₄H₂³^―(170, 32)

Rh₁₃(CO)₂₄H⁴^―(170, 32)Ir₁₄(CO)₂₇²^―(182, 35)

14n-16(C⁹C); k = 2n+814n-18(C¹⁰C); k =2n+914n-20(C¹¹C); k =2n+10Rh₁₄(CO)₂₅⁴^―(180, 36)

Ir₁₄(CO)₂₇(180, 36)

Rh₁₄(CO)₂₆²^―(180, 36)

Os₁₀(CO)₂₄(AuL)₄(180, 36), L = PPh₂Me

Os₁₈Hg₂(CO)₄₂C₂⁴^―(264, 48)

[Os₁₀(CO)₂₄(C)]₂Hg²^―(278, 50)

Rh₁₅(CO)₂₇³^―(192, 39)

Rh₂₃(CO)₃₈N₄^―(304, 55)Pd₁₆(CO)₁₃L₉(204, 42)

Ag₁₃Fe₈(CO)₃₂³^―(274, 52)

Hg₃[Ru₉(C)(CO)₂₁]₂²^―(274, 52)

14n-22(C¹²C); k =2n+1114n-24(C¹³C); k =2n+1214n-26(C¹⁴C); k =2n+13Rh₁₇(CO)₃₀³^―(216, 45)

Os₁₈Hg₂(CO)₄₀C₂²^―(258, 51) Pd₁₆Ni₄(CO)₂₂L₄²^―(254, 53)

L = PPh₃

Os₁₈Pd₃C₂(CO)₄₂²^―(268, 55)

Ni₃₂C₆(CO)₃₆⁶^―(422, 77)14n-28(C¹⁵C); k = 2n+1414n-30(C¹⁶C) ; k = 2n+1514n-32(C¹⁷C) ; k = 2n+16Os₁₇(CO)₃₆²^―(210, 48)

Pt₁₉(CO)₂₂⁴^―(238, 52)

Pd₂₃(CO)₂₂L₁₀(294, 60), L =PEt₃

Rh₂₂(CO)₃₇⁴^―(276, 60)

Pt₄Rh₁₈(CO)₃₅⁴^―(276, 60)

Ni₁₄Pt₁₀(CO)₃₀⁴^―(304, 64)

Pd₁₃Ni₁₃(CO)₃₄⁴^―(332, 68)

Rh₂₈(CO)₄₁H₂N₄⁴^―(360, 72)14n-38(C²⁰C) ; k = 2n+1914n-44(C²³C) ; k = 2n+2214n-64(C³³C) ; k = 2n+32Os₂₀(CO)₄₀²^―(242, 59)

Pt₂₆(CO)₃₂²^―(326, 71)

HNi₃₈(CO)₄₂C₆⁵^―(494, 95)

Pd₂₉(CO)₂₈L₇²^―(362, 80)

L = PPh₃

Pd₁₆Ni₁₆(CO)₄₀⁴^―(404, 86)

Pd₂₉Ni₃(CO)₄₀⁴^―(404, 86)Pd₃₄(CO)₂₄L₁₂(412, 100)

Pd₃₅(CO)₂₃L₁₅(426, 102)

Table 8: Constructed table of Osmium Carbonyl Clusters based on Simple Number Theory

HYPHO	ARACHNO	NIDO	CLOSO	MONOCAP	BICAP	TRICAP	TETRACAP

							Os₂(CO)₃
						Os₂(CO)₄	Os₃(CO)₆
					Os₂(CO)₅	Os₃(CO)₇	Os₄(CO)₉
				Os₂(CO)₆	Os₃(CO)₈	Os₄(CO)₁₀	Os₅(CO)₁₂
			Os₂(CO)₇	Os₃(CO)₉	Os₄(CO)₁₁	Os₅(CO)₁₃	Os₆(CO)₁₅
		Os₂(CO)₈	Os₃(CO)₁₀	Os₄(CO)₁₂	Os₅(CO)₁₄	Os₆(CO)₁₆	Os₇(CO)₁₈
	Os₂(CO)₉	Os₃(CO)₁₁	Os₄(CO)₁₃	Os₅(CO)₁₅	Os₆(CO)₁₇	Os₇(CO)₁₉	Os₈(CO)₂₁
Os₂(CO)₁₀	Os₃(CO)₁₂	Os₄(CO)₁₄	Os₅(CO)₁₆	Os₆(CO)₁₈	Os₇(CO)₂₀	Os₈(CO)₂₂	Os₉(CO)₂₄
Os₃(CO)₁₃	Os₄(CO)₁₅	Os₅(CO)₁₇	Os₆(CO)₁₉	Os₇(CO)₂₁	Os₈(CO)₂₃	Os₉(CO)₂₅	Os₁₀(CO)₂₇
Os₄(CO)₁₆	Os₅(CO)₁₈	Os₆(CO)₂₀	Os₇(CO)₂₂	Os₈(CO)₂₄	Os₉(CO)₂₆	Os₁₀(CO)₂₈	Os₁₁(CO)₃₀

HYPHO	ARACHNO	NIDO	CLOSO	MONOCAP	BICAP	TRICAP	TETRACAP
Os₂(CO)₁₀	Os₃(CO)₁₂	Os₄(CO)₁₄	Os₅(CO)₁₆	Os₆(CO)₁₈	Os₇(CO)₂₀	Os₈(CO)₂₂	Os₉(CO)₂₄
Os₃(CO)₁₃	Os₄(CO)₁₅	Os₅(CO)₁₇	Os₆(CO)₁₉	Os₇(CO)₂₁	Os₈(CO)₂₃	Os₉(CO)₂₅	Os₁₀(CO)₂₇
Os₄(CO)₁₆	Os₅(CO)₁₈	Os₆(CO)₂₀	Os₇(CO)₂₂	Os₈(CO)₂₄	Os₉(CO)₂₆	Os₁₀(CO)₂₈	Os₁₁(CO)₃₀
Os₅(CO)₁₉	Os₆(CO)₂₁	Os₇(CO)₂₃	Os₈(CO)₂₅	Os₉(CO)₂₇	Os₁₀(CO)₂₉	Os₁₁(CO)₃₁	Os₁₂(CO)₃₃
Os₆(CO)₂₂	Os₇(CO)₂₄	Os₈(CO)₂₆	Os₉(CO)₂₈	Os₁₀(CO)₃₀	Os₁₁(CO)₃₂	Os₁₂(CO)₃₄	Os₁₃(CO)₃₆
Os₇(CO)₂₅	Os₈(CO)₂₇	Os₉(CO)₂₉	Os₁₀(CO)₃₁	Os₁₁(CO)₃₃	Os₁₂(CO)₃₅	Os₁₃(CO)₃₇	Os₁₄(CO)₃₉
Os₈(CO)₂₈	Os₉(CO)₃₀	Os₁₀(CO)₃₂	Os₁₁(CO)₃₄	Os₁₂(CO)₃₆	Os₁₃(CO)₃₈	Os₁₄(CO)₄₀	Os₁₅(CO)₄₂
Os₉(CO)₃₁	Os₁₀(CO)₃₃	Os₁₁(CO)₃₅	Os₁₂(CO)₃₇	Os₁₃(CO)₃₉	Os₁₄(CO)₄₁	Os₁₅(CO)₄₃	Os₁₆(CO)₄₅
Os₁₀(CO)₃₄	Os₁₁(CO)₃₆	Os₁₂(CO)₃₈	Os₁₃(CO)₄₀	Os₁₄(CO)₄₂	Os₁₅(CO)₄₄	Os₁₆(CO)₄₆	Os₁₇(CO)₄₈
Os₁₁(CO)₃₇	Os₁₂(CO)₃₉	Os₁₃(CO)₄₁	Os₁₄(CO)₄₃	Os₁₅(CO)₄₅	Os₁₆(CO)₄₇	Os₁₇(CO)₄₉	Os₁₈(CO)₅₁
Os₁₂(CO)₄₀	Os₁₃(CO)₄₂	Os₁₄(CO)₄₄	Os₁₅(CO)₄₆	Os₁₆(CO)₄₈	Os₁₇(CO)₅₀	Os₁₈(CO)₅₂	Os₁₉(CO)₅₄
Os₁₃(CO)₄₃	Os₁₄(CO)₄₅	Os₁₅(CO)₄₇	Os₁₆(CO)₄₉	Os₁₇(CO)₅₁	Os₁₈(CO)₅₃	Os₁₉(CO)₅₅	Os₂₀(CO)₅₇
Os₁₄(CO)₄₆	Os₁₅(CO)₄₈	Os₁₆(CO)₅₀	Os₁₇(CO)₅₂	Os₁₈(CO)₅₄	Os₁₉(CO)₅₆	Os₂₀(CO)₅₈	Os₂₁(CO)₆₀
Os₁₅(CO)₄₉	Os₁₆(CO)₅₁	Os₁₇(CO)₅₃	Os₁₈(CO)₅₄	Os₁₉(CO)₅₇	Os₂₀(CO)₅₉	Os₂₁(CO)₆₁	Os₂₂(CO)₆₃
Os₁₆(CO)₅₂	Os₁₇(CO)₅₄	Os₁₈(CO)₅₆	Os₁₉(CO)₅₇	Os₂₀(CO)₆₀	Os₂₁(CO)₆₂	Os₂₂(CO)₆₄	Os₂₃(CO)₆₆
Os₁₇(CO)₅₅	Os₁₈(CO)₅₇	Os₁₉(CO)₅₉	Os₂₀(CO)₆₀	Os₂₁(CO)₆₃	Os₂₂(CO)₆₅	Os₂₃(CO)₆₇	Os₂₄(CO)₆₉
Os₁₈(CO)₅₈	Os₁₉(CO)₆₀	Os₂₀(CO)₆₂	Os₂₁(CO)₆₃	Os₂₂(CO)₆₆	Os₂₃(CO)₆₈	Os₂₄(CO)₇₀	Os₂₅(CO)₇₂
Os₁₉(CO)₆₁	Os₂₀(CO)₆₃	Os₂₁(CO)₆₅	Os₂₂(CO)₆₆	Os₂₃(CO)₆₉	Os₂₄(CO)₇₁	Os₂₅(CO)₇₃	Os₂₆(CO)₇₅
Os₂₀(CO)₆₄	Os₂₁(CO)₆₆	Os₂₂(CO)₆₈	Os₂₃(CO)₆₉	Os₂₄(CO)₇₂	Os₂₅(CO)₇₄	Os₂₆(CO)₇₆	Os₂₇(CO)₇₈
Os₂₁(CO)₆₇	Os₂₂(CO)₆₉	Os₂₃(CO)₇₁	Os₂₄(CO)₇₂	Os₂₅(CO)₇₅	Os₂₆(CO)₇₇	Os₂₇(CO)₇₉	Os₂₈(CO)₈₁
Os₂₂(CO)₇₀	Os₂₃(CO)₇₂	Os₂₄(CO)₇₄	Os₂₅(CO)₇₅	Os₂₆(CO)₇₈	Os₂₇(CO)₈₀	Os₂₈(CO)₈₂	Os₂₉(CO)₈₄
Os₂₃(CO)₇₃	Os₂₄(CO)₇₅	Os₂₅(CO)₇₇	Os₂₆(CO)₇₈	Os₂₇(CO)₈₁	Os₂₈(CO)₈₃	Os₂₉(CO)₈₅	Os₃₀(CO)₈₇
Os₂₄(CO)₇₆	Os₂₅(CO)₇₈	Os₂₆(CO)₈₀	Os₂₇(CO)₈₁	Os₂₈(CO)₈₄	Os₂₉(CO)₈₆	Os₃₀(CO)₈₈	Os₃₁(CO)₉₀
Os₂₅(CO)₇₉	Os₂₆(CO)₈₁	Os₂₇(CO)₈₃	Os₂₈(CO)₈₄	Os₂₉(CO)₈₇	Os₃₀(CO)₈₉	Os₃₁(CO)₉₁	Os₃₂(CO)₉₃
Os₂₆(CO)₈₂	Os₂₇(CO)₈₄	Os₂₈(CO)₈₆	Os₂₉(CO)₈₇	Os₃₀(CO)₉₀	Os₃₁(CO)₉₁	Os₃₂(CO)₉₄	Os₃₃(CO)₉₆
Os₂₇(CO)₈₅	Os₂₈(CO)₈₇	Os₂₉(CO)₈₉	Os₃₀(CO)₉₀	Os₃₁(CO)₉₃	Os₃₂(CO)₉₄	Os₃₃(CO)₉₇	Os₃₄(CO)₉₉
Os₂₈(CO)₈₈	Os₂₉(CO)₉₀	Os₃₀(CO)₉₂	Os₃₁(CO)₉₃	Os₃₂(CO)₉₆	Os₃₃(CO)₉₇	Os₃₄(CO)₁₀₀	Os₃₅(CO)₁₀₂
Os₂₉(CO)₉₁	Os₃₀(CO)₉₃	Os₃₁(CO)₉₅	Os₃₂(CO)₉₆	Os₃₃(CO)₉₉	Os₃₄(CO)₁₀₀	Os₃₅(CO)₁₀₃	Os₃₆(CO)₁₀₅
Os₃₀(CO)₉₄	Os₃₁(CO)₉₆	Os₃₂(CO)₉₈	Os₃₃(CO)₉₉	Os₃₄(CO)₁₀₂	Os₃₅(CO)₁₀₃	Os₃₆(CO)₁₀₆	Os₃₇(CO)₁₀₈

TETRACAP	PENTACAP	HEXACAP	HEPTACAP	OCTACAP	NONACAP	DECACAP
Os₉(CO)₂₄	Os₁₀(CO)₂₆	Os₁₁(CO)₂₈	Os₁₂(CO)₃₀	Os₁₃(CO)₃₂	Os₁₄(CO)₃₄	Os₁₅(CO)₃₅
Os₁₀(CO)₂₇	Os₁₁(CO)₂₉	Os₁₂(CO)₃₁	Os₁₃(CO)₃₃	Os₁₄(CO)₃₅	Os₁₅(CO)₃₇	Os₁₆(CO)₃₉
Os₁₁(CO)₃₀	Os₁₂(CO)₃₂	Os₁₃(CO)₃₄	Os₁₄(CO)₃₆	Os₁₅(CO)₃₈	Os₁₆(CO)₄₀	Os₁₇(CO)₄₂
Os₁₂(CO)₃₃	Os₁₃(CO)₃₅	Os₁₄(CO)₃₇	Os₁₅(CO)₃₉	Os₁₆(CO)₄₁	Os₁₇(CO)₄₃	Os₁₈(CO)₄₅
Os₁₃(CO)₃₆	Os₁₄(CO)₃₈	Os₁₅(CO)₄₀	Os₁₆(CO)₄₂	Os₁₇(CO)₄₄	Os₁₈(CO)₄₆	Os₁₉(CO)₄₈
Os₁₄(CO)₃₉	Os₁₅(CO)₄₁	Os₁₆(CO)₄₃	Os₁₇(CO)₄₅	Os₁₈(CO)₄₇	Os₁₉(CO)₄₉	Os₂₀(CO)₅₁
Os₁₅(CO)₄₂	Os₁₆(CO)₄₄	Os₁₇(CO)₄₆	Os₁₈(CO)₄₈	Os₁₉(CO)₅₀	Os₂₀(CO)₅₂	Os₂₁(CO)₅₄
Os₁₆(CO)₄₅	Os₁₇(CO)₄₇	Os₁₈(CO)₄₉	Os₁₈(CO)₅₁	Os₁₉(CO)₅₃	Os₂₀(CO)₅₅	Os₂₁(CO)₅₇
Os₁₇(CO)₄₈	Os₁₈(CO)₅₀	Os₁₉(CO)₅₂	Os₂₀(CO)₅₄	Os₂₁(CO)₅₆	Os₂₂(CO)₅₈	Os₂₃(CO)₆₀
Os₁₈(CO)₅₁	Os₁₉(CO)₅₃	Os₂₀(CO)₅₅	Os₂₁(CO)₅₇	Os₂₂(CO)₅₉	Os₂₃(CO)₆₁	Os₂₄(CO)₆₃
Os₁₉(CO)₅₄	Os₂₀(CO)₅₆	Os₂₁(CO)₅₈	Os₂₂(CO)₆₀	Os₂₃(CO)₆₂	Os₂₄(CO)₆₄	Os₂₅(CO)₆₆
Os₂₀(CO)₅₇	Os₂₁(CO)₅₉	Os₂₂(CO)₆₁	Os₂₃(CO)₆₃	Os₂₄(CO)₆₅	Os₂₅(CO)₆₇	Os₂₆(CO)₆₉
Os₂₁(CO)₆₀	Os₂₂(CO)₆₂	Os₂₃(CO)₆₄	Os₂₄(CO)₆₆	Os₂₅(CO)₆₈	Os₂₆(CO)₇₀	Os₂₇(CO)₇₂
Os₂₂(CO)₆₃	Os₂₃(CO)₆₅	Os₂₄(CO)₆₇	Os₂₅(CO)₆₉	Os₂₆(CO)₇₁	Os₂₇(CO)₇₃	Os₂₈(CO)₇₅
Os₂₃(CO)₆₆	Os₂₄(CO)₆₈	Os₂₅(CO)₇₀	Os₂₆(CO)₇₂	Os₂₇(CO)₇₄	Os₂₈(CO)₇₆	Os₂₉(CO)₇₈
Os₂₄(CO)₆₉	Os₂₅(CO)₇₁	Os₂₆(CO)₇₃	Os₂₇(CO)₇₅	Os₂₈(CO)₇₇	Os₂₉(CO)₇₉	Os₃₀(CO)₈₁
Os₂₅(CO)₇₂	Os₂₆(CO)₇₄	Os₂₇(CO)₇₆	Os₂₈(CO)₇₈	Os₂₉(CO)₈₀	Os₃₀(CO)₈₂	Os₃₁(CO)₈₄
Os₂₆(CO)₇₅	Os₂₇(CO)₇₇	Os₂₈(CO)₇₉	Os₂₉(CO)₈₁	Os₃₀(CO)₈₃	Os₃₁(CO)₈₅	Os₃₂(CO)₈₇
Os₂₇(CO)₇₈	Os₂₈(CO)₈₀	Os₂₉(CO)₈₂	Os₃₀(CO)₈₄	Os₃₁(CO)₈₆	Os₃₂(CO)₈₈	Os₃₃(CO)₉₀
Os₂₈(CO)₈₁	Os₂₉(CO)₈₃	Os₃₀(CO)₈₅	Os₃₁(CO)₈₇	Os₃₂(CO)₈₉	Os₃₃(CO)₉₁	Os₃₄(CO)₉₃
Os₂₉(CO)₈₄	Os₃₀(CO)₈₆	Os₃₁(CO)₈₈	Os₃₂(CO)₉₀	Os₃₃(CO)₉₂	Os₃₄(CO)₉₄	Os₃₅(CO)₉₆
Os₃₀(CO)₈₇	Os₃₁(CO)₈₉	Os₃₂(CO)₉₁	Os₃₃(CO)₉₃	Os₃₄(CO)₉₅	Os₃₅(CO)₉₇	Os₃₆(CO)₉₉
Os₃₁(CO)₉₀	Os₃₂(CO)₉₂	Os₃₃(CO)₉₄	Os₃₄(CO)₉₆	Os₃₅(CO)₉₈	Os₃₆(CO)₁₀₀	Os₃₇(CO)₁₀₂
Os₃₂(CO)₉₃	Os₃₃(CO)₉₅	Os₃₄(CO)₉₇	Os₃₅(CO)₉₉	Os₃₆(CO)₁₀₁	Os₃₇(CO)₁₀₃	Os₃₈(CO)₁₀₅
Os₃₃(CO)₉₆	Os₃₄(CO)₉₈	Os₃₅(CO)₁₀₀	Os₃₆(CO)₁₀₂	Os₃₇(CO)₁₀₄	Os₃₈(CO)₁₀₆	Os₃₉(CO)₁₀₈
Os₃₄(CO)₉₉	Os₃₅(CO)₁₀₁	Os₃₆(CO)₁₀₃	Os₃₇(CO)₁₀₅	Os₃₈(CO)₁₀₇	Os₃₉(CO)₁₀₉	Os₄₀(CO)₁₁₁
Os₃₅(CO)₁₀₂	Os₃₆(CO)₁₀₄	Os₃₇(CO)₁₀₆	Os₃₈(CO)₁₀₈	Os₃₉(CO)₁₁₀	Os₄₀(CO)₁₁₂	Os₄₁(CO)₁₁₄
Os₃₆(CO)₁₀₅	Os₃₇(CO)₁₀₇	Os₃₈(CO)₁₀₉	Os₃₉(CO)₁₁₁	Os₄₀(CO)₁₁₃	Os₄₁(CO)₁₁₅	Os₄₂(CO)₁₁₇
Os₃₇(CO)₁₀₈	Os₃₈(CO)₁₁₀	Os₃₉(CO)₁₁₂	Os₄₀(CO)₁₁₄	Os₄₁(CO)₁₁₆	Os₄₂(CO)₁₁₈	Os₄₃(CO)₁₂₀

Further Highlights on Transition Metal Carbonyl Clusters

Just as mononuclear transition metal carbonyl clusters such as Ni(CO)₄ and Fe(CO)₅ tend to obey the 18 electron rule, the transition metal carbonyl clusters such as Mn₂(CO)₁₀, Os₃(CO)₁₂ and Ir₄(CO)₁₂ tend to do the same. Hidden in the 18 electron rule is the attainment of the noble gas configuration. If we envisage a situation in which the CO ligands stealthily donate their electrons to the cluster skeleton atoms to enable them satisfy the 18 electron rule and go away, then in small clusters,the cluster number k would represent bonds or linkages. For instance k= 1 for Cl₂ giving a linear molecule and Mn₂(CO)₁₀ with k =1, the ‘Mn₂’ fragment will have a single bond or linkage. Also Rh₂(C_P*)₂(CO)₂, O₂, C₂H₄ with k = 2, the Rh₂ fragment, O₂ and C₂ fragment each is doubly bonded. The C₂H₂, and W₂(CO)₄(C_pMe)₂ with k =3, the fragments C₂ and W₂ are each triply bonded. Likewise, Os₃(CO)₁₂, cyclopropane,C₃H₆ with k =3 have the fragments Os₃ and C₃ forming triangular shapes. The P₄ molecule and Ir₄(CO)₁₂ have k= 6 and both the P₄ molecule and the Ir₄ fragment adopt a tetrahedral geometry. Furthermore, Os₅(CO)₁₆ and Bi₅³⁺have k= 9 and both the bismuth cluster ion and O₅ fragment adopt a trigonalbipyramid shape.

As the number of skeletal atoms in transition metal carbonyl clusters increases, the k value appear not to correspond to the skeletal linkages. For instance, in Os₆(CO)₁₈²^― and B₆H₆²^―, k =11 and both O₆ and B₆ fragments have an octahedral geometry. In such cases, it is better to regard the k value as simply a cluster number characteristic of the cluster as a member of the cluster series. The k value of 11 in this case is a number within the closo cluster series S = 14n+2 and k = 2n-1 with k values (∆k =2), 1,3, 5, 7, 9, 11, 13, 15, 17, .. and so forth. For the capping series, ∆k =3 and so for the octahedral closo value of k =11, will belong to the series k =2, 5, 8, 11,14, 17, 20, 23, .. and so on. In the coding system adopted in this article the capping is defined to as to commence after the closo series. In this particular case, k = 14 will represent a monocap (C¹C on an octahedral geometry,[M-6]), k = 17 a bicap(C²C[M-6]), k =20 a tricap(C¹C[M-6]) and so on.

Applying the 14n rule, carbonyl clusters from simple to medium to very complex ones can readily be categorized. In some cases, the k value can be utilized as a guide to predict the cluster geometry. Just as atoms and cells of plants and animals have nuclei, the closo unit in clusters around which the capping takes place may be considered to behave as a nuclear cluster inner core. In the complexes, Pd₆Ru₆(CO)₂₄²^―{C⁶C[M-6]} and Ni₃₈Pt₆(CO)₄₈H⁵^―{C³⁸C[M-6]} are both centered around an octahedral closo nucleus, while Os₆(CO)₁₈{C¹C[M-5]} and Ru₇Pt₃(CO)₂₂H₂{C⁵C[M-5]} are based on a closotrigonalbipyamid central core cluster unit. Using the 14n rule approach such cluster nuclei can readily be identified for a large number of clusters. The 4n rule is most appropriately utilized in categorization of clusters of the main group elements for systems which obey octet rule. The 14n and 4n rules of classifying clusters complements the existing methods currently being applied.

The Origin of the Empirical Formula k = ½ (E-V) and the Cluster Series

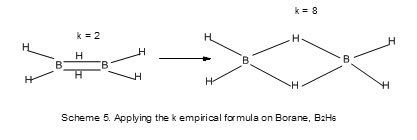
As can be seen, the application of the empirical formula, 14n and 4n rules to clusters is smooth, simple and straight forward. Therefore, it is extremely important to briefly explain their origin. In an attempt to find a simple equation to enable one easily draw a Lewis structure of simple known covalent molecules and ions, the empirical formula k = ½ (E-V) was born. Starting with N₂ molecule which has a triple bond and a lone pair on each electron and each atom obeying the octet rule, the sum of hypothetical octet electrons E= 2×8 = 16 and the sum of the valence electrons V = 2×5 = 10. Hence k = ½ (E-V) = 3, the same as the triple bond of the N₂molecule. Once the number of bonds 3 in this case for N₂ have been obtained the calculation representing six valence electrons, the remaining 4 constitute 2 lone pairs which are evenly distributed around the two nitrogen atoms giving rise to the needed Lewis structure of N₂.Using the same empirical formula, k =2 for O₂ and k =1 for F₂ and the Lewis structures can be obtained in the same manner. What is surprising, the empirical formula gave a k value of 4 for C₂ molecule in agreement with the recent reports* meaning that C₂ has a quadruple bond. This contradicts the molecular energy level diagram conventional result of C₂which gives a double bond.Table 1 gives more selected examples. When the empirical formula is applied to C₂H₂, E = 2X8 = 16 for the two carbon atoms which obey the octet rule and V = 2×4+2 = 10 , the sum of the valence electrons. The two hydrogen atoms are considered as donating additional electrons to assist the two carbon atoms satisfy the octet rule. The k value for the fragment ‘C₂’ in C₂H₂ is 3. This corresponds to the triple bond in the molecule. What is interesting is that if we assume that each of the hydrogen atoms in C₂H₂ also obeys the two(2) electron rule of [He] configuration, then the refined E for C₂H₂ will be 2×8+2×2= 20 and V= 10. The refined k value for C₂H₂ will be equal to ½ (20-10) = 5. This means all the bonds in C₂H₂ will be five including the triple bond. This is in agreement with the structure of C₂H₂. Using the same approach, the unrefined k value for C₂H₄is 2 and the refined one 6. This corresponds to the structure of C₂H₄. Diborane, B₂H₆ is isoelectronic to C₂H₄. When the empirical formula k = ½ (E-V) is applied to it, a value of 2 is obtained. Since the boron atom is electron deficient to satisfy the octet rule in the case of B₂H₆ unlike the C₂H₄ the additional two hydrogens may be considered to be donors of electrons to the double bond to enable the two boron atoms satisfy the octet rule. The calculation also gives a refined k value of 8. This is in agreement with the diborane banana bonds structure of diborane as is currently known. This simple calculation underpins the power of noble gas configuration and by implication the octet rule and now the helium rule for hydrogen atom.

schem6

A coding for the molecules showing the number of atoms, bonds and electrons in a given molecular formula was designed. The code is represented as (M-n-k-V) where M represents the atom that obeys the octet rule, k is the cluster number or bonds in the case of simple molecules and V is the total valence electrons. Analyzing this coding for molecules, the cluster series were developed. In the case of C₂ this becomes M-2-4-8. Arising from this code, it is clear that there is a relationship between the number of atoms(n) and valence electrons(V). This relationship is V= 4n =8 or in terms of series, S = 4n and k = 2n = 4. For the N₂ molecule, the code is M-2-3-10. In this case, V= 4n+2 = 10 and this gives us the series S = 4n+2 and k =2n-1. For the O₂ molecule, the code is M-2-2-12. This gives us the series code of S= 4n+4 and k = 2n-2 and the F₂ molecule, the code is M-2-2-14 from which S = 2n+6 and k = 2n-3.

In the case of transition metal carbonyl clusters, E represents the sum of eighteen electron sets and V the sum of valence electrons from the metal atoms and the ligands. The empirical formula generates the cluster k values and some of these are given in Table 2. It was also observed that the cluster such as Os₆(CO)₁₈, the k value was 12 and the number of valence electrons 84. Hence its code is M-6-12-84. Clearly V =14n and k = 2n. The same situation prevails for Os₇H₂(CO)₂₀ where k = 14 and V = 98. Hence the code is M-7-14-98. In this case as in the previous complex, S = 14n = 98 and k =2n = 14. Thus, these two clusters belong to the same series. Furthermore, both these clusters are mono-capped, the former the capping is on a trigonalbipyramid geometry [M-5] while latter the capping is on an octahedral geometry. Using the 14n as a baseline, the other clusters series were derived. For example, Mn₂(CO)₁₀; the code is M-2-1-34. This corresponds to the series S = 14n+6 and k = 2n-3. For the cluster Ir₄(CO)₁₂ , k = 6 and V = 60. Hence the code is M-4-6-60 where S = 14n + 4 and k= 2n-2. The series of other clusters for the metal complexes and main group elements were derived and selected ones are given in Tables 4 and 5 and the general one is Table 3 which can be used to classify a given cluster into closo, nido, arachno and hypho or any other type.

Classification of Selected Clusters of the Main Group Elements

The examples for illustration are taken from the article on Polyhedral Skeletal Electron Theory on the website¹⁰ and the 4n rule will be applied. The first one is Pb₁₀²^―; n = 10, 4n = 40 and V = 42. Hence the series is of the type S = 4n+2. This belongs to CLOSO series and k= 2n-1 = 19. Since this is a closo cluster, it will correspond to B₁₀H₁₀²^― (k= 19). The S₄²⁺ cluster; n = 4, 4n = 16 and V= 22. Thus S = 4n+6 placing the cluster into ARACHNO series with k = 2n-3 = 5. This implies the shape of a square with 5 bonds. The fifth one is probably a delocalized bond giving a shape of a regular square. The B₅H₅⁴^― cluster; n = 5, 4n = 20, V = 24 and hence S = 4n +4 . This cluster belongs to NIDO series with k = 2n-2 = 8. This characteristic to a square pyramid shape. The carborane cluster C₂B₇H₁₃; n = 9, 4n = 36 and V = 42. Hence, S = 4n+6. This is an ARACHNO series with k =2n-3 = 15. The clusterC₂B₇H₁₃ corresponds to (BH)₉(H)₆ = B₉H₁₅borane. The P₄ molecule has n =4, 4n = 16 and V= 20. Therefore S = 4n + 4. This places the cluster into the NIDO category with k = 2n-2 = 6. This is a characteristic of a tetrahedral geometry. Its cluster code is M-4-6-20. If 10n electrons(40) are added to the valence electrons the code becomes M-4-6-60. This is the same as Ir₄(CO)₁₂ whose skeletal atoms also have got a tetrahedral shape. The P₄S₃ cluster; n = 7 and 4n = 28 and V= 38. Hence S = 4n+10 with k = 2n-5 = 9. This corresponds to a modification of the P₄ geometry by inserting 3 S atoms into three of the six tetrahedral bonds and thus creating the 9 linkages. The last one is the hydrocarbon C₆H₁₄; n = 6, 4n = 24 and V =38. Therefore S = 4n +14 and k = 2n -7 = 5. This value gives rise to some hydrocarbons isomers some of which are presented in Scheme 6.

schem6

Conclusion

The transition metal carbonyl clusters can be classified using the 14n rule where n is the number of skeletal atoms in the cluster. The 14n is used as a basis upon which the type of cluster series of a given complex is deduced. The cluster series in Table 3 were derived using the cluster number k obtained froman empirical formula explained above using the knowledge of 18 electron rule and cluster valence electrons. The cluster number can also be calculated from the cluster series of the complex. Arising from the simplicity of the 14n rule in categorizing a cluster, a large number of clusters were analyzed. The method also revealed the existence of nuclear inner core closo clusters in some of the large clusters. For instance, the method indicated that the cluster Ni₃₈Pt₆(CO)₄₈H⁵^―, with a code C³⁸C[M-6] has an octahedral nuclear cluster inner core surrounded by 38 cluster atoms in a form of capping. A cluster code notation of clapping series has thus been introduced. Furthermore, it is exceedingly fascinating to discover that in this complex the octahedral nucleus comprised of the six platinum atoms. In such clusters the central inner core acted as a nucleus around which other atoms clustered in the form of capping. However there were some clusters whose inner core nuclei could not be defined by this method. The use of 14n rule or 4n rule to categorize a given cluster of a transition metal carbonyl or main group element is easy, smooth and versatile. The empirical formula k = ½ (E-V), the 4n and 14n rules as well as the cluster series were extracted from the lurking relationship existing between the valence electrons, the number of skeletal elements and the octet and eighteen electron rules. This article highly underpins the powerful insights of Lewis’s octet rule¹⁴and Langmuir’s 18 electron rule¹⁵ of more than ninety years ago.

References

Wade, K. ,J. Chem. Soc., Dalton, 1971, 792-793.
Mingos, D. M. P., Nature Physical Science, 1972, 236, 99-102.
Jemmis, E. D., J. Am. Chem. Soc., 2001, 123(18), 4313-4323.
Jemmis, E. D., Balakrishnarajan, M. M.,Pattath, D., Chem. Rev, . 2002, 102(1), 93-144.
King, R. B., Inorg. ChimicaActa, 1986, 116, 99-107.
Teo, B. K., Longoni,G., Chung, F. R. K., Inorg. Chem., 1984, 23, 1257-1266.
Zanello, P. in ‘Unusual Structures and Physical Properties’, Edited by Glein, M.,Gielen, M, Willen, R., Wrackmeyer, John Wiley and Sons, New York, 2002.
Zanello, P., Rossi, F., PortugaliaeElectrochimicaActa, 2011, 29(5), 309-327.
Belyakova, O., A., Slovokhotov, Y. L., Russian Chemical Bulletin, International Edition, 2003, 52(11), 1-29.
En.wikipedia.org/wiki/Polyhedral_skeletal_electron_pair_theory, downloaded 11-05-2015.
Kiremire, E. M., Orient. J. Chem., 2015, 31(1), 387-392.
Kiremire, E. M., Orient. J. Chem., 2014, 30(4), 1475-1485.
Critchley, G., Dyson, P.J., Johnson, B. F. G., McIndoe, J. S., O’Reilly, R. K., Langridge-Smith, P. R. R., Organometallics, 1999, 18, 4.090-4097.
Langmuir, I., J. Am. Chem. Soc., 1916, 38(4), 762-785.
Jensen, W. B., J. Chem. Educ., 2005, 82, 28-29

This work is licensed under a Creative Commons Attribution 4.0 International License.

Classification of Transition Metal Carbonyl Clusters Using the 14n Rule Derived from Number Theory

Links

Contact Us

Google Page Rank

License