Numerical Assignment of Shapes And Symmetries of Borane Molecules and Ions
Enos M.R. Kiremire*, Likius S. Daniel, and Philipus Hishimone
Department of Chemistry and Biochemistry, University of Namibia, Private Bag 13301, Windhoek, Namibia
DOI : http://dx.doi.org/10.13005/ojc/300302
Article Received on :
Article Accepted on :
Article Published : 18 Sep 2014
The borane chemistry has continued to expand since the beginning of the twentieth century. It has deeply penetrated into the other fields such as organic chemistry, inorganic chemistry, organo metallic chemistry, catalysis, and medicinal fields. Yet some of the average chemists or chemists at an undergraduate or even postgraduate levels find it a challenge to explain the structures of simple boranes. In this article, we present an empirical formula that can be utilized to deduce geometrical shapes of simplesboranes. The formula is so versatile as to be applied to deduce the Lewis structures of simple molecules and ions, inorganic clusters of main group elements, the carbonyl clusters of transition metal complexes as well as carboranes symmetries and hydrocarbons. In the case of hydrocarbons, it is useful in generating isomers of a given hydrocarbon. It is hoped that the formula will be extended to explain the structures or shapes and symmetries of large clusters and to systems which may not obey the octet or eighteen electron rule.
KEYWORDS:Numerical Assignment; chemistry; simplesboranes
Download this article as:| Copy the following to cite this article: Kiremire E. M. R. , Daniel L. S., Hishimone P, Tripathy M. Numerical Assignment of Shapes And Symmetries of Borane Molecules and Ions. Orient J Chem 2014;30(3). |
| Copy the following to cite this URL: Kiremire E. M. R. , Daniel L. S., Hishimone P, Tripathy M. Numerical Assignment of Shapes And Symmetries of Borane Molecules and Ions. Orient J Chem 2014;30(3). Available from: http://www.orientjchem.org/?p=4754 |
INTRODUCTION
Borane molecules and ions have fastinated scientists for a long time since the beginning of 20th century1-2. Unlike hydrocarbons, boranes do not occur in nature, that is, they are generated synthetically3. As it is well known that hydrocarbons are vitally important as they play a crucial role in the provision of energy and many industrial and pharmaceutical chemicals and materials4. It is not surprising that boranes have undergone intense investigations for possible utilization in the production of energy as well as in the potential medicalapplications4-6.Furthermore, the chemistry of boranes has expanded into other fields of chemistry such as organic and organometallic chemistry7. The synthetic techniques developed, bonding as well as shapes and symmetries of neutral boranes and borane ions have challenged great chemists and continue to do so8-15.
It is interesting to note that the elements of the periodic table follow an arithmetical progression. This progression may be presented by a simple formula below.
Z = a1 + (n-1)d
where Z= atomic number of an element in the periodic table, a1 = 1 , the first element (H) , d =1; the difference between successive elements and n is the nth element.
The range of periodic table elements has considerably been expanded with the production of synthetic elements ranging from Z = 99 to the current 118 element. From 2000 to 2010, five artificial elements were discovered ( Z = 113, 115, 116, 117 and 118).
In this paper, we present the assignment of numbers to shapes and symmetries of molecules and ions of boranes. This procedure has been presented earlier16-17. However, in this article the empirical formula has been refined to probe detailed linkages including those of the hydrogen atom linkages of the boranes. The numbers are generated from an Empirical Formula given by
k = ½ (E-V) k=is a representative number of bonds, linkages or shape and symmetry of a given molecular formula of neutral borane, ion or carborane; E = the sum of octet (8) electrons for the atoms assumed to obey the octet rule in the molecular formula.; V = the sum of the valence electrons of all the atoms in the molecule or cluster.
The empirical formula is readily applicable to transition metal carbonyl complexes with metal- metal bonds and main group clusters which obey 18 and 8 electron rules respectively[ ]. In the case of H atom in a covalent bonding obeys the 2 electron rule. When the 2, 8 and 18 electron rules when closely scrutinized, it is discerned that these rules have their foundations in the noble gas configurations. In the case of boranes and hydrocarbons to be discussed in another paper, the empirical formula has been refined to include not only the skeletal or linkages but all number the bonds within the formula of the molecule or ion. In view of the rapid expansion of the borane chemistry including potential application, it is important to find a simple method of deducing the structures of boranes at least the simple ones so that they are reasonably explicable at an average or junior chemist. This empirical formula is an attempt in that direction.
Simple examples for illustration
Let us consider simple molecules and ions first.
Take the case of C2molecule. When the empirical formula is applied, we find that it has a quadruple bond rather than a double bond as predicted by molecular orbital theory. According to the formula, k = ½ (E-V), each of the C atom will obey the octet rule hence E= 2×8 = 16, and the sum of valence electrons V = 2×4 = 8. Hence k = ½ (16-8) = 4. This result is quite interesting in the sense that recently, a quadruple bond for C2 has been found [ ]. For NO+ ion, E = 5+6-1 =10. Hence k = 3. Similarly, CN– (k =3), NO– (k =2), CO2 (k =4), HCN( E = 2+8×2 =18, V = 1+4+5 =10 and k = 4), N2H4 (E = 4×2+2×8 = 24, V =5×2+4 =14 and k =5) and CH4 ( E = 8 + 4×2 = 16, V = 4 +4 = 8 and k = 4). The 16, =distribution of bonds of k values such the atoms obey the 2 or 8 electron rule as the case may be for selected molecules/ions is illustrated in the sketch 1 below consistent with the known shapes.
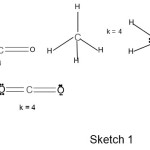 |
Sketch 1 Click here to View Sketch |
As4 cluster
Arsenic has five valence electrons and if each is surrounded by 8 electrons, then E = 4×8 =32, and V= 5×4 =20. Hence, k= ½ (32-20) = 6. This means the four atoms are connected by 6 linkages. This is consistent with a tetrahedral geometry, Td (Fig. 1).
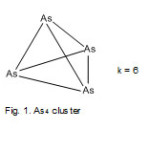 |
Figure 1 Click here to View Figure |
Bi5?3+ cluster
In this case, the parameters of the empirical formula have the values E= 5×8 =40, V =5×5-3 =22 and k = 9. The 9 linkages are consistent with a trigonal bipyramid geometry ( D3h).
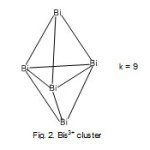 |
Figure 2 Click here to View Figure |
C2H4 molecule
In the case of C2H4, each of the two C atoms obeys the octet rule. The skeletal bonds linking up the two atoms are given by k1 = ½ (16-12) = 2. If the H atoms are taken into account, and that each H atom obeys the 2 electron rule, then the total linkages(bonds) are given by k2 = ½ (E2 –V); E2 = 2×8+4×2= 24, V= 12. Hence, k2 = ½ (24-12) =6. Since k1 = 2, then k2 – k1 = 4. The 4 linkages will be for the 4 hydrogen atoms to the carbon atoms.
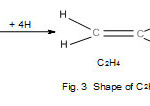 |
Figure 3 Click here to View Figure |
k2 = 6 means that all the 6 bonds linking up the 6 planar atoms in C2H4 are identified by the k2 value.
B2H6 molecule
The bonding and structure of diborane became very controversial when the interest in the borane compounds was ignited by A. Stock who opened the door into the fertile field and many others followed [ ]. The shape of B2H6 was confirmed to be a doubly bridged one almost similar to that of C2H4 except that the bridges referred to as banana bonds were perpendicular to the plane of B2H4 fragment.
Applying the empirical formula k = ½ (E-V) to the B2H6 molecule for the two B atoms excluding the H atoms,
E1 = 2×8 =16, V = 2×3+6×1 = 12. Hence k1 = ½ (16-12) = 2. In principle, the two boron atoms in B2H6 will linked by a double bond as in C2H4. The skeletal bonds are indicated in Fig. 4. In order for the boron atoms to obey the octet rule, each B atom must have two additional bonds or linkages for 4 hydrogen atoms. But in order to comply with the octet rule requirement, the 2 additional H atoms must donate electrons to the skeletal bonds. The sketch is given in Fig. 4.
The value of k2 is obtained from E2 = 2×8+6×2 = 28, and V= 2×3+6×1 = 12. This gives a calculated k2 = ½ (28-12)= 8. This corresponds to the total linkages of 8 as seen from Fig. 4.
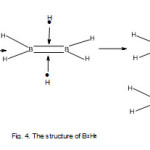 |
Figure 4 Click here to View Figure |
The k2 value gives all the total linkages including the bridges. Each bridge taken as equivalent to two linkages. It is quite clear from the sketch in Fig. 4 that there is resemblance to that of C2H4 shown in Fig. 3. Thus, a (BH) fragment can regarded as equivalent to a (C) atom. That is, BH = C as these are isoelectronic. This also means that we can regard BH3 to be equivalent to (BH)H2 = CH2. Hence, 2CH2 = 2(BH)H2. This makes visual sense for sketches of C2H4 in Fig. 3 and B2H6 in Fig. 4.
Deriving the shapes of boranes using k1 and k2 values B2H7?― ion (k1 =1, k2 = 8 )
The k values imply that the two boron atoms are connected by a bridge(2 linkages) and each B atom will have three terminal hydrogens( Fig. 5).
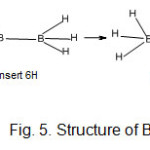 |
Fig5: Structure of B2H7 Click here to View Figure |
The sketch of B2H7⏋― is is oelectronic to that of C2H6 which has a similar resemblance
B3H8?― ion (k1 =3, k2 = 11)
The value of k1 = 3 for B3H8⏋― ion implies that the three boron atoms are linked by three bonds to form a trigonal planar geometry. In order for each B atom to obey the octet rule, two terminal linkages have to be introduced. This needs 6 B-H terminal bonds leaving 2 hydrogen atoms to be inserted into bridges. The final geometry is shown in Fig. 6.
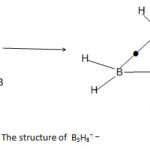 |
Fig6: The structure of B3H8⏋― Click here to View Figure |
After insertion of the two bridges, the total number of linkages corresponds to k2 = 11.
B4H10 molecule ( k1 = 5, k2 = 15 )
One possible geometry consistent with these k-values is shown in fig.
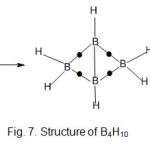 |
Fig7: Structure of B4H10 Click here to View Figure |
Influence of varying of H atoms and Charge on the geometry of Bn Fragment
The variation of the number of H atoms and the charge on the Bn fragment of the cluster has an influence on the cluster geometry. This is illustrated by the variation in the structure of B4fragment in the clusters shown in the following fig 8 B4H9?― cluster (k1 = 5, k2 = 14) B4H8 cluster (k1 = 6, k2 = 14)
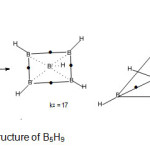 |
Fig8: B4H7⏋― cluster (k1 = 6, k2 = 13) Click here to View Figure |
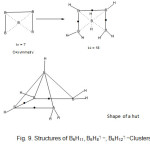 |
Fig9: B4H4⏋2― cluster (k1 = 7, k2 = 11) Click here to View Figure |
B4H7?― cluster (k1 = 6, k2 = 13) B4H4?2― cluster (k1 = 7, k2 = 11)
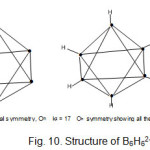 |
Figure 10 Click here to View Figure |
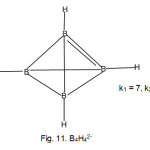 |
Figure 11 Click here to View Figure |
B4H4?4― cluster (k1 = 6, k2 = 13)
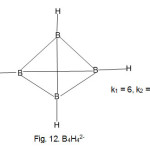 |
Figure 12 Click here to View Figure |
B5H9 molecule (k1 = 8 , k2 = 17 )
The hydride B5H11( k1 = 8 ) implies a square pyramid skeleton (C4v symmetry). When bridges and terminal bonds are included, the total linkages become 17. The plausible shapes are shown in Fig. 8.
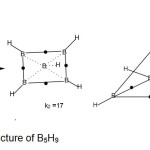 |
Figure 8 B Click here to View Figure |
B5H11 borohydride (k1 = 7, k2 =18)
The skeletal geometry of B5H11 (k1 = 7) may be considered a derivative of that of B5H11 (k1 = 8) with one base side removed. To move from k1 = 7 to k2 = 18) bridges and terminal bonds have to be included. This is shown in Fig. 9.
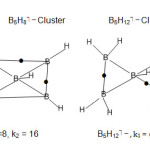 |
Fig9: Structures of B5H11, B5H8⏋―, B5H12⏋―Clusters |
B6H6?2― cluster ion(k1 = 11, k2 = 17= 11+6)
B6H6?2― cluster ion has k1 value of 11 and k2 value of 17. The difference between k2 and k1 is 6. This represents the six B-H terminal bonds for this closo system. The k value of 11 for six skeletal atoms is characteristic of an octahedral skeletal symmetry (Oh)(Fig. 10.). It is interesting to note that whereas the k1values of B4H4⏋2― (k1 = 6 ) and B5H5⏋2― (k1 = 9 ) correspond to the number of total skeletal linkages, whereas in B6H6⏋2― (k1 = 11) octahedral skeletal symmetry, this is not the case. The k2 = 17 represents k1 = 11 for skeletal symmetry plus 6 for hydrogen bond linkages
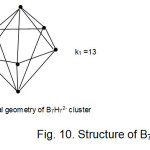 |
Figure 10 Click here to View Figure |
B7H7?2― cluster ion
The B7H7?2― cluster ion has a characteristic k1 value of 13 and k2 of 20. It is found to adopt a pentagonal bipyramid skeletal geometry (D5h). This is shown in Fig. 11.
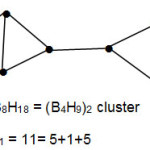 |
Figure 10 C Click here to View Figure |
Closo Boranes
The closoboranes have characteristic k1 values which have number series that begins with k1 = 3 for B2H2?2―, B3H3?2― (k1 =5 ), B4H4?2―(k1 =7), B5H5?2―(k1 = 9), B6H6⏋2―(k1 = 11), B7H7⏋2―(k1 =13),B8H8?2―(k1 = 15), B9H9?2―(k1=17), B10H10?2―(k1 =19),B11H11?2―(k1 = 21), and B12H12?2―(k1 =23). The k1 values form a series of odd numbers for the closo series.
The conjucto clusters
The empirical formula could be extended to the interpretation of geometries of large clusters. Take the example of B8H18 = (B4H9)2 cluster.This cluster has k1 = 11. This can be split into 5+1+5. A plausible isomer consistent with this is given below.
B10H16 (k1 =17).
This can be separated into 8+1+8 units. The k1 = 8 is a square pyramid of B5H8. This means that two fragments of B5H8 are linked up by a single bond. The shape of B10H16 is shown below. This is an example of a bridged fragments or skeletal units of boranes.
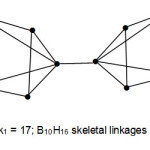 |
Figure 10 D Click here to View Figure |
Closo Series
The closoboranes are given by the formula BnHn?2-. The k1 and k2 values of the closo series are given in Table 1.
Table 1. The k1 and k2 values for Selected Closo Boranes BnHn?2-
| n | k1 | k2 |
| 2 | 3 | 5 |
| 3 | 5 | 8 |
| 4 | 7 | 11 |
| 5 | 9 | 14 |
| 6 | 11 | 17 |
| 7 | 13 | 20 |
| 8 | 15 | 23 |
| 9 | 17 | 26 |
| 10 | 19 | 29 |
| 11 | 21 | 32 |
| 12 | 23 | 35 |
| 13 | 25 | 38 |
| 14 | 27 | 41 |
| 15 | 29 | 44 |
| 16 | 31 | 47 |
| 17 | 33 | 50 |
| 18 | 35 | 53 |
| 19 | 37 | 56 |
| 20 | 39 | 59 |
It is quite clear from Table 1 that the k values form arithmetical series. The series for k1 values follow the pattern given by T1 = an + (n-1)d; a1 = 3, d =2, and T1 = nth value of k1. On the other hand for k2 series is given by T2 = an + (n-1)d; a1 = 5 and d = 3 and T2 = nth value of k2.
The k1 and k2 values of selected neutral and ionic boranes from B2 to B12 boron-based systems are given in Table 2. Table 3 gives the linkage of k1 and k2 values of the closo series to vertices and shapes of known closo borane ions such as B5H5?2―, B5H5⏋2―, andB7H7?2―.
Table 2: The k values of Selected Boranes
| Molecule/Ion | E1 | V | k1 = ½ (E1 –V) | E2 | k2 =½ (E2 – V) |
| k2* = k1 + n | |||||
| B2H6 | 16 | 12 | 2 | 28 | 8 |
| B2H7⏋― | 16 | 14 | 1 | 30 | 8 |
| B3H8⏋― | 24 | 18 | 3 | 40 | 11 |
| B3H9 | 24 | 18 | 3 | 42 | 12 |
| B4H4⏋4― | 32 | 20 | 6 | 40 | 10 |
| B4H7⏋― | 32 | 20 | 6 | 46 | 13 |
| B4H8 | 32 | 20 | 6 | 48 | 14 |
| B4H9⏋― | 32 | 22 | 5 | 50 | 14 |
| B4H10 | 32 | 22 | 5 | 52 | 15 |
| B5H8⏋― | 40 | 24 | 8 | 56 | 16 |
| B5H9 | 40 | 24 | 8 | 58 | 17 |
| B5H11 | 40 | 26 | 7 | 62 | 18 |
| B5H10⏋― | 40 | 62 | 7 | 60 | 17 |
| B6H9⏋― | 48 | 28 | 10 | 66 | 19 |
| B6H10 | 48 | 28 | 10 | 68 | 20 |
| B6H11⏋+ | 48 | 28 | 10 | 70 | 21 |
| B6H11⏋― | 48 | 30 | 9 | 70 | 20 |
| B7H11 | 56 | 32 | 12 | 78 | 23 |
| B8H12 | 64 | 36 | 14 | 88 | 26 |
| B8H14 | 64 | 38 | 13 | 92 | 27 |
| B9H13 | 72 | 40 | 16 | 98 | 29 |
| B9H15 | 72 | 42 | 15 | 102 | 30 |
| B9H12⏋― | 72 | 40 | 16 | 96 | 28 |
| B9H14⏋― | 72 | 42 | 15 | 94 | 26 |
| B10H14 | 80 | 44 | 18 | 108 | 32 |
| B10H16 | 80 | 46 | 17 | 112 | 33 |
| *n = number of H atoms on cluster. | |||||
Table 3: The k values of Closo systems from n = 2 to 12 and possible Shapes/
| BnHn⏋2―Ion | E1 | V | k1 = ½ (E1 –V) | E2 | k2 =½ (E2 – V) | N = ½ (k1+1) | Possible geometry |
| Closo system | Vertices | ||||||
| B2H2⏋2― | 16 | 10 | 3 | 20 | 5 | 2 | |
| B3H3⏋2― | 24 | 14 | 5 | 30 | 8 | 3 | |
| B4H4⏋2― | 32 | 18 | 7 | 40 | 11 | 4 | |
| B5H5⏋2― | 40 | 22 | 9 | 50 | 14 | 5 | Trigonal bipyramid |
| B6H6⏋2― | 48 | 26 | 11 | 60 | 17 | 6 | Octahedral |
| B7H7⏋2― | 56 | 30 | 13 | 70 | 20 | 7 | Pentagonal bipyramid |
| B8H8⏋2― | 64 | 34 | 15 | 80 | 23 | 8 | Dodecahedron |
| B9H9⏋2― | 72 | 38 | 17 | 90 | 26 | 9 | Tricapped trigonal prism |
| B10H10⏋2― | 80 | 42 | 19 | 100 | 29 | 10 | Bicapped square antiprism |
| B11H11⏋2― | 88 | 46 | 21 | 110 | 32 | 11 | Octadecahedron |
| B12H12⏋2― | 96 | 50 | 23 | 120 | 35 | 12 | Icosahedron |
CONCLUSION
The k values of simple neutral and ionic boranes can be used as guide to explain the shapes and symmetries of the same. Furthermore, they can act as an identity for characteristic shapes of molecules and ions especially the closo systems. For instance, k1 = 11 is characteristic of an octahedral geometry as in the case of B6H6⏋― or k1 =13 for pentagonal bipyramid for B7H7⏋2―. The empirical formula k = ½ (E-V) is versatile as it can be utilized to sketch Lewis shapes of simple ions and molecules as well as clusters of simples molecules and ions of the main group elements. It can be extended to explain the shapes of simple transition metal clusters containing carbonyl ligands. The empirical formula is also applicable to carboranes since they are related to boranes. It is hoped that the empirical formula will find some applications in more complex molecular systems where the 2, 8 and 18 electron rules are obeyed.
References
- Stock, A., Hydrides of Boron and Silicon, Cornell University Press. Ithaca, New York, (1933).
- Fox, M. A.; Wade, A. Pure and Appl. Chem.,2003, 75(9), 1315-1323 and references therein
- http://en.wikipedia.org/wiki ; downloaded 20-07-2014.
- Zhang, X. B.; Hans, S.; Yan, J. M.; Chandra, M.; Shioyana, H.; Yasuda,K.; Kariyama, N.;Kobayashi,T.; Xu,Q. Journal of Power Sources, 2007,168, 167-171.
- Hawthorne, M. F.;Varadarajan, A.; Knobler, C. R.; Chakrarti, S.;Paxton, R. J; Beatty, B. G.; Curtis, F. L. J. Am. Chem. Soc.1990, 112(13), 5365-5366
- Hawthorne, M. F., and Maderna, A. Chem. Rev. 1999, 99, 3421-3434.
- Sneddon, L. G. Pure and Appl. Chem.1987, 59(7), 837-846.
- Hall, C.; Thakaran, P.; Hallock, J.; Cleveland,C.; Jefferson, M. Nature 2003,426, 318-322.
- Wade, A. Adv. Inorg. Chem. Radiochem. 1976, 18, 1-66.
- Mingos, D. M. P. Acc. Chem. Res. 1984, 17(9), 311-319.
- Shore, S. G. Pure and Appl. Chem. 1977, 49(6), 717-732.
- McGlinchey, M. J.; Hopf, H. Beilstein J. Org. Chem.2011, 7. 222-233.
- Jemmis, E. D.; Balakrishnarajan, M. M.; Pancharatna, P. D. J. Am., Chem. Soc.2001, 123(18), 4313-4323.
- Welch, A., J. Chem. Comm. 2013, 49, 3615-3616
- Kiremire, E. M. R. Oriental J. Chem. 2007, 32(2), 809-812.
- Kiremire, E. M. R.; Kiremire, E. B. B. Materials Science Research India 2007, 4(1), 09-18.

This work is licensed under a Creative Commons Attribution 4.0 International License.









