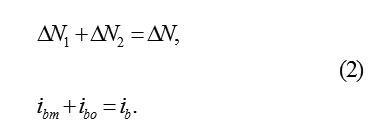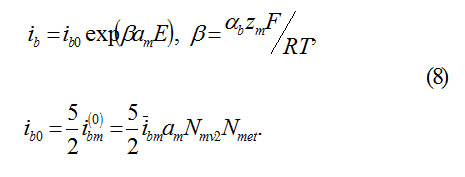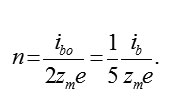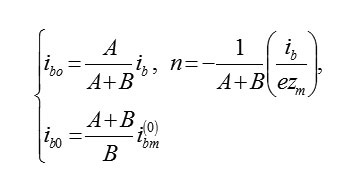A Physical Model of the Interphase Boundary of the Passivating Layer on the Metal in the Electrolyte Solutions

Introduction

The mechanism of processes on the interphase boundary of the passivating oxide layer PL has a fundamental value, whereas, the properties of the passivating layer are determined by them.In this paper a consistent model of the boundary metal-oxide MO is presented.

General stationary laws

On the interphase boundary of metal with PL, the continuous dissolutionof metal occurs.it disappears consecutively monolayer after a monolayer and the cells of oxide occupy its place. if at time the layer of metal of thickness disappears, then the plane MO displaces in its side with the speed , equals

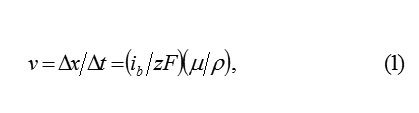
where i_b– total dissolution current; μp-  the molar mass and density.The thickness of the oxide layerΔ_ok substituting Δ_M for the same timeΔ_t , is also equal Δ_x . let us designate a quantity of ions in the initial Δ_M layer of metal and its substituted layer of oxide Δ_ok by and ΔN₁ respectively. It is obvious, that ΔN₁ < _ΔN, since the specific volumes, according to the metal ion, in Δ_M and Δ_ok are different. Consequently, only ions in  ΔN₁ a layer Δ_M in volved in the formation of oxide .  Δ_ok The remaining part, equal , ΔN2 = ΔN ΔN_1, considered to be excess and must leave into the solution through the boundary MO and PL. Therefore, the balance of space in the layer of metal and the oxide is observed.considered to be excess and must leave into the solution through the boundary MO and PL. Therefore, the balance of space in the layer of metal Δ_M  and the oxide Δ_ok  is observed.Thus the surface MO serves as the source of ions  M^Z+_ok , and in the passivating layer, their intensive transfer by the mechanism of hopping migration in the strong electric field   should be occurred. Accordingly, the total current  of the dissolution of metal is divided into the transfer current  of the ions through the boundary MO in PL and the current  of oxide formation on this boundary (subscripts indicate: b- boundary, m- metal, o- oxygen; the current i_bo determines a quantity of metal ions, which in 1cm³ every second are connected in the layer Δ_M with oxygen), such as

 

The subsequent analysis confirms this conclusion.  The total current i_b must be equal

 

 

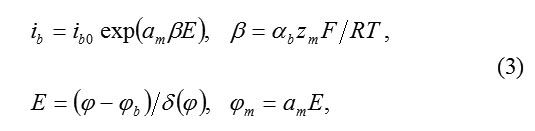
Where a_m – interatomic distance in the cationic sublattice, α_b transfer coefficient on the boundary MO.

Equation(3) assumes, that an ion M,passing into the state of anion M^Z+_ok must overcome a potential jump Φ_{M= αM}E. Thus, the barrier of transition decreases to ΔW_M= α_bz_MΦ_M The constant i_b0 of transition speed is determined from the independent temperature measurements ( for Fe, for example, )i_bo ˜10^-10A/cm²

The total current i_b is the fundamental characteristic of stationary processes on the interphase boundary MO, and the micro scheme of the formation of cells M₂O₃ are ambiguous. They must consider a difference between the interatomic distances and the angular directions in the lattices of metal and oxide, and require the use of probabilistic methods for describing regrouping particles.

Further, it is interesting to detail a physical situation on a surface MO to calculate the currents  i_bm,  i_bo and the ratio between the values ΔN₁  and ΔN₂ . For this purpose let us proceed from general consideration to the specific models of processes on the boundary MO. The most simple and real vacancy model is presented below. It allows to open a better physical sense of the relations (3).

The vacancy model of MO boundary

Vacancy model proceeds from the idea about the fact that, for forming the new cell M₂O₃  , three ions O² _-ok from the passivating layer must penetrate in the boundary mono layer of metal. This requires the presence of  three vacancies V_m  in it, which can arise only as a result of previous transition in the passivating layer of three ions of metal. These ions fill three vacancies Vom in the cation’s sublattice of oxide.The transition scheme

(V_om – vacancy in a metallicsublattice of oxide, V_m – vacancy in the boundary layer of the metal ΔM  )

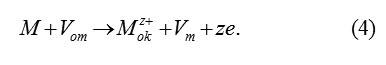
Transition (4) serves as the necessary condition for the subsequent penetration into the layer ΔM  of oxygen ions

Where V_ok– vacancy in the oxygen sub lattice in place passed into the metal O^2-_Ok ion.

The opposite reactions (4), (5)- appear basic in the vacancy model. It is obvious, that the surface MO serves as a drain of cationic vacancy V_om , brought by their diffusive flow j_mv from solution. Simultaneously, it is the source of the vacancies V_ok, which are discharged into the solution by their flow j_ov. Flows j_mv and j_ov appear, of course, as a result of the motion of ions M^z+_ok and O2^–_ok in the passivating layer by the mechanism of hopping migration in the strong field.

The transformation of vacancies and their flows occurs on the surface MO by the scheme.

In this transformation, the vacancies V_m are mediators, which connect processes (4) and (5). Their total quantity R  is determined by the withdrawal of metal ions  M and penetrationin metal of the oxygen ions O2^–_ok, i.e. the relations of the speeds (4) and (5).In the stationary mode, the value of  R is invariable ( see below).

The speeds of formation of oxide and cation transfer through the boundaryMO.

Thus, processes On the boundary MO are characterized by the currents (speeds) i_bm, I_bo of reactions (4), (5) and by the total current i_bof the metal dissolution.It is measured, and is primary value, and its determination (3) can be called extra-model. The calculation of currents  i_bm, I_bo depends on model presentations. let us examine these values.

1) Transition current i_bm of ions M in the passivating layer and their further transfer to the solution depends on the electric field E and the boundary concentration a_mN_mv2 of vacancies V_om. Indeed, for transition into the passivating layer according to the scheme (4), ions M must cross the plane MO and move away from it on interatomic distance a_m of a cationic sublattice, having overcome potential jump Φ_m =a_mE. Transition barrier is reduced on ΔW_m=α_bz_ma_mE, its probability is proportional to a quantity of vacant places, i.e., the concentration a_mN_mv2 of vacancies V_m. As a whole the speed (4) is equal

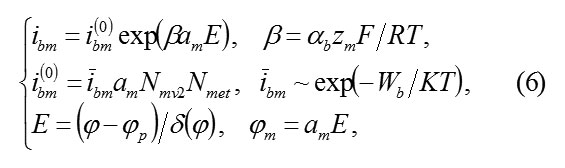
α_b– transfer coefficient, N_met – concentration of atoms in metal,i_bm– speed constant of reaction.

2) The current  i_bo of ions M, which form oxide MO_z/2 according to the reaction (5) , represents the speed of oxide formation on the Boundary MO.let us take it equal to (i_bo – constant of speed, reverse current  is neglected)

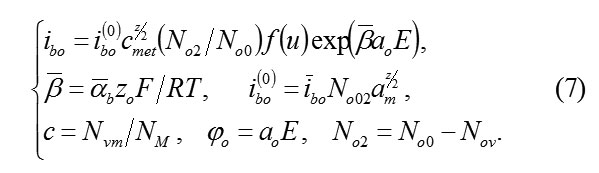
In the system (7), the dependence of current  i_bo on the field E, the concentration c_met , the vacancies V_m  and the probabilistic factor f(u) are taken into account. the influence of field  E is regulated by the value of transfer coefficient α_b , and it is connected with the fact, that for the  penetration  into the metal through the plane MO, ion O^2-_ok   must dislocate in the anion sublattice to the interatomic distance a₀ , overcoming the potential jump φ₀=a₀E .In this case, the barrier of penetration is reduced to the value ΔW₀=α_bz₀a₀E. Influence on current i_bo  of concentration c_met considered with the fact, that without vacancies V_m, penetration can’t occur (see (5)).

The Probability factor f(u) in (7) takes into account the specific mechanism of formation of cells MO_z/2. If the penetration of ions O^2-_ok and the structuring of cells occur in parallel, then it is not possible to exclude the deceleration necessary of regrouping of particles. The micro schemes of these processes can be different and random. Their possible influence on the speed of formation of oxide is described by probabilistic factorf(u) in (7). Its calculation is an autonomous task.

If the penetration of ions O^2-_ok is limited and it is weakly dependent on the subsequent structuring, then f(u)=1. Within the limit of the passivating layer it can consist of the partially structure systems complexes M₂O₃ , the speed of formation of which is determined by (7) at f(u)=1. Structuring depends, in particular, on the noncoincidence of interatomic distances and angular orientations in the lattices of metal and oxide.

Transfer coefficients α_b and β_b=1-α_b and in (6) and (7) characterize asymmetry barrier W, which overcome by ions during their motion on the units of crystal lattice in the direct and opposite directions. Depending on α and β, how much an electric field changes barrier W. In the case of an isotropic gomogennmedium α_b~ β_{b ~ ½} . However, in a thin passivating layer on the strange base layer, these values α_b and β_b are not proved. Furthermore, the current values α_b , βb in the volume of the passivating layer, and its more disordered boundaries may differ, i.e they depend on coordinate system. Apparently, in this respect, the boundary MO is isolated, on which exactlyα= α_b,β= β_b. Then the jumps of the potential φ_m and φ₀ overcome by ions M and O2^–_ok upon transition through the plane MO are equal respectively to φ_m=a_mE and φ₀=a₀E, Barriers(4) in the Boundary MO are reduced on ΔW_m=α_bz_mφ_m and ΔW₀=α_bz₀φ₀ . All this are taken into account in (6) and (7).

Using (6), (7) it is possible to calculate stationary concentration of vacancies. Actually, the withdrawal of ions M and the penetration of ions O2^–_ok are strictly compensated (for example, for formation M₂O₃ , three ions M have to leave metal and three ions O2^–_ok will penetrate in it). for example, for forming , three ions must leave from the metal and three ions will penetrate in it.Therefore, speeds (6) and (7) are identical, i. e. 2/3i_bm = i_b0 and,consequently (excluding small reverse currents)

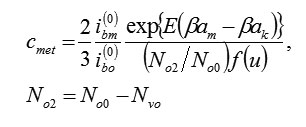
3) total current i_b in the vacancy model is easy to relate with the values i_bm and i_b0 taking into account ,that the dissolution of the metal at the interface MO is faster oxide formation. Actually, according to the presented above, for the appearance of a cell M₂O₃ it is necessary for emergence of a cell, that: a) three ions of metal from a layerΔM passed to PL by the scheme (4), composing the current i_bm; b) three ions O^2-_ok from a passivating layer  enetrated into a layer ΔM according to the scheme (5); c) since, the cell M₂O₃ contains two ions M^z+_ok, then two ions of metal in the layerΔM must be connected with three penetrating ions of oxygen O^2-_ok respectively, to form a complex M₂O₃ and to compose the current i_b0 .

Thus, with the formation of each cell M₂O₃, layer ΔM loses not two, but five ions of metal, from which three prove to be excess.Their departure from the layer ΔM implements balance of space, compensating for the difference in specific volumes for each metal ion in the lattice of a metal oxide.Therefore in the passivating layer the intensive transfer of cations M^z+_ok by the mechanism of hopping migration occurs. The surface MO is their intensive source, concentration N_mv2 of vacancies V_0m in (6) is small, the relation of stationary values of currents m and i_b0 equal 3/2.
The total current is equal to the sum i_b = i_bm + i_b0 = 5/2i_b0 = 5/2i_bm or, accordingly (6),(3)

The current of the formation of oxide is equal i_bo = 2/5i_b. Every second on  1cm²  of the plane MO there is a number of cells M₂O₃ occurs, which at  z_m = 3  be equal

If the stoichiometry of oxide is different than the previous one, then it will change numerical coefficients [2]. In the general case for the cell M_AO_B we have

With the stated of thevacancy model boundaries MO, self processes at the interface with the opposite solution, considered in the following publications.

References

1. Vetter K. Z. // Electrochemist. 1951. V. 55. P.274; 1954. V.58. P. 230; 1955. V. 59. P.67.
2. Popov YU.A. // Electrochemist. 1985. V. 21. P. 1496; 1986. V. 22. P. 762; 1994. V. 30. P. 473.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.