Viscosity of Thorium Soaps

Introduction

Metallic soaps are widely used in industries and allied sciences as catalysts, cosmetics, lubricants, greases, medicines, softeners, flatteners, stabilizers, plasticizers, emulsifiers, surface active agents and waterproofing agents. Therefore, a detailed study of these soaps is required for their great importance in industrial and academic fields. Extensive work has been done on the alkali, alkaline and transition metal soaps but comparatively less work has been done on lanthanide and actinide soaps^1-4. Lanthanum soaps were prepared by Skrylev et al⁵ by the reaction of lanthanum chloride and corresponding salt of fatty acid. Mehrotra et al⁶ prepared the soaps of lanthanum, cerium, praseodymium and neodymium by double decomposition method. Skellon and Andrews⁷ studied the rate of oxidation of fatty acids in the presence of thorium soaps. Volatility and analysis of cerium soaps by treating with oxalic acid was studied by Marwedel⁸. Catalytic activity of cerium, thorium and urany^l soaps was studied by Skellon and Spence⁹ Physico-chemical studies, IR, X-ray and TGA, of thorium and lanthanum soaps in solid state was studied by Mehrotra et al¹⁰ Ultrasonic and conductivity studies of thorium soap solutions have beendone by Mehrotra et al¹¹

The present work solutions have been of density and viscosity of thorium soap solutions in benzene-methanol mixture at different temperatures in order to examine their Micellar behavior and to check the validity of various known equations.

Experimental

All the chemicals used for the preparation of thorium soaps were of AR grade and were purified by standard methods. Thorium soaps were prepared by direct metathesis of the corresponding sodium soaps with the required amount of aqueous solution of thorium nitrate with constant stirring. The precipitated soap was filtered and washed first with distilled water and finally with alcohol. The metal soaps were first dried in an air oven and finally under reduced pressure and further purified by recrystallization.

The viscosity and density of the solutions of thorium soaps were measured by Ostwald’s Viscometer and Pyknometer at different temperatures.

Results and Discussion

Density

The density (r) of the solutions of thorium soaps Lourate and Myristate is determined at different temperatures (40, 50 and 60ºC). The density increases first rapidly and then slowly with the increase in the soap concentration and temperature. The plots of density vs. soap concentration (g mol dm^-3) are characterized by an intersection of two straight lines at a definite soap concentration which corresponds to the critical micelle concentration (CMC) of the soaps, indicating a marked change in the aggregation of the soap molecules at the CMC. The values of the CMC decrease with the chain length of soaps but increase with temperature. The plots of density vs. soap concentration below the CMC have been extrapolated to zero soap concentration and the extrapolated values of the density, r₀ are in agreement with the experimental values of the density of the solvent. The density results have been explained in terms of Root’s equations.

r = r₀ + AC – BC^3/2

Where C is the concentration of the soaps (g mol dm^-3), r and r₀ are the densities of the soap solution and solvent, respectively and the constants A and B refer to the solute-solvent and solute-solute interactions, respectively. The values of the constants A and B have been obtained from the intercept and slope of the plots of (r–r₀)/C vs. C^1/2 below the CMC. The results confirm that the soap-solvent interaction is larger than the solute-solute interaction in dilute soap solution. It is, therefore, concluded that there is a marked increase in the aggregation of the soap molecules and the soap molecules do not show appreciable aggregation below the CMC.

Viscosity

The viscosity (h) of the solutions of thorium soaps (Laurate and Myristate) in benzene-methanol mixture increases with the increase in the soap concentration and chain length of soap and decreases with temperature and vice versa. The plots of the viscosity h vs. the soap concentration are characterized by the intersection of two straight lines at a definite soap concentration which corresponds to the critical micelle concentration. The values of the CMC are affected by the chain length of the anion in the soap. The decrease in the CMC with the length of hydrocarbon chain and increase with temperature may be due to the increase in the stability of the micelles as well as due to the increase in the tendency of aggregation. The plots of the viscosity vs. soap concentration below the CMC have been extrapolated to zero soap concentration and it is observed that the extrapolated values of the viscosity for zero soap concentration are in agreement with the viscosity of pure solvents. This again confirms that the soap molecules do not aggregate to an appreciable extent below the CMC. The viscosity results are satisfactorily explained on the basis of the following equations.

Where, , C, f and h_sp Are molar volume of the soap (dm³ mol^-1), concentration of the soap (g mol dm^-3), interaction coefficient and specific viscosity of the solution, respectively.

The values of the molar volume of the soap have been calculated from the slope of the plots of h_sp vs. C (Einstein’s equation) and from the plots of 1/C vs. 1/[log (h/h₀)] (Vand’s equation) and it is observed that the values obtained from both the equations are in agreement indicating that these equations are applicable to these soap solutions.

Table 1: Values Of Molar Volume,  and Constants A and B Obtained From Different-Equations at Different Temperatures

Soap	Einstein’s eqn.	Vand’s eqn.	Jones-Dole’s eqn.		Root’s eqn.
	x 10-2 dm3 (mol-1)		A	B x 10-2	A	B x 10-2
Temperature 40ºC
Laurate	3.13	3.07	1.00	7.50	23.00	3.00
Myristate	3.20	3.29	1.25	7.69	23.50	3.13
Temperature 50º
Laurate	2.75	2.76	0.75	6.67	29.75	2.50
Myristate	2.91	2.93	1.00	6.78	30.25	2.73
Temperature 60º
Laurate	3.00	3.15	0.25	6.00	40.25	2.50
Myristate	3.20	3.22	0.75	6.11	35.25	2.85

Table 2: Values Of The Cmc (G Mol Dm^-3), C X 10⁴

Soap	Temperatures (ºC)
	40	50	60
Thorium Laurate	6.10	6.30	6.35
Thorium Myristate	6.00	6.20	6.30

 

Conc. Of Soap, CX104(g mol dm-3)	Vicosity at different temperatures (0C)
	40	50	60
Thorium Laurate
1.0	5.22	5.16	5.12
2.0	5.58	5.47	5.40
3.0	5.96	5.82	5.64
4.0	6.34	6.13	5.99
5.0	6.74	6.39	6.20
6.0	7.12	6.77	6.52
7.0	7.60	7.21	6.89
8.0	8.11	7.73	7.40
9.0	8.62	8.67	7.85
10.0	9.00	8.62	8.34
Thorium Myristate
1.0	5.21	5.14	5.09
2.0	5.60	5.47	5.34
3.0	5.97	5.84	5.62
4.0	6.40	6.21	5.95
5.0	6.73	6.50	6.21
6.0	7.12	6.88	6.48
7.0	7.64	7.35	6.90
8.0	8.11	7.89	7.44
9.0	8.64	8.34	7.98
10.0	9.10	9.01	8.47

 

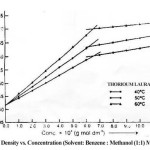Figure 1 Click here to View figure

 

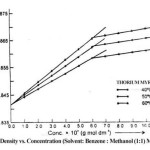Figure 2 Click here to View figure

 

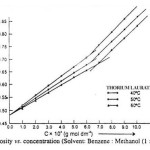Figure 3 Click here to View figure

 

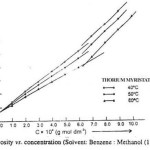Figure 4 Click here to View figure

The applicability of Jones-Dole’s equation was checked by the plots of h_sp/C¹² vs. C^1/2 which are linear below the CMC. The values of coefficients A and B are calculated from the intercept and slope of the plots below the CMC. The values of B are larger than the values of coefficient A, which confirms that the molecules of the soap do not aggregate appreciably below the CMC and there is sulden change in the aggregation above the CMC.

It is, therefore, concluded that the equations of Einstein, Vand and Jones-Dole are applicable to dilute solutions of thorium soaps in benzene-methanol  mixture. The values of the CMC and molar volume of thorium soaps calculate from these equations are in close agreement.

References

1. K.N. Mehrotra, A.S. Gahlaut and M. Sharma, J. Am. Oil Chem. Soc., 63, 157 (1986).
2. R.P. Varma and R. Jindal, Tenside Detergents, 20, 193 (1983).
3. W. Brzyska and W. Hubicki, Ann. Univ. Maide Curie Sklodowksa Soc.,(A/P),  24/25, 69 (1970).
4. A.M. Bhandari, S. Dubey and R.N. Kapoor, J. Am. Oil Chem. Soc., 47, 47 (1990).
5. L.D. Skrylev, V.F. Sazonoma, M.E. Kornelli and N.A. Shukiline, Khim. Khim. I  khnol., 21, 491 (1978).
6. R.C. Mehrotra, Wizz. Z. Friedrich-Schillan Univ. Jena, Math. Naturewise Ket., 14,, 171 (1965).
7. .H. Skellon and K.E. Andrews, J. Appl. Chem. (London), 5, 245 (1955).
8. G. Marwedel, Farbe U. Lack, 60, 530 (1954); 62, 92 (1956).
9. J.H. Skellon and J.W. Spence, J. Appl. Chem. (London), 3, 10 (1953).
10. K.N. Mehrotra, A.S. Gahlaut and M. Sharma, J. Indian Chem. Soc., 65, 397 (1988).
11. J. Indian Chem. Soc., 64, 729 (1987); Acoustics Lett. 12, 107 (1988); Recl. Trav. Pays Bas., 107, 310 (1988); J. Phy. Chem. Liq., 20, 147 (1988).
12.  A. Einstein, Ann. Phys., 19, 289 (1906).
13. V. Vand. J. Phys. Colloid Chem., 52, 277 (1948).
14. G. Jones and M. Dole, J. Am. Chem. Soc., 51, 2950 (1929).

---

This work is licensed under a Creative Commons Attribution 4.0 International License.