Removal of Copper (II) from Aqueous  Solutions using Chalk Powder

Introduction

Copper is a toxic heavy metal discharged into the environment due to various industrial operations¹ and agricultural activities². Anthropogenic sources of copper contamination include smelters, iron foundries, power plant stations and incinerators³. Copper has been found to cause stomach and intestinal distress, kidney damage and anaemia⁴ and prolonged inhalation of copper containing fumes has been linked to increase in lung cancer⁵. US EPA has regulated drinking water concentration not to exceed 1.3 ppm for copper⁶.

The coventional physico-chemical methods for the removal of toxic heavy metals from industrial waste water such as chemical precipitation, electroplating, membrane separation, evaporation or resin ion exchange are usually expensive and sometimes not effective. Therefore, there is a need for some alternative technique which is efficient and cost effective. The search for new technologies involving the removal of toxic metals from waste water has directed attention to biosorption and chemisorption.

In pursuit of low cost adsorbents for the removal of metal ions from aqueous solutions, our attention was drawn towards a readily available and commonly used amorphous solid material — class room chalk. We tried powdered chalk for the removal of arsenic, iron and copper from aqueous solutions for the reason that it has large surface area and microporous character. But we got encouraging results only for copper ions.

In the present work, adsorption of copper (II) from aqueous solutions on powdered chalk was studied as a function of different parameters : contact time (t), mass of the adsorbent (w) and initial concentration (C_i)of the adsorbate. Sorption isotherms were tested for Langmuir and Fruendlich as well as for first and second order kinetic equations.

Material and Methods

The adsorbent, powdered chalk,  was primarily heated in an oven at 105⁰ C for 24 hours and cooled in a desiccator before use in the adsorption process.

Kinetics Batch Adsorption Experiments

Batch adsorption experiments were carried out at ambient temperature. The effects of contact time and mass of the adsorbents were studied by using some common kinetics and equilibrium models. The estimation of Cu (II) ion was carried out spectrophotometrically⁷.   

Effect of agitation time

For the determination of the effect of the agitation time, 1 g of the adsorbent was stirred with a 25 mL solution of copper (II) ions of initial concentration 15 mg/L at specific time intervals. At the end of each time, the solution was filtered rapidly and the copper (II) ion content of the filtrate determined. The difference between the initial (Ci) and the final (equilibrium) (Ce) concentrations was used to calculate the percent removal (% R) of cupric ions using equation (1):

Effect of the amount of adsorbent:

In order to determine the effect of the amount of adsorbent, different masses of the adsorbents (0.5-3g) were treated with 25 ml solution of the copper (II) ion of initial concentration 15 mg/L.

Batch equilibrium experiments 

For each run the adsorbent was mixed with 25 ml solution of cupric ion at different initial concentrations (7-30 mg/L). The suspensions were stirred for 60 minutes by using a magnetic stirrer. The amount of copper ions adsorbed per unit mass of the adsorbent at aquilibrium, q_e (mg/g) was calculated using equation (2):

where, Ci and Ce are copper ion concentrations initially and at equilibrium respectively, V the volume of the solution (mL) and w (gm) the adsorbent mass. The equilibrium data were then fitted by using the Langmuir and the Freundlich adsorption isotherm models.

Langmuir adsorption isotherm

One of the most common isotherm equations for modelling equilibrium data in solid-liquid systems, the Langmuir adsorption equation, is valid for monolayer adsorption onto a surface with a finite number of identical sites which are homogeneously distributed over the adsorbent surface⁸.The general form of the Langmuir equation is :

where, C_e  is the equilibrium concentration of Cu²⁺ ion (g/L), q_e is the amount of  Cu²⁺ ion adsorbed per unit mass of the adsorbent , b is the Langmuir adsorption constant (L/mg) and q_m is the maximum amount of adsorbate per unit mass of adsorbent to form a complete monolayer on the surface (mg/g). The linear form of this equation is as follows :

k_{a =} adsorption rate constant.

k_{b =} desorption rate constant.

Freundlich Adsorption Isotherm

Freundlich equation is an empirical equation based on the adsorption on a heterogeneous surface.

q_e =  k_fC_e ^1/n      ……………………………………….  (5)

where, C_e is the equilibrium concentration of copper ions (g/L) , qe is the amount of copper ions bound per gram of the adsorbent at equilibrium (mg/g) , k_f and n are the Freundlich constants related to sorption capacity and sorption intensity of the sorbent, respectively . The linear form of the Freundlich isotherm equation is:

log q_e =  log k_f  + log C_e       ……………………………..  (6)                           

[ n= 1/n_f  : where , n_f =Adsorption affinity (dimentionless)]

Kinetic adsorption experiments

Kinetic adsorption experiments were conducted using a series of 25 mL solutions containing fixed amounts of adsorbent and cupric ions. The solutions were vigorously agitated with a magnetic stirrer for increasing time intervals. At the end of each run, the solution was filtered and the Cu²⁺ ion concentration in the filtrate was determined. This study has been carried out for two different Cu²⁺ concentration. Following kinetics models have been used to fit experimental data.

The pseudo-first order model

The pseudo-first order equation of Lagergran is generally expressed as follows⁹:

where, q_e and q_t are the sorption capacities at equilibrium and at time, t  respectively (mg.g^-1) and k₁ is the rate constant of pseudo-first order sorption (L.min^-1). Equation (7), after integration and applying boundary conditions, t = 0 to t = t and q_t = 0 to qt = qt, becomes :

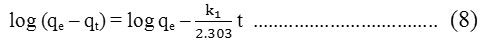
The pseudo-second order model :

The pseudo-second order chemisorption kinetic rate equation is expressed as ¹⁰ :

where, k₂ is the rate constant of pseudo-second order sorption (g.mg^-1.min^-1).

The integrated and rearranged form of equation (9) is :

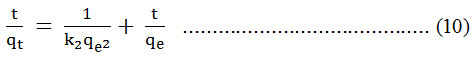
Results and Discussion

Effect of agitation time

The plot of % removal of cupric ions against varying contact times are shown in figure 1. Cu²⁺ ion uptake increases with increasing agitation time within 60 minutes and then it becomes nearly constant.

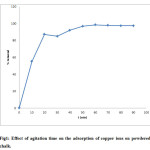Figure 1: Effect of agitation time on the adsorption of copper ions on powdered chalk.  Click here to View figure

 

Effect of the amount of adsorbent 

For this experiment, different masses of adsorbents were stirred with cupric ion solution for 60 minutes. The results are depicted in figure 2. Copper (II) ion adsorption percentage increases with adsorbent mass (m) significantly upto 1 g and then becomes constant. Increase in adsorption percentage is due to the increase in available number of binding sites when the amount of adsorbent mass increases¹¹. Maximum adsorption percentage is 98.2% using powdered chalk at 1g sample weight.

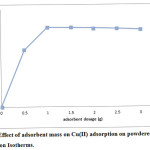Figure 2: Effect of adsorbent mass on Cu(II) adsorption on powdered chalk. Click here to View figure

 

Adsorption Isotherms.

Equilibrium studies were conducted with 1g of powdered chalk. These results are shown in figure 3.

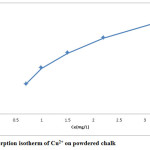Figure 3: Adsorption isotherm of Cu2+ on powdered chalk. Click here to View figure

 

Adsorption isotherm on powdered chalk is type I adsorption isotherm, characteristic of microporous adsorbent, chemical adsorption or physical adsorption limited to monolayer coverage.

Data obtained from these studies have been tested with the Langmuir and Freundlich linearized equations. These results are summarized in table 1. As these results show, adsorption isotherm is in agreement with the Langmuir adsorption isotherm. The higher is the b value, the stronger is the adsorbate-adsorbent interaction.

Table 1: Isotherm parameters for Cu²⁺ uptake from aqueous solutions.

Adsorbent	Langmuir Parameters			Freundlich Parameters
	b	qm (mg/g)	r2	kf	1/n	r2
Powdered Chalk	0.06	53.2	0.9724	0.33	0.88	0.9663

Kinetic modelling of Cu²⁺ ion adsorption 

The kinetics of the adsorption of cupric ions has been studied using two kinetics models. In order to obtain parameters related to each kinetic model, experimental data have been tested with linear forms of these models. The straight-line plots are presented in figures 4 & 5. Parameters are given in table 2.

Table 2: Kinetic model parameters for Cu²⁺ adsorption on powdered chalk.

Adsorbent		Powdered Chalk
Ci (mg.L-1)		17	28.5
Pseudo-first order	k1/10-2 min-1	8.978	4.9
	qe (mg/g)	3.9	6.1
	r2	0.9949	0.9954
Pseudo-second order	k1/g.mg-1.min-1	7.843 x 10-3	1.083 x 10-3
	qe(mg/g)	–	–
	r2	0.9923	0.7614

As evident from above results the adsorption of cupric ion on powdered chalk can be well described by the pseudo-first order kinetic model, with a correlation coefficient greater than 0.9900. The value of the rate constant decreases when initial Cu²⁺ ion concentration increases, suggesting that the adsorption mechanism of cupric ions on powdered chalk is the rate-limiting step¹².

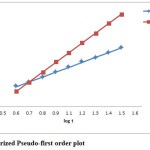Figure 4 : Linearized Pseudo-first order plot. Click here to View figure

 

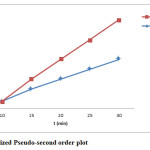Figure 5: Linearized Pseudo-second order plot. Click here to View figure

 

Conclusion

The present investigation reveals that powdered chalk is an efficient material for the remediation of copper (II) ion contamination. Maximum removal percentage of 98.2% can be achieved. Adsorption capacity is also quite high (qm =53.2 mg/g). Adsorbate-adsorbent interactions are also strong. Adsorption kinetics is pseudo- first order.

Acknowledgement

The authors are grateful to the University Grants Commission, New Delhi for providing financial assistance under Major Research Project Scheme.

References

1. Klimmek S., Stan H. J., Wilke A., Bunke G. & Buchholz R., Environ. Sci. Technol., 35: 4283-4288 (2001).
2.  Hawari A. H. & Mulligan C. N., Bioresour Technol., 97: 692–700 (2006).
3. Vilar V.J.P., Botelho C.M.S. & Boaventura A.A.R., Bioresour Technol., 99: 750-762 (2008).
4. Yu B., Zhang Y.,Shukla A., Shukla S. S. & Dorris K. L., J. Hazard Mater., B 80: 33-42 (2000).
5. Carson B. L., Ellis V. & McCann J. L., Toxicology and Biological Monitoring of Metals in Humans, 71, Lewis Publishers, Chelsa, Michigan, 133 (1986).
6. Wang J., Process Biochem., 37: 847-850 (2002).
7. APHA, Standard Methods of Examination of Water and Wastewater, 19th edition, American Public Health Association, Washington DC (1996).
8. Langmuir I., J. Am. Chem. Soc., 40: 1361-1368 (1916).
9. Lagergran S. & Kungliga S., Handlingar Band., 24(4): 1 (1898).
10. Ho Y. S. & Mckay E., Can J. Chem. Eng., 76: 822-827 (1998).
11. Krishnan K. A. & Anirudhan T.S., J. Hazard. Mater., 92: 161-183 (2002).
12.  Kushwaha Shilpi & Sodaye Srparna P., PETWAS., 33: 617 – 623 (2008).

---

This work is licensed under a Creative Commons Attribution 4.0 International License.