Influence of Hydration on the Neutral Complex (-OH, H₃O+) (H₂O)n

Introduction

The state of a proton in aqueous solution and clusters is of wide interest and the proton Transfer reaction is one of the most important in chemistry [1]. Proton transfer also plays a very important role in biological processes [2-5], however a proper description of such a process is still a major challenge for theoretical chemistry. Advances in theory and the availability of increased computer power have allowed substantial progress to be made for proton transfers in solution [6-8] and clusters [9,10].

In recent months, the methods and techniques of density functional theory(DFT) have advanced remarkably[11].They show considerable advantages of generality and accuracy with respect to the semiempirical  methods and are more rapid than the highly correlated traditional ab initio methods that are required to treat questions of reactivity. They have been used to study small hydrated proton clusters H₂O⁺⁵ [12,13]  and other hydrogen-bonded systems [14]. The energy barrier to proton transfer was calculated using [12] and compared with the results of other computational methods. A combined ab initio density functional and classical molecular dynamics simulation (DFT CDFMD) [15] is under development to study quantum molecules in solution. It can be applied, in its present state, to calculate the free energy barriers of proton transfer in solution.

Small clusters provide a unique solvent environment, where reaction dynamics can be very different from that in aqueous solution. Recent advances in laser technology and molecular beam spectroscopy allow experimentalists to provide detailed information on the structure of the cluster. High resolution vibration-rotation spectroscopy of the hydrated hydronium ions, e.g., H₅O⁺², H₇O⁺³ and H₉O⁺⁴ have been obtained by lee’s group [16]  .Many ab initio calculations have been published for H₅O⁺² [9,10,12]. However, to our knowledge, except for some earlier results of Newton [17] and unpublished works of Remington and Schaefer [18], very few ab initio results are available for the optimised structures and vibrational analyses for larger hydrated proton clusters.

 In this paper, we report the ground state structures and the vibrational analysis for the hydrated proton the neutral complex (^–OH, H₃O⁺)(H₂O)_n.lusters with n=0,1and 3. Few of the method used in ab initio are designed to probe the solvent effects on the energy barriers of proton transfer in the hydrated proton the neutral complex.

The aim of our research is to study the effect of the interaction of several bodies on the structure of complex systems in the neutral (^–OH, H₃O⁺)(H₂O)_n, with (n = 0, 1, 3). These systems represent great interest in a chemical point of view in the biological field.

The study of these systems, it also provides information on the structure, the number of coordinate hydration and the nature of the routesto from neutral complexes.

Our job is to study the properties of aqueous ionic solutions by ab initio calculations on the systems:(^–OH, H₃O⁺) with symmetry C₁, (^–OH, H₃O⁺)(H₂O) with symmetry C₁, (^–OH, H₃O⁺)(H₂O)₃, with symmetry C_s. We will discuss three methods: Hatree-Fok, Moller Plesset perturbation, DFT with the 6-31 + G basis.

The remainder of this article is divided into three parts. The computational method is discussed in Sec.II, results are presented in Sec.III, and our conclusions are briefly summarized in Sec.IV.

II.Computational Methods

We have computed the optimal geometries and harmonic vibrational frequencies of complex systems in the neutral (^–OH, H₃O⁺)(H₂O)_n, with (n = 0, 1, 3).A geometry was considered as optimised when the gradient was less than 0.0001 a.u.

All calculations were carried out in the ab initio [19] molecular orbital ( MO) framework, using basis sets of contracted Gaussian-type orbitals (GTO’s). The intergral and SCF programs employed are those recently developed by Hehre and Pople [20] .Wedesired a basis set sufficiently flexible to give reasonable quantitative account of the structure and intermolecular energitics of the system under study while at the same time small enough so that a detailed study of potential energy surfaces of interest might be carried out economically. In preliminary minimal-basis calculations 6-31 + G ** [27] This includes polarization functions on all atoms

with different levels; coerenti self-field Hartree-Fock  (HF) [21], the perturbation method of Moller-Plesset (MP) to second order [28-29]., the density functional method (DFT) [22-26] calculations with the perdew nonlocal corrections to exchange and correlation give somewhat shorter hydrogen bond lengths.

III.Results And Discussion

We studied the influence of hydration of the neutral complex (^–OH, H₃O⁺)(H₂O)_n, by ab nitio’s calculation  ,with  structural,  vibrational ,and energitical point of view. We started our study with the complex (^–OH, H₃O⁺) which has a symmetry with the C₁ complex then (^–OH, H₃O⁺)(H₂O) with a C₁ symmetry and the complex(^–OH, H₃O⁺)(H₂O)₃ which has a C_s symmetry, this study has been addressed by methods HF, MP2 and DFT / B3LYP with the 6-31 + G **, all results are grouped in Tables (1,2,3,4).

The intra-and intrermolecular coordinates complex (^–OH, H₃O⁺) were optimized by three methods is (Table.1) . The system stabilizes at a level of energy – 95426.04 kcal / mol by the HF method, we notes in (Fig.1). The donor monomer ion H₃O⁺ has three covalent bonds, two bonds among them in the same plans, those formed by the oxygen atom O₁ and the hydrogen atoms H₄, H₂ which has a distance O₁-H₄ and O₁-H₂ equivalent to 0.944 Å. The route that is outside of the plan is formed by the O₁ oxygen atom and the hydrogen atom H₃ at a distance O₁-H₃ of 0.963 Å. The angle O₁-H₃-H₄ is 117.1 °, the angle of H₃-O₁-H₂ is 114.8 °. °H₂-H₄-O₁ is 107.1 °, these three angles are closed to the angle 120°.

 

The donor monomer combined with the acceptor monomer^–OH by  a O₅…H₄   hydrogen at a distance of 2.001 Å , which confirms that the three atoms O₁, O₅ and H₄ are  in the same plane almost linear. A comparison of results with the values found in experimental observation hat the HF method is close to the experimental 0.04008% compared to the DFT method 0.04358%  and the MP2 method 0.04226%.

The vibrational study of complexes with different methods HF, MP2 and DFT was made by the 6-31 + G ** basis, see (Table.2).

This table has been divided into two parts the first is the intermolecular vibration and the second intermolecular vibration. To explain this bungs have chosen the  HF method,  the appearance of three frequency bungs (137-630, 1743-1758, 4096-4257)Cm^-1 of varying intensities (Table.2). The two first  bungs correspond to intermolecular vibrations and the third bung corresponds to the intermolecular vibrations, the frequency bung (4096-4257) Cm^–, reply the OH stretch vibration, the band (1743-1758) Cm^-1 is consistent with the deformation vibration (Bending), and the bung (137-630) Cm^-1 corresponds to the intermolecular vibrations of the OH bridge linking hydrogen
].  O-H….. O]. A comparison with experimental values 3385 and 3490 Cm^-1 reflects the values of frequencies calculated (Table2).

The next step, we add to this complex a water molecule to see the influence of the latter on the neutral complex (^–OH, H₃O⁺). The system (^–OH, H₃O⁺)(H₂O) stabilizes with C₁ symmetry, see (Fig. 2) at an energy level -143147.7 k cal / mol for the HF method see (Table 3). A comparison of results found with the experimental observation that in the HF method is closed to the experimental 0.04008 % compared to the DFT method 0.04358 % and the MP2 method 0.04226 %[30]. We noticed that there’s a decrease of O-O distance of about 0.12 Å, and  hydrogen bond distance of about 0.19 Å, there also a significant increase in binding of the ^–,OH ion H₃O ⁺ with a value of approximately 0.035 Å, and an increase in the angle of the ion of about 6 °even (Table 3).

 

The calculation of frequencies of vibration in these complexes restores the bung in the same frequency range, but with different intensities (Table.4) and the bung (277-870) Cm^-1 corresponds to the intermolecular vibrations of the OH bridge linking hydrogen. O-H …..O., three  (648,401, 617, 83, 583, 861) Cm^-1  reply to  the three hydrogen bonds of the appeared complex. By comparison with experimental values 3385 and 3490 Cm^-1 . We deduct, that the experimental values correlate well with the frequency values calculated for different levels in (Table.4). We recently added to the neutral complex (^–OH, H₃O⁺) three water molecule to study the intra-and intermolecular interaction of the system(^–OH, H₃O⁺)(H₂O)₃ , with an even symmetry C_s (Fig .3), an energy level – 95933.46 k cal / mol for the HF method see (Table 3).The results are shown in Table 3 and Tables .4., A comparison with results found in the experimental observation ,also we notice that the DFT method is closed to the experimental 0. 0152 % compared to the HF method 0. 0215 % and the MP2 method of 0. 0243 % . By varying the coordinat number there was a slight increase in distance R O-O 0. 02 Å with a slight increase in hydrogen bonding distance of 0. 21 Å. There is a decrease of O-H bond in relation to the first with a value of 0. 01 Å, with a decrease of angle to the first with a value of 2 °. even .1,2,3 figures.

The calculation of frequencies of vibration in these complexes, gives a band (181-840)

Cm^-1corresponds to the intermolecular vibrations of the O-H bridge linking hydrogen
O-H …..O six frequencies (534.352- 566.166- 608.95- 696.731-811.627-833.038) Cm^-1  responds to the six hydrogen bonds of appeared complex. and other bungs frequencies in the same interval but with different intensities (Tableau.4) that can be explained by the number of coordinat hydration and their positions (the symmetry of the complex),  simply the influence of hydration has a great interest on the structure of the complex (^–OH, H₃O⁺) in  comparison with experimental values 2700 Cm^-1 , 3025 Cm^-1 , 2600 Cm^-1 [33] and 2800 Cm^-1, it is deduced that the experimental values correlate well with the values calculated for different frequency levels.

IV. Conclusion
A comparative structural and intra-and intermolecular energy by different levels MP2, HF, DFT with 6-31 + G ** basis on the neutral system (^–OH, H₃O⁺)(H₂O)_n. The analysis of results has allowed us: to determine the configurations of coordinates that represent the complex neutral (^–OH, H₃O⁺)(H₂O)_n. We notice that there is an important bonding increase of the ^–OH, H₃O⁺ by adding water molecule in the complexe. In the comparative study of the hydrogen bond distance of a monomer to monomer donor acceptor complex in the neutral, we find that the distance O….H was reduced by the addition of three water molecules in complex and the energy gets weaker more and more by the addition of water molecule to the complex, it is predicted by the frequency of vibration.
We can conclude that this study has provided information on the structure, number of coordinat hydration and nature of the neutral complexes bonds, and our results give an excellent agreement with experimental values.

Table 1: The geometric parameters calculated at different levels of (^–OH, H₃O⁺)   and the comparison between results from experimental values.

Internal Coordinate	HF	MP2	DFT	Experiment a
R(O(1) -H(4)), [Å] R(O(1) -H(2)), [Å] R(O(1) -H(3)), [Å] y(H(3)-O(1)-H(2)),°. y(H(1)-O(4)-H(5)),°. y(H(3)-O(1)-H(4),°. y(H(2)-O(1)-H(4)),°. R(O(5) -H(6)), [Å] R(O(5) -H(4)), [Å]	0. 94417 0. 94423 0.96353 114. 8552 55.9870 117. 13855 107. 13855 0. 94244 2. 001234	0. 9643 0. 9643 0, 97561 116. 0936 55. 2015 115. 2018 105. 679 0. 9624 2. 009184	0. 9658 0. 9658 0. 965859 113. 1782 53. 5312 112. 3741 106. 0589 0. 9642 1. 923828	0. 950 0. 950 0. 950 111. 2 – 111. 2 104.5 0. 950 –

^aReference 30

Table 2 : Harmonic vibration frequencies (in Cm ^-1) in the complex (^–OH, H₃O⁺) and experimental values the comparison between  results from previous and experimental values.

	System	MP2 (cm -1 )	MP2 IR Intensities (km/mol)	HF (cm -1 )	HF IR Intensities (km/mol)	DFT (cm -1 )	DFT IR Intensities (km/mol)	Expriment a (cm -1 )
Intermolecular
ω9(a”)	Acceptor asymmetric O-H Stretch	4000. 68	95. 8597	4257. 29	121. 565	3924. 24	86. 8857
ω1(a’)	Donor free O-H Stretch	3978. 55	124. 758	4244. 24	146. 707	3898. 78	95. 0156	3490
ω2(a’)	Acceptor symmetric O-H Stretch	3861. 32	14. 244	4141. 42	29.0664	3808. 5	13. 9001	3385
ω3(a’)	Donor bridge H Stretch	3788. 01	260. 284	4096. 08	213. 66	3696. 96	332. 356
ω4(a’)	H3O+ donor bend	1658.37	64.9643	1758. 94	92.7181	1631. 95	46.8163
ω5(a’)	–OH acceptor bend	1636.92	109. 655	1743. 95	135. 431	1616. 03	123. 793
ω10(a”)	H..(H-O-H) Out of plane donor bend	676.401	192. 918	630.804	232. 658	681.336	171. 814
ω6(a’)	In- plane donor wag	372. 019	128. 61	359. 79	140. 984	393. 602	97.2357
ω7(a’)	O-O stretch	202. 215	172. 523	186. 384	248. 51	205. 659	198. 959
ω8(a’)	Acceptor bend	178. 67	67.7546	167. 948	78. 2911	179. 521	35. 652
ω11(a”)	Acceptor twist	170. 78	129. 816	157. 579	87 . 4746	170. 518	128. 775
ω12(a”)	Donor torsion	144. 827	143. 051	137. 783	136. 708	144. 128	182. 66

 

Table 3: internal study structure of the coordinate by taking into account the inter and intra-molecular interactions on the studied complexes .

		HF			MP2			DFT		Experiment
	n= 0	n=1	n=3	n= 0	n=1	n=3	n= 0	n=1	n=1
Intermolecular
R(O-O) [Å]	2. 83405	2. 8872	2. 90 392	2. 91435	2.79677	2. 80547	2. 889690	2. 78975	2.785082	–
R(O…H-O) [Å]	2. 00123	2. 0341	2. 04913	2. 00918	1. 9194	2. 03678	1. 923828	1. 8834	2. 040007	–
a y(H-O…H)	55. 9870	148. 3984	107. 637	55. 2015	147. 363	107. 574	53. 5312	149. 38	107. 9534	104.5 a
b y(H-O-H) °	117. 1385	91. 679	98. 815	115. 201	91. 6705	92. 3665	112. 3741	90. 951	97.15347	104.5 a
	107. 1385	107. 588	107. 869	105. 679	106. 476	106.714	106. 0589	106. 914	106. 951	111.2 a
	114. 8552	129. 6005	132. 895	116.  093	127. 810	131. 338	113. 1782	124. 22	130. 548	–
R(O-H)c   [Å]	0..94417	0. 9508	0. 959813	0. 9643	0. 97561	0. 98345	0. 9658	0. 9801	0.985645	0. 950 a
	0. 94423	0. 9427	0. 960	0. 9643	0. 97561	0. 963	0. 9658	0. 9643	0. 972	1. 017± 0.005b
	0. 96353	0. 9589	0. 97123	0. 97561	0. 9612	0. 9749	0. 96586	0. 983	0. 984084	1. 01± 0.01c
R(O-H)d   [Å]	0. 94244	0. 9424	0. 96201	0. 9624	0. 9627	0. 9758	0. 9642	0. 964	0. 964	0. 964 a

^a Angle antre les deux  ions ^y(O-H…O)

^b Angle de lion H₃O⁺

^c Distance de lion H₃O⁺

^d Distance de lion OH^–

^aReference 30

^bReference 31

^cReference 32

 

Table 4: Harmonic vibration frequencies (in Cm ^-1) in the complex undermentioned and comparison between the experimental values.

System	MP2 (cm -1 )	MP2 IR Intensities (km/mol)	HF (cm -1 )	HF IR Intensities (km/mol)	DFT (cm -1 )	DFT IR Intensities (km/mol)	Expriment (cm -1 )
(–OH, H3O+)( H2O)	3969, 37	121, 161	4426, 65	946, 269	3899.19	57.2785	3490
	3967, 98	111, 378	3980, 03	140, 362	3898.01	106.036	3385
	3964, 63	110, 833	3945, 8	27, 3588	3893.22	97.4185
	3730, 38	405, 507	3942, 27	93, 1109	3616.28	541.255
	3722, 19	444, 006	3677, 15	633, 836	3603.68	596.1
	1653, 42	116, 771	1828, 27	196, 862	1631.08	111.833
	1649, 01	132, 572	1757, 69	74, 0879	1626.48	117.6
	861.006	19.3183	915, 145	317, 613	912.853	16.1281
	700, 657	455, 086	834, 851	319, 188	722.42	428.2
	565, 813	179, 755	719, 518	53, 503	604.778	213.997
	347, 639	124, 807	648.401	147.529	473.567	153.197
	259, 698	42, 5834	617, 83	126, 958	380,.945	50.2188
	210, 193	180, 261	583, 861	199, 244	270, 584	32, 195
	192, 581	12, 1642	371, 754	55, 4202	250, 727	64, 5898
	451, 07	150, 232	276, 676	8, 2816	177, 446	120, 171
(–OH, H3O+)(H2O)3	3775,99	693,479	423994	191,149	3896.98	60.5471	3025
	3722,56	143,642	4237,5	189,00	3895.4	130.992	2800
	3712,24	627,636	4127,91	517,08	3894.05	126.164	2700a
	3708,41	184,877	4063,3	453,999	3644.82	832.215	2600a
	3667,24	287,406	4036,96	199,898	3597.31	535.396
	1651,57	143,642	1790,09	22,4773	3592.66	965.33
	1648,81	115,974	1751,9	174,096	1431,06	186,177
	897.157	29.0476	833.038	106.803	779.342	439.353
	760.545	412.5	811.627	4.2433	690.921	32.6021
	668.238	417.687	696.731	512.902	670.105	288.214
	641.291	24.0444	608.95	461.502	633..506	155.281
	598.752	267.709	566.166	19.4118	572.159	161.968
	404,899	115.238	534.352	263.968	430.787	25,2856
	380,691	162,138	473,519	142,43	416,043	145,337
	213,472	122,684	366,969	137,189	386,379	386.622
	226,801	165,693	205,617	70,304	270, 584	13,8428
	193,942	144,634	237,448	11,1279	250, 727	32, 195
			180,813	67,7975	198,492	21,3725

^aReference 33.

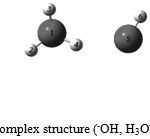Figure 1: The neutral complex structure (–OH, H3O+) with C1 symmetry.: Click here to View figure

 

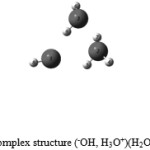Figure 2: The neutral complex structure (–OH, H3O+)(H2O) with C1 symmetry.: Click here to View figure

 

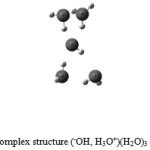Figure 3: The neutral complex structure (–OH, H3O+)(H2O)3 with CS symmetry.: Click here to View figure

 

References

1. G.W.Robinson, P.J.Thistlethwaite, and J.Lee,J.Phys.Chem.90.4224(1986).
2. E.N.Baker and R.E.Hubbard, Prog.Biophys.Mol.Biol, 44,97(1984).
3. G.A.Jeffrey and W.Saengeri, in Hydrogen Bonding in Biological Structures (Springer, New York,.1991).
4. Y.Cha,C.J.Murray, and J.P.Klinman, Science 243, 1325 (1989);J.Rucker, Y.Cha, T.JONSSON, K.L.Grant, and J.P.Klinman, Biochemistry 31, 11489 (1992).
5. A.Warshel,Computer Modelling of Chemical Reactions in Enzymes and Solutions (Wiley, New York, (1991)
6. D.Borgis, S .Lee, and J.T.Hynes, Chem.Phys. Lett.19,162 (1989); D.Borgis, G.Tarjus, and H.Azzouz, J.Phys. Chem;96,3188 (1992); D.Li and G.Voth, ibid, 95,10425 (1991).
7. D.Borgis and J.T.Hynes, J.Chem.Phys. 94, 3619 (1991).
8. D.Laria, G.Ciccotti, M.Ferrario, and R. Kapral, J.chem. Phys. 97, 378 (1992);J.Lobaugh and G.A.Voth, Chem.Phys. Lett. 198, 311 (1992).
9. S.Scheiner, Acc.Chem.Res.18, 174 (1985).
10. K.Luth and S.Scheiner, J.Chem.Phys.97, 7507 (1992); Z.Latajka and S.Scheiner, J.Mol.Struct. 234, 373 (1991).
11. D.R.Salahub, M.A.Castro, and A.Proynov, in Relativistic and Electron Correlation Effects in Molecules and Solids, edited by G.L.Malli (Plenum, New York, 1994).
12. C.Mijoule, Z.Latajka, and D.Borgis, Chem.phys.Lett. 208, 364 (1993).
13. Santhanamoorthi Nachimuthu, Jiali Gao, Donald G. Truhlar Chemical Physics 400 (2012) 8–12
14. F.Sim, A St-Amant, I.Papai, and D.R.Salahub, J.Am.Chem.Soc 114, 4391 (1992).
15. D.Q.Wei and D.R.Salahub, Chem. Phys.Lett. 224, 291 (1994).
16. L.I.Yeh, M.Okumura, J.D.Myers,J.M.Price, and Y.T.Lee, J.Chem.Phys 91, 7319 (1989).
17. M.D.Newton, J.Chem.Phys.67, 5535 (1977).
18. R.Remington and H.F.Schaefer (unpublished results) quoted in Ref.15.
19. David. Tozer, Chengteh Lee and George Fitzgerald, J.Chem.Phys.104, 5555 (1996).
20. Selinger and A.W.Castleman. Jr,  J.Phys.Chem.95,8442(1991).
21. C.Moller and M.S.Plesset, Phys.Rev.46,618 (1934).
22. W.Kohn and L.J.Sham, Phys. Rev.A.140,A1133 (1965).
23. Density Functional Methods in Chemistry, edited by J.K.Labanowski and J.W.Andzelm (Springer-Verlag, New York, (1991).
24. F.Sim.A. St. Amant.J.Papai, and D.R.Salahub, J.Am.Chem.Soc.114,4391 (1992).
25. H.B.Schlegel,J.Comput,Chem.3,214(1982).
26. Gaussian98. Revision.M.J.Frisch,G.W.Trucks,II.B.Schlegel.G.E.Scusecria,M.A.Robb, J.R.Cheeseman,V.G.Zakrzewski,J.A. Montgomery, Jr.r.e.Stratmann, J.C.Burant, S.Dapprich, J.Millam,A.D.Daniels, K.N.Kudin, M.C.Strain, O.Farkas, J.Tomasi,V.Barone,M.Cossi,R.Cammi, B.Mennucci, C.Pomelli, C.Adamo, S.Clifford, J.Ochterski, G.A.Pertersson, P.Y.Ayala, Q.Cui, K.Morokuma,D.K.Malick,A.D.Raduck,K.Raghavachari,J.B.Forestman,J.Croslowski,J.V.Ortiz,B.B.B.Stetanov,G.Liu,A.Liashenko,P.Piskorz,I.Komaromi,R.Gomperts,R.L.Martin,D.J.Fox,T.Keith,M.A.AI-Laham, C.Y.Peng,A.Nanayakarra,C.Gonzalez, M.Challacombe,P.M.W.Gill, B.Johnson,W.Chen,M .W.Wong,J.L.Andres,L.Gonzalez,M.Head-Gordon,F.S.Replogle and J.Apople,Gaussian,Inc ,Pittsburgh PA ,(1198).
27. J.A.Pople, R.Seeger, and R.Krishnan, Int.J.Quantum Chem.Symp.11149 (1977)14.
28. R.Krishnan and J.A.Pople, Int.J.Quantum. Chem.14, 91 (1978).
29. R.Krishnan, M.J.Frisch, and J.A.Pople, J.Chem.Phys.72,4244(1980).
30. K.Kuchitsu and Y.Morino, Bull.Chem.Soc. Japan. 38, 814 (1965).
31. J.O.Lundgren and I.Olovsson, J.Chem.Phys.49, 1068(1968).
32. J.O.Lundgren and J.M.Williams, J.Chem.Phys.58, 788 (1973).
33. P.A.Giguére and S.Turrell, Can.J.Chem.54, 3477(1976).,Inspec,  this work is a followup of an earlier, pioneering study by M.Falk and P.A.Giguére, Can.J.Chem.35, 1195(1957).

---

This work is licensed under a Creative Commons Attribution 4.0 International License.