Ft-Ir, Ft-Raman and Computational Study of Phenylurea

Introduction

Thiourea and substituted thioureas are versatile precursor units in the synthesis of many useful heterocyclic compounds¹ .Theoretical study of the Hg2+ recognition by 1,3- diphenylthiourea has been reported². More recently, interest has been shown in the substituted phenylurea compounds in terms of their activity on grapes and tree fruits³. Certain Phenylurea herbicide is used for the control of broadleaf weeds in cereal and vegetable crops, acting through the inhibition of photosynthesis⁴ .Phenyl urea is used in washing and leaching processes, but degrades slowly⁵ .The mechanism of enantioselective Michael addition of acetylacetone to a nitroolefin catalyzed by a thiourea based chiral bifunctional organocatalyst is investigated using density functional theory calculations⁶ .Yang et al.⁷ reported the structural and spectroscopic study of N-2-fluorobenzoyl-N‘-4-methoxyphenyl thiourea. Badawi reported the structural stability, C-N internal rotations and vibrational spectral analysis of non-planar phenylurea and phenylthiourea⁸. Metal organic coordination compounds as non linear optical materials have attracted much more attention for their high NLO coefficients, stable physico-chemical properties and better mechanical intension. Many metal organic coordination complexes of thiourea materials with good NLO effects have been designed and synthesized^9-14. Pfeffer et al.¹⁵ reported the anion recognition using pre-orgranized thiourea functionalized polynorbornance receptors. There is currently great interest in the development of supramolecular systems that have the ability to bind and signal the presence of anions, as well as transporting such species across vesicle and cell membranes^{16, 17}. Molecules that possess functional groups such as amides, ureas and thioureas^18-20 have proven to be particularly effective in this regard as they are able to bind anions using directional hydrogen bonding interactions. Thiourea and substituted thioureas are especially important for their nonlinear optical properties. In the present study the FT-IR, FT-Raman and theoretical calculations of the wavenumbers of the title compound are reported.

Experimental

The FT-IR spectrum was recorded using a DR/Jasco FT-IR 6300 spectrometer. The spectral resolution was 2 cm^-1.  The FT-Raman spectrum was obtained on a Bruker RFS 100/s, Germany. For excitation of the spectrum the emission of Nd:YAG laser was used, excitation wavelength 1064 nm, maximal power 150 mW.

Computational Details

Calculations of the title compound were carried out with Gaussian09 software program²¹ using the HF/6-31G* and B3LYP/6-31G* basis sets to predict the molecular structure and vibrational wavenumbers. The DFT hybrid B3LYP functional method tends to overestimate the fundamental modes; therefore scaling factors have to be used for obtaining a considerably better agreement with experimental data^22. The wavenumber values computed contain known systematic errors and we therefore, have used the scaling factor values of 0.8929 and 0.9613 for HF and DFT basis sets²². The assignment of the calculated wavenumbers is aided by the animation option of Gaussview program, which gives a visual presentation of the vibrational modes^23.

Results and Discussion

IR and Raman spectra

The observed IR, Raman and calculated (scaled) wavenumbers and assignments are given in Table 1. The carbonyl group is contained in a large number of different classes of compounds, for which a strong absorption band due to the C=O stretching vibration is observed in the region²⁴ 1750–1600 cm⁻¹.  If a carbonyl group is part of a conjugated system, then the wavenumber of the carbonyl stretching vibration decreases, the reason being that the double-bond character of the C=O group is less due to the π-electron conjugation being localized. For the title compound, the υC=O mode is seen as a strong band at 1655 cm⁻¹ in the IR and at 1658 cm⁻¹ in the Raman spectrum. The DFT calculations give the corresponding mode at 1667 cm⁻¹. The deformation bands of the C=O group are also identified (Table 1).

The NH stretching vibration²⁶ appears as a strong broad band in the region 3390 ± 60 cm⁻¹. In the present study, the NH stretching band is observed at 3439 cm⁻¹ in the IR spectrum. The corresponding calculated values (DFT) are 3475 cm⁻¹. El‐Asmy and Al‐Hazmi²⁸ reported υNH in the region 3138‐3323 cm⁻¹. The CNH vibrations in which N and H atoms move in opposite directions of the carbon atom in the amide moiety appear at 1530 cm⁻¹ in the IR spectrum and at 1526 cm⁻¹ theoretically (DFT) and the CNH vibrations in which N and H atoms move in the same direction of the carbon atom in the amide group appear at 1328 (IR) and 1333 cm⁻¹ (DFT)^29-31 .The NH rock in the plane is observed at 1166 cm⁻¹ in the IR spectrum, 1170 cm⁻¹ in Raman spectrum and the DFT calculations give this mode at 1175 cm^{−1 31} .The out‐of‐plane wagging²⁶ of NH is moderately active with a broad band in the region 790 ± 70 cm⁻¹ and the band at 829 cm⁻¹ in the Raman spectrum and 829 cm⁻¹ (DFT) are assigned as this mode. El‐Shahawy et al.³¹ reported a value 710 cm⁻¹ for this mode. Badawi reported⁸ the NH vibrational modes at 3315, 1498, 1268 cm⁻¹ in the IR spectrum, 3320, 1508, 1264 cm⁻¹ in the Raman spectrum and at 3617, 1502, 1256 cm⁻¹ theoretically. Panicker et al.³² reported the NH bending modes at 1538, 1220 cm⁻¹ in the IR spectrum and at 1558, 1223 cm⁻¹ theoretically (DFT).The C‐N stretching vibration²⁶ coupled with δNH, is moderately to strongly active in the region 1275 ± 55 cm⁻¹. El‐Shahawy et al.³¹ observed a band at 1320 cm⁻¹ in the IR spectrum as the υCN mode. Yang et al.⁷ reported aromatic CN stretching band at 1359 cm⁻¹. In the present case, the bands at 1255 cm⁻¹ in the IR spectrum and at 1290, 1256 cm⁻¹ in the Raman spectrum are assigned as this mode. The DFT calculations give the corresponding bands at 1286, 1251 and 995 cm⁻¹.

The NH₂ scissoring vibrations of aromatic amines, expected²⁶ around 1650 cm⁻¹ appear at around 1616 cm⁻¹ in the IR spectrum and at 1618 cm⁻¹ from the calculation. The δNH₂ scissoring vibrations are reported at 1629 cm⁻¹ for sulfanilamide³³ and at 1637 cm⁻¹ in IR, 1634 cm⁻¹ in Raman and 1642 cm⁻¹ in HF for orthanilic acid³⁴. The δNH2 scissoring modes are reported at 1621, 1597 cm⁻¹ (IR),1621, 1602 cm⁻¹ (Raman) for para substituted halogeno anilines³⁵ and at 1630 cm⁻¹ for 2-aminobenzyl alcohol^36. According to Roeges²⁶ ρ/τNH₂ vibration is expected in the region 1070 ± 50 cm⁻¹ and in the present case the band observed at 1060 cm⁻¹ (IR) is assigned as ρ/τNH₂ modes. The DFT calculations predict these modes at 1052 cm⁻¹.  For orthanilic acid³⁴ these modes are reported at around 1101 cm⁻¹ experimentally and at 1112 cm⁻¹ theoretically. Krishnakumar and Balachandran³⁷ and Altunet al^.38 reported these modes at 1130,1126, 1089, 1085 cm⁻¹ for dibromo, nitro and methylthioaniline complexes, and at 1040, 1030, 1008 cm⁻¹ for methyl aniline complexes, respectively. Kurt et al ³⁹ for chloromethylaniline at 667 cm⁻¹ in IR spectrum and at 695 cm⁻¹ in HF calculation. Tzeng et al ⁴⁰ observed the ωNH₂ vibration calculated the wavenumber of wagging vibration of aminogroup at 649 cm⁻¹ and experimentally at 665 cm⁻¹ and established the mixing between the out-of-plane amino group wagging and the δPh bending of aniline^{39, 40}. For the title compound, the wagging vibration of NH₂ is assigned at 533 cm⁻¹ theoretically, which is consistent with its expected presence in the region²⁶ of 620 ± 100 cm⁻¹.

Phenyl CH stretching modes²⁶ are expected above 3000 cm^-1 and  for the title compound, the bands observed at 3072 cm^-1 in the Raman spectrum and at 3035 cm^-1 in the IR spectrum are assigned as CH stretching modes of the phenyl ring. The DFT calculations give these modes at 3153, 3099, 3082, 3072, 3049 cm^-1. The benzene ring possesses six ring stretching vibrations, of which the four with the highest wavenumbers (occurring near 1600, 1580, 1490 and 1440 cm^-1) are good group vibrations. With heavy substituents, the bands tend to shift to somewhat lower wavenumbers. In the absence of ring conjugation, the band at 1580 cm^-1 is usually weaker than that at 1600 cm^-1. In the case of C=O substitution, the band near 1490 cm^-1 can be very weak. The fifth ring stretching vibration is active near 1315 ± 65 cm^-1, a region that overlaps strongly with that of the CH in-plane deformation. The sixth ring stretching vibration, or the ring breathing mode, appears as a weak band near 1000 cm^-1, in mono-, 1,3-di- and 1,3,5-trisubstituted benzenes. In the otherwise substituted benzenes, however, this vibration is substituent sensitive and difficult to distinguish from the ring in-plane deformation^26,30 . The υPh modes are expected in the region 1285-1610 cm^-1 for mono substituted benzenes ^26,30.  The DFT calculations give the Ph stretching modes at 1602, 1588, 1498, 1442, 1347 cm^-1. The υPh modes are observed at 1499, 1448, 1350 (IR), 1609 cm^-1 (Raman) for the phenyl ring. The ring-breathing mode of monosubstituted benzenes²⁶ appears near 1000 cm^-1, and the band at 998 cm^-1 theoretically is assigned to this mode. The in-plane CH deformations²⁶ of the phenyl ring are expected above 1000 cm⁻¹ and for the title compound the bands observed at 1255, 1166, 1033 cm⁻¹ in the IR spectrum, 1256, 1170, 1036 cm⁻¹ in the Raman spectrum and at 1251, 1191, 1175, 1091, 1030 cm⁻¹ theoretically are assigned as these modes. Generally, the CH out-of-plane deformations with the highest wavenumbers have a weaker intensity than those absorbing at lower wavenumbers. The stronger γCH band occurring in the region 775 ± 45 cm⁻¹ tends to shift to lower (higher) wavenumbers with increasing electron donating (attracting) power of the substituent, but seems to be more sensitive to mechanical interaction effects. The lowest wavenumbers for this mode are found in the spectra of benzenes substituted with a saturated carbon or heavy atoms such as halogen, sulfur or phosphorus^{30, 41}. The bands at 768 cm⁻¹ in the IR spectrum, 957, 902, 760 cm⁻¹ in the Raman spectrum and the calculated values (DFT) 971, 958, 905, 835, 764 cm⁻¹ are assigned as the out-of-plane CH modes of the phenyl rings. The substituent sensitive modes of the phenyl ring are also identified and assigned (table 1).

First hyperpolarizability

Non-linear optics deals with the interaction of applied electromagnetic fields in various materials to generate new electromagnetic fields, altered in wavenumber, phase or other physical properties⁴². Organic molecules able to manipulate photonic signals efficiently are of importance in technologies such as optical communication, optical computing and dynamic image processing^{43, 44}. Analysis of organic molecules having conjugated π-electron systems and large hyperpolarizability using infrared and Raman spectroscopies has evolved as a subject of research⁴⁵. First hyperpolarizability is a third rank tensor that can be described by a 3 3  3 matrix. The 27 components of the 3D matrix can be reduced to 10 components due to the Kleinman symmetry⁴⁶. The calculated first hyperpolarizability of the title compound is 1.24  10^-30 esu. We conclude that the title compound is an attractive object for future studies of non linear optical properties.

In order to investigate the performance of vibrational wavenumbers of the title compound, the root mean square (RMS) value between the calculated and observed wavenumbers were calculated. The RMS values of wavenumbers were calculated using the following expression^47.

. The RMS error of the observed IR and Raman bands are found to be 23.74, 30.50 for HF and 11.05, 4.58 for DFT methods, respectively. The small differences between experimental and calculated vibrational modes are observed. This is due to the fact that experimental results belong to solid phase and theoretical calculations belong to gaseous phase.

Frontier molecular orbitals

The analysis of the wavefunction indicates that the electron absorption corresponds to a transition from the ground to the first excited state and is mainly described by one electron excitation from the HOMO to LUMO. Both the HOMO and the LUMO are the main orbital taking part in chemical reaction. The HOMO energy characterizes the capability of electron giving; LUMO characterizes the capability of electron accepting⁴⁸. The frontier orbital gap helps to characterize the chemical reactivity, optical polarizability and chemical hardness-softness of a molecule^49. Surfaces for the frontier orbitals were drawn to understand the bonding scheme of the title compound. The calculated HOMO and LUMO energies are -8.393 and -4.542 eV. The chemical hardness and softness of a molecule is a good indication of the chemical stability of the molecule. From the HOMO-LUMO energy gap, one can find whether the molecule is hard of soft. The molecules having large energy gap are known as hard and molecules having a small energy gap are known as soft molecules. The soft molecules are more polarizable than the hard ones because they need small energy to excitation. The hardness value⁴⁸ of a molecule can be determined as η = (-HOMO+LUMO)/2. The value of η of the title molecule is 1.926 eV. Hence we conclude that the title compound belongs to hard material.

Conclusion

The IR and Raman spectra of the title compound were studied. The molecular geometry and wavenumbers were calculated at HF and DFT levels. The observed wavenumbers were found to be in agreement with the calculated (DFT) values. The small differences between experimental and calculated vibrational modes are observed. It must be due to the fact that experimental results belong to solid phase and theoretical calculations belong to gaseous phase. The first hyperpolarizability, infrared intensities and Raman activities are reported.

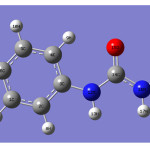Figure 1 Click here to View figure

Table 1: Calculated wavenumbers (scaled), observed IR and Raman bands and assignments.

HF/6-31G*			B3LYP/6-31G*			IRυ(cm-1)	Ramanυ(cm-1)	Assignments
υ(cm-1)	IR intensity	Raman activity	υ(cm-1)	IR intensity	Raman activity
3573	62.46	47.71	3620	40.63	68.22			υasNH2
3465	30.24	84.33	3488	48.00	224.72			υsNH2
3449	73.69	63.59	3475	14.57	11.98	3439		υNH
3088	5.90	51.58	3153	5.87	51.02			υCH
3027	24.75	214.43	3099	25.90	229.84			υCH
3010	37.12	62.01	3082	35.02	75.47			υCH
2999	1.29	89.44	3072	0.541	88.70		3072	υCH
2980	18.87	52.88	3049	20.15	55.58	3035		υCH
1670	392.93	13.08	1667	266.72	16.81	1655	1658	υCO
1637	16.53	0.26	1618	15.77	1.26	1616		δNH2
1617	11.08	48.02	1602	26.55	88.38		1609	υPh
1603	166.85	12.41	1588	122.63	10.74			υPh
1546	487.54	3.67	1526	402.73	10.47	1530		δNH
1502	83.67	1.04	1498	90.91	6.07	1499		υPh
1450	163.38	2.76	1442	159.44	4.18	1448		υPh
1362	203.01	1.90	1347	214.40	2.54	1350		υPh
1317	192.87	1.85	1333	89.53	12.82	1328		δNH
1256	20.86	25.47	1286	61.73	8.92		1290	υCN
1210	6.75	4.15	1251	46.65	47.75	1255	1256	υCN, δCH
1191	2.44	5.88	1191	3.97	8.46			δCH
1147	4.60	6.31	1175	1.01	7.52	1166	1170	δCH, ρNH
1088	8.01	2.96	1091	7.97	3.59			δCH
1074	18.30	6.54	1052	25.22	14.64	1060		τNH2
1058	7.18	0.76	1030	2.88	13.94	1033	1036	δCH
1025	3.07	7.82	998	2.09	33.28		999	υPh
1025	0.41	0.36	995	3.62	0.69			υCN
1004	1.49	20.32	971	0.71	5.19			γCH
973	0.06	13.20	958	0.35	0.14		957	γCH
961	39.11	1.88	905	16.97	2.20		902	γCH
875	1.86	3.85	835	0.67	6.34			γCH
829	1.30	8.00	829	0.04	6.76		829	ωNH
802	340.32	0.20	764	126.95	0.08	768	760	γCH
768	51.08	0.38	724	55.85	0.16			δCO
710	33.64	1.12	695	29.46	1.34		701	γPh
682	2.43	3.47	679	1.10	5.32		682	γCO
627	1.42	4.07	627	1.37	3.81	622	628	δPh
602	32.40	1.63	588	62.26	2.62		590	δPh
562	20.86	3.37	556	16.74	2.69		548	γNH
552	334.21	2.18	533	40.92	3.82			ωNH2
519	47.15	1.32	502	292.37	0.49	502	502	γPh
420	0.87	0.16	412	0.46	0.12	416	414	τCONH2
358	1.07	2.93	358	1.06	3.31			γPh
337	4.41	2.25	339	1.99	3.31			δPh(X)
331	15.23	2.20	291	24.41	3.28			γPh(X)
235	0.29	3.12	220	4.10	2.04			δPh(X)
175	12.20	0.24	177	10.24	0.34			γPh(X)
79	6.48	1.07	74	3.35	1.03			tPh
37	13.85	1.05	50	14.76	0.72			tPh

υ-stretching; δ-in-plane deformation; γ-out-of-plane deformation; t-torsion; τ-twisitng; as-asymmetric; sy-symmetric; Ph-phenyl ring; X-substituent sensitive.

References

1. Katrizky, A.R., Advances in Heterocyclic Chemistry, Academic Press, New York,     (1983).
2. Castro, M., Cruz, J., Otazo-Sanchez, E., Perez-Marın, L., J. Phys. Chem. A 107: 9000 (2003).
3. Amer, J.,  Soc. Hort. Sci. 117: 85 (1992).
4. Zhang, Z .,Spectrochim. Acta .69: 65 (2007).
5. Klementova, S., Zemanova, M., Res. J. Chem. Environ. 12: 4 (2008).
6. Hamza, A., Schubert, G., Soos, T., Papai, I., J. Am. Chem. Soc. 128: 13151 (2006).
7. Yang, W., Zhou, W., Zhang, Z., J. Mol. Struct. 828: 46 (2007).
8. Badawi, H.M., Spectrochim. Acta 72: 523 (2009).
9. Zhang, N., Jiang, M. H ., Yuan, D.R., Xu, D.,Tao, X.T., Shao, Z.S.,  J. Cryst.Growth, 102: 580 (1990).
10. Ushasree, P.M., Muralidharan, R., Jayavel, R., Ramasamy, P., J. Cryst. Growth, 218: 365 (2000).
11. Qussaid, M., Becker, P., Nedelec, C.C., Phys. Stat. Sol. 207: 499 (1998).
12. Marcy, H.O., Warren, L.F., Webb, M.S.,  Ebbers, C.A., Velsko, S.P., Kennedy, G.C., Catella, G. C., Appl. Opt. 31: 5051 (1992).
13. Selvaraju, K., Valluvan, R., Kumararaman,S., Mater. Lett. 60: 3130 (2006).
14. Selvaraju, K., Valluvan, R., Kumararaman,S., Mater. Lett. 61: 751 (2007).
15. Pfeffer, F.M., Gunnlaugsson, T., Jensen, P., Kruger, P.E., Org.  Lett. 7: 5357 (2005).
16. Beer, P.D., Gale, PA., Angew. Chem. Int. Ed. 40: 486 (2001).
17. Koulov, A.V., Mahoney, J.M., Smith, B.D., Org. Biomol. Chem. 1: 27 (2003).
18. Gunnlaugsson, T., Ali, H.D.P., Glynn, M., Kruger, P.E., Hussey, G.M., Pfeffer, F.M., Dos Santos, C.M.G., Tierney, J., J. Fluoresc. 15: 287 (2005).
19. Kim, S.K., Singh, N.J., Kim, S.J., Swamy, K.M.K., Kim, S.H., Lee, K.H., Kim, K.S.,Yoon, J., Tetrahedron 61: 4545 (2005).
20. Hay, B.P., Firman, T.K., Moyer, B.A., J. Am. Chem. Soc. 127: 1810 (2005).
21. Frisch, M.J., et al, Gaussian 09, Revision B.01, Gaussian, Inc., Wallingford CT (2010)
22. Foresman, J.B., in: Frisch,E., (Ed.) Exploring Chemistry with Electronic Structure Methods: A Guide to using Gaussian, Pittsburg, PA, (1996).
23. Dennington, R., Keith, T., Millam, J., Gaussview, Version 5, Semichem Inc. ShawneeMissionKS (2009).
24. Socrates,G.  Infrared Characteristic Group Frequencies, John Wiley and Sons: New York (1981).
25. Lin, C., Wu, K., Chem. Phys. Lett. 321: 83 (2000).
26. Roeges, N.P.G., A Guide to the Complete Interpretation of the Infrared Spectra of Organic Structures, Wiley, New York (1994)
27. Barthes, M., De Nunzio, G., Ribet, G., Synth. Met. 76: 337 (1996).
28. El‐Asmy, A.A., Al‐Hazmi, .G.A., Spectrochim. Acta 71: 1885 (2009).
29. Colthup, N.B., Daly, L.H., Wiberly, S.E., Introduction to Infrared and Raman Spectroscopy, third ed. Academic Press, Boston, MA (1990).
30. Varsanyi, G. Assignments of Vibrational Spectra of Seven Hundred Benzene Derivatives, Wiley, New York (1974).
31. El‐Shahawy, A.S., Ahmed, S.M., Sayed, N.K., Spectrochim. Acta 66: 143 (2007).
32. Panicker, C.Y., Varghese, H.T., Thansani, T., Turk. J. Chem. 33: 1 (2009).
33. Varghese, H.T., Panicker, C.Y.,Anto, P.L., Philip, D., J. Raman Spectrosc. 37: 487 (2006).
34. Anto, P.L., Panicker, C.Y., Varghese, H.T., Philip, D. J. Raman  Spectrosc. 37: 1265 (2006).
35. Wojciechowski, P.M., Michalska, D., Spectrochim. Acta 68: 948 (2007).
36. Sundaraganesan, N., Saleem, H., Mohan, S., Ramalingam, M., Spectrochim. Acta   61: 377 (2005).
37. Krishnakumar, V., Balachandran, V., Spectrochim. Acta  61: 1811 (2005).
38. Altun, A., Golcuk, K., Kumru, M., Vib. Spectrosc. 31: 215 (2003).
39. Kurt, M., Yurdakul, M., Yurdakul, S., J. Mol. Struct. (THEOCHEM), 711: 25 (2004).
40. Tzeng, W.B., Narayanan, K., Shieh, K.C., Tung, C.C., J. Mol. Struct. (THEOCHEM),  428: 231 (1998).
41. Colthup, N.B., Appl. Spectrosc. 30: 589 (1976).
42. Shen, Y.R., The Principles of Nonlinear Optics, Wiley, New York (1984).
43. Kolinsky, P.V., Opt. Eng. 31: 1676 (1992).
44. Eaton, D.F., Science 253: 281 (1991).
45. Tommasini, M., Castiglioni, C., Del Zoppo, M., Zerbi, G., J. Mol. Struct. 480: 179 (1999).
46. Kleinman, D.A., Phys. Rev. 126: 1977 (1962).
47. Joseph, T., Varghese, H.T., Panicker, C.Y., Viswanathan, K., Sundaraganesan,N., Subramanin, N., Dolezal, M., Global J. Anal. Chem. 3: 1 (2012).
48. Fukui, K. Science 218: 747 (1982).
49. Kosar, B., Albayrak, C., Spectrochim. Acta 78A: 160 (2011).

 

---

This work is licensed under a Creative Commons Attribution 4.0 International License.