FT-IR, FT-Raman and Computational Study of P-Acetylbenzonitrile

Introduction

The benzonitrile moiety is a relevant polar group in molecules present in calamitic and linear and nonlinear optical materials^1-4. Several molecular properties, such dipole moment, polarizability (dynamic and static), polarizability anisotropies, and nonlinear optical properties are currently explored in benzonitrile, both experimental and theoretical methods². At room temperature, the certain benzonitrile derivative crystals mainly showed locally excited fluorescence⁵. The importance of cyano-substituted aromatic compounds in molecular electronic devices and new kinds of mesogenic materials has renewed the interest in their chemical and electronic properties^6. Alvarado et al.⁷ reported the solvent effect on the electronic polarizability of benzonitrile. In the present study the FT-IR, FT-Raman and theoretical calculations of the wavenumbers of the title compound are reported.

Experimental

The FT-IR spectrum was recorded using a DR/Jasco FT-IR 6300 spectrometer. The spectral resolution was 2 cm^-1.  The FT-Raman spectrum was obtained on a Bruker RFS 100/s, Germany. For excitation of the spectrum the emission of Nd:YAG laser was used, excitation wavelength 1064 nm, maximal power 150 mW.

Computational Details

Calculations of the title compound were carried out with Gaussian09 software program⁸ using the HF/6-31G* and B3LYP/6-31G* basis sets to predict the molecular structure and vibrational wavenumbers.  The DFT hybrid B3LYP functional method tends to overestimate the fundamental modes; therefore scaling factors have to be used for obtaining a considerably better agreement with experimental data^9. The wavenumber values computed contain known systematic errors and we therefore, have used the scaling factor values of 0.8929 and 0.9613 for HF and DFT basis sets^9.  The assignment of the calculated wavenumbers is aided by the animation option of Gaussview program, which gives a visual presentation of the vibrational modes¹⁰.

Results and Discussion

IR and Raman spectra

The observed IR, Raman and calculated (scaled) wavenumbers and assignments are given in Table 1. The C=O stretching mode¹¹ is expected in the region 1750-1650 cm^-1 and Ghosh et al.,¹² reported υ(C=O) at 1683 cm^-1 and Hosny¹³ reported this mode at   1662 cm^-1. These bands are observed at 1648 cm^-1 in the IR spectrum and at 1629 cm^-1 theoretically (DFT) for the title compound. The δ(C=O) in-plane deformation and the out-of-plane deformation γ(C=O) are expected in the regions 625 ± 70 and 540 ±8 0 cm^-1, respectively¹¹. The bands observed at 643, 533 cm^-1 in the IR spectrum and 652 cm^-1 in the Raman spectrum  are assigned as C=O deformation modes. The theoretically calculated values are 648 and 524 cm^-1. Mohammed and EL-Glamel¹⁴ reported the deformation band of C=O at 623 cm^-1.

Nitrogen compounds featuring triple or cumulated double bonds, such as cyanides or nitriles (–C≡ N) and cyanates –O–(C≡N), all provide a unique spectrum, typically with a single, normally intense absorption at 2280–2200 cm⁻¹ (for cyano compounds) and 2285–1990 cm⁻¹ (for cyanates, isocyanates and thiocyanates)^11,14. In the present case the stretching mode υC≡N is observed at 2253 cm⁻¹ in the IR spectrum and at 2231 cm^-1 in the Raman spectrum and the calculated value (DFT) for this mode is 2213 cm^-1. The in-plane and out-of-plane deformation bands of C≡N are also identified and assigned (table 1).

The asymmetric stretching vibrations of CH₃ are expected in the range 2950-3050 cm^-1 and symmetric CH₃ vibrations in the range^11,15 of 2900-2950 cm^-1. The first of this results from the asymmetric stretching υ_asCH₃ mode in which two C-H bonds of the methyl group are extending while the third one is contracting. The second arises from the symmetrical stretching υ_sCH₃ in which all three of the C-H bonds extend and contract in phase. The asymmetric stretching modes of the methyl group are calculated (DFT) to be 3054, 2995 cm^-1 and the symmetric mode at 2933 cm^-1. The bands observed at 3043 in the IR spectrum and at 2939 cm^-1 in the Raman spectrum are assigned as stretching modes of the methyl group. Two bending can occur within a methyl group. The first of these, the symmetrical bending vibration, involves the in-phase bending of the C-H bonds. The second, the asymmetrical bending vibration, involves out-of-phase bending of the C-H bonds. The asymmetrical deformations are expected¹¹ in the range 1400-1485 cm^-1. The calculated values (DFT) of δ_asCH₃ modes are at 1466, 1453   cm^-1. In many molecules, the symmetric deformations δ_sCH₃ appears with an intensity varying from medium to strong and expected in the range¹¹ 1380±25 cm^-1. The band observed at 1372 cm^-1 in the IR spectrum is assigned as the δ_sCH₃ mode. The DFT calculations give δ_sCH₃ mode at 1384 cm^-1. Aromatic molecules display a methyl rock¹¹ in the neighborhood 1045 cm^-1. The second rock¹² in the region 970 ± 70 cm^-1 is more difficult to find among the C-H out-of-plane deformations. In the present case, these ρCH₃ modes are calculated at 1040 and 996 cm^-1. The methyl torsions¹¹ often assigned in the region 185 ± 65 cm^-1.

The benzene ring possesses six ring stretching modes, of which the four with the highest wavenumbers (occurring near 1600, 1580, 1490 and 1440 cm^-1) are good group vibrations^11. With heavy substituents, the bands tend to shift to somewhat lower wavenumbers. In the absence of ring conjugation, the band at 1580 cm^-1 is usually weaker than at 1600 cm^-1. In the case of C=O substitution, the band near 1490 cm^-1 can be very weak. The fifth ring stretching mode is active near 1315 ± 65 cm^-1, a region that overlaps strongly with that of the CH in-plane deformation. The sixth ring stretching mode or the ring breathing mode, appears as a weak band near 1000 cm^-1 in mono-, 1,3-di and 1,3,5-trisubstitued benzenes^11. In the otherwise substituted benzenes, however, this mode is substituent sensitive and difficult to distinguish from the ring in-plane deformation^11. For the para-substituted phenyl ring the υPh modes are expected in the range¹² 1280–1620 cm^−1. For the title compound, the υPh modes are observed at 1604, 1556, 1494, 1401, 1317 cm⁻¹ (IR), 1609 cm^-1 (Raman) and 1600, 1543, 1499, 1403, 1322 cm^-1 theoretically. The ring breathing mode of the para substituted benzenes with entirely different substituents¹⁶ has been reported in the interval 780-880 cm^-1. and in the present case the band at 781 cm^-1, 792 cm^-1 in Raman and 786 cm^-1 (DFT) is assigned as the ring breathing mode of Phenyl ring. The in-plane bending δCH modes¹¹ of the phenyl ring are expected above 1000 cm^-1. Bands observed at 1263, 1115, 1010 cm^-1 in the IR spectrum and at 1304, 1268 cm^-1, in the Raman spectrum are assigned as δCH modes of the para-substituted benzene ring. The DFT calculations give these modes at 1306, 1259, 1118, 1015 cm^-1. The CH out-of-plane deformations¹¹ are observed between 1000 and 700 cm^-1. Generally, the CH out-of-plane deformations with the highest wavenumbers have a weaker intensity than those absorbing at lower wavenumbers. These γCH modes are observed at 963, 853 cm^-1 (IR), 832 cm^-1 (Raman), 971, 953, 860, 841 cm^-1 (DFT) for phenyl ring. The strong CH out-of-plane deformation band occurring at 840 ± 50 cm^-1 is typical for para-substituted benzenes^11. For the title compound, a band is observed at 853 cm^-1 in the IR spectrum, which finds support from the computational result, 860 cm^-1 with high calculated IR intensity. The substituent sensitive modes of the phenyl ring are also identified and assigned (table 1).

First hyperpoplarizability

Non-linear optics deals with the interaction of applied electromagnetic fields in various materials to generate new electromagnetic fields, altered in wavenumber, phase or other physical properties¹⁷. Many organic molecules, containing conjugated π electrons and characterized by large values of molecular first hyperpolarizabilities, were analyzed by means of vibrational spectroscopy^18,19. Analysis of organic molecules having conjugated π-electron systems and large hyperpolarizability using infrared and Raman spectroscopies has evolved as a subject of research²⁰. Organic molecules able to manipulate photonic signals efficiently are of importance in technologies such as optical communication, optical computing and dynamic image processing^18,19. First hyperpolarizability is a third rank tensor that can be described by a 3 3  3 matrix. The 27 components of the 3D matrix can be reduced to 10 components due to the Kleinman symmetry²¹. The calculated first hyperpolarizability of the title compound is 3.62  10^-30 esu.. We conclude that the title compound is an attractive object for future studies of non linear optical properties.

In order to investigate the performance of vibrational wavenumbers of the title compound, the root mean square (RMS) value between the calculated and observed wavenumbers were calculated. The RMS values of wavenumbers were calculated using the following expression²².

 . The RMS error of the observed IR and Raman bands are found to 30.49, 37.51 for HF and 11.54, 9.49 for DFT methods, respectively. The small differences between experimental and calculated vibrational modes are observed. This is due to the fact that experimental results belong to solid phase and theoretical calculations belong to gaseous phase.

Frontier molecular orbitals

The analysis of the wavefunction indicates that the electron absorption corresponds to a transition from the ground to the first excited state and is mainly described by one electron excitation from the HOMO to LUMO. Both the HOMO and the LUMO are the main orbital taking part in chemical reaction. The HOMO energy characterizes the capability of electron giving; LUMO characterizes the capability of electron accepting²³. The frontier orbital gap helps to characterize the chemical reactivity, optical polarizability and chemical hardness-softness of a molecule²⁴. Surfaces for the frontier orbitals were drawn to understand the bonding scheme of the title compound. The calculated HOMO and LUMO energies are -9.509 and -5.751 eV. The chemical hardness and softness of a molecule is a good indication of the chemical stability of the molecule. From the HOMO-LUMO energy gap, one can find whether the molecule is hard of soft. The molecules having large energy gap are known as hard and molecules having a small energy gap are known as soft molecules. The soft molecules are more polarizable than the hard ones because they need small energy to excitation. The hardness value²³ of a molecule can be determined as η = (-HOMO+LUMO)/2. The value of η of the title molecule is 1.879 eV. Hence we conclude that the title compound belongs to hard material.

Conclusion

The IR and Raman spectra of the title compound have been recorded and analyzed. The harmonic vibrational wavenumbers were calculated theoretically using Gaussian09 software package. Calculations were performed by HF and DFT levels using the standard 6-31G* basis sets. The calculated wavenumbers (DFT) agree well with the observed wavenumbers. The data obtained from vibrational wavenumber calculations are used to assign vibrational bands found in the IR and Raman spectra of the title compound. The predicted infrared intensities, Raman activities and first hyperpolarizability are reported.

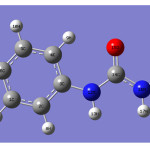Figure 1  Click here to View figure

Table 1: Calculated (scaled) wavenumbers, observed IR, Raman bands and assignments.

HF/6-31G*			B3LYP/6-31G*			IRυ(cm-1)	Ramanυ(cm-1)	Assignments
υ(cm-1)	IRI	RA	υ(cm-1)	IRI	RA
3051	1.24	96.68	3118	2.05	133.59			υCH
3041	6.24	90.50	3112	7.06	71.42			υCH
3028	2.76	55.52	3101	1.80	54.71			υCH
3023	4.24	42.40	3096	3.61	39.79	3087	3085	υCH
2968	10.01	104.40	3054	10.26	106.32	3043		υasCH3
2919	11.00	50.62	2995	8.81	50.20			υasCH3
2860	3.24	109.37	2933	2.57	117.90		2939	υsCH3
2279	41.74	367.68	2213	20.88	560.76	2253	2231	υC≡N
1687	204.73	57.86	1629	101.41	23.29	1648		υC=O
1628	11.19	256.48	1600	32.17	424.81	1604	1609	υPh
1567	13.02	2.66	1543	12.70	12.20	1556		υPh
1514	1.96	0.26	1499	0.62	0.77	1494		υPh
1462	16.77	26.02	1466	15.12	27.62			δasCH3
1453	17.29	13.50	1453	18.65	11.50			δasCH3
1407	59.58	5.16	1403	34.55	5.80	1401		υPh
1398	0.56	1.44	1384	25.51	5.72	1372		δsCH3
1328	4.70	2.93	1322	4.68	2.57	1317		υPh
1261	199.62	30.02	1306	8.22	0.59		1304	δCH
1208	31.54	1.69	1259	222.02	48.81	1263	1268	δCH
1194	3.34	3.10	1198	6.48	3.52	1192		υCC
1180	6.09	56.42	1185	7.74	81.04	1175	1182	υCC
1110	0.04	0.16	1118	4.86	0.14	1115		δCH
1080	3.35	26.68	1074	1.79	37.79	1071	1073	υCC
1067	0.55	8.22	1040	1.27	3.477	1030		ρCH3
1049	1.00	0.63	1015	5.95	1.15	1010		δCH
1032	0.01	0.99	996	0.53	0.91			ρCH3
1018	5.58	0.08	971	0.10	1.46			γCH
960	25.35	1.17	953	32.27	5.92	963		γCH
898	51.72	2.26	860	34.34	3.26	853		γCH
883	27.14	1.43	841	21.72	2.41		832	γCH
781	2.31	26.01	786	1.22	25.94	781	792	υPh
763	0.08	4.37	745	0.01	1.51		731	γPh
651	0.63	4.45	648	0.80	4.93	643	652	δC=O
631	13.50	2.50	635	10.01	1.07			δC≡N
607	36.10	1.07	598	19.02	0.64	599		δPh(X)
562	4.51	3.26	554	5.72	0.70	560		γC≡N
547	2.59	10.60	539	3.36	6.20	533	536	γPh(X)
526	25.93	4.58	524	13.42	4.55	533		γC=O
433	1.02	2.46	436	0.95	2.36			δPh(X)
416	0.04	0.20	407	0.01	0.09			δPh(X)
401	0.22	5.05	392	0.11	3.22			γPh(X)
313	0.32	5.43	315	0.31	5.58		329	γPh(X)
226	6.09	0.44	223	4.86	0.20		219	tC≡N
209	0.76	0.15	204	0.89	0.186			tPh
165	0.15	0.02	161	0.36	0.06		170	tCH3
132	8.91	3.66	128	7.16	3.58		140	tC=O
79	7.15	0.76	77	6.89	0.61			tPh
53	4.23	1.46	68	1.79	1.45			tPh

υ-stretching; δ-in-plane deformation; γ-out-of-plane deformation; t-torsion; Ph-phenyl ring; X-substituent sensitive; as-asymmetric; s-symmetric.

Reference

1. Howard, S., Fallis, I., Willock, D., Mol. Phys., 97: 913 (1999).
2.  Navard, P., Flory, P., J. Chem. Soc., Faraday Trans., 82: 3367 (1986).
3. Flory, P., Navard, P., J. Chem. Soc., Faraday Trans.,  82: 3381 (1986).
4. Kumar, P., Pisipati,V., Rajeswari, A.,  Sreehari, S., Z. Naturforsch. 57: 184 (2002).
5. Druzhinin, S., Demeter, A., Zachariasse, K.A., Chem. Phys. Lett. 347: 421 (2001).
6. Czechowski, G., Ziolo, J., Rzoska, S., Paluch, M., Z. Naturforsch, 57: 244 (2002).
7. Alvardo, Y.J., Labarca, P.H., Cubillan, N., Osorio, E., Karam, A., Z. Naturforsch,              58: 68(2003).
8. Frisch, M.J., et al, Gaussian09, Revision B.01., Gaussian Inc., Wallingford CT (2010).
9. Foresman, J.B., Frisch, E., Exploring Chemistry with Electronic Structure Methods, A Guide to using Gaussian, Pittsburg, PA (1996).
10. Gaussview Version 5, Dennington, R., Keith, T., Millam, J., Semichem Inc. ShawneeMissionKS (2009).
11. Roeges, N.P.G., A Guide to the Complete Interpretation of Infrared Spectra of Organic Structures, Wiley, New York (1994).
12. Ghosh, T., Bhattacharya, S., Das, A., Mukherjee,G., Drew, M.G.B., Inorg. Chim. Acta. 358: 989 (2005).
13. Hosny, N.M., J. Mol. Struct.  923: 98 (2009).
14. Mohamed, G.G., El-Gamel, N.E.A., Spectrochim Acta  60: 3141(2004).
15. Colthup, N.B., Daly, L.H., Wiberly, S.E., Inroduction to Infrared and Raman Spectroscopy, third ed., Academic Press, Boston (1990).
16. Varsanyi, G., Assignments of Vibrational Spectra of Seven Hundred Benzene Derivatives, Wiley: New York (1974).
17. Shen, Y.R., The Principles of Nonlinear Optics, Wiley, New York (1984).
18. Kolinsky, P.V., Opt. Eng. 31: 1676 (1992).
19. Eaton, D.F., Science 253: 281 (1991).
20. Tommasini, M., Castiglioni, C., Del Zoppo, M., Zerbi, G., J. Mol. Struct. 480: 179 (1999).
21. Kleinman, D.A., Phys. Rev. 126: 1977 (1962).
22. Joseph, T., Varghese, H.T., Panicker, C.Y., Viswanathan, K., Sundaraganesan, Subramanina, N., Dolezal, M., Global J. Anal. Chem. 3 :1 (2012).
23. Fukui, K., Science 218 : 747 (1982).
24.  Kosar, B., Albayrak, C., Spectrochim. Acta 78A : 160 (2011).

---

This work is licensed under a Creative Commons Attribution 4.0 International License.