A DFT Study of Solvation Effects on Tautomerism of 6-oxo Purine by Polarisable Continuum Method (PCM)

Introduction

Tautomerism interconversions ^1,2. have been investigated by chemists during last decades. Recently, study of tautomerism received renewed attention due to its importance on the determination of compounds properties and their area of applications. The importance of tautomerism is revealed more since in recent years the investigation about tautomerism has been the major topic in theoretical chemistry. For example, tautomerism in keto-enol ^3,4., imine–enamine ^5,6., purine ⁷., pirimidine ⁸. and many other systems ⁹. have been studied during the past decades. Thereupon, compounds containing different tautomers can be the subject of interest by theoretical chemists ¹⁰. Purine bases and their thio derivatives are found in many biological systems and they are very important from clinical point of view. For example, 6-thiopurine (THIOP) is one of the purine analogues most commonly used in the treatment of the acute human leukaemia ¹¹. It is also known that 6-thiopurine derivatives, among them 2-amino-6- thiopurine has interesting chemotherapy effects, including powerful antitumoral activity ¹². The oxopurines are of biological importance, because they are metabolic intermediate products of purine metabolism formed by degradation of nucleic acids. Hypoxanthine (1,7-dihydro-6H-purin-6-one) occasionally occurs as a constituent of the nucleoside inosine in minor amounts in transfer RNA ¹³ and is oxidized to xanthine and uric acid in man, these reactions being catalyzed by the molybdenum- and iron-containing enzyme xanthine oxidase. Defects in purine metabolism result in an increase in the uric acid level and in the deposition of sodium hydrogen urate monohydrate crystals in joints. This disease, known as gout, is clinically treated by the allopurinol, which has also been used in conjunction with anticancer drugs, combined with 6-mercaptopurine in treatment of leukemia ^14,15. Enzymes attack purines at preferred positions and, therefore, the tautomerization of the purine molecules may play an important role in the replication process and spontaneous mutation, and the equilibrium is strongly sensitive to the interaction of these molecules with their environment ¹⁶. In equilibrium, oxopurine bases exist in different tautomeric forms, the protropic tautomerism occurring in both rings (pyrimidine and imidazole); thus two types of equilibria can be observed: keto ↔ enol and N(7)H ↔N(9)H. Knowledge of the various geometric and electronic structures as well as the relative stability of tautomeric forms provides a basis for understanding biological activity of oxopurine bases. In addition, knowing how these tautomerization energies change in different environments can provide insight into the influence of solvent effects on molecular stability. The physicochemical properties of the tautomerism of hypoxanthine have been investigated experimentally ^17-27 and theoretically ^28-32. In a wide variety of environments, including the gas phase, keto tautomers of hypoxan thine are most stable. This conclusion is supported by results of UV ^19,21, IR ^17,18, Raman ²⁹, 1H NMR¹⁹ and 13C NMR ^19,23 spectroscopies, and X-ray analysis ²⁴. Pullman and Pullman ²⁸ have investigated the tautomerism of oxopurines by the theoretical CNDO/2 method and three groups of authors ^29-31 have reported ab initio quantum mechanical calculations using 6-31G(d), 6-31G(d,p), or MIDI basis sets. Contreras and Alderete ³² used the semiempirical AM1 and MNDO methods to calculate the structure, bondorder matrices, localized MOs, and IR spectra for the tautomers of hypoxanthine in the gas phase.

Computational methods

All these calculations were carried out on a core i7 personal computer by means of GAUSSIAN09 program package. First, all the compounds structures were drawn using Gauss View 03 and optimized in GAUSSIAN09. The tautomers were also optimized in solvents according to the polarisable continuum method of Tomasi and co-workers, which exploits the generating polyhedra procedure ^33-37 to build the cavity in the polarisable continuum medium, where the solute is accommodated. Atomic charges in all the structures were obtained using the Natural Population Analysis (NPA) method within the Natural Bond Orbital (NBO) approach. ³⁸

Results and discussion

Gas phase

Structures and numbering of  6-oxo purine  are depicted in Figure 1. and the results of energy comparisons of six tautomers in the gas phase and different solvents are given in Table 1. In the gas phase OP2 form is more stable than the other forms. The most and the least differences between OP2 and the other forms in gas phase are found for OP3 amd OP1 with 20.999 kcal mol^-1 and 0.302 kcal mol^-1  respectively(Table 2). The order of stability of all the tautomers in the gas phase is OP2 > OP1 > OP6> OP5> OP7 >OP4 >OP3. The calculated dipole moments for all forms are presented in Table 3. OP2 tautomer has the smallest dipole moments than the other seven forms with 1.733 D.  OP5 tautomer with has the largest dipole moments with 5.0271D in water. The major difference of dipole moment belongs to OP3 form with 3.5453D in gas and water phase. The calculated values NBO charges using the natural population analysis (NPA) of optimized structures of 6-oxo purine  tautomers in the gas phase and solvents are listed in Table 3. In OP1 form, N9 atom carries the largest negative charge, in OP1, OP2 nitrogen atoms at position 1 and 9 carry the largest negative charge, carbon atoms at position 2 or 6 carry the largest positive charge and these positions will most effectively interact with nucleophiles.

Solvent effects

Solvent effects are relevant in tautomers stability phenomena, since polarity differences among tautomers can induce significant changes in their relative energies in solution. PCM/B3LYP calculations were used to analyze the solvent effects on tautomerism of 6-oxo purine . It is important to stress that the PCM model does not consider the presence of explicit solvent molecules; hence specific solute–solvent interactions are not described and the calculated solutions effects arise only from mutual solute–solvent electrostatic polarization. The data presented in Table 1. show that polar solvents increase the stability of all 6-oxo purine tautomers in compare to gas phase. The difference between the total energies of 6-oxo purine and the other forms shows a regular trend when changing from gas phase to more polar solvents (water). In solvent and gas non-polarisable phases and benzene OP2 is more stable than other forms, but in polarisable solvents like methanol and water OP1 form is more stable than other forms. The order of stability of all the tautomers in gas phase is OP2 > OP1> OP6> OP5> OP7> OP4 >OP3, and for benzene (non-polarisable solvent) the order of stability is OP2> OP1> OP2> OP4> OP5> OP7 >OP3 and for polarisable solvents (THF, methanol and water the order of stability is OP2> OP1> OP4> OP6> OP5> OP7 >OP3. Total energy shows a regular trend by changing the gas phase to the solution, polarisable solvents increase  tautomeric stability compared with gas phase. Based on Table 4.  The dipole moments increase by changing the gas phase to the solution as well as by increasing the solvent polarity. The highest dipole moment belongs to OP3 in water solvent by 14.0383 D and the biggest difference of dipole moment is for water anad gas phases by 3.5453 D. The least dipole moment  amount for all the forms in all phases belongs to OP2 by 1.7388 D. We have examined the charge distribution of  tautomers in the solvent as well as gas phase by using calculated NBO charges. The charge distribution in solvents with increase of polarity differently varies for any atoms.

Conclusion

In the gas phase and benzene (non-polarisable solvent) OP2 form is more stable than the other forms but in polarisable solvents OP1 is the most stabilized form. With increase of polarity total energy of all compounds were more negative.

The charges on all nine positions were affected by solvents. In addition with increase of dielectric constant a variation was found.

The dipole moments of all compounds are affected by solvent. With increase of the polarity of solvents the dipole moments of all tautomers were increased.

Table 1: Total energies^a at B3LYP/6-311++G**  in the gas phase and solvents

Tautomer	Gas(1.0)	Benzene(2.2)	THF(7.6)	Methanol(33)	Water(78.4)
OP1	-487.2231411	-487.2329258	-487.239179	-487.2411882	-487.2418963
OP2	-487.2236231	-487.2330175	-487.2388823	-487.2410176	-487.2413929
OP3	-487.1901589	-487.2063456	-487.2176399	-487.2220135	-487.2227977
OP4	-487.2108888	-487.2215486	-487.2283369	-487.2308381	-487.2312795
OP5	-487.2152685	-487.2223519	-487.2267134	-487.2282954	-487.2285733
OP6	-487.2171955	-487.2240913	-487.2228308	-487.2298283	-487.2300949
OP7	-487.2123809	-487.2203886	-487.2255124	-487.2270985	-487.2277453

^aHartree.

Table 2: Energy^a  difirrence between the tautomers of 6-oxo purine

Tautomer	Gas(1.0)	Benzene(2.2)	THF(7.6)	Methanol(33)	Water(78.4)
OP1	0.0004820	0.0000917	0.0000000	0.0000000	0.0000000
OP2	0.0000000	0.0000000	0.0002967	0.0001706	0.0005034
OP3	0.0334642	0.0266719	0.0215391	0.0191747	0.0190986
OP4	0.0127343	0.0114689	0.0108421	0.0103501	0.0106168
OP5	0.0083546	0.0106656	0.0124656	0.0128928	0.0133230
OP6	0.0064276	0.0089262	0.0163482	0.0113599	0.0118014
OP7	0.0112422	0.0126289	0.0136666	0.0140897	0.014151

^aHartree.

Table 3: calculated NBO charge on ring atoms of 6-oxo purine

Tautomer	Atom	Gas	Benzene	THF	Methanol	DMSO	Water
OP1	N1	-0.6160	-0.6531	-0.6506	-0.6496	-0.6495	-0.6495
	C2	0.3381	0.3392	0.3438	0.3456	0.3457	0.3459
	N3	-0.5437	-0.5737	-0.5774	-0.5784	-0.5785	-0.5786
	C6	0.5231	0.6862	0.6869	0.6870	0.6870	0.6870
	N7	-0.2321	-0.5200	-0.5374	-0.5440	-0.5446	-0.5452
	C8	0.1324	0.2591	0.2643	0.2663	0.2665	0.2667
	N9	-0.6732	-0.5940	-0.5906	-0.5892	-0.5891	-0.5890
OP2	N1	-0.6242	-0.6493	-0.6465	-0.6454	-0.6453	-0.6452
	C2	0.3329	0.3258	0.3305	0.3323	0.3324	0.3326
	N3	-0.4848	-0.5454	-0.5587	-0.5637	-0.5642	-0.5646
	C6	0.5143	0.6698	0.6724	0.6733	0.6734	0.6735
	N7	-0.5902	-0.5710	-0.5677	-0.5664	-0.5663	-0.5662
	C8	0.1949	0.2784	0.2831	0.2848	0.2850	0.2851
	N9	-0.4943	-0.5502	-0.5663	-0.5723	-0.5729	-0.5734
OP3	N1	-0.4762	-0.5930	-0.6124	-0.6197	-0.6203	-0.6210
	C2	0.3174	0.3338	0.3420	0.3451	0.3454	0.3457
	N3	-0.5343	-0.6269	-0.6182	-0.6146	-0.6143	-0.6139
	C6	0.5015	0.6656	0.6664	0.6662	0.6662	0.6662
	N7	-0.2353	-0.5106	-0.5317	-0.5399	-0.5406	-0.5413
	C8	0.1169	0.2493	0.2569	0.2600	0.2603	0.2606
	N9	-0.5401	-0.6103	-0.6032	-0.6003	-0.6000	-0.5998
OP4	N1	-0.4715	-0.6013	-0.6173	-0.6233	-0.6238	-0.6243
	C2	0.3325	0.3379	0.3434	0.3455	0.3456	0.3458
	N3	-0.5071	-0.6090	-0.6038	-0.6018	-0.6016	-0.6014
	C6	0.4967	0.6534	0.6545	0.6546	0.6546	0.6546
	N7	-0.5821	-0.5661	-0.5646	-0.5641	-0.5640	-0.5640
	C8	0.2020	0.2781	0.2840	0.2863	0.2866	0.2868
	N9	-0.5616	-0.5728	-0.5804	-0.5828	-0.5830	-0.5832
OP5	N1	-0.5251	-0.5893	-0.6000	-0.6041	-0.6044	-0.6048
	C2	0.3186	0.3078	0.3054	0.3043	0.3042	0.3041
	N3	-0.5497	-0.5698	-0.5731	-0.5741	-0.5742	-0.5743
	C6	0.5496	0.6251	0.6245	0.6241	0.6241	0.6241
	N7	-0.2799	-0.5550	-0.5628	-0.5655	-0.5658	-0.5660
	C8	0.1395	0.2824	0.2889	0.2915	0.2918	0.2920
	N9	-0.6435	-0.6051	-0.6017	-0.6004	-0.6003	-0.6001
OP6	N1	-0.5733	-0.6226	-0.6258	-0.6270	-0.6271	-0.6272
	C2	0.3230	0.3093	0.3080	0.3074	0.3074	0.3074
	N3	-0.5478	-0.5698	-0.5736	-0.5748	-0.5749	-0.5750
	C6	0.5466	0.6272	0.6264	0.6259	0.6259	0.6258
	N7	-0.2552	-0.5310	-0.5455	-0.5508	-0.5513	-0.5517
	C8	0.1338	0.2782	0.2846	0.2870	0.2873	0.2875
	N9	-0.6469	-0.6062	-0.6025	-0.6010	-0.6009	-0.6008
OP7	N1	-0.5647	-0.6101	-0.6135	-0.6146	-0.6147	-0.6148
	C2	0.3218	0.2973	0.2960	0.2954	0.2953	0.2953
	N3	-0.4948	-0.5417	-0.5555	-0.5607	-0.5612	-0.5616
	C6	0.5341	0.6035	0.6071	0.6086	0.6087	0.6089
	N7	-0.5909	-0.5879	-0.5827	-0.5807	-0.5805	-0.5803
	C8	0.1814	0.2939	0.3002	0.3025	0.3027	0.3029
	N9	-0.4985	-0.5541	-0.5709	-0.5772	-0.5778	-0.5783

Table 4: Calculated dipole moments of optimized tautomers of 6-oxopurine (Deby)

Tautomer	Gas(1.0)	Benzene(2.2)	THF(7.6)	Methanol(33)	Water(78.4)
OP1	4.9492	5.7059	6.2351	6.44	6.4768
OP2	1.7378	2.0581	2.2887	2.3795	2.3958
OP3	10.439	12.209	13.4627	13.9507	14.0383
OP4	4.5897	5.336	5.86	6.0652	6.1021
OP5	4.4289	5.1044	5.5774	5.7607	5.7935
OP6	2.3234	2.727	3.0128	3.124	3.1439
OP7	5.0271	5.8317	6.3951	6.6133	6.6524

 

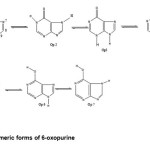Figure 1: Tautomeric forms of 6-oxopurine. Click here to View figure

References

1.  Grochowski, J., Serda, P., Markiewicz, M., Kozik, B., Sepiol, J.J., 2004. J. Mol. Struct. 689, 43.
2. Belova, N.V., Oberhammer, H., Girichev, G.V., Shlykov, S.A., 2008. J. Phys. Chem. A. 112, 3209.
3. Misra, A., Dalai, S., 2007. THEOCHEM 807, 33.
4. Zborowski, K., Korenova, A., 2004. THEOCHEM 683, 15.
5. Oziminski, W.P., Dobrovolski, J.C., Mazurek, A.P., 2004. THEO- CHEM 680, 107.
6. Dines, T.J., Onoh, H., 2006. Spectrochim. Acta A. 64, 891.
7. Shukla, M.K., Mishra, S.K., 2000. Comput. J. Chem. 21, 826.
8. Bonacin, J.A., Melo, D., Toma, H.E., 2007. Vib. Spectrosc. 44, 133.
9. Ralhan, S., Ray, N.K., 2003. THEOCHEM 634, 83.
10. Tavakol, H., 2010. THEOCHEM 956, 97.
11. M. Hyslop, I. Jardine, J. Pharmacol. Exp. Ther. (1981) 218.
12. R. Brockman, Cancer Res. 23 (1963) 1191.
13. Hurst, D. T. An Introduction to the Chemistry and Biochemistry of Pyrimidines, Purines and
14. Pteridines; John Wiley, New York, 1980, 179–203.
15. Rundless, R. W.; Wyngaarden, J. B.; Hitchings, G. H.; Elion, G. B.; Silberman, H. P. Trans. Assoc. Amer. Phys. 1963, 76, 126.
16. Elion, G. B.; Callahan, S.; Hitchings, G. H.; Rundles, R. W.; Laszlo, J. Cancer Chemother. Rept. 1962, 16, 1971.
17. Scanlan, M. J.; Hillier, I. H. J. Amer. Chem. Soc. 1984, 106, 3837.
18. Lin, J.; Yu, C.; Peng, S.; Akiyama, I.; Li, K.; Kao-Lee, L.; LeBreton, P. R. J. Phys. Chem. 1980, 84,1006.
19. Sheina, G. C.; Stepanian, S. G.; Radchenko, E. D.; Blagoi, Y. P. J. Mol. Struct. (Theochem.) 1987,158, 275.
20. Benoit, R. L.; Frechette, M. Can. J. Chem. 1985, 63, 3053.
21. Medeiros, G. C.; Thomas, G. J. J. Biochim. Biophys. Acta 1971, 238.
22. Lichtenberg, D.; Bergmann, F.; Neiman, Z. Isr. J. Chem. 1972, 10, 805.
23. Psoda, A.: Shugar, D. Biochim. Biophys. Acta 1971, 247, 507.
24. Chenon, M. T.; Pugmire, R. J.; Grant, D. M.; Panzica, R. P.; Townsend, L. B. J. Amer. Chem. Soc. 1975, 97, 4636.
25. Schmalle, H. W.; Hanggi, G.; Dubler, E. Acta. Crystallogr. 1988, C44, 732.
26. Dubler, E.; Hanggi, G.; Schmalle, H. W. Inorg. Chem. 1990, 29,
27. Izatt, R. M.; Christensen, J. J.; Ryttine, J. H. Chem. Rev. 1971, 71, 439.
28. Tauler, R.; Cid, J. F.; Casassas, E. J. Inorg. Biochem. 1990, 39, 277.
29. Pullman, B.; Pullman, A. Advan. Heterocyclic Chem. 1971, 13, 77.
30. Hernandez, B.; Luque, F. J.; Orozco, M. J. Org. Chem. 1996, 61, 5964.
31. Kassimi, N. El-B.; Thakkar, A. J. J. Mol. Struct. (Theochem.) 1996, 366, 185.
32. Nonella, M.; Hanggi, G.; Dubler, E. J. Mol. Struct. (Theochem.) 1993, 279, 173.
33. Contreras, J. G.; Alderere, J. B. Mole. Eng. 1992, 2, 29.
34. Miertus S, Scrocco E and Tomasi J, J Chem Phys., 1981, 55, 117.
35. Cances M T, Mennucci V and Tomasi J, J Chem Phys., 1997, 107, 3032-3037.
36. Cossi M, Barone V, Mennucci B and Tomasi J, Chem Phys Lett., 1998, 286, 253-260.
37. Barone V, Cossi M and Tomasi J, J Comp Chem., 1998, 19, 404-417.
38. Reed A E, Curtiss L A and Wienhold F, Chem Rev., 1988, 88, 899-926.
39. Najafi Chermahini A, Nasr-Esfahani M, Dalirnasab Z, Abdol Dabbagh H and Teimouri A, J Mol Struct., (Theochem)., 2007, 820, 7.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.