Theoretical Study of the Hydrogenation Reactions between 1,2-diazene and Flavonoid Molecules

Introduction

Flavonoids are a natural compounds of the polyphenols family present in substantial amounts in plants, fruits and vegetables consumed daily by humans [1-4]. Most of these compounds show an interesting biological activities such as radical scavenging and antioxidant [5-10]. The structure of flavonoids is given in Fig 1. This structure is also called the flavone 1a. The flavone 1a with OH groupe in position C3 is called flavonol 1b. The reduction double bond C2=C3 of flavone 1a and flavonol 1b give respectively flavanone 3a and flavanonole 3b molecules.

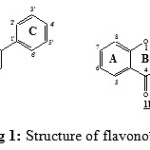Figure 1: Structure of flavonoïds Click here to View figure

 

In order to explain the existence  of flavanol 3a and flavanone 3b molecules obtained respectively by simple reduction double bond C2=C3 of flavone 1a and flavonol 1b molecules [11,12]. We found interesting to study from thermodynamic point of view the possibility and the stereoselectivity of  hydrogenation reactions between flavonoids molecules  1a-b and (Z) 1,2-diazene 2 and reactions between flavonoids 1a-b and  (E)-1,2-diazene 2′ (see Fig 2). In each case of these reactions we determine the corresponding transition states.

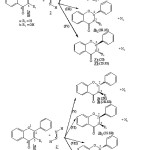Figure 2   Click here to View figure

 

Calculation methods

This study was carried using the GAUSSIAN 03 program [13]. The calculations were performed at SCF and DFT with the standard basis 6-311G*. We used the B3LYP functional in which the exchange energy is calculated by Becke’s three parameters method and the correlation method of Lee, Yang and Parr [14-16]. The choice of the DFT method is justified by its efficiency in the treatment of this systems type [17]. Computations of harmonic vibrational frequencies have been executed to verify the nature of the corresponding stationary points. The stationary points are classified as minima in the case, when no imaginary frequencies are found, and as a transition state if only one imaginary frequency is obtained [18]. In order to ensure that the transition states connect products, the intrinsic reaction coordinate (IRC) method [19] at the SCF/6-311G* and at B3LYP/6-311G* level of theory have been applied to each transition state of every reaction. Zero-point energies (ZPE) have been computed at the SCF/6-311G* and at the B3LYP/6-311G* level of theory, and the thermal corrections of each species has been added at 298,15K.

Results and discussion

Thermodynamic study

We study from thermodynamic point of view the possibility and the stereoselectivity of reactions between flavonoïds molecules type 1a-b and (Z)-1,2-diazene 2 and the reaction between flavonoïds type 1a-b and (E)-1,2-diazene 2′ (Fig 2). We determine under standard conditions of temperature and pressure (298.15 K and 1atm; 1atm = 100.325 kPa) the values of the different thermodynamic reaction state functions, such as energy ΔEr, free energy ΔGr, enthalpy ΔHr and ZPE corresponding to reactions (I) (II) (III) (IV) (V) (VI) (VII) and (VIII).

As shown in Table 1, values of free energy reaction ΔGr are all negative, so reactions are thermodynamically possible. We notice that the values of free energy reaction ΔGr corresponding to reactions (I) (II) (III) and (IV) are respectively higher (in absolute values of free energy reaction ΔGr) which corresponds to the reactions (V) (VI) (VII) and (VIII). This allow us to say that reactions (I) (II) (III) and (IV) are respectively more stable from thermodynamic point of view than the reactions (V) (VI) (VII) and (VIII). Moreover, the reactions (I) always give the major product of the reaction between molecules type 1a-b and (Z)-1,2-diazene 2. We also notice that the values of energy ΔEr corresponding to reactions (I) are higher (in absolute values of energy reaction) which corresponds to reactions (II) (III ) and (IV). This confirms again that the major products of the reactions are the stereoisomeres type 3a-b given by reaction (I).

We also notice that the values of free energy reaction ΔGr corresponding to the reaction between flavonol 1b and (Z)-1,2-diazene 2 are higher (in absolute values of free energy reaction) than the reaction between the flavone 1a and (Z) -1,2-diazene 2. This allow us to say that the reaction between flavonol 1b and (Z)-1,2-diazene 2 is more stable from thermodynamic point of view than the reaction between flavone 1a and (Z) -1,2-diazene 2.

Table 1 : Thermodynamic results of ΔEr,  ΔGr, ΔHr and  ZPE for  reactions (I-VIII)  (kcal.mol^-1).

Reactions	produits	ΔEr+ZPE	ΔHr	ΔGr
		B3LYP/ 6-311G*
Réaction (I)	3a3b	-79,39-85,15	-79,28-85,25	-77,12-83,19
Réaction (II )	3b1	-81,24	-81,34	-78,86
Réaction (III )	3b2	-80,02	-80,13	-77,03
Réaction (IV )	3’a3’b	-77,31-83,83	-77,21-83,93	-75,31-81,75
Réaction (V)	3a3b	-73,15-78,30	-73,25-78,41	-71,36-76,40
Réaction (VI )	3b1	-74,95	-74,85	-72,91
Réaction (VII )	3b2	-72,83	-72,93	-70,84
Réaction(VIII )	3’a3’b	-69,87-80,21	-69,98-80,10	-68,19-78,97
		SCF/ 6-311G*
Réaction (I)	3a3b	-78,54-83,69	-78,64-83,70	-76,88-82,06
Réaction (II )	3b1	-79,28	-79,18	-77,30
Réaction (III )	3b2	-78,81	-78,91	-76,19
Réaction (IV )	3’a3’b	-75,87-81,92	-75,97-81,82	-74,35-80,23
Réaction (V)	3a3b	-71,83-76,88	-71,82-76,87	-70,07-75,24
Réaction (VI )	3b1	-74,22	-74,21	-72,04
Réaction (VII )	3b2	-73,01	-73,11	-70,16
Réaction(VIII )	3’a3’b	-69,77-80,12	-69,87-80,02	-67,95-78,41

 

Transition states

The thermodynamic study shows that hydrogenation reactions between molecules type 1a-b and (Z)-1,2-diazene 2 are more stable than the reactions between molecules 1a-b and  (E)-1,2-diazene 2 ‘. We then continue our transition state study on the reactions between flavonoids  1a-b and (Z)-1,2-diazene 2.

First, we determine the transition state of reaction between (Z)-1,2-diazene and flavone 1a in both approaches endo and exo. As shown in Fig 3, the endo form 3’a*_(endo) gives the product 3’a (2S) and the exo form 3a*_(exo) gives the stereoisomer 3a (2R). Table 2 shows that the activation energy corresponding to exo form 3a*_(exo) is higher than the activation energy corresponding to endo form 3’a*_(endo). This implies that the endo form is more favorable than the exo form. Furthermore, the stereoisomer 3’a is the kinetic product and the stereisomer 3a is the thermodynamic product of reaction between (Z)-1,2-diazene 2 and flavone 1a (Fig 4). This confirms the existence of flavanone 3a(2R). However the existence of compound 3’a(2S) is not possible in nature [1-4].

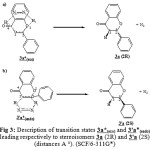Figure 3: Description of transition states 3a*(exo) and 3’a*(endo) leading respectively to stereoisomers  3a (2R) and 3’a (2S) (distances A °). (SCF/6-311G*) Click here to View figure

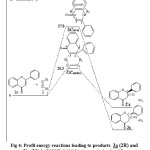Figure 4: Profil energy reactions leading to products  3a (2R) and  3’a (2S) in B3LYP/6-311G* (energy in kcal.mol-1).   Click here to View figure

 

Table 2: E*(kcal.mol^-1) energies of transition states relative to reactants energies (B3LYP/ 6-311G* and SCF/6-311G*).

	(B3LYP /6-311G*)	( SCF/ 6-311G*)
21a 3a*(exo) 3’a*(endo) 1b 3b*(exo) 3b1*(endo) 3b2*(exo) 3’b*(endo)	27.8 26.3   29.7 29.2 30.2 28.1	28.1 26.7   30.2 29.8 31.7 28.9

 

Second, we determine the transition states of reaction between (Z)-1,2-diazene 2 and flavonol 1b in both approaches endo and exo. As shown in fig 5, we find transition states of compounds 3b₂*_(exo), 3b*_(exo), 3b₁*_(endo) and 3’b*_(endo) leading respectively to stereisomers 3b₂(2R 3S), 3b(2R 3R), 3b₁(2S 3R) and 3’b(2S 3S). The corresponding Activation energies are reported in table 2. The results show that the activation energy corresponds to endo forms 3’b*_(endo) and 3b₁*_(endo) are less than the activation energy corresponding to exo forms 3b*_(exo) and 3b₂*_(exo). Moreover, the activation energy corresponding to endo form 3’b*_(endo) is less than endo form 3b₁*_(endo). Therefore the compound 3’b(2S 3S) is the kinetic product but 3b(2R 3R) is the thermodynamic product of the reaction between flavonol 1b and  (Z)-1,2-diazene 2.

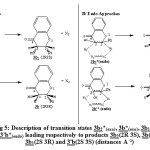Figure 5: Description of transition states 3b2*(exo), 3b*(exo), 3b1*(endo) and 3’b*(endo) leading respectively to products 3b2(2R 3S), 3b(2R 3R), 3b1(2S 3R) and 3’b(2S 3S) (distances A °). Click here to View figure

 

The comparison of energy profiles of reactions leading respectively to stereoisomers 3b₂(2R 3S), 3b(2R 3R), 3b₁(2S 3R) and 3’b(2S 3S) is given in Fig 6. We notice that the stereoisomer 3b (2R3R) is more stable from thermodynamic point of view than stereoisomers 3b₂(2R 3S),  3b₁(2S 3R) and 3’b(2S 3S). So we can say that the compound 3b (2R3R) is the thermodynamic product and compound 3’b(2S 3S) is the kinetic product of the reaction between flavonol 1b and (Z)-1,2-diazene 2.

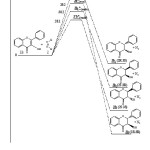Figure 6: Profile energy reactions leading to products 3b2(2R 3S), 3b(2R 3R), 3b1(2S 3R) and 3’b(2S 3S) in B3LYP/ 6-311G* (energy in kcal.mol-1). Click here to View figure

 

Our theoretical results clearly confirm the existence of stereoisomere 3b that is thermodynamically more stable than stereoisomeres 3’b(2S 3S), 3b₁(2S 3R) and 3b₂(2R3S). This explains well the existence of flavanone 3b in different plants [1-4].

In the end, we compare the formation bond lengths in the transition state of reaction between flavonoids 1a-b and (Z)-1,2-diazene 2 (Fig 3 and Fig 5). We find that the bond C₂H₁ is shorter than the bond C₃H₂ (Table 3). These distances are quite similar to that found by McKee et al for the reaction between (Z)-1,2-diazene 2 and ethene [20].

Table 3: Bond lengths of C₂H₁ and C₃H₂ formed in the transition state of reaction between (Z) -1,2-diazen  2 and flavonoids type 1a-b.

	B3LYP/6-311G*		SCF/6-311G*
	C2H1	C3H2	C2H1	C3H2
3a* (exo)3’a*(endo) 3b*(exo) 3b1*(endo) 3b2*(exo) 3’b*(endo)	1.5691.569 1.570 1.569 1.571 1.569	1.5711.572 1.571 1.571 1.572 1.571	1.5721.571 1.571 1.572 1.571 1.571	1.5741.575 1.574 1.574 1.573 1.573

 

Conclusion 

In this work, we study the possibility and the stereoselectivity of the hydrogenation reactions between flavonoïds 1a-b and (Z)-1,2-diazene 2 and reaction between flavonoïds 1a-b and (E)-1,2-diazene 2′. Our theoretical results show that these reactions are possible from thermodynamic point of view. Further reactions between (Z)-1,2-diazene 2 and flavonoids type 1a-b are more stable from thermodynamic point of view than the reactions between (E)-1,2-diazene 2′ and flavonoids  1a-b. The results also show that stereoisomere 3a(2R) is more stable from thermodynamic point of view than stereoisomere 3’a(2S). Although the activation energy corresponding to endo form 3’a*(endo) is less than the activation energy corresponding to exo form 3a*(exo). This implies that 3’a (2S) is the kinetic product and flavanone 3a (2R) is the thermodynamic product of the reaction between flavone 1a and (Z)-1,2-diazene 2.

In the case of reaction between flavonol 1b and (Z)-1,2-diazene 2, results show that flavanonole 3b (2R3R) is more stable from thermodynamic point of view than products 3b’(2S3R), 3b₁(2S3R) and 3b₂(2R3S). However, the transition state calculations show that the endo forms 3’b*(endo) and 3b₁*(endo) are more stable than the exo forms 3b*(exo) and 3b₂*(exo). Furthmore, the activation energy corresponding to 3’b*(endo) is less than the activation energy corresponding to 3b*(exo). This implies that 3’b(2S3R) is the kinetic product and 3b(2R3R) is the thermodynamic product of the reaction between flavanol 1b and (Z)-1,2-diazene 2.

References

1. Mullen.W, Marks.S.C, Crozier.A, Journal of Agricultural and Food chemistry, 2007, 55, 3148.
2. Stratil.p, Klejdus.B, Kuban.V, Journal of agricultural and Food chemistry, 2006, 54, 607.
3. Rocio Garcia-villalba, Alegria carrasco-pancorbo, cristinaoliveras-Ferraros, Alejandro Vazquez-Martin, Javier.A.Menendez, Antonio Segura-carretero, Alberto Fermandez, Journal of pharmaceutical and biomedical analysis, 2010, 51, 416.
4. G.Kouakou-siransy, S.Sahpez, G.Irié-Nguessan, Y.J.Datte, J.Kablan, B.Gressier, F.Bailleul, Food Chemistry, 2010, 118, 430.
5. Jessica Tabart, Claire Kevers, Joël Pincemail, Jean-olivier Defraigne, Jacques Dommes, Food Chemistry, 2010, 120, 607.
6. Arts.I.C, Hollman.P.C, American Journal of clinical nutrition, 2005, 81,317s.
7. Bravo.L, Nutrition reviews, 1998, 56, 317.
8. Tabart.J, Kevers.C, Pincemail.J, Defraigne.J.O, Dommes.J, Food Chemistry, 2009, 113, 1226.
9. villano.D, Fermandez-pachon.M.S, Troncoso.A.M, Garcia-parrilla.M.C, Analytica Chimica Acta, 2005, 538, 391.
10. oxygenolysis of flavonoid compounds. DFT description of the mechanism for the quercetin case. Chemphys Chem 2004, 5, 1726.
11. Harborne J.B et Mabry T.J: The flavonoïds: advances in research; edition hardback; 1982, 3, 38.
12. Moyse H. et parisR.R, Précis de matière medicinal, Tome II; edition par Masson; 1967, 129, 301 and  370-375.
13. Gaussian 03, Revision A. 1, M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Peterson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T.Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chem, M. W. Wong, C. Gonzalez, and J. A. Pople, Gaussian, Inc., Pittsburgh PA, 2003.
14. C. Lee, W. Yang,  R. G. Parr, Phys. Rev. B,1988,  37, 785.
15. A. D. Becke,  Phys.  Rev. A., 1988, 38, 3098.
16. A. D. Becke, J. Chem. Phys, 1993, 98, 5648.
17. E. Goldstein, Brett Beno, K.N. Houk, J.Am.Chem.Soc, 1996, 118, 6036.
18. H. B. Schlegel, J. Comput. Chem, 1982, 2, 214.
19. a/ C. Gonzalez, H. B. Schlegel, J Chem Phys, 1989, 90, 2154. b/ C. Gonzalez, H. B. Schlegel, J Chem Phys, 1990, 94, 5523.
20. Mc Kee.M.L, M.E.Squillacote, D.M.Stanbury, J.Phys.Chem, 1992, 96, 3266.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.