Vibrational Spectra of Ozone (O3) Using Lie Algebraic Method
Department of Mathematics, School of Technology, GITAM, Hyderabad, India
Corresponding Author E-mail: vijayjaliparthi@gmail.com
DOI : http://dx.doi.org/10.13005/ojc/3404065
Article Received on : 01-04-2018
Article Accepted on : 19-05-2018
Article Published : 02 Aug 2018
We have calculated the vibrational frequencies of Ozone (O3) upto second overtone using Hamiltonian operator which is based on the Lie algebra. The determined symmetric and antisymmetric fundamental vibrational frequencies by Lie algebraic method are compared with experimental data. It has been observed that results from the method reveal near to the exact, consistent with the experimental data.
KEYWORDS:Lie algebraic method; Ozone; Vibrational spectra
Download this article as:| Copy the following to cite this article: Vijayasekhar J. Vibrational Spectra of Ozone (O3) Using Lie Algebraic Method. Orient J Chem 2018;34(4). |
| Copy the following to cite this URL: Vijayasekhar J. Vibrational Spectra of Ozone (O3) Using Lie Algebraic Method. Orient J Chem 2018;34(4). Available from: http://www.orientjchem.org/?p=47985 |
Introduction
In 1981, Iachello presented Lie algebraic framework to molecular spectra of small molecules.1,2 This framework based on Schrodinger equation with a Morse potential function and described ro-vibration spectra of diatomic molecules.3,4 Later this method was extended to calculate medium and large molecules.5-16 Apart from this framework, there are two other well-known methods established to calculate vibrational spectra of molecules. The first one is Dunham expansion.17 In this expansion the energy levels are expanded in ro-vibrational quantum numbers. In the second approach interatomic potential can be expanded interms of interatomic variables and potential coefficients by solving Schrodinger equation. The coefficients are fitted with an available experimental data. The major drawback in both the methods is large experimental data is required to fit parameters, which is not possible eveytime. In order to this major difficulty we consider the third approach Lie algebraic method.
Lie Algebraic Method for the Triatomic Molecule Ozone
Ozone (O3) contains three oxygen (O) atoms. The Ozone consists of two O-O bonds. The symmetry point group is C2v.
 |
Figure 1: Structure of Ozone. |
The Hamiltonian [18] in the case of stretching vibrations for Ozone (O3) is H as follows
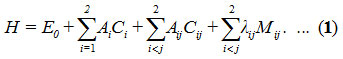
In Hamiltonian, Ci and Cij are invariant operators of uncoupled and coupled bonds respectively and given by
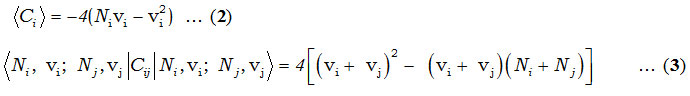
and the Majorana operator, Mij is used to describe local mode interactions in pairs. This contains diagonal and non-diagonal matrix elements,
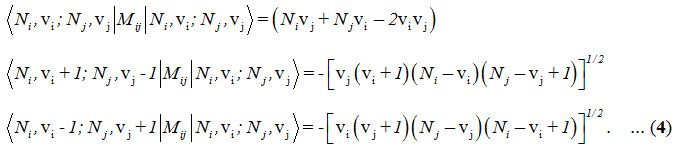
Here i vary from 1 to 2 for two stretching bonds (O-O and O-O).
Eq. (1) can be written as
![]()
where A1, A2, A12 and λ12 are parameters, which are determined by spectroscopic data. The parameters λij illustrate the interactions between stretching bonds ( λ12). The local stretching vibrations are denoted by V1 and V3, while V2 denotes bending vibrations for Ozone (O3). Since, two bonds (O-O) are equivalent, place A1 = A2 = A, N1 = N2 = N in equations (2), (3) and (4). All parameters are in cm-1, except N, which is dimension less. Eigen values of the Hamiltonian matrix will be considered as vibrational frequencies of Ozone.
Hamiltonian matrix for the first two local modes is given by
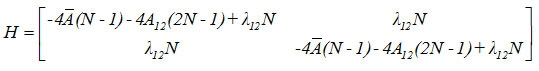
Results and Discussion
First calculate the Vibron number for stretching bonds of Ozone usin
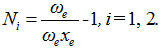
In this equation, ωe, ωe xe are harmonic vibrational frequency and vibrational anharmonicity (spectroscopic) constants respectively. For the stretching mode, the values of ωe and ωe xe for the O-O bond are 1580.161 and 11.95127 respectively.19
The initial value for the parameter A is obtained by using the energy.20,21
![]()
Hence, ‾A can be evaluated as,
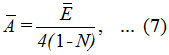
where ¯E is the average of two different energies, related to symmetric (E1) and antisymmetric (E2) combinations of local modes.
To find an initial value for λ12 whose role is to split the initially degenerate local modes is calculated by the relation,11
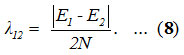
A mathematical fitting procedure is used to adjust the parameter A12 and calculated as 0.028. Calculated vibrational frequencies of Ozone by the Lie algebraic method are reported in the table (1).
Table 1: The experimental and calculated vibrational frequencies (in cm-1) of Ozone.
|
Symmetry species |
Experimental [http://vpl.astro.washington.edu/spectra/o3.htm] |
Calculated |
|
|
(1 0 0) |
A1 (Symmetric) |
1103 |
1103.7920 |
|
(0 0 1 ) |
B1(Antisymmetric) |
1042 |
1043.0080 |
|
(2 0 0) |
– |
– |
2206.0020 |
|
(0 0 2) |
– |
– |
2061.0671 |
|
(1 0 1) |
– |
– |
2109.2761 |
|
(3 0 0) |
– |
– |
3289.0042 |
|
(0 0 3) |
– |
– |
3046.9751 |
|
(2 0 1) |
– |
– |
3187.0953 |
|
(1 0 2) |
– |
– |
3085.9872 |
![]()
Conclusion
In the table (1), vibrational frequencies of Ozone (O3) upto second overtone by Lie algebraic method are reported and also symmetric and antisymmetric fundamental vibrational frequencies compared with available experimental data. For the fundamental vibrational frequencies we observed that the root mean square deviation is 0.3542. The obtained results are useful for the experimentalists and theorists to develop the vibrational frequencies of Ozone in higher overtones.
References
- Iachello, F., Interacting Bose-Fermi systems in nuclei, (Plenum, New York, 1981).
CrossRef - Iachello, F., Interacting Bosons in nuclear physics, (Plenum, New York, 1979).
CrossRef - Iachello, F., Chem. Phys. Lett. 1981, 78, 581-585.
CrossRef - Iachello, F.; Levine, R. D., J. Chem. Phys. 1982, 77, 3046-3055.
CrossRef - Karumuri, S. R.; Sravani, K. G.; Sekhar, J. V.; Reddy, L. S. S. Acta Phys. Pol. A. 2012, 122(1), 1111-1114.
- Rao, K. S.; Srinivas, G.; Sekhar, J. V.; Rao, V. U. M.; Srinivas, Y.; Babu, K. S.; Kumar, V. S. S.; Hanumaiah, A. Chin. Phys. B. 2013, 22(9), 090304 (1-8).
- Rao, K. S.; Sekhar, J. V.; Sreeram, V.; Rao, V. U. M.; Rao, M. V. B. J. Mol. Spectrosc. 2011, 269, 119-123.
CrossRef - Sekhar, J. V.; Rao, K. S.; Prasad, B. V. S. N. Orient. J. Chem. 2016, 32(3), 1717-1719.
CrossRef - Van Roosmalen, O. S.; Dieperink, A.E.L.; Iachello, F. Chem. Phys. Lett. 1982, 85, 32-36.
CrossRef - Van Roosmalen, O. S.; Iachello, F.; Levine, R.D.; Dieperink, A.E.L. J. Chem. Phys. 1983, 79, 2515-2536.
CrossRef - Van Roosmalen, O. S.; Benjamin, I.; Levine, R.D. J. Chem. Phys. 1984, 81, 5986-5997.
CrossRef - Iachello, F.; Oss, S. Phys. Rev. Lett. 1991, 66, 2976-2979.
CrossRef - Iachello, F.; Oss, S. J. Chem. Phys. 1996, 104, 6956-6963.
CrossRef - Frank, A.; Van Isacker, P. Algebraic methods in molecular and nuclear structure physics, (Wiley, New York, 1994).
- Iachello, F.; Levine, R. D. Algebraic theory of molecules, (Oxford University Press, Oxford, 1995).
- Iachello, F.; Oss, S. Eur. Phys. J. D. 2002, 19, 307-314.
- Dunham, J. L., Phys. Rev. 1932, 41, 721-731.
CrossRef - Karumuri, S.R.; Rao, V. U. M.; Sekhar, J. V.; Babu, M. S. S.; Patrudu, T. B.; Krishna, N. V.; Babu, K. S.; Kumar, V. S. S.; Srinivas, G. Ukr. J. Phys. 2013, 58(9), 836-840.
CrossRef - Karl K. Irikura, J. Phys. Chem. Ref. Data. 2007, 36(2), 389-397.
CrossRef - Oss, S., Adv. Chem. Phys. 1996, 93, 455-649.
- Iachello, F.; Oss, S. J. Mol. Spectrosc. 1992, 153, 225-239.
CrossRef

This work is licensed under a Creative Commons Attribution 4.0 International License.










