Thermoanalytical and Kinetic Studies for the Thermal Stability of Nimesulide under Different Heating Rates

Introduction

Nimesulide (4-nitro-2-phenoxymethanesulfonanilide) has a nitroaromatic ring and is extensively used as a nonsteroidal anti-inflammatory (NSAID) medication that specifically inhibits prostaglandin formation¹. Furthermore, nimesulide contains antipyretic and analgesic characteristics that may be used to treat rheumatoid arthritis, prostatovesiculitis, and osteoarthritis ².

Thermal analysis is a common quality control tool for pharmaceutical medications and chemicals that offers important facts regarding the physical characteristics of materials ^{3, 4}

Thermogravimetric analysis (TG) is frequently the gateway in the comprehensive exploration for a specific drug’s characteristic and for determining its compatibility in single form or in the presence of other constituents, thermal stability, and kinetic examination. Additionally, with minimal amounts of material and without the use of solvents, results may be reached rapidly. ⁵. The thermogravimetry data collected by thermal decomposition may be evaluated to derive kinetic parameters. The use of thermoanalytical methods may yield fresh insights into the temperature and energy involved with phenomena like melting, glass transition, oxidation reactions, decomposition, crystallisation, or crystal transition ⁶.

The thermal degradation of pharmaceuticals is significant because it may be used to anticipate degradation (decomposition) rates at lower values of heating using data from accelerated routes investigated at high temperatures. The temperature might raise the temperature of chemical processes, supplying enough activation energy to disruption the chemical links and start the degradation pathway. Understanding of such variables are useful for elucidating incompatibility and the influence on the stability in both pure pharmaceuticals and drug–excipient combinations.

Nimesulide is determined using different techniques including liquid chromatography^7-9, spectrophotometry^10-12, and electrochemical methods ^13-17.

The purpose of this research is to look at the thermal behaviour and kinetics of nimesulide decomposition using non-isothermal settings at changed heating rates. Moreover, to the best of our knowledge, no information regarding the nimesulide’s thermal characteristics or degradation kinetics.

Experimental

Materials

Nimesulide was offered from Pharaonia Co., Alex, Egypt, and the purity is 99.36%.

Apparatus

Simultaneous Shimadzu Thermogravimetric Analyzer TGA-60 H with TA 60 software was used to perform thermogravimetry and differential thermal analysis in a platinum crucible in a dry nitrogen environment via a flow rate of 30 mL min^-1. The studies were carried out at various heating speeds from room temperature to 800 ^oC. (5, 10, 15 and 20 ^oC min^-1). Without any additional treatment, the drug mass was around 5 mg of the nimesulide. TG/DTG curves were used to derive decomposition kinetic parameters.

Results and discussion

Thermal behavior of nimesulide

The thermoanalytic graphs that define the thermal demeanor of nimesulide in raised temperature setting with a rate of heating of 5 °C/min under N₂ gas environment are displayed in Figure1. By depicting the TG/DTG plots, two distinct steps with different mass loss are presented. The first stage corresponds to the loss of -C₁₂H₉N₂O₃ (Δm = 74.35%) and happens between 210 °C to 385 °C, with T_{peak DTG} = 305 °C.

Figure 1: Thermogravimetric analysis, TG/DTG with DTA graphs of nimesulide under dynamic N2 gas atmosphere (30 mL min-1) using heating rate at 5 oC/min. Click here to View figure

In the temperature range 386–680 ^oC, the second disintegration phase shows a mass loss (m = 25.65%), indicating full nimesulide decomposition.

The DTA plot represents a significant thermal occurrence across the studied range of temperature.

The endothermic event at 145 ^oC ¹⁸ is most probable owing to nimesulide melting, whereas the exothermic event at 320 ^oC is described to the first breakdown course linked with the 1^st mass loss shown in the TG/DTG curve as shown in Figure 2. A significant exothermic peak is detected at 610 ^oC due to the complete pyrolysis of nimesulide. The proposed nimesulide thermal breakdown is best exemplified in Scheme 1.

Scheme 1: The suggested thermal degradation of nimesulide Click here to View scheme

Effect of heating rate

Figure 2 depicts nimesulide weight-loss curves at various heating speeds ranging from 5 to 20 °C/min. When shown in the graph, as the heating rate rises, the T_max values move to higher values. Furthermore, the curves show that nimesulide breakdown occurs in a two phase, with no evolution of water contents at the start of the process.

Figure 2: Thermograms of nimesulide in nitrogen atmosphere at different heating rates. Click here to View figure

DTA data for the decomposition of nimesulide at various rates of heating is depicted in Figure 3. The melting point events and disintegration temperatures of the medications were found to be moved to upper temperatures by increasing the heating rate.

Figure 3: DTA curves of nimesulide at different heating rates. Click here to View figure

Kinetic models

The kinetic factors found from the current studies done using non-isothermal circumstances were utilized to evaluate the nimesulide thermal stability. The following kinetic models were used to determine the moving strictures using the TG/DTG graphs: Friedman (Fd) ^{19, 20}, Flynn–Wall–Ozawa (FWO) ^21-23, and Starink (St)²⁴ .

Usually, the kinetics of processes (such as polymerization, crystallisation, decomposition, etc) may be delineated using rate equations ^{25, 26}:

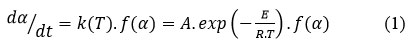
where t is referring to the time, k(T) is referring to the Arrhenius rate constant, α is referring to the degree of conversion, A is referring to the pre-exponential factor  and E is defining the activation energy, R is referring to the universal gas constant, and f (α) is defining the reaction model related to a the persuaded decomposing pathway. Utilizing non-isothermal settings, the term dα/dt is converted with βdα/dT, where β is referring to the rate of heating, yielding.

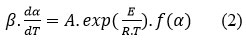
Friedman (Fd) method

The isoconversional Friedman technique is dependent on the generic reaction rate relation ³

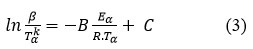
where B and C are constants. The rate equation is transformed into:

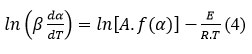
The graphical depiction of da / dt versus 1/T for = const. and varying heating rates (β) give rise to straight lines, their slope is defined E. A sequence of straight lines, known as the Friedman diagram, is obtained for various values of (Fig. 3).

Flynn–Wall–Ozawa (F–W–O) approach

Flynn–Wall–Ozawa is considered as one of the integral isoconversional approaches that uses the integral relation of the rate as well as the Doyle approximation for p (x):

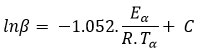
For α= const., plotting lnβ according to 1/T yields a straight line relation and the energy of activation (E) could be obtained from the slope. A straight family is obtained for various values of (Figure 4). When the heating rate is increased, there is a variation in the mechanism or the rate-determining step. Table 1 shows the activation energy (E) values.

Figure 4: Plot of Friedman’s for nimesulide at variant heating rates (A), The Flynn–Wall–Ozawa (B), and Starink (C) plots Click here to View figure

Starink (St) method

St proposes the following estimation for the integral temperature:

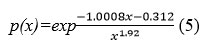
The values of E were estimated using the Starink technique from the slope of the fitted relation of ln/

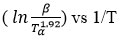
(Figure 4C) and are presented in Table 1.

Table 1: nimesulide calculated activation energy values using Friedman (Fd), Flynn–Wall–Ozawa (FWO), and Starink (ST) approaches

Technique		E/kJ mol-1, for conversion degree, α
	0.05		0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9
FR	133.0		138.1	137.1	138.8	137.1	139.6	137.5	139.1	139.2	133.2
FW	129.6		129.94	130.19	130.61	130.61	130.77	130.94	131.07	131.19	129.69
Starink	131.6		130.7	130.9	131.1	130.6	131.3	132.1	132.1	132.2	131.6

The obtained observations have been made based on the collected results include that the activation energies determined via the Fd approach, FWO, and Starink techniques are quite similar throughout the whole decomposition fraction range. These findings are consistent with the published data on the accuracy offered by these approaches. The activation energy (E) values obtained by these approaches are in worthy convention, and the low fluctuation of E vs. designates a unistadial, yet complicated decomposition pathway. Given that 65% of the E vs. α amount identified in the literature are in the 100 to 230 kJ mol^-1 range, the E values revealed a significant thermal stability of the nimesulide -active chemical ²⁷.

Conclusion

Nimesulide was exposed to a thermal examination in an inert nitrogen environment under non-isothermal circumstances. The thermal stability of nimesulide was investigated in this work utilising thermal techniques and kinetic analysis. Its thermal behaviour was monitored for this purpose, and a kinetic analysis was carried out to estimate the activation energy. The way nimesulide reacts to heat demonstrates a high degree of thermal stability (up to 210 °C). Differential techniques (Fd technique) and integral approaches were utilized to calculate the kinetic parameter values. According to the findings, nimesulide decomposition happens in two steps. The values of thermodynamic functions calculated using differential and integral approaches were found to be in good agreement. This demonstrates the precision of the techniques used. The computed activation energy might be particularly valuable throughout the drug quality control and preformulation stages of manufacture.

Acknowledgement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Conflicts of interest

The authors declare no conflict of interest.

Funding Sources

There is no funding sources.

References

1. Davis R.; Brogden R. N., Drugs1994, 48, 431-54.
   CrossRef
2.  Haraoui B.; Pelletier J. P.; Cloutier J. M.; Faure M. P.; Martel‐Pelletier J., Arthritis & Rheumatism: Official Journal of the American College of Rheumatology 1991, 34, 153-63.
   CrossRef
3. Mohamed M. A.; Attia A. K., Journal of Thermal Analysis and Calorimetry 2017, 127, 1751-6.
   CrossRef
4. Mohamed M. A.; Atty S. A.; Banks C. E.; Journal of Thermal Analysis and Calorimetry 2017, 130, 2359-67.
   CrossRef
5. Fandaruff C.; Araya-Sibaja A.; Pereira R.; Hoffmeister C.; Rocha H.; Silva M., Journal of Thermal Analysis and Calorimetry 2014, 115, 2351-6.
   CrossRef
6. Salama N. N.; Mohammad M. A.; Fattah T. A., Journal of Thermal Analysis and Calorimetry 2015, 120, 953-8.
   CrossRef
7. Chandran S.; Ravi P.; Jadhav P. R.; Saha R. N., Analytical Letters 2008, 41, 2437-51
   CrossRef
8. Khaksa G.; Udupa N., Journal of Chromatography B: Biomedical Sciences and Applications 1999, 727, 241-4.
   CrossRef
9. Patravale V. B.; D’Souza S.; Narkar Y., Journal of Pharmaceutical and Biomedical Analysis 2001, 25, 685-8.
   CrossRef
10. Altinöz S.; Dursun Ö. Ö., Journal of Pharmaceutical and Biomedical Analysis 2000, 22, 175-82.
    CrossRef
11. Chandran S.; Saggar S.; Priya K. P.; Saha R. N., Drug Development and Industrial Pharmacy2000, 26, 229-34.
    CrossRef
12. Upadhyay K.; Asthana A.; Tiwari N.; Mathew S. B., Research on Chemical Intermediates 2013, 39, 3553-63.
    CrossRef
13. Deroco P. B.; Rocha-Filho R. C.; Fatibello-Filho O., Talanta 2018, 179, 115-23.
    CrossRef
14. Łysoń M.; Górska A.; Paczosa-Bator B.; Piech R., Electrocatalysis 2021, 12, 641-9.
    CrossRef
15. Shetti N. P.; Malode S. J.; Bukkitgar S. D.; Bagihalli G. B.; Kulkarni R. M.; Pujari S. B. et al., Materials Science for Energy Technologies 2019, 2, 396-400.
    CrossRef
16. Wang C.; Shao X.; Liu Q.; Qu Q.; Yang G.; Hu X, Journal of Pharmaceutical and Biomedical Analysis 2006, 42, 237-44.
    CrossRef
17. Wong A; Santos A. M.; Fatibello-Filho O, Journal of Electroanalytical Chemistry 2017, 799, 547-55.
    CrossRef
18. Constantinescu I. C.; Florea M.; Arama C-C.; Nedelcu A.; Monciu C-M, Farmacia 2009, 57, 267-71.
19. Friedman H. L., Journal of Polymer Science Part C: Polymer Symposia; 1964: Wiley Online Library.
20. Friedman H. L., Journal of Polymer Science Part B: Polymer Letters 1969, 7, 41-6.
    CrossRef
21. Flynn J. H.; Wall L. A., J Res Nat Bur Stand 1966, 70, 487-523.
    CrossRef
22. Flynn J. H.; Wall L. A., Journal of Polymer Science Part B: Polymer Letters 1966, 4, 323-8.
    CrossRef
23. Ozawa T., Bulletin of the chemical society of Japan1965, 38, 1881-6.
    CrossRef
24. Starink M., Thermochimica Acta 2003, 404, 163-76.
    CrossRef
25. Brown M., Thermal Decomposition of Ionic Solids. Elsevier Science; 1999.
26.  Brown M. E.; Dollimore D.; Galwey A. K., Reactions in the solid state. Elsevier; 1980.
27. Galwey A. K., Thermochimica acta 1994, 242, 259-64.
    CrossRef

---

This work is licensed under a Creative Commons Attribution 4.0 International License.