Rheological Behavior of Ruminal Fluid Obtained from Barley Feed Sheep

Introduction

In general, fluids do not follow the mathematical model given by Newton’s law for flow, shown in Figure 1a:

where τ represents the shear stress, expressed in Pa, η – the dynamic viscosity, expressed in Pa · s and γ – shear rate, expressed in s^-1. These are non-Newtonian fluids, for which the viscosity is no longer constant, but changes with shear rate (at constant composition and temperature).

Non-Newtonian fluids have the following types of flow: ideal, pseudoplastic and dilating plastic, which can be highlighted by the flow curves, also called rheograms, τ = f(γ) ,shown in Figure 1.

Figure 1: Rheograms for: a – Newtonian flow; a ‘- ideal plastic; b – pseudoplastic with zero flow, b ‘- pseudoplastic with flow limit voltage; Click here to View figure

For the ideal plastic flow the rheogram is linear, as for the Newtonian one (figure 1a ‘), but the line meets the voltage axis at a certain value called limit or critical flow voltage, τ₀ (figure 1a ‘). Such fluids are also called Bingham bodies, the mathematical relation that quantitatively describes this behavior being given by the Bingham model:  

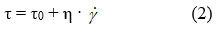
The flow limit stress – defined as the minimum stress that must be applied to a concentrated polymer solution to flow – is a very important parameter, causing the containers to flow due to their own weight when they are placed in the reverse or horizontal position.

The ideal plastic flow is found in thick greases and some oils that contain large amounts of dissolved polymers.

Pseudoplastic flow is characterized by the fact that the viscosity, called apparent, decreases with increasing shear rate (the solution becomes thinner). In this case, the rheogram does not show any linear portion, the viscosity of the solution being still constant (figure 1b, b ‘).

Pseudoplastic behavior can be explained by the existence of structures that are partially or completely destroyed during flow. Thus, the decrease in viscosity as the shear rate increases, respectively the shear stress, is due, in some cases, to the destruction of agglomerates formed by hydrogen bonds or van der Waals forces.

For dilating flow, the viscosity increases with increasing shear rate, as in Figure 1c, c ‘.

The following describes the mathematical models used to study pseudoplastic and dilating behavior.

The Ostwald-de Waele model, with the relation speed-tension of shear has the form:

where K is a constant called the consistency index or viscosity descriptor, and the exponent n is called the flow index or plasticity descriptor, describing the deviation of the flow from Newtonian behavior. Its value is between 0 and 1 for pseudoplastic fluids and greater than 1 for dilating fluids (n = 1 for Newtonian fluids). According to this model, the flow starts at zero shear stress. Apparent viscosities are determined from the tangent at each point in the rheogram.

Herschel-Bulkley model derived from the previous one, by completing a term τ0, to take into account the flow limit voltage:

The Ostwald-de Waele and Herschel-Bulkley models are also known as power law models and are used to describe the pseudoplastic behavior of concentrated solutions.

The Cross model describes the relationship between viscosity and shear rate as ^1-3:

where η₀ is the viscosity at the lowest shear rate, η_∞ – viscosity at the highest shear rate, β – constant expressed in units of time, and m – dimensionless quantity called shear index. The degree of thinning of the sample (pseudoplasticity) is given by the value m: when it approaches zero the system approaches the Newtonian behavior, and when it approaches 1, the system approaches the pseudoplastic behavior ⁴.

Rheological models describing the behavior of ruminal fluid in sheep obtained from oat feed. Model Carreau:

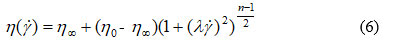
Where h₀ viscosity at zero shear rate (Pa.s), h_∞ viscosity at infinite shear rate (Pa.s), _λ relaxation time (s) and n power index ^{5-11, 10-17}.

Model Vocaldo:

Model Casson

where τ is the shear stress, τ_o – yield stress, η – viscosity, γ– shear rate, n – flow index and k – index of consistency.

Material and methods

The study of rheological behavior was done for ruminal fluid obtained from sheep feed with barley and feed with barley and yeast, fluid harvested after two diets: the classic diet (concentrated with 40% oats) and the classic diet with the addition of feed yeast ^7-9. Measurements were made at 39°C, with a Physica MCR 300 rheometer, using the DG26.7 concentric cylinder measuring system.

Results and discussion

From the experimental data it is found that the viscosity values decrease as the shear rate increases, it appears that the ruminal fluid has a pseudoplastic fluid behavior in both types of diet. The appearance of the rheograms in figure 1 confirms the pseudoplastic character of this fluid.

For the interpretation of the experimental data it was assumed that the experimental dependence τ = f(γ)  can be described by the model of the law of power (relation 1).

The expression of the law of power (relation 1) can be linearized by logarithm:

The graphical representation of this model, ṙṙṙfrom the intersection to the ordinate the value of ln K is obtained, and from the slope the value of n, as can be seen from figure 2. For the two types of fluids the results from table 1 were obtained. for K and n, the calculated values for the dependencies were obtained τ = f (γ) , respectively η_a = f(γ) .

Figure 2: The influence of shear rate on the experimental values of shear stress and apparent viscosity for ruminal fluid obtained from feed with barley 40%. Click here to View figure

Continuous line – calculated dependency τ = f (γ) , dotted line – calculated dependency η = f(γ).

Figure 3: Linearization of experimental dependence  for the two ruminal fluids. Click here to View figure

As can be seen from Figure 2, the calculated dependencies overlap very well over the experimental values, which confirms that the power law model can be used to interpret the rheological behavior of ruminal fluid.

Table 1: Rheological characteristics of ruminal fluids obtained by linear regression applied to the linearized form of experimental dependence τ = f (γ).

Rheological characteristics	The classic diet	The classic diet with the addition of feed yeast
n	0.483±0.008	0.436±0.013
K (mPa . s)	16.59±0.28	7.12±0.22
R	0.9966	0.9873

 

For a more complete characterization, the data obtained were interpreted using the following rheological models: power law (figure 4), Cross (figure 5), Carreau (figure 6), Herschel-Bulkley (figure 7), Vocaldo (figure 8), and Casson (figure 9). It should be noted that in the mathematical expression of three models, namely Herschel-Bulkley, Casson and Vocaldo is found the flow effort τ_o.

The nonlinear regression method was used, using the Table Curve program. The Table Curve program allows the user to define a maximum of 50 nonlinear functions. A user-defined nonlinear function contains all the information needed to fit the function: the function name, the fitted parameters (constants), the function formula, the initial parameter estimates, the constraints for each parameter.

It is possible to graphically adjust the initial estimates to ensure better fit convergence. The model allows the introduction and adjustment of a maximum of 10 parameters, presented either as A, B, C, …, or in the form A0, A1, A2, …. The purpose of the graphical adjustment is to set the parameters in such a way that the start of fitting nonlinear to start with data closer to the values obtained. Partial derivatives of defined functions can be used to find insignificant parameters. If a partial derivative is constant, it must have the value 1, which means that it is a real constant (parameter) in the defined function. If a parameter has no significant contribution, this is a first indication that this parameter does not belong to the defined model.

The values of the rheological characteristics of the models used are those in table 2, and the curves calculated with the models used are presented graphically in figures 4-9.

Figure 4: Modeling of experimental data by nonlinear regression using the power law model for ruminal fluid obtained from feed with 40% barley (š), Click here to View figure

\

Figure 5: Modeling of experimental data by nonlinear regression using the Cross model for ruminal fluid obtained from feed with 40% barley (š) Click here to View figure

Figure 6. Modeling of experimental data by nonlinear regression using the Carreau model for ruminal fluid obtained from feed with 40% barley (š). Click here to View figure

Figure 7: Modeling of experimental data by nonlinear regression using the Herschel-Bulkley model for ruminal fluid obtained from feed with 40% barley (š). Click here to View figure

Figure 8: Modeling of experimental data by nonlinear regression using the Vocaldo model for ruminal fluid obtained from feed with 40% barley (š) Click here to View figure

Figure 9: Modeling of experimental data by nonlinear regression using the Casson model for ruminal fluid obtained from feed with 40% barley (š) Click here to View figure

It can be seen that the best overlaps between the experimental data and the calculated curves are obtained when using the Herschel-Bulkley, Casson and Vocaldo models, ie precisely the models that propose the existence of a flow effort. It appears from table 2 that for each of the two studied fluids, the flow effort has similar values, regardless of the rheological model used.

Table 2: The values of the rheological characteristics obtained by nonlinear regression from the rheological models used.

Models rheological	Rheological characteristics
	The classic diet	The classic diet with the addition of feed yeast
The law of power	K = 17.16 mPa . sn n = 0.470	K = 7.12 mPa . sn n = 0.436
Cross	ho = 28.3 mPa h∞ = 2.5 mPa k = 0.775 sn n = 1.106	ho = 688.4 mPa h∞ = 0.43 mPa k = 97.17 sn n = 0.677
Carreau	ho = 34.0 mPa k = 4.31 s s = 0.495	ho = 8.17 mPa k = 4.85 s s = 0.395
Herschel-Bulkley	ho = 8.5 mPa K = 9.5 mPa . sn n = 0.637	ho = 3.9 mPa K = 3.8 mPa . sn n = 0.605
Vocaldo	ho = 10.6 mPa k = 4.8 mPa-n . s n = 0.571	ho = 6.3 mPa k = 0.11 mPa-n . s n = 0.587
Casson	ho = 9.91 mPa k = 38.7 mPa . s-0.5	ho = 6.86 mPa k = 21.8 mPa . s-0.5

Conclusions

The following conclusions can be drawn from the experimental data. From the graphs it can be seen that the best overlaps between the experimental data and the calculated curves are obtained when using the Herschel-Bulkley, Casson and Vocaldo models, ie the models that propose the existence of a flow effort. It appears from table2 that for each of the two studied fluids, the flow effort has similar values, regardless of the rheological model used. The model that best describes the rheological behavior of sheep ruminal fluid is the model Herschel-Bulkley.

Conflict of Interest

There is no conflict of interest.

Funding Sources

There is no funding source.

References

1. Cretescu I., Drinceanu D., Mateescu C. T., Caprita R., & Chereji R.,  2009, Scientific Papers Animal Science and Biotechnologies, 42(1), 555-562.
2. Sari W. N., Safika D., & Fahrimal Y.,  2017, Veterinary world, 10(12), 1515.
   CrossRef
3. Okuskhanova E., Rebezov M., Yessimbekov Z., Tazeddinova D., Shcherbakov P., Bezhinar T., … & Stuart M., 2018,  Journal of Pharmaceutical Research International, 1-9.
4. Leng R. A., 2017, Animal Production Science, 57(11), 2188-2203.
   CrossRef
5. Adejoro F. A., Hassen A., & Thantsha M. S., 2018, PloS one, 13(10), e0206241.
   CrossRef
6. Bava L., Rapett L., Crovetto, G. M., Tamburini A., Sandrucci A., Galassi G., & Succi G., 2001, Journal of Dairy Science, 84(11), 2450-2459.
   CrossRef
7. Creţescu I. 2006, Cercetări asupra mecanicii fluidelor la nivelul tubului ndigestiv la rumegătorii mici, Teză doctorat, USAMVB Timişoara
8. Cretescu I., Mateescu C., Caprita R., Drinceanu D., 2006. Rheological Characteristics of the Ruminat Fluid of the small Ruminants Feeded with Different Ratia of Barley, Lucrari Stiintifice, ser. Zootehnie, 49, 432-437
9. Cretescu I., Drinceanu D., Caprita R., Mateescu C., Chereji R., 2005, YEA SACC1026 influence on some biophysical parameters of the ruminal fluid. Lucrari Stiintifice. Zootehnie si Biotehnologii Animaliere (Republica Moldova), 13, 315-317
10. Hurtaud C., & Peyraud J. L., 2007, Journal of Dairy Science, 90(11), 5134-5145.
    CrossRef
11. Ahmed J., Al-Salman F., & Almusallam A. S., 2013,  Journal of Food Engineering, 119(3), 660-667.
    CrossRef
12. Stanciu I., 2014, International Research Journal of Pure and Applied Chemistry, 531-540.
    CrossRef
13. Stanciu I., 2013, Journal of Science and Arts, 13(4), 355.
    CrossRef
14. Barnes H. A., 2000, A handbook of elementary rheology, Institute of Non-Newtonian Fluid Mechanics, Aberystwyth, UK.
15. Stanciu I., 2018, Journal of Science and Arts, 3(44), 711-716.
16. Stanciu I., 2019, Journal of Science and Arts,3(48), 703-708.
17. Stanciu I., 2019, Journal of Science and Arts, 4(49), 938-988.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.