Influence of Temperature on the Rheological Behavior of Non-Additive Olive Oil

Introduction

Flow is a continuous deformation of the fluid that occurs when the resultant of the forces acting on the fluid is non-zero. Historically, the classical theory of fluid dynamics has developed through theoretical studies by Pascal (in 1663), Bernoulli (in 1738) and Euler (in 1755) on a viscous fluid – the ideal fluid or Pascal’s fluid. Pascal’s fluid is a fluid that flows even if the shear stress is zero. This fluid is without viscosity, being an ideal fluid that cannot be found among real fluids. Ideal fluids (without viscosity) or Pascal fluids are therefore homogeneous media without viscosity, ie they do not resist deformation ^1-4.

Practice has refuted the results based on the ideal fluid model. Thus, it was found that in reality the energy consumption required for the transport or mixing of fluids is higher than that calculated in the ideal fluid hypothesis. In the first part of the twentieth century, Ludwig Prandtl tried to overcome the shortcomings of theories based on the non-viscosity fluid model by introducing the concept of hydrodynamic boundary layer.

According to this theory, at the interface between a fluid and a solid surface an area is formed in which the interactions between the fluid and the solid are manifested as resistance forces that oppose the flow. Outside the boundary layer, the flow is devoid of internal resistances, leaving the flow equations of the ideal fluids valid. Real fluids are those fluids that resist deformation and rise, due to the frictional forces between the layers. The intensity of these forces is expressed by the dynamic viscosity of the fluids, thus being able to conclude that the real fluids have viscosity ^5-9.

For many fluids the viscosity depends only on the state parameters (temperature and pressure) and does not depend on the parameters of the stresses to which the fluid is subjected (shear stress and shear rate). These fluids are called Newtonian fluids. Development of new industries such as: rubber industry, plastic molds, synthetic fibers, etc. pointed out that there are also fluids whose viscosity is dependent on the parameters of the stresses and sometimes on time. These real fluids have been called non-Newtonian fluids.

The rheological behavior of food fluids depends on their composition and temperature. Their flow behavior also depends on the shear rate, shear duration and pre-shear history ⁴. For a more complete rheological characterization of a food fluid, it is usual to record the rheograms of these fluids. Rheograms express the dependence of the (tangential) shear stress on the shear rate, τ = ƒ(γ). After the recording of the rheograms follows a delicate stage, namely their interpretation ^10-14.

With the increase of the deformation speed, ie the shear rate, the constituent particles are oriented in the direction of flow. Molecular chains in melts or solutions unfold, stretch, and orient in parallel with the direction of action of the forces that tend to deform the fluid domain. This orientation allows the relative sliding between the fluid layers, corresponding to a reduction of the viscosity. Deformation can cause disaggregation of particle agglomerations, having the effect of accelerating the flow, thus reducing the viscosity. For most fluids, the pseudoplast behavior is reversible, with a certain delay, so the viscosity increases with the decrease of the deformation rate and the disordered orientation of the constituent particles is restored, due to Brownian agitation.

In other words, the nonlinear mechanical properties of these fluids are attributed to changes that occur in the organization of the component molecules of the fluid, when they are subjected to a force that induces the deformation of the fluid. In the case of small molecules and molecular segment rotations, the duration of these changes is of the order of 10^-12 s to 10^-9 s being equivalent to the duration of Brownian fast motions. In the case of slow movements of reorientation or reorganization of macromolecules or large groups of molecules, the duration is longer, being of the order of 10^-3 – 10⁰ s.

A number of liquid fluids exhibit pseudoplastic flow behavior. In most cases, this non-Newtonian behavior can be attributed to either the presence in solution of high molecular weight substances or solids dispersed in the fluid phase. Depending on their size and concentration, solid particles may remain suspended in solution or, under the action of gravity, may settle^14-17

Material and methods

The olive oil purchased from the manufacturer was studied on the entire range of shear speeds in the temperature range 40-100^oC with the Haake VT 550 viscometer with VH₁ sensor. Experiments were performed in two main categories to explore changes in viscosity based on temperature and shear rate.

Results and discussion

Figures 1-7 show the dependence of the dynamic viscosity on the shear rate at all temperatures at which the sample of non-additive olive oil was studied.

The shear experiment shows an almost Newtonian response to olive oil, especially at higher shear rates. In Figure 1 to Figure 7 the viscosities are plotted for different temperatures depending on the shear rate. Here, the readings of low shear values ​​may not be very accurate due to the restriction of the equipment to high temperatures. Therefore, some curves in the figures require additional effort to further validate the results. Therefore, the shear rate of the temperature experiment was set at the rate of 120 s^-1. Also note that with increasing temperature, olive oil exhibits a certain thin shear behavior at low shear rates. The heels developed due to the shear stress in the samples at both high temperatures and low shear rates are small and therefore more difficult to indicate by rheometer. However, it is obvious from the figure that there is a thinning of the cut. For olive oil, Figure 1 shows that, beyond the shear rates of 10.6 s^-1, the oil is essentially Newtonian at all temperatures.

Figure 1: The correlation  dynamic viscosity on the shear rate  at temperature of  400C for right to B and 1B represents the exponential fitting to B Click here to View figure

Figure 2: The correlation  dynamic viscosity on the shear rate  at temperature of  500C for right to C and 1C represents the exponential fitting to C Click here to View figure

Figure 3: The correlation  dynamic viscosity on the shear rate  at temperature of  600C for right to D and 1D represents the exponential fitting to D Click here to View figure

Figure 4: The correlation  dynamic viscosity on the shear rate  at temperature of  700C for right to E and 1E represents the exponential fitting to E Click here to View figure

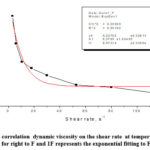Figure 5: The correlation  dynamic viscosity on the shear rate  at temperature of  800C  for right to F and 1F represents the exponential fitting to F Click here to View figure

Figure 6: The correlation  dynamic viscosity on the shear rate  at temperature of  900C for right to G and 1G represents the exponential fitting to G Click here to View figure

Figure 7: The correlation  dynamic viscosity on the shear rate  at temperature of  1000C for right to H and 1H represents the exponential fitting to H Click here to View figure

Conclusion

The rheology of olive oil at different temperatures and shear rates has been studied. At low temperatures it has a thickening effect and at high temperatures a thin oil film subjected to different shear rates. It has a non-Newtonian behavior at all temperatures at which it was studied. Over time, olive oil has the effects of thinning the temperature to lower temperatures, they become thickened at the temperature as they are heated above a critical temperature. Olive oil exhibits Newtonian behavior at a wide range of shear rates. As no time effect was observed, thixotropy was not a concern. The temperature-dependent viscosity of olive oils can be attributed to microstructural changes in the samples. It can be concluded that high temperatures, together with shear stress, lead to unsaturation of olive oils, manifested by a decrease in viscosity to a critical temperature beyond which the viscosity increases. This (high) temperature thickening involves a change in the microstructure, making some olive oils unsuitable for frying. A statement that requires more research to prove for sure.

Conflict of Interest

There is no conflict of interest.

Funding Sources

None

References

1. Rao M. A., 1977,  J. Tex- ture Studies,8, 135.
   CrossRef
2. Goodrum J. W., Eitman M. A., 1996, Bioresources Technology, 56, 55.
   CrossRef
3. Geller D. P., Goodrum J. W., 2000, J. American Oil Chemist’s Society , 77, 111.
   CrossRef
4. Koliandris A. L., Rondeau E., Hewson L., Hort J., Tay- lor A. J., Cooper-White J., Wolf B., 2011,  Appl. Rheol., 21, 13777.
5. Santos J. C.O., Santos I. M. G., Conceicao M. M., Porto S. L. , Trindade M. F. S., Souza A. G., Prasad S., Fernandes V. J., Araujo A. S., 2004, J. Thermal Analysis and Calorimetry, 75, 419.
   CrossRef
6. Stanciu I.,  2018,  Journal of Science and Arts, 18(2), 453-458.
7. Venerus D. C., Buongiorno J., Christianson R., Townsend J., Bang I., Chen G., Chung S., Chyu M., Chen H., Ding Y., Dubois F., Dzido G., Funfschilling D., Galand Q., Gao J., Hong H., Horton M., Hu L-W., Iorio C. S., Jarzebski A. B., Jiang Y., Kabelac S., Kedzier- ski M. A., Kim C., Kim J-H., Kim S., McKrell T., Ni R., Philip J., Prabhat N., Song P., VanVaerenbergh S., Wen D., Witharana S., Zhao X-Z., Zhou S-Q, 2010, Appl. Rheol. 20, 44582.
8. Angerosa F., Mostallino R., Basti C., Vito R., 2001, Food Chemistry, 72, 19.
   CrossRef
9. Stanciu I., 2011, J. Sci. Arts, 1, 55-58.
10. Santos J. C. O., Santos I. M. G., Souza A. G., 2005,  J. Food Eng., 67, 401.
    CrossRef
11. Sanchez-Gimeno A. C., Negueruela A. I., Benito M., Vercet A., Oria R., 2008, Food Chemistry, 110, 654.
    CrossRef
12. Stanciu I., 2014, International Research Journal of Pure and Applied Chemistry, 531-540.
    CrossRef
13. Stanciu I., 2013, Journal of Science and Arts, 13(4), 355.
    CrossRef
14. Barnes H. A., 2000, A handbook of elementary rheology, Institute of Non-Newtonian Fluid Mechanics, Aberystwyth, UK.
15. Stanciu I., 2018, Journal of Science and Arts, 3(44), 711-716.
16. Stanciu I., 2019, Journal of Science and Arts, 3(48), 703-708.
17. Stanciu I., 2019, Journal of Science and Arts, 4(49), 938-988.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.